Numpy的21个常用知识点

前言

有些萌新还在使用Pycharm进行Numpy等的学习，个人建议不要偷懒，下载anaconda，使用Jupyter Notebook进行探索性学习。不明白他们之间关系的可以看以下文章。

https://blog.csdn.net/suic009/article/details/122803865?spm=1001.2014.3001.5502

当我们在Jupyter Notebook中执行import numpy未发生报错时，说明下载成功。

不成功的记得在编译器中pip install numpy 或者conda install numpy，注意环境变量和下载位置。

当然也可以查看其版本：

(小白ps：as的作用是给其起个别名；__version__，这样形式的一般都是使用的这个类或者对象内部的一些属性方法如__name__、__sizeof__()等。) 

Jupyter提词器下载：

提前退出anaconda，打开anaconda prompt输入以下命令： 

pip install jupyter_contrib_nbextensions -i https://pypi.mirrors.ustc.edu.cn/simple
jupyter contrib nbextension install --user

pip install --user jupyter_nbextensions_configurator 
jupyter nbextensions_configurator enable --user

再次进入jupyter notebook多了以下选项，点击进入 

取消勾选，选中Hinterland

 成功

一、Numpy与Python用于数组计算的性能对比

首先我们以一个需求进行分析：

• 数组A是1~N数字的平方
• 数组B是1~N数字的立方
• 实现两个数组的加法

对比使用Numpy和原生Python的性能对比

对于Python：

def python_sum(n):
    """ Python实现数组的加法
    @param n：数组的长度
    """
    a = [i**2 for i in range(n)] # 生成第一个数组
    b = [i**3 for i in range(n)] # 生成第二个数组
    c = []
    for i in range(n):
        c.append(a[i] + b[i])
    return c

对于使用Numpy：

def numpy_sum(n):
    """ numpy实现数组的加法
    @param n：数组的长度
    """
    a = np.arange(n) ** 2 # 0 - n-1 每个数平方
    b = np.arange(n) ** 3
    return a+b # 结果元素与上方python相同。

我们分别对python_sum和numpy_sum传入1K，1W，10W、100W、1000W次对比运行时间：

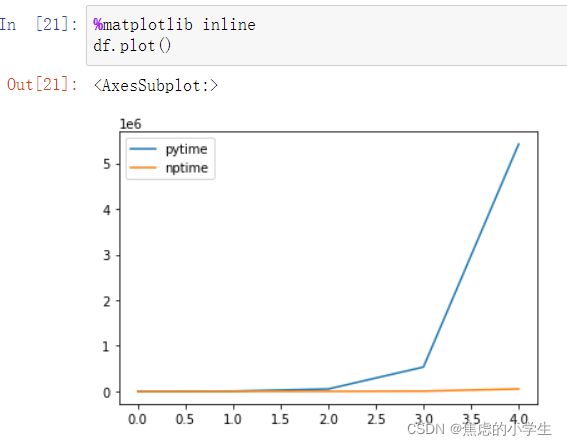
%timeit python_sum(n)

%timeit numpy_sum(n)

将结果打包在一起，得到如下(记得统一时间单位，这里统一微秒。)：

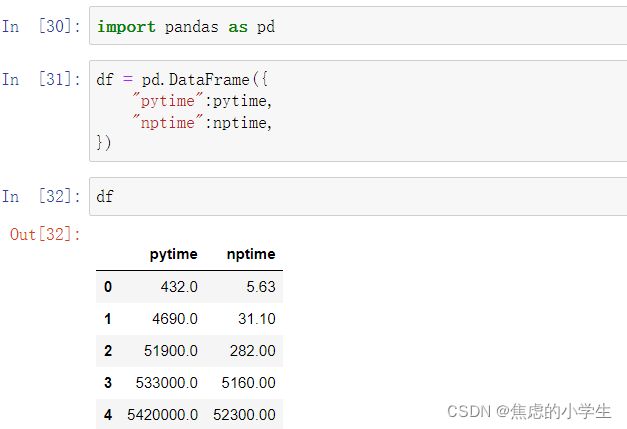
pytime = [432,4.69*1000,51.9*1000,533*1000,5.42*1000*1000]
nptime = [5.63,31.1,282,5.16*1000,52.3*1000]

我们引用后面学到的Pandas将其转变为DataFrame形式的二维表格：

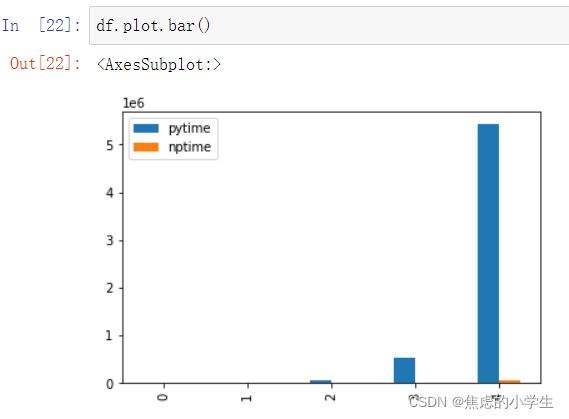
此时我们得到df。使用后面学到的matplotlib进行画图：

或

至于其为什么这么高效，除了内部的一些优化操作更加便捷以外，其数据类型更接近C语言。如Python中一个int类型占28个字节(24个来自于int封装对象，4个字节来自真正的int)，而在numpy中一个int类型默认只占4字节。

anaconda中还有很多强大的功能，这些都离不开C语言，我们可以看到在ananconda的安装目录有存有MinGW文件。

二、Numpy的核心array

array对象的背景：

• Numpy的核心数据结构，就叫做array就是数组，array对象可以是一维数组，也可以是多维数组；
• Python的List也可以实现相同的功能，但是array比List的优点在于性能好、包含数组元数据信息、大量的便捷函数；
• Numpy成为Scipy、Pandas、Scikit-Learn、Tensorflow、PaddlePaddle等框架的“通用底层语言”
• Numpy的array和Python的List的一个区别，是它元素必须都是同一种数据类型，比如都是数字int类型，这也是Numpy高性能的一个原因；

array本身的属性

• shape：返回一个元组，表示array的维度
• ndim：一个数字，表示array的维度的数目
• size：一个数字，表示array中所有数据元素的数目
• dtype：array中元素的数据类型

创建array的方法

• 从Python的列表List和嵌套列表创建array
• 使用预定函数arange、ones/ones_like、zeros/zeros_like、empty/empty_like、full/full_like、eye等函数创建
• 生成随机数的np.random模块构建

array本身支持的大量操作和函数

• 直接逐元素的加减乘除等算数操作
• 更好用的面向多维的数组索引
• 求sum/mean等聚合函数
• 线性代数函数，比如求解逆矩阵、求解方程组

2.1 使用list创建一维array和二维array

2.2 数组array的属性

Array.shape 查看数组的形状

Array.ndim 查看数组的维度

Array.size 查看数组中元素的个数

Array.dtype 查看数组中元素的类型

Array.itemsize 查看单个元素所占字节数

Array.nbytes 查看数组中所有元素所占字节数

再次提醒，为保证高效率的计算，数组中的元素会统一类型。

如arr = [1,2.0,'3'] 元素类型会全部转变为object字符类型。没有object的话其次才是浮点型。

2.3 常用的array生成函数

以下除了arrange和random，基本都是xx:生成xx类型数组；xx_like(a)模仿数组a生成xx类型数组。

使用arange创建数字序列

arange([start,] stop[, step,], dtype=None)

使用ones创建全是1的数组

np.ones(shape, dtype=None, order='C')

shape : int or tuple of ints
Shape of the new array, e.g., ``(2, 3)`` or ``2``.

使用ones_like创建形状相同的数组

ones_like(a, dtype=float, order='C')

使用zeros创建全是0的数组
np.zeros(shape, dtype=None, order='C')

使用zeros_like创建形状相同的数组
np.zeros_like(a, dtype=None)

使用empty创建全是0的数组
empty(shape, dtype=float, order='C')   
注意：数据是未初始化的，里面的值可能是随机值不要用

使用empty_like创建形状相同的数组
empty_like(prototype, dtype=None) 

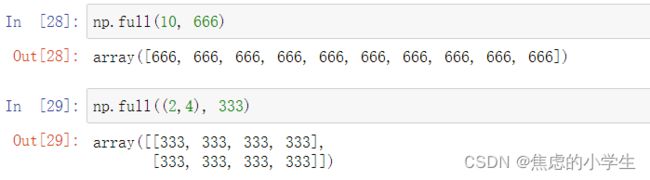
使用full创建指定值的数组
np.full(shape, fill_value, dtype=None, order='C')

使用full_like创建形状相同的数组
np.full_like(a, fill_value, dtype=None) 

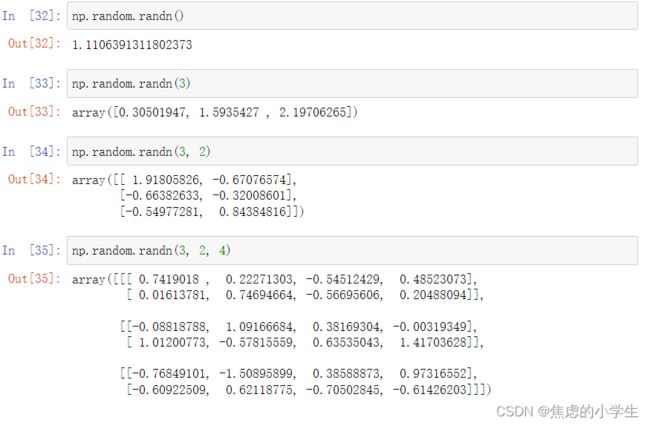
使用random模块生成随机数的数组

randn(d0, d1, ..., dn) 随机数会在后面讲解

2.4 array本身支持大量操作和函数

这里先稍做展示，后面会经常用到。 

比如这样生成一个二维数组：

运算：

三、给数组排序

Numpy给数组排序的三个方法：  

• numpy.sort：返回排序后数组的拷贝，即不改变本身。
• array.sort：原地排序数组而不是返回拷贝，即改变本身。
• numpy.argsort：间接排序，返回的是排序后的数字索引

3个方法都支持一个参数kind，可以是以下一个值：

• quicksort：快速排序，平均O(nlogn)，不稳定情况
• mergesort：归并排序，平均O(nlogn)，稳定排序
• heapsort：堆排序，平均O(nlogn)，不稳定排序
• stable：稳定排序

3.1 np.sort排序

3.2 array.sort排序 

即np.sort不改变操作的数组返回一个新数组，array.sort改变操作的数组。

个人喜欢用np.sort()，就算需要改变数组本身时，直接以arr = np.sort(arr)这种形式写就行了，要会灵活运用。

3.3  np.argsort 返回的是有序数字的索引

3.4 Python原生sorted与np.sort对比 

首先我们都知道python的列表里有一个.sort方法，这个方法是list独有的且也只能操作list。对于list.sort()它没有返回值改变list本身，要求内部类型统一否则会报错。

对于sorted(list)它的局限反而没那么大，还可以对字典等根据某个键、值进行排序。

但这些排序的内部都是基于冒泡排序完成的。而我们的np.sort则是快速排序。

由于快速排序具有很强的不稳定性， 所以也有上面说的这些可选：

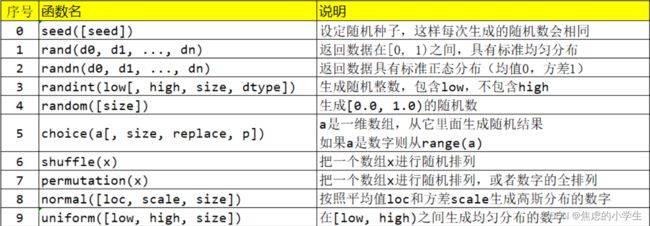
四、Numpy常用random函数

常用如下： 

更多请查看官方网址：https://docs.scipy.org/doc/numpy-1.14.0/reference/routines.random.html 

1. rand(d0, d1, ..., dn)

返回数据在[0, 1)之间，具有均匀分布

2. randn(d0, d1, ..., dn)

返回数据具有标准正态分布（均值0，方差1）

3. randint(low[, high, size, dtype])

生成随机整数，包含low，不包含high  
如果high不指定，则从[0, low)中生成数字

(ps：在python中random.randint(a,b) 是包含b的）

4. random([size])    

生成[0.0, 1.0)的随机数

5. choice(a[, size, replace, p])

a是一维数组，从它里面生成随机结果

6. shuffle(x)     

把一个数组x进行随机排列

7. permutation(x)

把一个数组x进行随机排列，或者数字的全排列

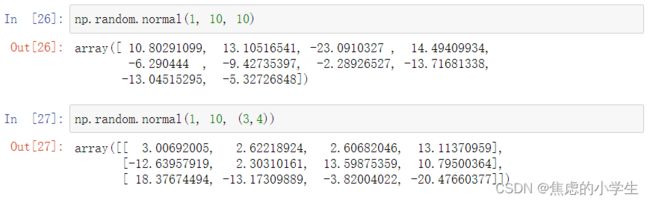
8. normal([loc, scale, size])

按照平均值loc和方差scale生成高斯分布的数字

9. uniform([low, high, size]) 

在[low, high)之间生成均匀分布的数字

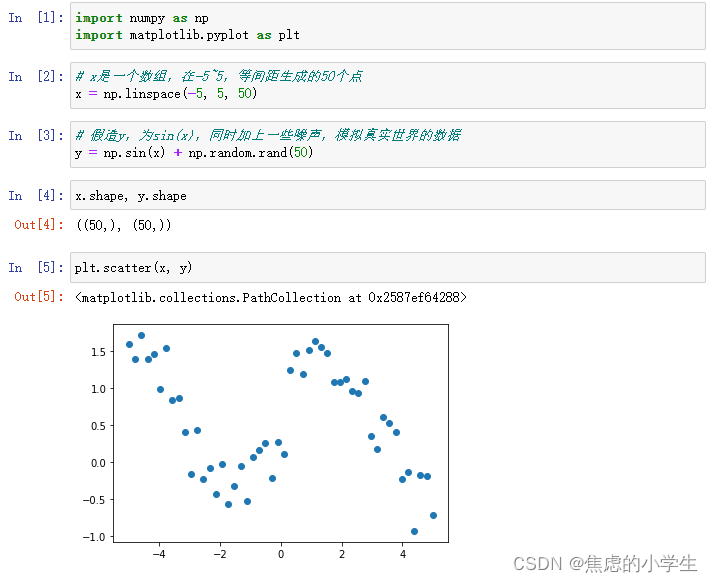
实例：对数组加入随机噪声

五、Numpy对数组按索引查询

三种索引方法：

• 基础索引
• 神奇索引
• 布尔索引

5.1 基础索引

对于一维数组，和list一样，这里略。

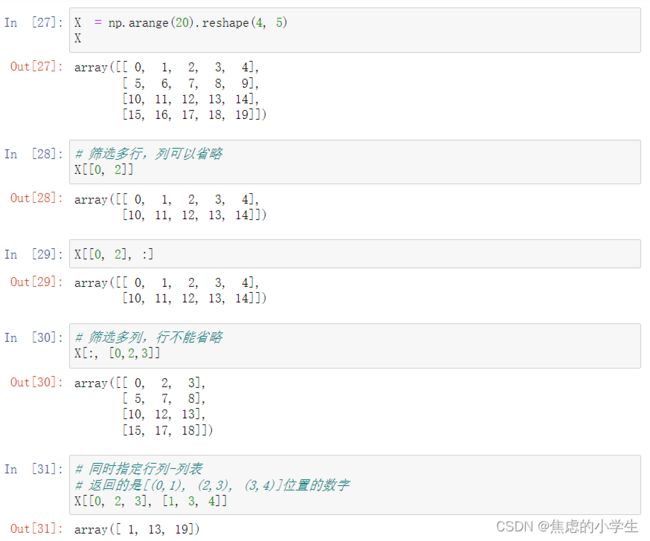
对于二维数组，我们用行坐标和列坐标进行定位：

X[行,列]  其中行列可以是数字坐标，也可以是类似切片类型的数据。列可以不写，此时只对行操作。

与列相关： 

我们可以取切片进行多个数据的修改：

5.2 神奇索引 

我们前面用数字当索引，其实也可以用数组。

数字索引返回单个数据，数字切片索引返回从哪到哪的数据。而神奇索引返回数组对应下几个的值。

实例：获取数组中最大的前N个数字 

对于二维数组，原理相同： 

5.3 布尔索引

根据True或False返回对应的数据。

对于二维：

还可以使用一些条件组合：

六、Numpy中的数学统计函数

1、Numpy有哪些数学函数： 

函数名	说明
np.sum	所有元素的和
np.prod	所有元素的乘积
np.cumsum	元素的累积加和
np.cumprod	元素的累积乘积
np.min	最小值
np.max	最大值
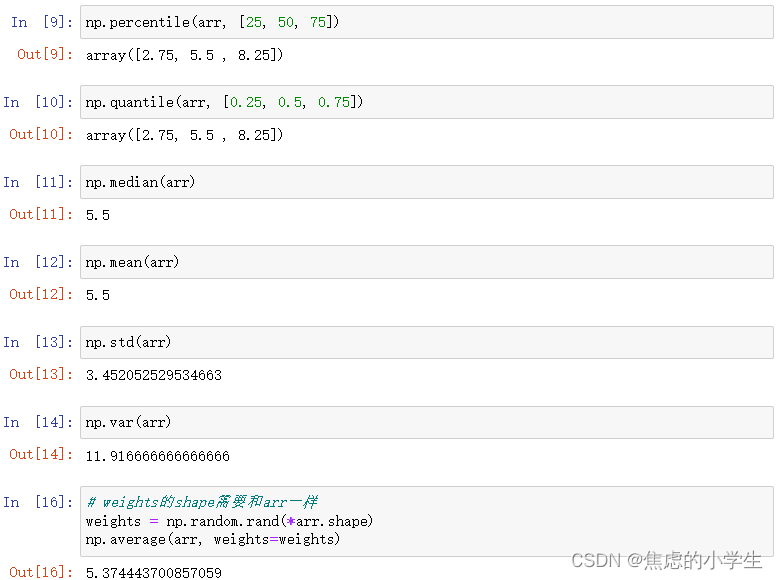
np.percentile	0-100百分位数
np.quantile	0-1分位数
np.median	中位数
np.average	加权平均，参数可以指定weights
np.mean	平均值
np.std	标准差
np.var	方差

2、怎样实现按不同的axis计算

以上函数，都有一个参数叫做axis用于指定计算轴为行还是列，如果不指定，那么会计算所有元素的结果

3、实例：机器学习将数据进行标准化

A = (A - mean(A, axis=0)) / std(A, axis=0)

6.1 Numpy中的数学统计函数

6.2 Numpy的axis参数用途 

6.3 机器学习将数据标准化

 

七、Numpy计算数组中满足条件的个数

需求：有一个非常大的数组比如1亿个数字，求出里面数字小于5000的数字数目

 1. 使用numpy的random模块生成1亿个数字

2. 使用Python原生语法实现

3. 使用Numpy向量化操作实现 

4. 时间对比

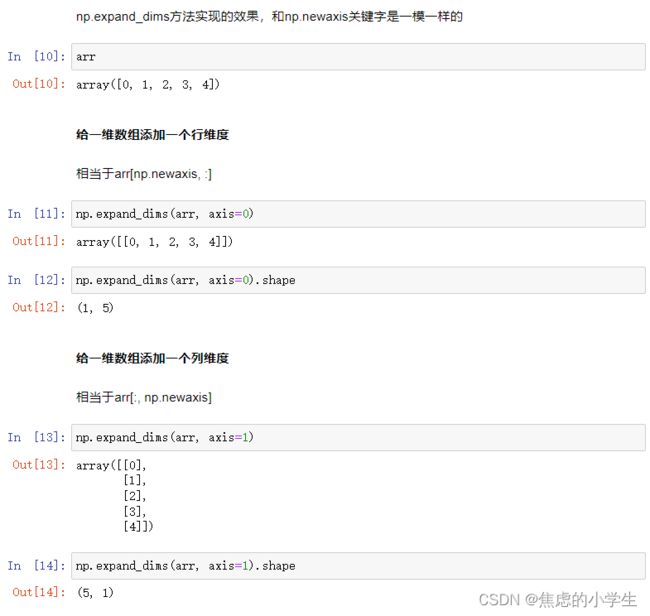
八、给数组增加维度的三种方法

背景：
很多数据计算都是二维或三维的，对于一维的数据输入为了形状匹配，经常需升维变成二维

需要： 
在不改变数据的情况下，添加数组维度；（注意观察这个例子，维度变了，但数据不变）  
原始数组：一维数组arr=[1,2,3,4]，其shape是(4, )，取值分别为arr[0],arr[1],arr[2],arr[3]  
变形数组：二维数组arr[[1,2,3,4]]，其shape实(1,4), 取值分别为a[0,0],a[0,1],a[0,2],a[0,3]

实操：
经常需要在纸上手绘数组的形状，来查看不同数组是否形状匹配，是否需要升维降维

3种方法：

• np.newaxis：关键字，使用索引的语法给数组添加维度
• np.expand_dims(arr, axis)：方法，和np.newaxis实现一样的功能，给arr在axis位置添加维度
• np.reshape(a, newshape)：方法，给一个维度设置为1完成升维

方法1：np.newaxis关键字 

方法2 ：np.expand_dims方法

方法3：np.reshape方法

九、Numpy实现K折交叉验证的数据划分

背景：K折交叉验证

为什么需要这个？
在机器学习中，因为如下原因，使用K折交叉验证能更好评估模型效果：
1. 样本量不充足，划分了训练集和测试集后，训练数据更少；
2. 训练集和测试集的不同划分，可能会导致不同的模型性能结果；

K折验证是什么 
K折验证（K-fold validtion）将数据划分为大小相同的K个分区。  
对每个分区i，在剩余的K-1个分区上训练模型，然后在分区i上评估模型。  
最终分数等于K个分数的平均值，使用平均值来消除训练集和测试集的划分影响；

1. 模拟构造样本集合

2. 使用Numpy实现K次划分

结果如下：

十、Numpy数组合并操作

背景：在给机器学习准备数据的过程中，经常需要进行不同来源的数据合并的操作。

两类场景：
1. 给已有的数据添加多行，比如增添一些样本数据进去；
2. 给已有的数据添加多列，比如增添一些特征进去；

以下操作均可以实现数组合并：

• np.concatenate(array_list, axis=0/1）：沿着指定axis进行数组的合并
• np.vstack或者np.row_stack(array_list)：垂直vertically、按行row wise进行数据合并
• np.hstack或者np.column_stack(array_list)：水平horizontally、按列column wise进行数据合并

1. 添加多行 

2. 添加多列

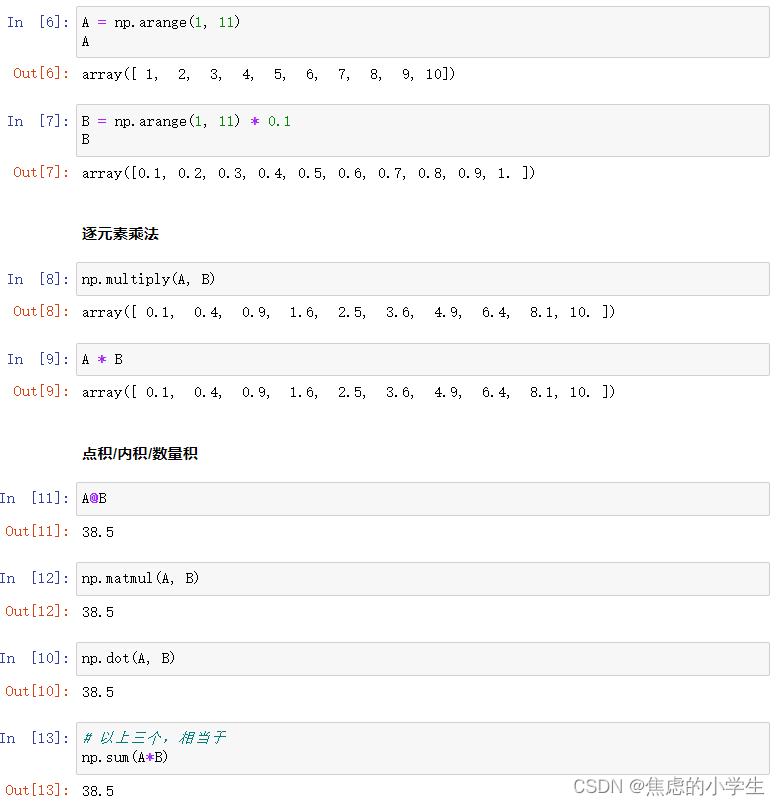
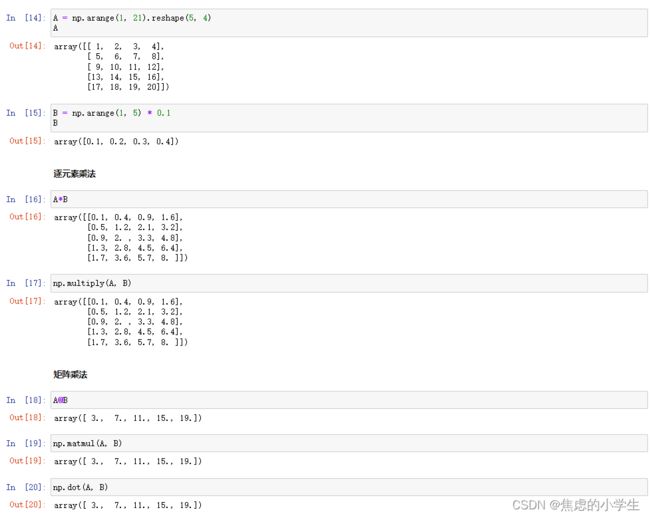
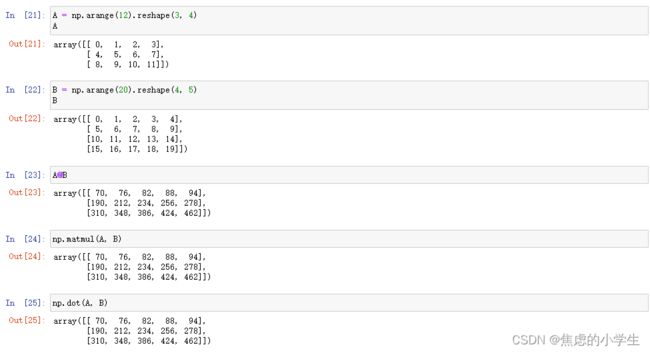
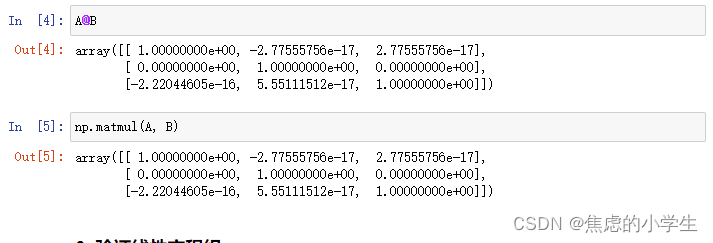
十一、数组的乘法

按照两个相乘数组A和B的维度不同，分为以下乘法：

1. 数字与一维/二维数组相乘；
2. 一维数组与一维数组相乘；
3. 二维数组与一维数组相乘；
4. 二维数组与二维数组相乘；

numpy有以下乘法函数： 

1. *符号或者np.multiply：逐元素乘法，对应位置的元素相乘，要求shape相同
2. @符号或者np.matmul：矩阵乘法，形状要求满足(n,k),(k,m)->(n,m)
3. np.dot：点积乘法

解释：点积，也叫内积，也叫数量积
两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：   
a·b=a1b1+a2b2+……+anbn。

1. 数字与数组相乘

2. 一维数组与一维数组相乘

3 . 二维数组和一维数组相乘

4. 二维数组与二维数组相乘

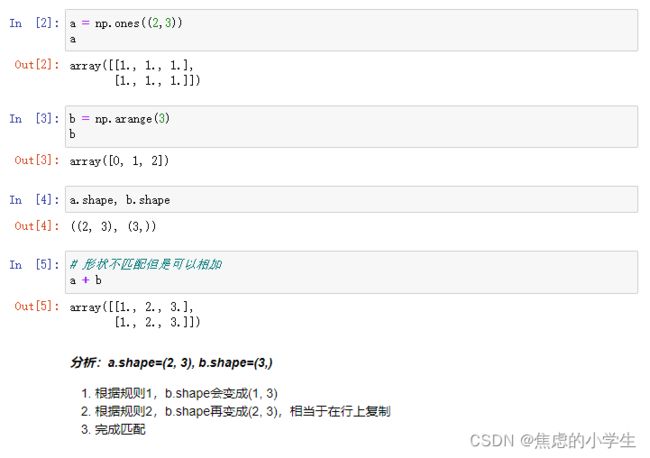
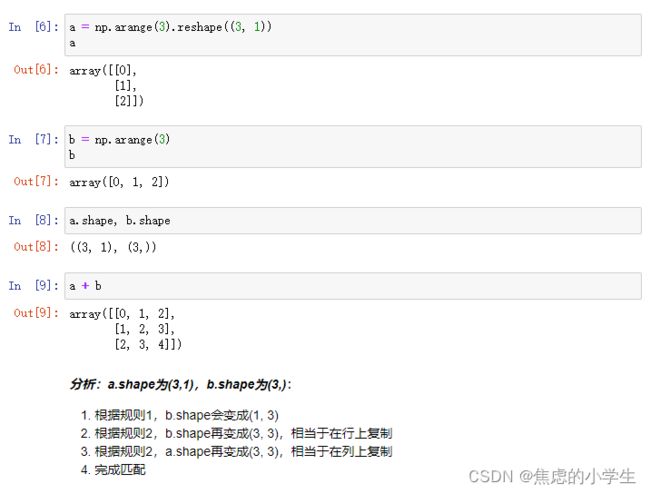
十二、Numpy中广播的概念

广播：
简单理解为用于不同大小数组的二元通用函数（加、减、乘等）的一组规则

广播的规则：
1. 如果两个数组的维度数dim不相同，那么小维度数组的形状将会在左边补1
2. 如果shape的维度不匹配，但是有维度是1，那么可以扩展维度是1的维度匹配另一个数组；
3. 如果shape的维度不匹配，但是没有任何一个维度是1，则匹配失败引发错误；

1. 二维数组加一维数组

2 .两个数组均需要广播

3. 不匹配的例子 

十三、Numpy求解线性方程组

对于Ax=b，已知A和b，怎么算出x?

求解： 

验证：

十四、Numpy实现SVD矩阵分解

从分量还原矩阵 

十五、Numpy实现多项式曲线拟合

问题定义：  
对于一堆数据点(x, y)，能否只根据这些数据，找出一个函数，使得函数画出来的曲线和原始数据曲线尽量匹配？

多项式拟合问题：   
任何可微连续的函数，都可以用一个N次多项式来估计，而比N次幂更高阶的部分为无穷小可以忽略不计

3次多项式即：a$x^3$ + b$x^2$ + cx + d  
比如我们可以让sin(x) 约等于 a$x^3$ + b$x^2$ + cx + d

1. 构造原始数据

2. 使用Numpy拟合

十六、使用Matplotlib实现可视化绘图

 可以直接将Numpy的数组传给Matplotlib实现可视化绘图：  

• 曲线图
• 饼图
• 柱状图
• 直方图

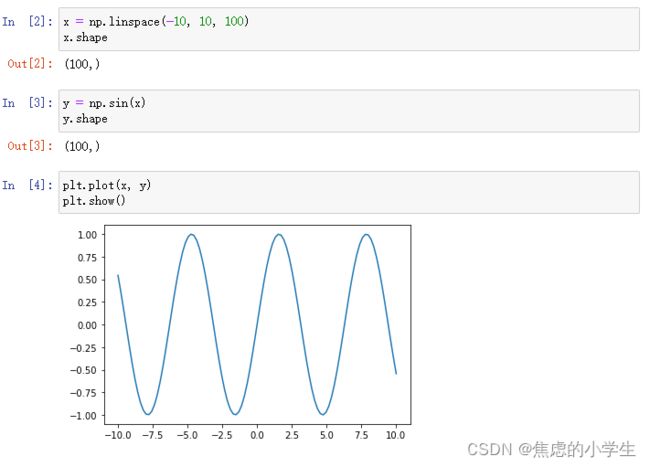
1. 绘制正弦曲线

2. 绘制饼图

3. 柱状图 

4. 直方图

十七、Numpy实现逆矩阵求解线性方程组

对于这样的线性方程组：

• x + y + z = 6
• 2y + 5z = -4
• 2x + 5y - z = 27

可以表示成矩阵的形式：

用公式可以表示为：Ax=b，其中A是矩阵，x和b都是列向量

逆矩阵（inverse matrix）的定义：  
设A是数域上的一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，则我们称B是A的逆矩阵，而A则被称为可逆矩阵。注：E为单位矩阵。

使用逆矩阵求解线性方程组的方法：
两边都乘以$A^{-1}$，变成$A^{-1}$Ax=$A^{-1}$b，因为任何矩阵乘以单位矩阵都是自身，所以x=$A^{-1}$b

1. 求解逆矩阵

2. 验证矩阵和逆矩阵的乘积是单位矩阵 

3. 验证线性方程组

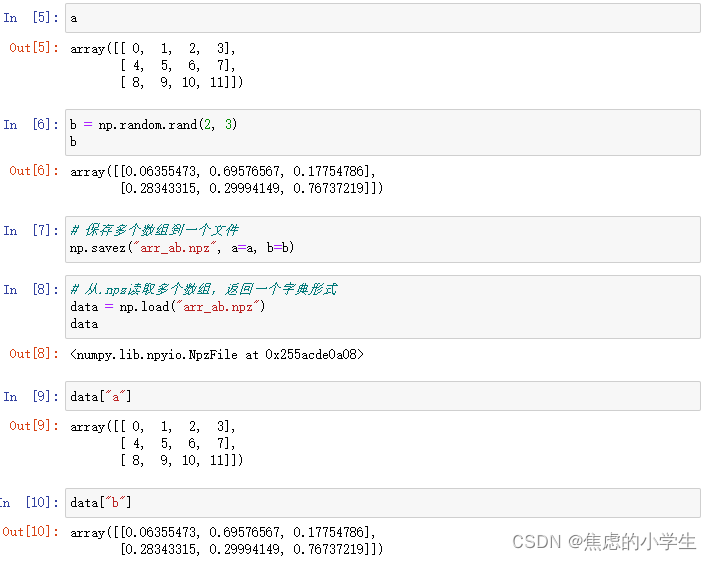
十八、Numpy将数组写到文件

## Numpy怎样将数组读写到文件

本文档介绍的是Numpy以自己内建二进制的方式，将数组写出到文件，以及从文件加载数组；

如果是文本、表格类数据，一般使用pandas这个类库做加载和处理，不用numpy

几个方法：
1. np.load(filename)：从.npy或者.npz文件中加载numpy数组  
如果文件后缀是.npy返回单个数组，如果文件后缀是.npz返回多个数组的字典
2. np.save(filename, arr)：将单个numpy数组保存到.npy文件中
3. np.savez(filename, arra=arra, arrb=arrb)：将多个numpy数组保存到.npz未压缩的文件格式中
4. np.savez_compressed(filename, arra=arra, arrb=arrb)：将多个numpy数组保存到.npz压缩的文件格式中

.npy和.npz都是二进制格式文件，用纯文本编辑器打开都是乱码

1. 使用np.save和np.load保存和加载单个数组

2. 使用np.savez和np.load保存和加载多个数组

3. 使用np.savez_compressed和np.load保存和加载多个数组到压缩格式文件

十九、Numpy的结构化数组

一般情况下，Numpy中的数组都是同样的数据类型，比如int、float；  
这也是Numpy性能高效的原因，在内存中紧凑存储，读取非常快；  

但是Numpy也可以记录异构数组，比如下面的数据：

姓名	年龄	体重
小王	30	80.5
小李	28	70.3
小天	29	78.6

1. 正常的Numpy数组的dtype值只有一个类型

2. 怎样使用Numpy表达异构数据

3. 针对异构数组的查询和操作

使用列表的方式查询一行

使用字典的方式查询一列

按条件查询

对单列做逐元素计算

最后的一言：  
* 对于这种每列类型不同的“异构数据”，Pandas更擅长处理；
* 但我们还要学习一下Numpy结构化数组，不一定会使用它，但要能读懂别人的代码

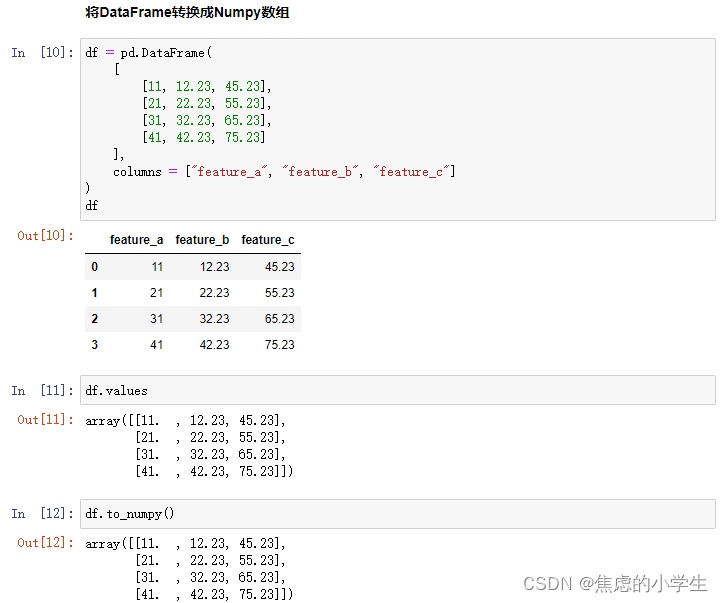
二十、Numpy与Pandas数据的相互转换

Pandas是在Numpy基础上建立的非常流行的数据分析类库；  
提供了强大针对异构、表格类型数据的处理与分析能力。

本次介绍Numpy和Pandas的转换方法：  

• Numpy数组怎样输入给Pandas的Series、DataFrame；
• Pandas的Series、DataFrame怎样转换成Numpy的数组

将Numpy数组转换成Pandas的数据结构 

 

将Pandas的数据结构转换成Numpy数组

* 方法1：.values()
* 方法2：.to_numpy()

用途：  
比如Scikit-Learn的模型输入需要的是Numpy的数组  
可以使用Pandas对原始数据做大量的处理后，将结果数据转换成Numpy数组作为输入

 

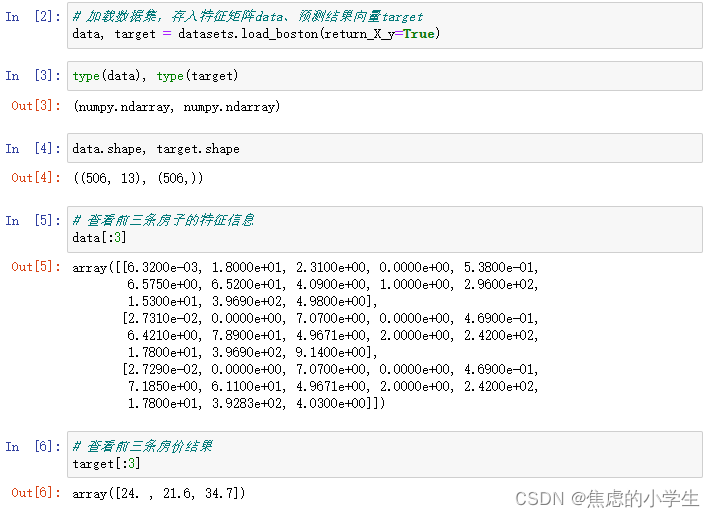
二十一、Numpy数据输入给Sklearn实现模型训练

Numpy的数组怎样与sklearn模型交互，包括训练测试集拆分、输入给模型、评估模型、模型预估对于大家自己的任务，可以提前处理成这样的Numpy格式，然后输入给sklearn模型

import numpy as np
# 使用sklearn自带的数据集，这些数据集都是Numpy的形式
# 我们自己的数据，也可以处理成这种格式，然后就可以输入给模型
from sklearn import datasets
# 用train_test_split可以拆分训练集和测试集
from sklearn.model_selection import train_test_split
# 使用LinearRegression训练线性回归模型
from sklearn.linear_model import LinearRegression

1. 加载波斯顿房价数据集

2. 拆分训练集和测试集

3. 训练线性回归模型

4. 评估模型和使用模型