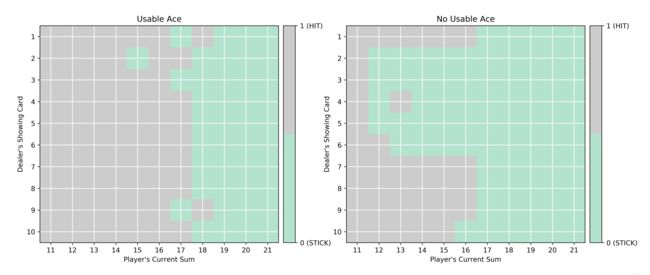
蒙特卡洛方法实现21点最优策略寻找(MC)
21点规则简介
二十一点是一种扑克牌游戏,目标是尽量使手中牌的总点数达到 21 点,或是接近 21 点,但不能超过,然后与庄家的点数进行比较。人头牌(J、Q、K)的点数是 10。王牌可以是 11 点或 1 点,11 点时“可用”。这种游戏的整副牌是有限的(或者可以替换)。游戏开始时,每个玩家和庄家的一张牌朝上,另一张牌朝下。玩家可以请求更多的牌 (hit=1) 并决定何时停止请求牌(stick=0) 或者超过 21 点(爆牌)。玩家停止请求牌后,庄家翻开扣着的牌,并抽牌,直到所有点数之和是 17 点或大于 17 点。如果庄家爆牌,玩家获胜。
如果玩家或庄家都没爆牌,结果(输赢或持平)由谁的点数更接近 21 点来确定。赢了的奖励是 +1,平局的奖励是 0,输了的奖励是 -1。
包含以下三种状态:玩家的当前点数之和,庄家显示的一张牌(1-10,其中王牌是 1),以及玩家是否拥有可使用的王牌(0 或 1)。
一、MC状态值计算实现
可以选择实现首次经历或所有经历 MC 方法。在二十一点游戏中,首次经历和所有经历方法返回的结果一样。以首次经历的方法为例。
伪代码如下:

我们首先将研究以下策略:如果点数之和超过 18,玩家将始终停止出牌。函数 generate_episode_from_limit 会根据该策略抽取一个阶段。
该函数会接收以下输入:
bj_env:这是 OpenAI Gym 的 Blackjack 环境的实例。
它会返回以下输出:
episode:这是一个(状态、动作、奖励)元组列表,对应的是 (0,0,1,…,−1,−1,) , 其中 是最终时间步。具体而言,episode[i] 返回 (,,+1) , episode[i][0]、episode[i][1]和 episode[i][2] 分别返回 , 和 +1 。
实现代码如下:
def generate_episode_from_limit(bj_env):
episode = []
state = bj_env.reset()
while True:
action = 0 if state[0] > 18 else 1
next_state, reward, done, info = bj_env.step(action)
episode.append((state, action, reward))
state = next_state
if done:
break
return episode
print(generate_episode_from_limit(env))
out:[((7, 7, False), 1, 0.0), ((18, 7, True), 1, 0.0), ((18, 7, False), 1, -1.0)]
将有四个参数:
env:这是 OpenAI Gym 环境的实例。
num_episodes:这是通过智能体-环境互动生成的阶段次数。
generate_episode:这是返回互动阶段的函数。
gamma:这是折扣率。它必须是在 0 到 1(含)之间的值,默认值为:1。
该算法会返回以下输出结果:
V:这是一个字典,其中 V[s] 是状态 s 的估算值。
实现代码如下:
from collections import defaultdict
import numpy as np
import sys
def mc_prediction_v(env, num_episodes, generate_episode, gamma=1):
# initialize empty dictionary of lists
returns = defaultdict(list)
# loop over episodes
statess = []
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
## TODO: complete the function
episode = generate_episode(env)
states,actions,rewards = zip(*episode)
for state in states:
statess.append(state)
discouts = np.array([gamma**i for i in range(len(rewards)+1)])
for i,stage in enumerate(states):
returns[stage].append(sum(rewards[i:]*discouts[:-(i+1)]))
V = {state:np.mean(values) for state,values in returns.items()}
return V
输出结果如下:
二、MC动作值计算
先将研究以下策略:如果点数之和超过 18,玩家将几乎始终停止出牌。具体而言,如果点数之和大于 18,她选择动作 STICK 的概率是 80%;如果点数之和不大于 18,她选择动作 HIT 的概率是 80%。函数 generate_episode_from_limit_stochastic 会根据该策略抽取一个阶段。
该函数会接收以下输入:
bj_env:这是 OpenAI Gym 的 Blackjack 环境的实例。
该算法会返回以下输出结果:
episode: 这是一个(状态、动作、奖励)元组列表,对应的是 (0,0,1,…,−1,−1,) , 其中 是最终时间步。具体而言,episode[i] 返回 (,,+1) , episode[i][0]、episode[i][1]和 episode[i][2] 分别返回 , 和 +1 。
伪代码如下:

实现代码如下:
def generate_episode_from_limit_stochastic(bj_env):
episode = []
state = bj_env.reset()
while True:
probs = [0.8, 0.2] if state[0] > 18 else [0.2, 0.8]
action = np.random.choice(np.arange(2), p=probs)
next_state, reward, done, info = bj_env.step(action)
episode.append((state, action, reward))
state = next_state
if done:
break
return episode
def mc_prediction_q(env, num_episodes, generate_episode, gamma=1.0):
# initialize empty dictionaries of arrays
returns_sum = defaultdict(lambda: np.zeros(env.action_space.n))
N = defaultdict(lambda: np.zeros(env.action_space.n))
Q = defaultdict(lambda: np.zeros(env.action_space.n))
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
## TODO: complete the function
episode = generate_episode(env)
states,actions,rewards = zip(*episode)
discouts = np.array([gamma**i for i in range(len(rewards)+1)])
for i,state in enumerate(states):
returns_sum[state][actions[i]] += sum(rewards[i:]*discouts[:-(i+1)])
N[state][actions[i]] += 1
Q[state][actions[i]] = returns_sum[state][actions[i]] / N[state][actions[i]]
return Q
输出结果如下:
三、MC控制实现策略评估和策略改进
本方法先初始化动作值全为0。然后使用一个策略去进行一次游戏迭代,然后使用迭代的结果去更新动作值,最后使用生成的动作值去改进策略。
基本流程如下:

在本算法中,我们计算动作值,不再使用上面提到的动作值计算方法。而是使用增量均值算法。即不再在所有阶段结束之后再去计算平均值,而是在每次经历之后都迭代更新平均值。为此需要进行一些数学变化以更好地计算。变化过程如下:
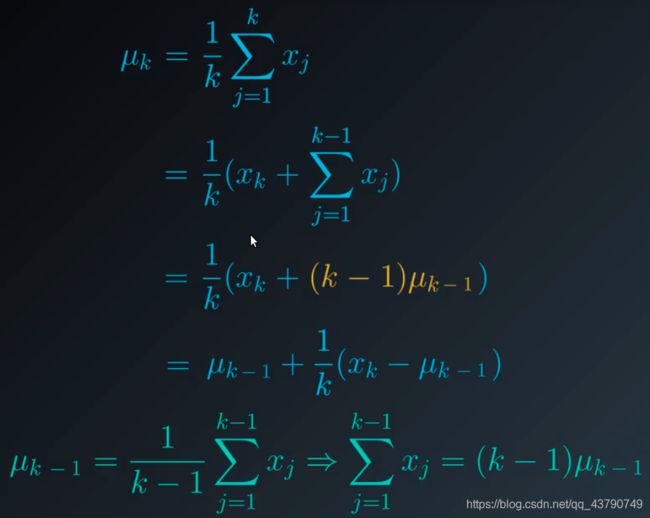
该算法可以不断估算一系列数字的均值。该算法按顺序查看每个数字,并连续地更新均值 。算法如图所示。
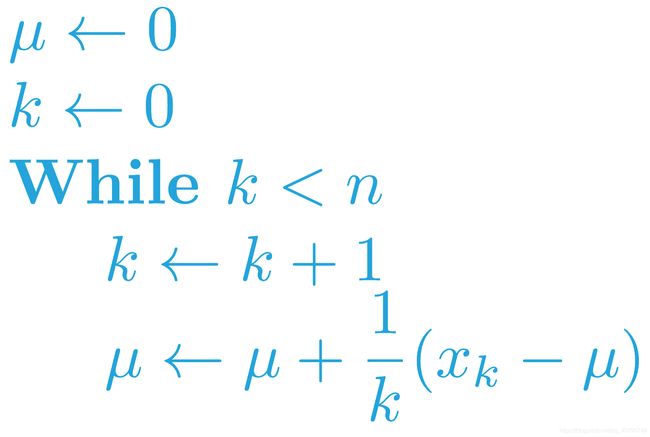
在选择策略过程中,我们一般倾向于直接选择动作值最大的方向,而不会去选择其他的方向,这样可能会导致智能体错过一些可能获得高回报的方向。因此,在本算法中,我们考虑了一种随机的方法,给最大动作值的方向较大的选择概率,给其他的方向较小的选择概率。选择方式如下:

最后得到一个GLE_MC_Control 算法,如图所示。

实现代码如下;
算法将有四个参数:
env: 这是 OpenAI Gym 环境的实例。
num_episodes:这是通过智能体-环境互动生成的阶段次数。
generate_episode:这是返回互动阶段的函数。
gamma:这是折扣率。它必须是在 0 到 1(含)之间的值,默认值为:1。
该算法会返回以下输出结果:
Q:这是一个字典(一维数组),其中 Q[s][a] 是状态 s 和动作 a 对应的估算动作值。
policy:这是一个字典,其中 policy[s] 会返回智能体在观察状态 s 之后选择的动作。
def get_prob(Q_s,nA,epsilon):
policy_s = np.ones(nA)*epsilon / nA
best_a = np.argmax(Q_s)
policy_s[best_a] = 1 - epsilon + (epsilon / nA)
return policy_s
def episode_from_epsilon(env,nA,epsilon,Q):
episode = []
state = env.reset()
sample = env.action_space.sample()
while True:
action = np.random.choice(np.arange(nA),p=get_prob(Q[state],nA,epsilon)) if state in Q else sample
next_state,reward,done,info = env.step(action)
episode.append((state,action,reward))
state = next_state
if done:
break
return episode
def update_Q_GLIE(env,nA,episilon,Q,N,gamma):
episode = episode_from_epsilon(env,nA,episilon,Q)
states,actions,rewards = zip(*episode)
discout = np.array([gamma**i for i in range(len(rewards)+1)])
for i,state in enumerate(states):
Q_old = Q[state][actions[i]]
N_old = N[state][actions[i]]
Q[state][actions[i]] = Q_old + (sum(rewards[i:]*discout[:-(i+1)])-Q_old)/(N_old+1)
N[state][actions[i]] += 1
return Q,N
def mc_control_GLIE(env,num_episodes,gamma=1.0):
nA = env.action_space.n
# initialize empty dictionaries of arrays
Q = defaultdict(lambda: np.zeros(nA))
N = defaultdict(lambda: np.zeros(nA))
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
## TODO: complete the function
episilon = 1/(i_episode/100 +1)
#episode = episode_from_epsilon(env,nA,episilon,Q)
Q,N = update_Q_GLIE(env,nA,episilon,Q,N,gamma)
policy = dict((k,np.argmax(v)) for k,v in Q.items())
return policy, Q
迭代5000000次,绘制状态值如下图。
绘制策略图如下:

四、常量alpha-MC控制算法实现策略改进
为何提出这个算法呢,是因为考虑到上面方法还有不足,上个方法会倾向于记住过去获得的经验,而实际上最近的经验更重要。
分析如下:
随着迭代次数的增加,对误差项的影响会越来越小,因此我们使用常量步长alpha代替迭代次数的倒数。
那么改进策略如下:

应该始终将 α 的值设为大于 0 并小于等于 1 之间的数字。
如果 α=0,则智能体始终不会更新动作值函数估算。
如果 α=1,则每个状态动作对的最终值估算始终等于智能体(访问该对后)最后体验的回报。
如果 α 的值更小,则促使智能体在计算动作值函数估值时考虑更长的回报历史记录。增加 α 的值确保智能体更侧重于最近抽取的回报。
实现代码如下:
def get_prob(Q_s,nA,epsilon):
policy_s = np.ones(nA)*epsilon/nA
best_action = np.argmax(Q_s)
policy_s[best_action] = 1 - epsilon + epsilon / nA
return policy_s
def episode_from_episilon_greedy(env,Q,nA,epsilon):
episodes =[]
state = env.reset()
sample = env.action_space.sample()
while True:
action = np.random.choice(np.arange(nA),p=get_prob(Q[state],nA,epsilon)) if state in Q \
else sample
next_state,reward,done,info = env.step(action)
episodes.append((state,action,reward))
state = next_state
if done:
break
return episodes
def update_Q_constant_GLIE(env,Q,nA,epsilon,alpha,gamma):
episode = episode_from_episilon_greedy(env,Q,nA,epsilon)
states,actions,rewards = zip(*episode)
discouts = np.array([gamma**i for i in range(len(rewards)+1)])
for i,state in enumerate(states):
old_Q = Q[state][actions[i]]
Q[state][actions[i]] = old_Q + alpha*(sum(rewards[i:]*discouts[:-(i+1)])-old_Q)
return Q
def mc_control_alpha(env, num_episodes, alpha, gamma=1.0):
nA = env.action_space.n
# initialize empty dictionary of arrays
Q = defaultdict(lambda: np.zeros(nA))
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
## TODO: complete the function
epsilon = 1.0/((i_episode/80000) + 1)
Q = update_Q_constant_GLIE(env,Q,nA,epsilon,alpha,gamma)
policy = {state:np.argmax(action_value) for state,action_value in Q.items()}
#policy = dict((state,np.argmax(action_value)) for state,action_value in Q.items())
return policy, Q