题目来自: https://leetcode-cn.com/problems/container-with-most-water/description/
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i,ai) 。在坐标内画 n 条垂直线,垂直线 i的两个端点分别为 (i,ai) 和 (i, 0)。找出其中的两条线,使得它们与x轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且n的值至少为 2。
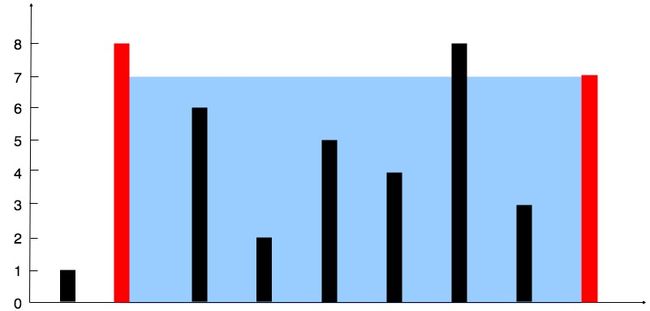
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入:[1,8,6,2,5,4,8,3,7]输出:49
一、最直接的方式是:嵌套循环遍历所有出现的容量,比较得出最大的容量,这样所需要的时间也是最长的。一般来说是有需要优化的地方的。
二、思考:
极限情况下,极限的最大容量应该是恰好两边的数值是数组中最大值和第二大值。那么我们是否一次性求出最大值?
1、是否可以从两边开始入手往里面求最大容量?这样还可以缩减范围,
2、如果是这样的话,那么就需要保证在当前的范围内以这种方式一边缩减范围一边保证我当前的范围的最大容量可以在范围内。
3、 如何保证最大容量在范围内?要知道一点的是:求最大容量时,两柱形图范围中是取较短那条长度的作为高度的,那我就可以以最长的柱形为基数,往另一边缩减范围就出最大的容量了。也就是说,我可以在宽度不断缩小的情况下,以当前范围中柱形图的最大的高度来匹配得出最大的容量。
其实我就是想 把柱形图不断的切割 求出每次的切割后的极限最大容量,然后记录下来比较。
实现代码如下:
public static void main(String[] args) {
int[] ii = { 1, 8, 6, 2, 5, 4, 8, 3, 7 };
int maxArea = maxSize(ii, 0, 0, ii.length - 1);
System.out.println("最大容量:" + maxArea);
}
public static int maxSize(int[] height, int maxArea, int left, int right) {
maxArea = Math.max(maxArea, Math.min(height[left], height[right]) * (right - left));
if (height[left] < height[right]) {
left++;
}
else {
right--;
}
if (left >= right) {
return maxArea;
}else {
return maxSize(height, maxArea, left, right);
}
}