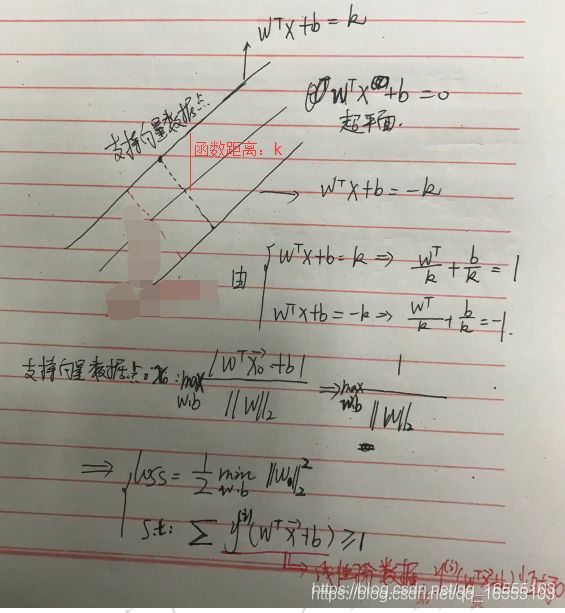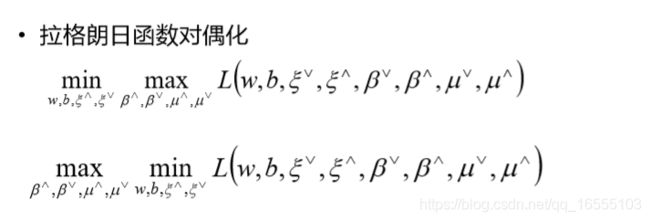SVM 支持向量机

一、SVM基础知识

  1、SVM知识回顾

     （1）梯度下降法

1、梯度下降法：
    1.1、算法目的：求凸函数极值（最值）
    1.2、适用场景：目标函数必须是凸函数（数学上称作下凹函数）
    1.3、梯度下降的公式：x1 = x1 - α * df(x1)
    1.4、BGD、SGD、MSGD的关系：
        • 当样本量为m的时候，每次迭代BGD算法中对于参数值更新一次，SGD 算法中对于参数值更新m次，MBGD算法中对于参数值
          更新m/n次，相对 来讲SGD算法的更新速度最快； 
        • SGD算法中对于每个样本都需要更新参数值，当样本值不太正常的时候， 就有可能会导致本次的参数更新会产生相反的影
          响，也就是说SGD算法的 结果并不是完全收敛的，而是在收敛结果处波动的； 
        • SGD算法是每个样本都更新一次参数值，所以SGD算法特别适合样本数 据量大的情况以及在线机器学习(Online ML)。

    1.5、梯度下降的调优：
        • 学习率的选择：学习率过大，表示每次迭代更新的时候变化比较大，有可能会跳过最优解；学 习率过小，表示每次迭代更
          新的时候变化比较小，就会导致迭代速度过慢，很长时间都不能结 束； 
        • 算法初始参数值的选择：初始值不同，最终获得的最小值也有可能不同，因为梯度下降法求解 的是局部最优解，所以一般
          情况下，选择多次不同初始值运行算法，并最终返回损失函数最小 情况下的结果值； 
        • 标准化：由于样本不同特征的取值范围不同，可能会导致在各个不同参数上迭代速度不同，为 了减少特征取值的影响，可
          以将特征进行标准化操作。

•    问题一：梯度与切线、法向向量的关系

          pass

•    问题二：BGD、SGD、MBGD

  （2）拉格朗日乘子法

1、目的：求解有约束条件函数的极值问题
2、分类：等式条件约束、不等式条件约束（KKT条件）

 

•     等式条件约束函数求极值

            pass

•    不等式条件约束函数求极值

            KKT条件，详情下文

2、对偶问题的概念

3、KKT条件

1、KKT条件的用途： KKT条件是泛拉格朗日乘子法的一种形式；主要应用在当我们的优化函数存在不等值约束的情况下的一种最优
    化求解方式；

   （1）KKT条件构造拉格朗日函数

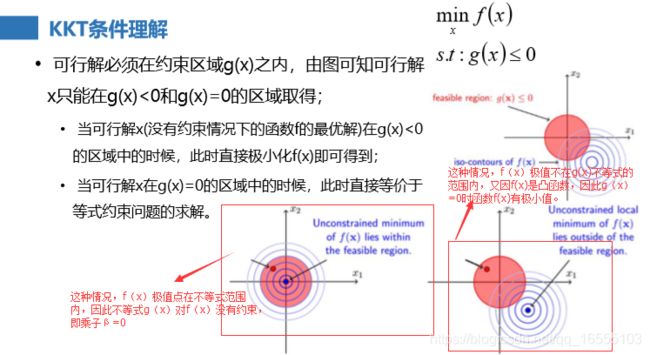
   （2）KKT条件理解

            

            理解： 

 

    （3）不等式条件拉格朗日函数计算方法

•             基本原理公式：

•             优化后：

                    最终结果：

    （4）KKT条件的总结：

 （5）KKT条件 转换等式拉格朗日函数的步骤

 

   2、高中距离知识回顾

二、感知器模型

              https://blog.csdn.net/m0_37306360/article/details/79885858      ---------- 感知机详解

1、数据线性可分：感知器模型寻找的就是一个超平面，能够把所有的二元类别分割开（允许有错误样本）。

1、感知器算法的概念：最古老的分类算法之一，原理比较简单，不过模型的分类泛化 能力比较弱，不过感知器模型是SVM、神经网络
   、深度学习等算法的基础。
2、感知器算法：只能做二分类问题，
3、感知器算法应用场景：用于线性可分数据（可以包含噪声点）
4、预测结果只有两种，决策函数 θX < 0  预测值 为 +1，θX > 0 预测值为 -1  
5、注意：感知模型求出的超平面并不是唯一的，SVM算法就是求得支持向量数据点间隔最大的超平面

•       感知器模型损失函数

                  理解： 

•      感知器模型损失函数求极值：SGD求解

 三、SVM 算法（线性可分数据）

1、SVM算法使用场景：线性分类和非线性分 类的分类应用，并且也能够直接将SVM应用于回归应用中同时通过OvR 或者OvO的方式
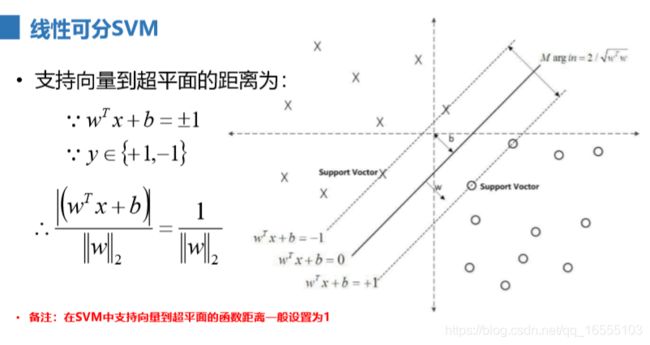
    我们也可以将SVM应用在多元分类领域中。

1、线性可分SVM

1、SVM的本质：寻找支持向量数据点间隔距离最大的超平面
2、SVM间隔距离最大的目的：提高模型的泛化能力，即提高模型的鲁棒性（防止过拟合）
3、SVM分割数据的方法：我们只要让离超平面比较近的点 尽可能的远离这个超平面(找一个最大间隔的超平面)，

 

• 线性可分(Linearly Separable)：在数据集中，如果可以找出一个超平 面，将两组数据分开，那么这个数据集叫做线性可分数据。 
• 线性不可分(Linear Inseparable)：在数据集中，没法找出一个超平面， 能够将两组数据分开，那么这个数据集就叫做线性不可
  分数据。 
• 分割超平面(Separating Hyperplane)：将数据集分割开来的直线/平 面叫做分割超平面。 
• 支持向量(Support Vector)：离分割超平面最近的那些点叫做支持向量。 
• 间隔(Margin)：支持向量数据点到分割超平面的距离称为间隔。

2、SVM损失函数的推导过程

           理解：

•        获取损失函数

3、SVM损失函数求解方法

     （1）使用KKT条件

       （2）优化计算方法 

•        第一步：求模型参数一阶导数，β看做常数

注意：w是权重系数向量，是一个列向量

                 理解：

•     第二步：将 w最小值代入 拉格朗日函数中

    （3）获得loss函数

•            由 β  >>>>> w,b值 

 

   （4）线性可分SVM算法流程

•         理解：β > 0       >>>>>>   支持向量机的样本 

    （5）例题

 

 

•           理解： 

 4、线性SVM算法的总结

• 1. 要求数据必须是线性可分的； 
• 2. 纯线性可分的SVM模型对于异常数据的预测可能会不太准； 
• 3. 对于线性可分的数据，线性SVM分类器的效果非常不错。

四、带有异常数据的线性数据的SVM算法

1、带有异常数据的线性数据：该数据是线性数据，即 本可以 可用 wx + b 的超平面将数据分隔开，但是由于数        
     据中存在异常噪声数据，导致不能用一个超平面分开。
2、注意：带有异常数据的线性数据 虽说是线性数据，但它是线性不可分的，因为他无法用硬间隔的方式分隔数据模型的准确率是 100% 。

    1、SVM的软间隔模型

1、硬间隔：上文中线性可分的数据的超平面就是一个硬间隔，它表示极其严格的划分，必须保证准确率  100% 。
2、软件隔：对于训练集的每一个样本都加入一个松弛因子，使得每个样到超平面的函数距离 >= 1，这样模型对超平面的选取就松弛了
    （即允许出现分割误差）。

 

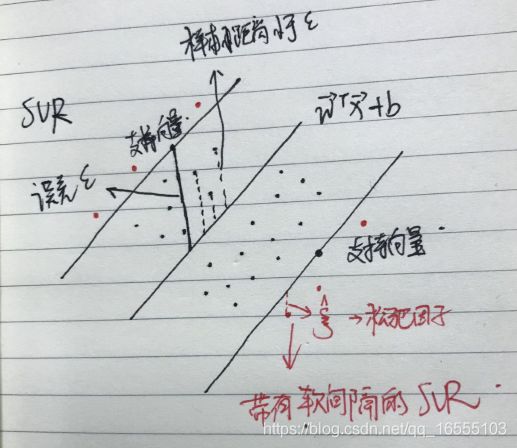
     （1）松弛因子

•         松弛因子理解：

    

 

    （2）SVM的软间隔模型 LOSS函数推导

•            不等式约束条件

1、C越小，表示模型越允许分割错误，即支持向量的样本数更多（| wx + b <= 1 |）    ------ 仅仅在skearn 库代码中；
    而数学公式中 认为 y(wx + b) = 1 是支持向量样本 

•            基于KKT条件转化等式的拉格朗日函数求极值问题

                 过程一

                 过程二

    （3）SVM的软间隔模型的 LOSS 函数

    （4）SVM的软间隔模型

•                     理解： 

    （5）SVM的软间隔模型算法流程

    （6）SVM的软间隔模型总结

• 1. 可以解决线性数据中携带异常点的分类模型构建的问题； 
• 2. 通过引入惩罚项系数(松弛因子)，可以增加模型的泛化能力，即鲁棒性； 
• 3. 如果给定的惩罚项系数C越小，表示在模型构建的时候，就允许存在越多 的分类错误的样本， 也就表示此时模型的准确率
    会比较低；如果惩罚项系数 越大，表示在模型构建的时候，就越不允许存在分类错误的样本，也就表示 此时模型的准确率
    会比较高。
------------------------------------------------------------------------------------------
• 4. 软间隔与硬间隔模型 都是线性SVM模型      ----------------- 线性模型SVM 可以获得 权重系数和截距项。

五、非线性数据的SVM算法

1、非线性数据：在当前维度数据不存在明显的线性映射关系（wx + b）
2、不管是线性可分SVM还是加入惩罚系数后的软间隔线性可分SVM其实都要 求数据本身是线性可分的，对于完全不可以线性可分
    的数据，这两种算法模 型就没法解决这个问题了

    1、多项式扩展的回顾

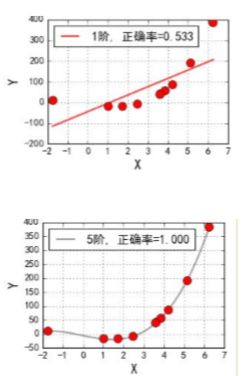
1、多项式扩展的本质：低维空间中 线性关系较弱数据，将其映射到高维空间中后，变成了 线性关系较强的数据。
2、多项式扩展的作用：一定程度解决欠拟合问题。

                       

    2、非线性可分SVM 算法的思想

1、将低维的线性关系较弱的数据通过多项式扩展转化为高维线性关系较强的数据，从而就可以使用线性可分SVM模型或者软间隔线性
    可分SVM模型。

    3、非线性可分SVM 算法LOSS函数

     4、非线性可分SVM 算法多项式扩展的局限性

1、拿到非线性数据，就找一个映射， 然后一股脑把原来的数据映射到新空间中，再做线性 SVM 即可。不过事 实上没有这么简单！
    其实刚才的方法稍想一下就会发现有问题：在最初 的例子里做了一个二阶多项式的转换，对一个二维空间做映射，选择的 新空
    间是原始空间的所有一阶和二阶的组合，得到了5个维度；如果原始 空间是三维，那么我们会得到9维的新空间；如果原始空间是
    n维，那么 我们会得到一个n(n+3)/2维的新空间；这个数目是呈爆炸性增长的，这 给计算带来了非常大的困难，而且如果遇到无
    穷维的情况，就根本无从 计算。

     5、非线性可分SVM的核函数

1、核函数的基本思想：由于多项式扩展数据特征属性的维度后，LOSS损失函数的计算方法不变，只是需要计算特征属性扩展后的
    特征向量的点积，因此可以定义一个函数（自变量是原数据的特征属性向量 x.T 与 x），用其函数值来代替高维的特征属性
    向量点积。
2、核函数的本质：用低维的特征向量函数值来代替高维特征向量的内积值，已达到用低维度的计算量来近似得到高维度扩展的效果。 
    通过核函数，可以将非线性可分的数据转换为线性可分数据来进行SVM划分
3、注意：带有核函数的非线性SVM算法本质上没有扩展维度，因此并不能获取 模型的权重系数和截距项。

        （1）核函数的定义

        （2）核函数的理解

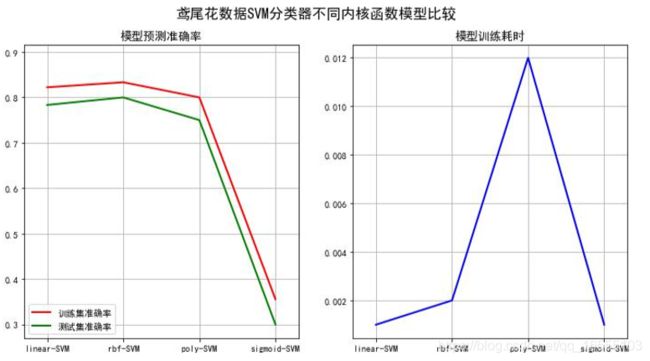
         （3）常见的核函数

 

           （4）核函数总结

           （5）不同核函数的效果

六、SMO算法

1、SMO算法：序列最小优化算法(Sequential minimal optimization, SMO)是一种用于解决 SVM训练过程中所产生的优化问题
    的算法           ------------ 目的：求使得目标函数最小时的β
2、SMO算法的思想：
    • 从而可以得到解决问题的思路如下： 
        • 首先，初始化后一个β值，让它满足对偶问题的两个初始限制条件； 
        • 然后不断优化这个β值，使得由它确定的分割超平面满足g(x)目标条件； 而且在优化过程中，始终保证β值满足初始限
          制条件。 
    • 备注：这个求解过程中，和传统的思路不太一样，不是对目标函数求最小值，而是让g(x)目标条件尽可能的满足，且每一
          次迭代都使得目标函数不断减小

    • 因为目标函数中存在m个变量，直接优化比较难，利用启发式的 方法/EM算法的思想，每次优化的时候，只优化两个变量，将
      其它的变量看成常数项，这 样SMO算法就将一个复杂的优化算法转换为一个比较简单的两变量优化问题了。

SMO算法两个基本原则：
    • 每次优化的时候，必须同时优化β的两个分量（优化两个分量是为了满足初始化条件，因为如果只优化一个分量的话，新的β值
      就没法满足初始限制条件中的等式约束条件了。而优化多个分量计算量较大）。
    • 每次优化的两个分量应该是违反g(x)目标条件比较多的（即 | E1 - E2 | 最大的）。也就是说，本来应当是大于等于1的，
      越是小于1违反g(x)目标条件就越多。 

•    β初始值的定义 

1、β的初始值通常将所有的正例样本计数m，所有负例样本计数n，则正例样本β的初始值为x/m （x是0<= β <= C间的一个值），负例样
    本β的初始值为x/n

  1、SMO算法的推导过程

    （1）基本知识

    （2）SMO算法的目标条件

     （3）SMO算法结果公式

       （4）例题

 

 七、SVM回归算法的理解

   1、SVM回归算法SVR

1、SVR原理理解：
    1.1、给定误差ε，寻找支持向量（使得支持向量到超平面的间隔最大(相比于分类SVC，SVR寻找的是较远的点作为支持向量)），并
        且使得大部分的样本尽量离超平面较近，即处于支持向量与超平面之间。
    1.2、当数据不能达到上诉条件时，我们也可以用SVC中软间隔的思想。

                            

    2、SVR的不等式约束

       （1）未加松弛因子

      （2）加松弛因子

   3、KKT条件的朗日函数 

 

 

 4、SVR的LOSS函数

八、SVM API 使用

1、线性的SVM（LinearSVC、LinearSVR）

利用liblinear实现回归的可扩展线性支持向量机

class sklearn.svm.LinearSVC(penalty='l2', loss='squared_hinge', dual=True, tol=0.0001, 
    C=1.0, multi_class='ovr', fit_intercept=True, intercept_scaling=1, class_weight=None, 
    verbose=0, random_state=None, max_iter=1000)
'''
        C=1.0                           松弛因子系数
        penalty='l2'                    线性回归的正则项
        loss='squared_hinge'            损失函数
        tol=0.0001                      容忍停止标准
        multi_class='ovr'               多分类
        max_iter=1000                   要运行的最大迭代次数。
'''

class sklearn.svm.LinearSVR(epsilon=0.0, tol=0.0001, C=1.0, loss='epsilon_insensitive', 
    fit_intercept=True, intercept_scaling=1.0, dual=True, verbose=0, random_state=None, 
    max_iter=1000)

'''
        epsilon=0.0                         ---------- 回归允许误差
        tol = 0.0001
        C = 1.0
        loss ='epsilon_insensitive'  'epsilon_insensitive'或'squared_epsilon_insensitive'
                                     损失函数（默认是）epsilon_insensitive，'l1'是epsilon不        
                                     敏感的损失（标准SVR），而'l2'是平方的epsilon不敏感的损失。
               
        fit_intercept = True
'''

2、带有核函数的SVM（SVC，SVR）

     （1）SVC、SVR

from sklearn import tree
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import classification_report
from sklearn.externals import joblib
from sklearn.svm import SVC

--------------------------------------------------------------------------------------------
class sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, 
    shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, 
    verbose=False, max_iter=-1, decision_function_shape=None, random_state=None)
 """
        C: 惩罚性系数，C值越大，表示越不允许模型在训练数据上出错，也就是模型容易导致过拟合
        kernel：核函数，可选值：poly、rbf、linear，一般选择默认rbf即可。
        gamma：gamma反映了做rbf核函数的时候，映射到高维空间中的特征分布情况。gamma值越小，模型的泛化能力越强(测试)，
            但是过小的话，就会退化成为线性的SVM模型，gamma值越大，就表示越关注样本附件的样本数据点，模型会更多的关注细节
            信息，也就是理论上来讲，当gamma足够大的时候，可以让模型拟合任意非线性数据(训练)。
        probability: 是否计算概率值，默认是不计算概率值。
        degree    多项式核函数的次数（'poly'）。被所有其他内核忽略。
        coef0     核函数中的独立项。它只在'poly'和'sigmoid'中很重要
        tol       容忍停止标准
        max_iter=-1          求解器内迭代的硬限制，或无限制的-1。  

    NOTE: 有的时候为了比较好的均衡过拟合以及欠拟合的情况，一般选择C值比较大，gamma比较小的值。如果模型过拟合，减小C
            值或者减小gamma值; 如果模型欠拟合，增大C或者gamma值。一般情况下，取值范围:[1e-6,1e-5,1e-4,1e-3,1e-2,
            1e-1,1.0,10.0100.0]
    NOTE: gamma值越大，支持向量越少，gamma值越小的，支持向量越多。

 """

class sklearn.svm.SVR(kernel='rbf', degree=3, gamma='auto', coef0=0.0, tol=0.001, C=1.0, 
    epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)
'''
        epsilon=0.1                         ---------- 回归允许误差
'''

 

   （2）支持向量机用于使用libsvm

支持向量机用于使用libsvm实现的回归，使用参数来控制支持向量的数量。

--------------------------------------------------------------------------------------------
class sklearn.svm.NuSVC(nu=0.5, kernel='rbf', degree=3, gamma='auto', coef0=0.0, 
    shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, 
    verbose=False, max_iter=-1, decision_function_shape=None, random_state=None)
'''
        nu=0.5             作用相当于SVC、SVR中的 参数C
'''

class sklearn.svm.NuSVR(nu=0.5, C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0,     
    shrinking=True, tol=0.001, cache_size=200, verbose=False, max_iter=-1)

   （3）选取异常样本SVM

1、作用相当于集成学习中的 IF 算法        ------------- 用于检测异常样本

class sklearn.svm.OneClassSVM(kernel='rbf', degree=3, gamma='auto', coef0=0.0, tol=0.001, 
    nu=0.5, shrinking=True, cache_size=200, verbose=False, max_iter=-1, random_state=None)