机器学习之PCA:主成分分析（二、算法案例）

目录

一、降维实例

二、鸢尾花数据集降维 

---

一、降维实例

data数据下载，提取码：fobw

导入库、载入数据并可视化：

import numpy as np
import matplotlib.pyplot as plt

data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
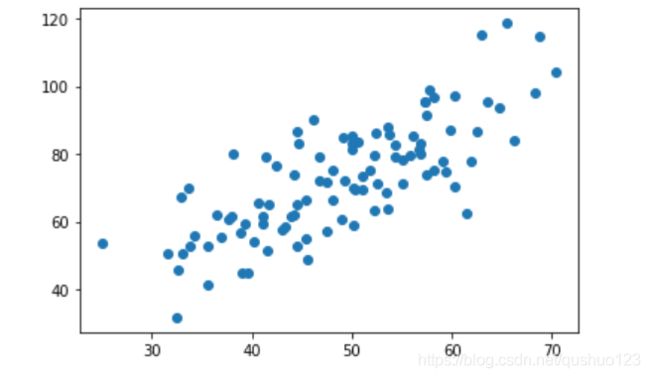
plt.scatter(x_data,y_data)
plt.show()

画出的图如下：

 

数据中心化，减去均值以用来求协方差矩阵：

# 数据中心化
def zeroMean(dataMat):
    # 按列求平均，即各个特征的平均
    meanVal = np.mean(dataMat, axis=0) 
    newData = dataMat - meanVal
    return newData, meanVal

newData,meanVal=zeroMean(data) 
# np.cov用于求协方差矩阵，参数rowvar=0说明数据一行代表一个样本
covMat = np.cov(newData, rowvar=0)

求特征值并对其排序，选择最大的k个：

# np.linalg.eig求矩阵的特征值和特征向量
eigVals, eigVects = np.linalg.eig(np.mat(covMat))

# 对特征值从小到大排序
eigValIndice = np.argsort(eigVals)

k = 1
# 最大的k个特征值的下标
n_eigValIndice = eigValIndice[-1:-(k+1):-1]

求特征向量并计算投影：

# 最大的n个特征值对应的特征向量
n_eigVect = eigVects[:,n_eigValIndice]

# 低维特征空间的数据
lowDDataMat = newData*n_eigVect

print(lowDDataMat)

 最后将输出一维数据。

最后可以看一下恢复后的数据与原数据的对比：

# 利用低纬度数据来重构数据
reconMat = (lowDDataMat*n_eigVect.T) + meanVal

# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)

# 重构的数据
x_data = np.array(reconMat)[:,0]
y_data = np.array(reconMat)[:,1]
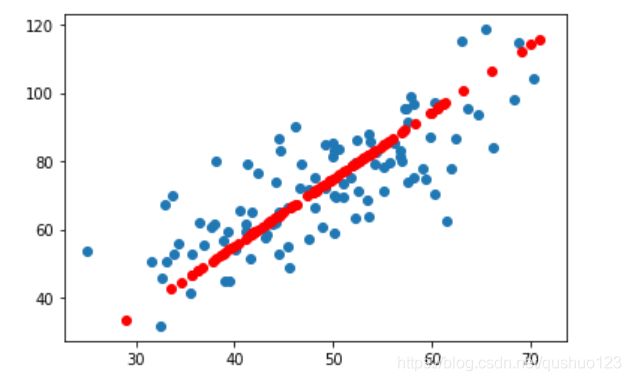
plt.scatter(x_data,y_data,c='r')
plt.show()

最终得到的图如下，蓝色点为原数据，红色点为恢复后的数据： 

 

二、鸢尾花数据集降维 

 导入库并下载数据集：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler

iris = load_iris()
#均值归一化
data = StandardScaler().fit_transform(iris.data)

mean = np.mean(data,axis=0)
cov = (data - mean).T.dot(data - mean)/(data.shape[0]-1)
#cov = np.cov(data.T)
eigVals, eigVects = np.linalg.eig(np.mat(cov))
#特征值从小到大排序
eigValIndice = np.argsort(eigVals)
k = 2
# 最大的k个特征值的下标，从右向左找
n_eigValIndice = eigValIndice[-1:-(k+1):-1]

matx = np.hstack((eigVects[:,n_eigValIndice[0]].reshape(4,1),eigVects[:,n_eigValIndice[1]].reshape(4,1)))
# 低维特征空间的数据
lowdata = data*matx

#画图

x = np.array(lowdata[0:50,0])
y = np.array(lowdata[0:50,1])
plt.scatter(x,y,label='setosa')
x = np.array(lowdata[50:100,0])
y = np.array(lowdata[50:100,1])
plt.scatter(x,y,c='r',label='versicolor')
x = np.array(lowdata[100:150,0])
y = np.array(lowdata[100:150,1])
plt.scatter(x,y,c='black',label='virginica')
plt.rcParams['font.sans-serif']=['simhei']#在画图中显示中文
plt.xlabel('主成分1')
plt.ylabel('主成分2')
plt.legend()
plt.show()

降维后画出的图如下：