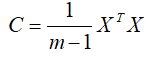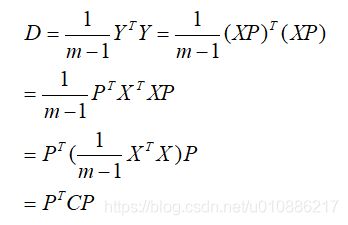机器学习（4）：PCA主成分分析法实例

一、简介

1.Principal Component Analysis

2.用途：降维中最常用的一种手段，可用于数据压缩、提取重要信息等领域。

3.目标：基于方差提取最有价值的信息

二、PCA求解原理

1.优化目标

（1）第一个目标：将一组N维向量降为K维（K大于0，小于N），目标是选择K个单位（模为1）正交基，使原始数据变换到这组基上后，各字段两两间协方差为0

（2）第二个目标：每个字段的方差，则尽可能大（在正交的约束下，取最大的K个方差）

2.优化目标和协方差矩阵关系

（1）推倒原始矩阵与基变换矩阵后矩阵的关系。

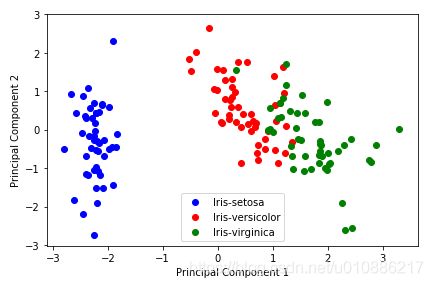
假设原始X=(X1,X2,...,Xn）有N个特征，每个特征有m条数据，即m*n的矩阵。目标将为K（k

即：Y=XP

（2）推倒原始矩阵的协方差矩阵C与基变换矩阵后矩阵的协方差矩阵D的关系。

设原始矩阵的协方差矩阵维C，变换基维P，则Y=PX。其中C为

通过基变换降维后的协方差D为

（3）由协方差矩阵推出的优化目标：

寻找一个矩阵P，满足PTCP是一个对角矩阵，并且对角元素按从大到小依次排列，那么P的前K列就是要寻找的基，用X乘以P的前K列组成的矩阵就使得X从N维降到了K维并满足上述优化条件。

3.变换矩阵P的求解原理

（1）协方差矩阵C是一个实对称矩阵，实对称矩阵有性质：

（a）实对称矩阵不同特征值对应的特征向量必然正交。

（b）设特征向量λλ重数为r，则必然存在r个线性无关的特征向量对应于λλ，因此可以将这r个特征向量单位正交化

（2）所以针对实对称矩阵C，一定可以找到n个单位正交特征向量，设这n个特征向量为e1,e2,e3,..,en，组成矩阵：

P=（e1 e2 e3 ... en），这个P可以使C对角化：

 

三、PCA实现步骤

假设有m条n维数据

1.将原始数据按列组成m行n列矩阵X

2.将X的每一列（代表一个属性字段）进行零均值化，即减去这一行的均值

3.求出协方差矩阵

4.求出协方差矩阵的特征值及对应的特征向量

5.将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k列组成矩阵P

6.Y=XP即为降维到k维后的数据(m×k)

四、python代码实例（python3.7）

实例采用常用的iris.data数据集

1.读取数据，并且设定第一行名称

import numpy as np
import pandas as pd
df = pd.read_csv('iris.data')
df.head()

df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
df.head()

结果：

	sepal_len	sepal_wid	petal_len	petal_wid	class
0	4.9	3.0	1.4	0.2	Iris-setosa
1	4.7	3.2	1.3	0.2	Iris-setosa
2	4.6	3.1	1.5	0.2	Iris-setosa
3	5.0	3.6	1.4	0.2	Iris-setosa
4	5.4	3.9	1.7	0.4	Iris-setosa

2.将数据集分为数据类X和类别类Y

# split data table into data X and class labels y

X = df.iloc[:,0:4].values

y = df.iloc[:,4].values

3.将X的每一列（代表一个属性字段）进行零均值化

from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)
print (X_std)

4.求取X的协方差矩阵

（1）方法一：按照定义

mean_vec = np.mean(X_std, axis=0)
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
print('Covariance matrix \n%s' %cov_mat)
结果：
Covariance matrix 
[[ 1.00675676 -0.10448539  0.87716999  0.82249094]
 [-0.10448539  1.00675676 -0.41802325 -0.35310295]
 [ 0.87716999 -0.41802325  1.00675676  0.96881642]
 [ 0.82249094 -0.35310295  0.96881642  1.00675676]]

（2）方法二：numpy求取协方差的函数cov

print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))
结果：
NumPy covariance matrix: 
[[ 1.00675676 -0.10448539  0.87716999  0.82249094]
 [-0.10448539  1.00675676 -0.41802325 -0.35310295]
 [ 0.87716999 -0.41802325  1.00675676  0.96881642]
 [ 0.82249094 -0.35310295  0.96881642  1.00675676]]

注意：输入一定要是n*m，n为特征个数，m为样本数目。即cov输入需要为：

5.求取协方差矩阵的特征值和特征向量

cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)

print('Eigenvectors \n%s' %eig_vecs)
print('\nEigenvalues \n%s' %eig_vals)

结果：
Eigenvectors 
[[ 0.52308496 -0.36956962 -0.72154279  0.26301409]
 [-0.25956935 -0.92681168  0.2411952  -0.12437342]
 [ 0.58184289 -0.01912775  0.13962963 -0.80099722]
 [ 0.56609604 -0.06381646  0.63380158  0.52321917]]

Eigenvalues 
[2.92442837 0.93215233 0.14946373 0.02098259]

6.特征值和特征向量由高到低排序

# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
print (eig_pairs)
print ('----------')
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)

#打印
# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in descending order:')
for i in eig_pairs:
    print(i[0])

结果：
[(2.9244283691111144, array([ 0.52308496, -0.25956935,  0.58184289,  0.56609604])), (0.932152330253508, array([-0.36956962, -0.92681168, -0.01912775, -0.06381646])), (0.14946373489813417, array([-0.72154279,  0.2411952 ,  0.13962963,  0.63380158])), (0.02098259276427019, array([ 0.26301409, -0.12437342, -0.80099722,  0.52321917]))]
----------
Eigenvalues in descending order:
2.9244283691111144
0.932152330253508
0.14946373489813417
0.02098259276427019

7.取特征值最大的前2个特征向量，组成转换基P=4×2维

P=np.hstack((eig_pairs[0][1].reshape(4,1),
                      eig_pairs[1][1].reshape(4,1)))
print('Matrix P:\n', P)

结果：
Matrix P:
 [[ 0.52308496 -0.36956962]
 [-0.25956935 -0.92681168]
 [ 0.58184289 -0.01912775]
 [ 0.56609604 -0.06381646]]

8.验证结果

（1）降维后矩阵Y=XP

Y = X_std.dot(matrix_w)
结果：
array([[-2.10795032,  0.64427554],
       [-2.38797131,  0.30583307],
       [-2.32487909,  0.56292316],
       [-2.40508635, -0.687591  ],
       [-2.08320351, -1.53025171],
       [-2.4636848 , -0.08795413],
        ......
       [ 1.54200377,  0.90808604],
       [ 1.50925493, -0.26460621],
       [ 1.3690965 , -1.01583909],
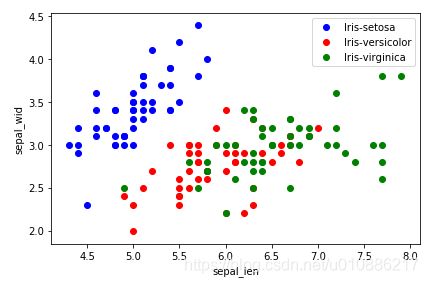
       [ 0.94680339,  0.02182097]])

（2）降维前原始数据的绘图

plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
                        ('blue', 'red', 'green')):
     plt.scatter(X[y==lab, 0],
                X[y==lab, 1],
                label=lab,
                c=col)
plt.xlabel('sepal_len')
plt.ylabel('sepal_wid')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

结果：

（3）降维后的矩阵Y针对不同分类采用不同颜色绘图

plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
                        ('blue', 'red', 'green')):
     plt.scatter(Y[y==lab,0],
                Y[y==lab,1],
                label=lab,
                c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()

结果：

（4）结论：由（2）和（3）中图可以看出，经过PCA后，基本核心特征被保留，分类的结果更加明显。

五、参考

1.PCA的数学原理，作者：张洋，链接：http://blog.codinglabs.org/articles/pca-tutorial.html