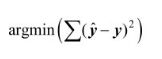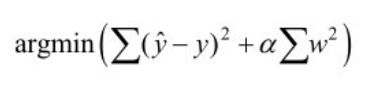1.最小二乘法(Least Square Method)：
基于均方误差最小化来进行模型求解的方法
LSM
可直接使用sklearn.linear_model中的LinearRegression对象进行训练与预测
不足：
最小二乘法会随着特征维度的增加出现模型的过度拟合
例子
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
def make_data(nDim):
x0=np.linspace(1,np.pi,50)
x=np.vstack([[x0,],[i**x0 for i in range(2,nDim+1)]])
y=np.sin(x0)+np.random.normal(0,0.15,len(x0))
return x.transpose(),y
x,y=make_data(12)
def linear_regression():
dims=[1,3,6,12]
for idx, i in enumerate(dims):
plt.subplot(2,len(dims)/2,idx+1)
reg=linear_model.LinearRegression()
sub_x=x[:,0:i]
reg.fit(sub_x,y)
plt.plot(x[:,0],reg.predict(sub_x))
plt.plot(x[:,0],y,".")
plt.title("dim=%s"%i)
print("dim %d :"%i)
print("intercept %s"% (reg.intercept_,))
print("coef :%s"%(reg.coef_,))
plt.show()
linear_regression()
LSM
并且发现随着特征维度的增加，模型求得的w的值也增加。
根据最小二乘法的原理，为了更好地拟合训练数据中很小的x值差异产生的较大的y值差异，必须使用较大的w值，而越大的w值会导致预测目标值变大，所以产生过拟合。
2.岭回归(Ridge Regression)
对最小二乘法的改进，添加了一个惩罚项(L2 Penalty)
可解决多特征情况下回归模型参数太大，导致过拟合的问题。
Ridge
α是一个可以调节的超参数
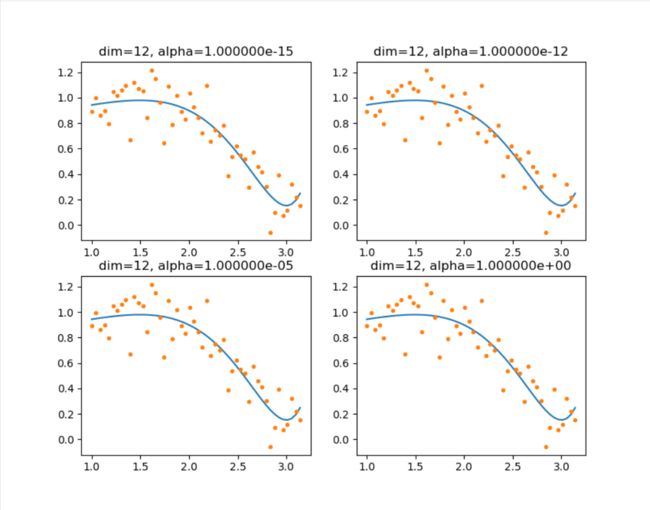
def ridge_regression():
alphas=[1e-15,1e-12,1e-5,1,]
for idx, i in enumerate(alphas):
plt.subplot(2,len(alphas)/2,idx+1)
reg=linear_model.Ridge(alpha=1)
sub_x=x[:,0:12]
reg.fit(sub_x,y)
plt.plot(x[:,0],reg.predict(sub_x))
plt.plot(x[:,0],y,".")
plt.title("dim=12, alpha=%e"%i)
print("dim %d :"%i)
print("intercept %s"% (reg.intercept_,))
print("coef :%s"%(reg.coef_,))
plt.show()
ridge_regression()
Ridge
对比最小二乘法的结果，岭回归中模型参数w显著降低，且α越大，回归参数越小，模型越平缓。
3.Lasso回归
注意到在岭回归中，无论将α设多大，回归模型的参数都有很小小的绝对值，很难达到零值。而Lasso回归可以将不重要的特征参数计算为0的模型。
Lasso
|w|为L1 Penalty
def lasso_regression():
alphas=[1e-10,1e-3,1,10,]
for idx, i in enumerate(alphas):
plt.subplot(2,len(alphas)/2,idx+1)
reg=linear_model.Lasso(alpha=i)
sub_x=x[:,0:12]
reg.fit(sub_x,y)
plt.plot(x[:,0],reg.predict(sub_x))
plt.plot(x[:,0],y,".")
plt.title("dim=12, alpha=%e"%i)
print("dim %d :"%i)
print("intercept %s"% (reg.intercept_,))
print("coef :%s"%(reg.coef_,))
plt.show()
lasso_regression()
Lasso
总结
Conclusion
Conclusion