深度优先搜索 - DFS（暴搜）

DFS思路应用-穷举求解问题

在无路可走时，我们往往会选择搜索算法，因为我们期望利用计算机的高性能来有目的的穷举一个问题的部分甚至所有可能情况，从而在这些情况中寻找符合题目要求的答案。这也是“爆搜”之名的  由来

我们约定，对于问题的介入状态，叫初始状态，要求的状态叫目标状态。
这里的搜索就是对实时产生的状态进行分析检测，直到得到一个目标状态或符合要求的最佳状态为止。对于实时产生新的状态的过程叫扩展（由一个状态，应用规则，产生新状态的过程）

搜索的要点：

1. 选定初始状态，在某些问题中可能是从多个合法状态分别入手搜索；

2. 遍历自初始状态或当前状态所产生的合法状态，产生新的状态并进入递归；

3. 检查新状态是否为目标状态，是则返回，否则继续遍历，重复2-3步骤

对状态的处理：DFS时，用一个数组存放产生的所有状态

1. 把初始状态放入数组中，设为当前状态；
2. 扩展当前的状态，从合法状态中旬寻找一个新的状态放入数组中，同时把新产生的状态设为当前状态；
3. 判断当前状态是否和前面的状态重复，如果重复则回到上一个状态，产生它的另一状态；
4. 判断当前状态是否为目标状态，如果是目标目标状态，则找到一个解答，根据实际问题需求，选择继续寻找答案或是直接返回。
5. 如果数组为空，说明对于该问题无解。

 

目录

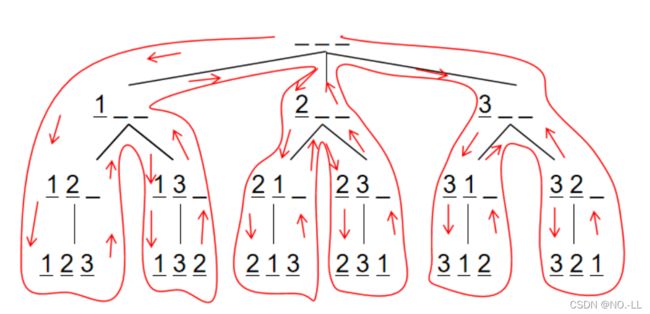
842. 排列数字

843. n-皇后问题

P1036 [NOIP2002 普及组] 选数

题1与题3的结合练习：

        P1157 组合的输出

---

842. 排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤7

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

 先画出递归搜索树

思路： 

• 用 path 数组保存排列，当排列的长度为 n 时，是一种方案，输出。
• 用 st 数组表示数字是否用过。当 st[i] 为 1 时：i 已经被用过，st[i] 为 0 时，i 没有被用过。
• dfs(i) 表示的含义是：在 path[i] 处填写数字，然后递归的在下一个位置填写数字。
• 回溯：第 i 个位置填写某个数字的所有情况都遍历后， 第 i 个位置填写下一个数字。

#include
using namespace std;
const int N=10;
int n;
int path[N];
bool st[N];

void dfs(int u)
{
    if(u==n)
    {
        for(int i=0;i>n;
    dfs(0);
    return 0;
}

843. n-皇后问题

n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

方法1、（DFS按行枚举） 时间复杂度O(n*n!)

代码分析

对角线 dg[u+i]，反对角线udg[n−u+i]中的下标 u+i 和 n−u+i 表示的是截距

下面分析中的(x,y)相当于上面的(u,i)
反对角线 y=x+b 截距 b=y−x，因为我们要把 b 当做数组下标来用，显然 b 不能是负的，所以我们加上 +n （实际上+n+4,+2n都行），来保证是结果是正的，即 y - x + n
而对角线 y=−x+b, 截距是 b=y+x，这里截距一定是正的，所以不需要加偏移量

核心目的：找一些合法的下标来表示dg或udg是否被标记过，所以如果你愿意，你取 udg[n+n−u+i] 也可以，只要所有(u,i)对可以映射过去就行

总结：因为斜线斜率相同，所以唯一区分就是截距，截距相同则是同一条斜线
 

#include 
using namespace std;
const int N = 20; 

// bool数组用来判断搜索的下一个位置是否可行
// col列，dg对角线，udg反对角线
// g[N][N]用来存路径

int n;
char g[N][N];
bool col[N], dg[N], udg[N];

void dfs(int u) {
    // u == n 表示已经搜了n行，故输出这条路径
    if (u == n) {
        for (int i = 0; i < n; i ++ ) puts(g[i]);   // 等价于cout << g[i] << endl;
        puts("");  // 换行
        return;
    }

    //对n个位置按行搜索
    for (int i = 0; i < n; i ++ )
        // 剪枝(对于不满足要求的点，不再继续往下搜索)  
        // udg[n - u + i]，+n是为了保证下标非负
        if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 这步很关键
            g[u][i] = '.';

        }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0);

    return 0;
}   

方法2、（DFS按每个元素枚举）时间复杂度O(2^(n^2))

#include 
using namespace std;
const int N = 20;

int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // 因为是一个个搜索，所以加了row

// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
    // 因为从0开始，y==n时超出边界，处理超出边界的情况
    if (y == n) y = 0, x ++ ;

    if (x == n) { // x==n说明已经枚举完n^2个位置了
        if (s == n) { // s==n说明成功放上去了n个皇后
            for (int i = 0; i < n; i ++ ) puts(g[i]);
            puts("");
        }
        return;
    }

    // 分支1：放皇后
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1);
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
        g[x][y] = '.';
    }

    // 分支2：不放皇后
    dfs(x, y + 1, s);
}


int main() {
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0, 0, 0);

    return 0;
}

P1036 [NOIP2002 普及组] 选数

知 n 个整数 x1,x2,…,xn，以及11个整数 k (k < n)。从 n 个整数中任选 k 个整数相加，可分别得到一系列的和。例如当 n = 4,k = 3 , 4个整数分别为3,7,12,1时，可得全部的组合与它们的和为：

3+7+12=2

3+7+19=2

7+12+19=3

3+12+19=3

现在，要求你计算出和为素数共有多少种。

例如上例，只有一种的和为素数：3+7+19=2。

输入格式

键盘输入，格式为：

n , k (1 <= n <= 20 , k < n)
x1,x2,…,xn(1 <= xi <= 5000000)

输出格式

屏幕输出，格式为： 1个整数（满足条件的种数）。

输入输出样例

输入

4 3
3 7 12 19

输出

1

思路 

不降原则
因为是求种类数 ，所以需要去重，有点麻烦，所以就按照从小到大的顺序全排列

例如，在1 2 3 4，四个数字中选三个数字
1 2 3
1 2 4
1 3 4
因为123跟213，231，312…虽然顺序不同，但是本体是求和，他们的和都相等，是重复的结果

所以，从大到小输出，避免重复

具体实现，看下列代码，dfs函数的参数ks，就代表当前选择的数字在全部数字中的位置是第ks个，
for循环也是从第ks个开始，省去了循环的时间，而且也在避免重复
之后dfs递归i+1，自动选择比它大的数字进行排序
 

#include
#include
using namespace std;
const int N=21;

int n,sum,k,tot;
int a[N];

int zs(int n)
{
	if(n<2) return 0;
	for(int i=2;i<=sqrt(n);i++)
		if(n%i==0) return 0;
	return 1;
}

void dfs(int m,int sum,int ks)//开始坐标防止重复
							  //如出现1+2+3和1+3+2 
{
	if(m==k)
	{
		if(zs(sum))
		{
			tot++;
		}
		return ;
	}
	
	for(int i=ks;i>n>>k;
	for(int i=0;i>a[i];
	dfs(0,0,0);	//层数，加和，开始坐标 
	cout<

题1与题3的结合练习：

P1157 组合的输出

输入 #1

5 3 

输出 #1

  1  2  3
  1  2  4
  1  2  5
  1  3  4
  1  3  5
  1  4  5
  2  3  4
  2  3  5
  2  4  5
  3  4  5

思路：画树+不降原则

#include
using namespace std;

int n,k;
int a[22];
bool st[22];
void dfs(int m,int ks)
{
	if(m==k)
	{
		for(int i=0;i>n>>k;
	dfs(0,1);
	return 0;
} 

感觉搜索终于入门了......