后缀数组
数组的定义
一下排名均是在字典序下的排名
\(sa[i]\):排名为\(i\)的后缀的编号
\(rank[i]\):第\(i\)个后缀串的排名
有\(rank[sa[i]]=i\)和\(sa[rank[i]]=i\)
\(height[i]\):排名为\(i\)的后缀和排名为\(i-1\)的后缀的最长公共前缀
模板:
#include
#include
#include
using namespace std;
const int N = 1e6 + 5;
int n, m;
char s[N];
int sa[N], x[N], y[N], rk[N], height[N], c[N];
void get_sa()
{
//基数排序o(n)
//先对第一关键字(模式串出现的字母)排序
for (int i = 1; i <= n; i++) c[x[i] = s[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i > 0; i--) sa[c[x[i]]--] = i;
for (int k = 1; k <= n; k <<= 1)
{
int num = 0;
//以长度为k,i为第一关键字,i+k为第二关键字
for (int i = n - k + 1; i <= n; i++) y[++num] = i; //从n-k+1开始第二关键字为空字符,最小,所以排最前面
for (int i = 1; i <= n; i++) //实际上只有n-k个数
if (sa[i] > k) y[++num] = sa[i] - k;
//对第二关键字排序
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
if (num == n)break;
m = num;
}
}
void get_height()
{
for (int i = 1; i <= n; i++) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i++)
{
if (rk[i] == 1) continue;
if (k) k--;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
int main()
{
scanf("%s", s + 1);
n = strlen(s + 1), m = 122;//字母z的ASCLL值为122;
get_sa();
get_height();
return 0;
}
应用
\(1.\)求本质不同的子串的个数:
普通做法是枚举左右端点然后哈希判重。考虑我们当前枚举到的左端点是\(l\),那么我们右端点就要依次枚举\(l+1,l+1,...,n\),发现,其实就是枚举第\(l\)个后缀的所有前缀。然后考虑如何判重,将第\(l\)个后缀的所有前缀按字典序排序记为,通过\(height\)数组我们知道排名相邻的两个串的最长公共前缀,先记他们的长度依次是\(len_1,len_2,...,len_{n-l+1}\),那么第一个穿可以产生\(len_1\)个前面没有出现过的串(因为是第一个,所以不需要判重),再考虑第二个串,很容易知道第二个串贡献的不同的串个数为\(len_2-height[2]\),\(height[2]\)记录的是第二个串和第一个串的最长共前缀,这部分在第一个串中被统计过了,所以不需要再统计。综上,所有的答案就是\(\sum_{i=1}^nlen_i-height[i]\)就是答案。
例题:\(生成魔咒\)
题意:每次加入一个字符,问此时本质不同的子串的数量
Sol:正向加不好做,考虑先把所有字符加入后,翻转(翻转和正向的答案其实是一样的)后从前往后依次删掉字符然后求答案。假设翻转后的串为\(S\),将\(S\)的所有后缀排序后,每次从前删掉一个字符是,相当于删去一个后缀,\(sa\)数组利用链表维护,假设删掉的后缀排名为\(i\),那么第\(i-1\)和第\(i+1\)的串的最长公共前缀即\(height[i+1]=min(height[i],height[i+1])\)的。然后按照上面的方法求解即可。
#include
#define ll long long
using namespace std;
const int N = 1e6 + 5;
int n, m;
int s[N],l[N],r[N];
int sa[N], x[N], y[N], rk[N], height[N], c[N];
void get_sa()
{
//基数排序o(n)
//先对第一关键字(模式串出现的字母)排序
for (int i = 1; i <= n; i++) c[x[i] = s[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i > 0; i--) sa[c[x[i]]--] = i;
for (int k = 1; k <= n; k <<= 1)
{
int num = 0;
for (int i = n - k + 1; i <= n; i++) y[++num] = i; //以长度为k,i为第一关键字,i+k为第二关键字
for (int i = 1; i <= n; i++)
if (sa[i] > k) y[++num] = sa[i] - k;
//对第二关键字排序
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
if (num == n)break;
m = num;
}
}
void get_height()
{
for (int i = 1; i <= n; i++) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i++) //利用 height[rk[i]]>= height[rk[i-1]]-1
{
if (rk[i] == 1) continue;
if (k) k--;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
unordered_mapmp;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n;
vectorans(n+1);
for(int i=n;i>=1;i--)
{
cin>>s[i];
if(mp[s[i]]==0) mp[s[i]]=++m;
s[i]=mp[s[i]];
}
get_sa();
get_height();
ll res=0;
for(int i=1;i<=n;i++)
{
res+=n-sa[i]+1-height[i];
l[i]=i-1,r[i]=i+1;
}
l[n+1]=n,r[0]=1;
for(int i=1;i<=n;i++) //从前往后删
{
ans[i]=res;
int k=rk[i],nk=r[k];
res-=n-sa[k]+1-height[k];
res-=n-sa[nk]+1-height[nk];
height[nk]=min(height[nk],height[k]);
res+=n-sa[nk]+1-height[nk];
r[l[k]]=r[k],l[r[k]]=l[k];
}
for(int i=n;i>=1;i--)cout< \(H - Can You Solve the Harder Problem?\)
题意:给定一个数组,求所有本质不同的子段的最大值的和
Sol:(后缀数组+单调栈+RMQ)
如果不考虑本质不同的限制,那么就是直接枚举每个数作为左端点,然后利用单调栈找到右边第一个大于这个数的下标,计算贡献即可(可以参考\(Atcoder Minimum Sum\))。考虑限制要怎么操作呢?
定义数组\(nxt[i]\)为第\(i\)个数右边第一个比它大的数的下标。\(suf[i]\)表示从\(i\)开始的依次递增的贡献的后缀和,转移是\(suf[i]=a[i]\times(nxt[i]-i)+suf[nxt[i]]\),什么意思呢,如下图!
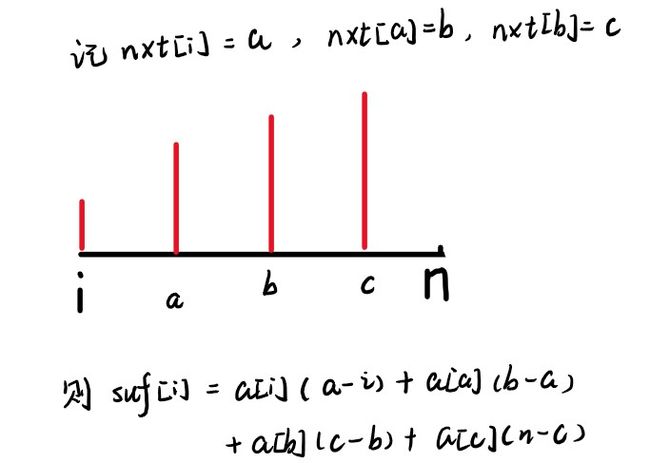
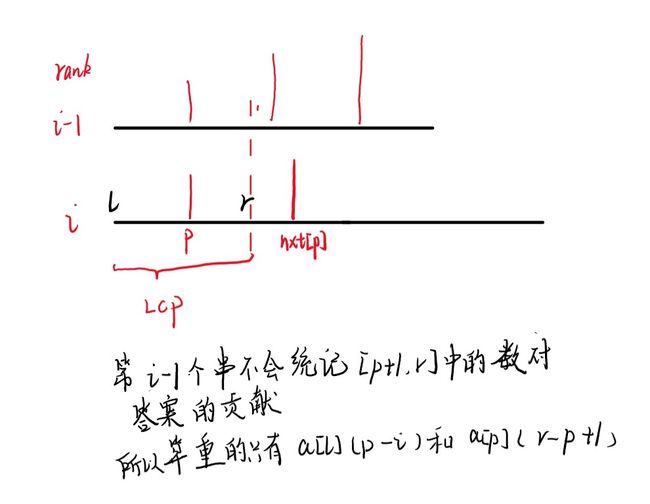
按字典序排好序后,假设当前计算到第\(i\)个串,如果\(height[i]\)不等于,说明第\(i\)个串和第\(i-1\)个串有公共前缀,如果直接加到答案里会算重。设\(l=sa[i],r=sa[i]+height[i]-1\),即区间\([l,r]\)是重复的部分,设\(p\)是\([l,r]\)中值最大的数的下标,则\(nxt[p]\)一定大于\(r\),因为\(a[p]\)是\([l,r]\)中最大的了,而\(a[nxt[p]]>a[p]\),因此\(nxt[p]\)只能存在于比\(r\)大的地方。所以答案贡献就是\(suf[nxt[p]]+a[p]\times (nxt[p]-r-1)\),为什么是\(nxt[p]-r-1\)是因为第\(i-1\)个串已经计算了\([p+1,r]\)对数\(a[p]\)的贡献,可能有人会觉得这样这样子会不会遗漏统计\([r+1,nxt[p-1]]\)对\([p+1,r]\)中的数的贡献,其实不会,为什么,因为我们计算的重复只是和第\(i-1\)个串比较,第\(i-1\)个串是不会统计\([p+1,r]\)中的数对答案的贡献,所以我们在第\(i\)个串不需要考虑这部分。
#include
#define ll long long
using namespace std;
const int N =2e5+10;
int n, m;
int s[N];
int sa[N], x[N], y[N], rk[N], height[N], c[N];
void get_sa()
{
//基数排序o(n)
//先对第一关键字(模式串出现的字母)排序
for(int i=1;i<=n;i++) c[i]=sa[i]=0;
for (int i = 1; i <= n; i++) c[x[i] = s[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i > 0; i--) sa[c[x[i]]--] = i;
for (int k = 1; k <= n; k <<= 1)
{
int num = 0;
for (int i = n - k + 1; i <= n; i++) y[++num] = i; //以长度为k,i为第一关键字,i+k为第二关键字
for (int i = 1; i <= n; i++)
if (sa[i] > k) y[++num] = sa[i] - k;
//对第二关键字排序
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
if (num == n)break;
m = num;
}
}
void get_height()
{
for (int i = 1; i <= n; i++) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i++) //利用 height[rk[i]]>= height[rk[i-1]]-1
{
if (rk[i] == 1) continue;
if (k) k--;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
int f[N][20];
void RMQ_init()
{
for (int i = 1; i <= n+1; i++) f[i][0] = i;
for (int j = 1; j <=18 ; j++)
for (int i = 1; i + (1 << j) - 1 <= n; i++) {
int x = f[i][j - 1], y = f[i + (1 << (j - 1))][j - 1];
f[i][j] = s[x] > s[y] ? x: y; //下标和最大值看情况转换
}
}
int RMQ_query(int l, int r) {
int k = log2(r - l + 1);
int x = f[l][k], y = f[r - (1 << k) + 1][k];
return s[x] > s[y] ? x : y;
}
int nxt[N],stk[N];
ll suf[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin>>T;
while(T--)
{
cin>>n;
for(int i=1;i<=n;i++) nxt[i]=suf[i]=stk[i]=0;
stk[n+1]=0;
vectorv;
for(int i=1;i<=n;i++)
{
cin>>s[i];
v.push_back(s[i]);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
m=v.size();
for(int i=1;i<=n;i++) s[i]=lower_bound(v.begin(),v.end(),s[i])-v.begin()+1;
RMQ_init();
get_sa();
get_height();
int top=1;
s[n+1]=1e6+10,stk[top]=n+1;
for(int i=n;i>=1;i--)
{
while(top&&s[stk[top]]<=s[i]) top--;
stk[++top]=i;
nxt[i]=stk[top-1];
}
nxt[n+1]=n+1;
suf[n+1]=0;
for(int i=n;i>=1;i--) suf[i]=1ll*v[s[i]-1]*(nxt[i]-i);
for(int i=n;i>=1;i--) suf[i]+=suf[nxt[i]];
ll ans=0;
for(int i=1;i<=n;i++)
{
int lcp=height[i];
if(lcp==0) ans+=suf[sa[i]];
else
{
int l=sa[i],r=sa[i]+lcp-1;
int p=RMQ_query(l,r);
ans+=suf[nxt[p]]+1ll*v[s[p]-1]*(nxt[p]-r-1);
}
}
cout< \(Atcoder Minimum Sum\)
题意
给定一个长度为\(N\)的\(1\)到\(N\)的一个排列,让你计算\(\sum_{l=1}^n\sum_{r=l}^nmin(a_l,a_{l+1},...,a_r)\)
\(1\le N\le 200000\)
Sol
考虑统计每一个\(a_i\)作为贡献的区间数量
很容易想到先找到\(a_i\)右边第一个比\(a_i\)小的数的下标\(r[i]\)和左边第一个比\(a_i\)小的数的下标\(l[i]\)。(经典单调栈操作)
比如这样一个序列\(1,4,3,6,9,2,7,8\)
考虑数字\(3\)下标为\(3\)的贡献,则左边第一个比\(3\)小的数的下标为\(1\),则右边第一个比\(3\)小的数的下标为\(6\),那么显然有贡献的区间为\([2,3],[3,3],[3,4],[3,5],[2,4],[2,5]\),由乘法原理知道有\((3-1)\times (6-3)\)个,即\((i-l[i])\times (r[i]-i)\)个。