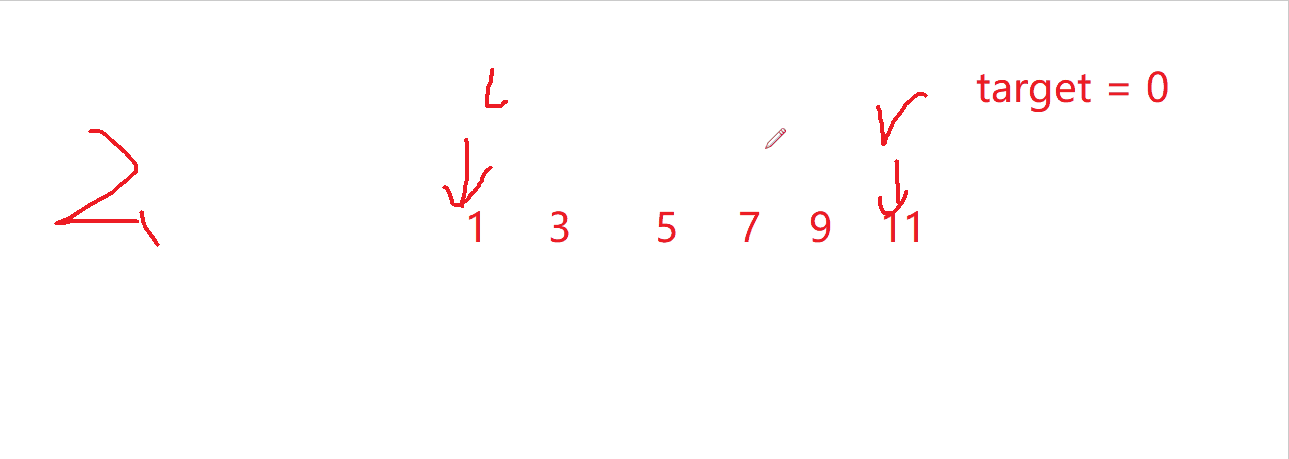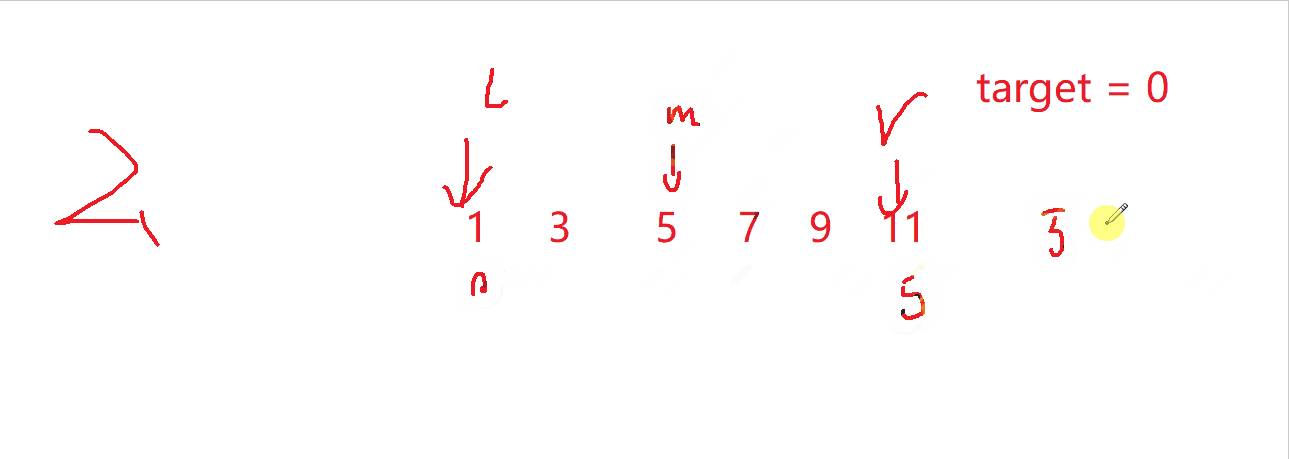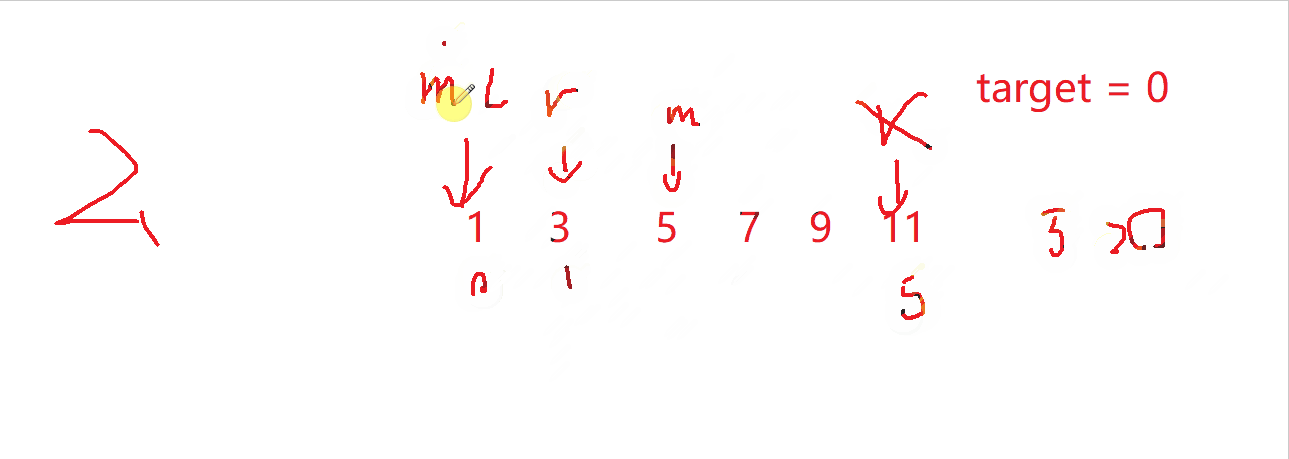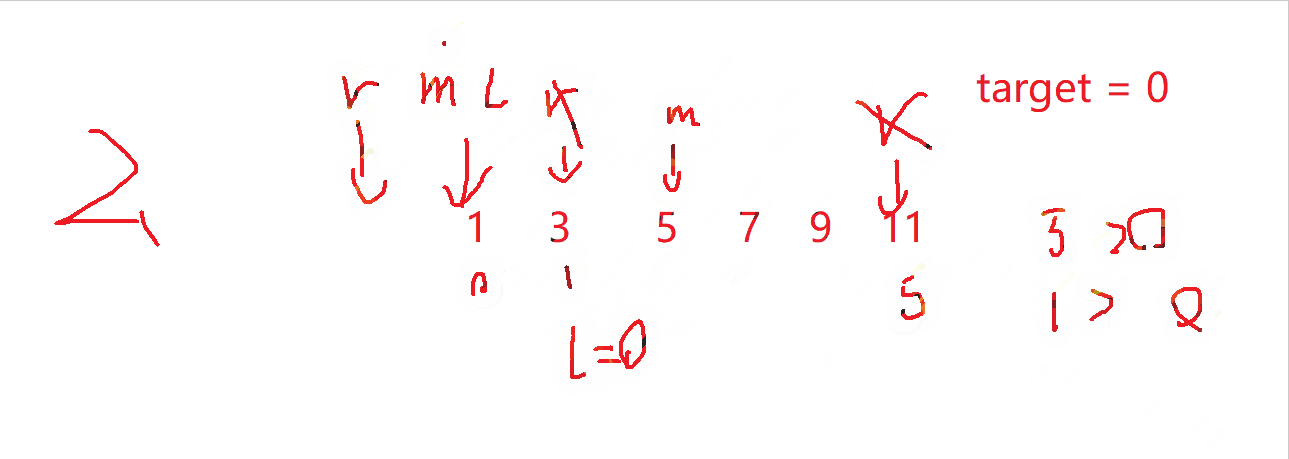【刷题日记】C语言经典编程题
大家好,我是白晨,一个不是很能熬夜,但是也想日更的人✈。如果喜欢这篇文章,点个赞,关注一下白晨吧!你的支持就是我最大的动力!
C语言经典编程题
- 前言
-
- 1.第一个只出现一次的字符
- 2.判断字符是否唯一
- 3.URL化
- 4.字符串压缩
- 5.交换一个数二进制的奇偶位
- 6.递归乘法
- 7.阶乘尾数
- 8.二分查找
- 9.搜索排序旋转数组
- 10.链表内指定区间反转
- 11.从链表中删除总值和为零的连续结点
- 12.链表求和
- 13.括号的最大嵌套深度
- 14.整理字符串
- 15.开幕式烟火
- 16.从根到叶的二进制数之和
- 17.二叉树的坡度
- 18.奇偶树
- 19.数组的相对排序
- 20.将句子排序
- 21.最长和谐子序列
- 后记
前言
锣鼓喧天,鞭炮齐鸣,在这个喜庆的日子里也别忘了学习呀!这几天白晨终于走完亲戚了,可以写点什么以安慰自己放纵的♥了。
所以,我试着总结了一下我在学习C语言阶段遇到的题目,选出了一些经典题目加以解析,希望能让大家在最短的时间内掌握C语言的用法。
下面总结的题目包括了常见题型,入门算法以及数据结构,难度相对来说没有特别难,但是比较经典,第一次见不一定能想到最优的解法,大家可以自己先试着自己挑战一下,再来看解析哟!
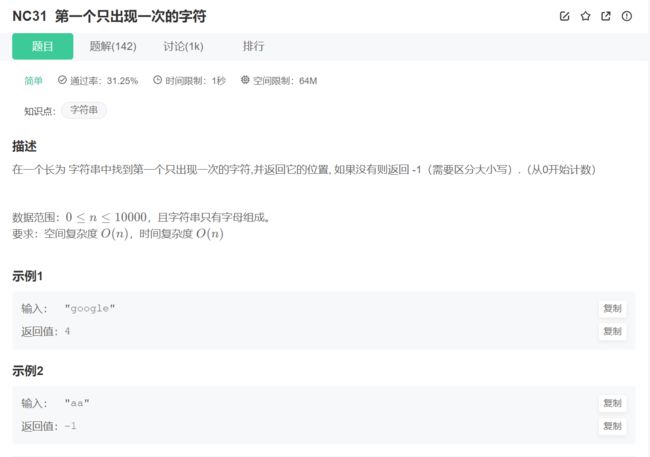
1.第一个只出现一次的字符
int FirstNotRepeatingChar(char* str) {
if (str == NULL)
return -1;
int a[52] = { 0 };
int len = strlen(str);
// 遍历一遍数组,统计个数
for (int i = 0; i < len; i++)
{
if (str[i] >= 'a' && str[i] <= 'z')
{
a[str[i] - 'a']++;
}
else
{
a[str[i] - 'A' + 26]++;
}
}
// 遍历原数组,找出最先出现的单独的数
for (int i = 0; i < len; i++)
{
if (str[i] >= 'a' && str[i] <= 'z')
{
if (a[str[i] - 'a'] == 1)
{
return i;
}
}
else
{
if (a[str[i] - 'A' + 26] == 1)
{
return i;
}
}
}
return -1;
}
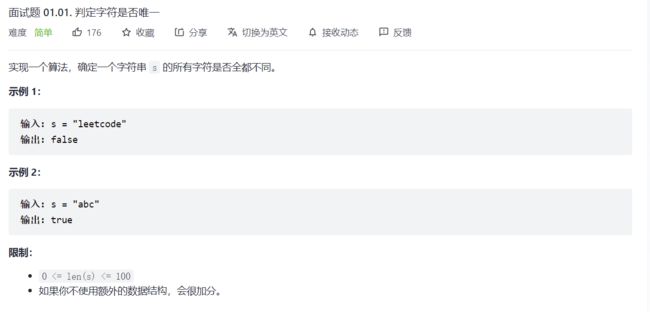
2.判断字符是否唯一
bool isUnique(char* astr) {
if (astr == NULL)
return true;
int a[52] = { 0 };
int len = strlen(astr);
// 遍历一遍数组,统计个数
for (int i = 0; i < len; i++)
{
if (astr[i] >= 'a' && astr[i] <= 'z')
{
a[astr[i] - 'a']++;
}
else
{
a[astr[i] - 'A' + 26]++;
}
}
for (int i = 0; i < len; i++)
{
if (astr[i] >= 'a' && astr[i] <= 'z')
{
if (a[astr[i] - 'a'] >= 2)
{
return false;
}
}
else
{
if (a[astr[i] - 'A' + 26] >= 2)
{
return false;
}
}
}
return true;
}
总结:以上两道题都是判断字符串中字符出现个数的题目,这种题目的普遍思路是
- 先开辟一块空间,运用ASCII码或者数字的相对位置关系,使字符或者数字与空间中的位置一一对应。
- 遍历数组,统计不同字符或数字出现次数。
- 再遍历一遍数组,利用题目限制条件找出答案。
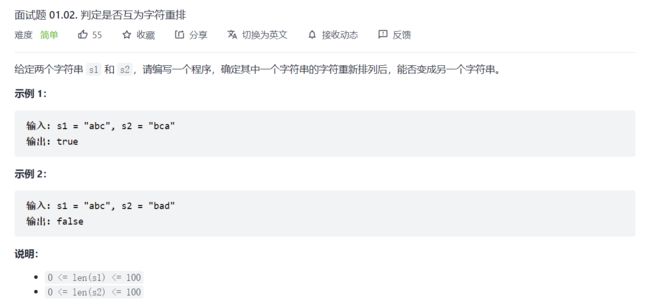
变式1:
bool CheckPermutation(char* s1, char* s2) {
// 先判断两个字符串长度是否相等
int a[52] = { 0 };
int len = strlen(s1);
int len2 = strlen(s2);
if (len != len2)
{
return false;
}
// 遍历一遍数组,统计个数
for (int i = 0; i < len; i++)
{
if (s1[i] >= 'a' && s1[i] <= 'z')
{
a[s1[i] - 'a']++;
}
else
{
a[s1[i] - 'A' + 26]++;
}
}
// 再遍历一遍另一个数组,每遇到一个字母在相应位置--,最后判断a数组的数字是否都为0
for (int i = 0; i < len; i++)
{
if (s2[i] >= 'a' && s2[i] <= 'z')
{
a[s2[i] - 'a']--;
}
else
{
a[s2[i] - 'A' + 26]--;
}
}
for (int i = 0; i < 52; i++)
{
if (a[i] != 0)
{
return false;
}
}
return true;
}
变式2:
bool canPermutePalindrome(char* s) {
int a[128] = { 0 };
int len = strlen(s);
// 遍历一遍数组,统计个数
for (int i = 0; i < len; i++)
{
a[s[i]]++;
}
// 判断一个字符串是否可以组成回文字符串
// 1.字符串中至多有一个只出现一次的字符
// 2.字符串中除了可能出现一次的字符串,其余字符均要出现偶数次
int the_one = 0;// 只能为0或1
for (int i = 0; i < 128; i++)
{
// 当计数为1时,如果the_one为0,则++;如果the_one大于等于0,则已经有出现一次的,返回false
if (a[i] == 1)
{
if (the_one == 0)
{
the_one++;
}
else
{
return false;
}
}
// 当出现大于2次时,如果为偶数,则通过;为奇数,则必须保证the_one 为1
if (a[i] > 2)
{
if (a[i] % 2 == 1)
{
if (the_one == 1)
{
return false;
}
if (the_one == 0)
{
the_one++;
}
}
}
}
return true;
}
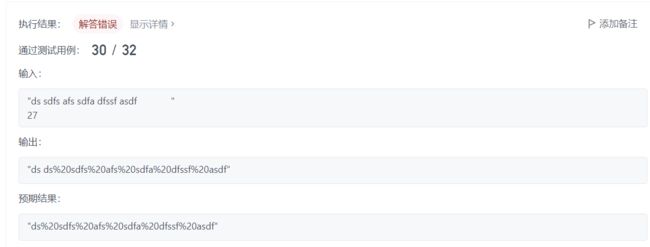
3.URL化
思路:逆序指针法
-
创建两个指针,rend指向真实字符串的最后一个字符,end指向字符串的最后一个字符。eg.示例一中真实字符串的最后一个字符是h,字符串最后一个字符是’ '。
-
两个指针从后往前走,rend如遇到’ ',end倒着输入"%20",否则就将rend指向的值给end。直到rend<字符串的首地址。
-
注意:这个题有个非常坑的点,就是它只告诉你了有足够大的空间放字符串,也没有说到底会不会给多了,如果给多了,那么当rend<字符串的首地址时,end还在字符串中,我们的理想情况情况应该时rend和end一起走向终点。
- 所以我们要进行一定的修正,算出空间到底多出了多少,最后返回时要加上修正值。
具体代码如下:
char* replaceSpaces(char* S, int length) {
if (S == NULL)
return S;
int len = strlen(S);
int gap = len - length;
char* end = S + len - 1, * rend = S + length - 1;
*(end + 1) = 0;
while (rend >= S)
{
if (*rend == ' ')
{
*end-- = '0';
*end-- = '2';
*end-- = '%';
rend--;
gap -= 2;
}
else
*end-- = *rend--;
}
return S + gap;
}
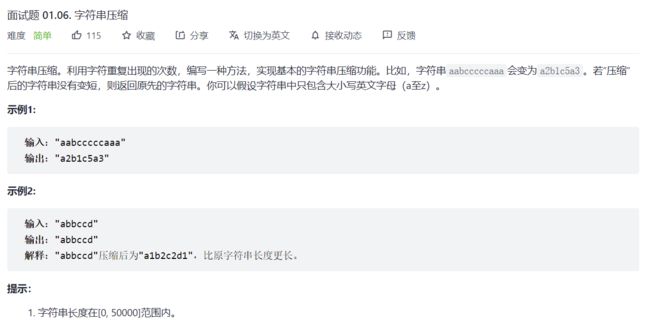
4.字符串压缩
思路:
遍历+统计个数。
char* compressString(char* S) {
int len = strlen(S);
char* begin = S;
char* ret = (char*)calloc(2 * len + 1, 1);
int num = 0;// 开辟的空间的下标
// 当begin不为\0进入循环
while (*begin)
{
// 统计个数
int count = 1;
while (*begin == *(begin + 1))
{
count++;
begin++;
}
ret[num++] = *begin++;
// 将个数转化为字符串
int cnt = 0;
char str[10] = { 0 };
while (count)
{
int nums = count % 10;
str[cnt++] = nums + '0';
count /= 10;
}
while (cnt--)
{
ret[num++] = str[cnt];
}
}
// 别忘了放\0
ret[num] = 0;
// 比较字符串长度
if (len <= num)
{
return S;
}
return ret;
}
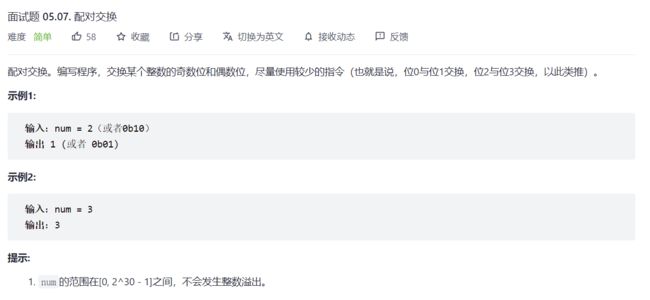
5.交换一个数二进制的奇偶位
int exchangeBits(int num){
return ((0x55555555 & num) << 1) | ((0xaaaaaaaa & num) >> 1);
}
注意:这里的0x55555555和0xaaaaaaaa都是无符号数,所以右移运算的时候会补0。
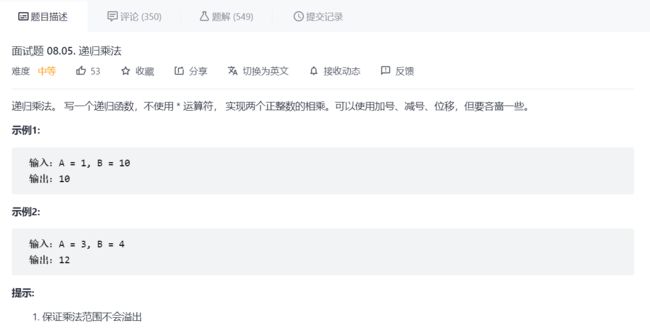
6.递归乘法
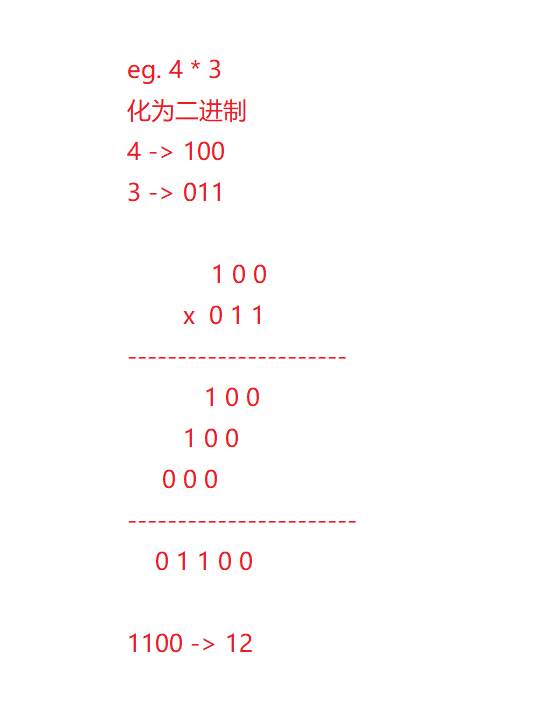
灵感来源:二进制竖式
思路:
有一个数作为竖式下面的数,每次递归向右一位,同时每向右一次,那一层的值(要么为竖式上的数,要么为0)多乘2(向左移一位),直到竖式下的数被左移到值为0。
int multiply(int A, int B)
{
// 思路:二进制乘法竖式
if (B == 0)
{
return 0;
}
// 判断B的第一位是否为1,为一则这一层的值为A,不为1,则这一层值为0,然后递归调用该函数B要往左移一位,并且返回值要乘2(右移一位)
return (B & 1) ? A + (multiply(A, B >> 1) << 1) : (multiply(A, B >> 1) << 1);
}
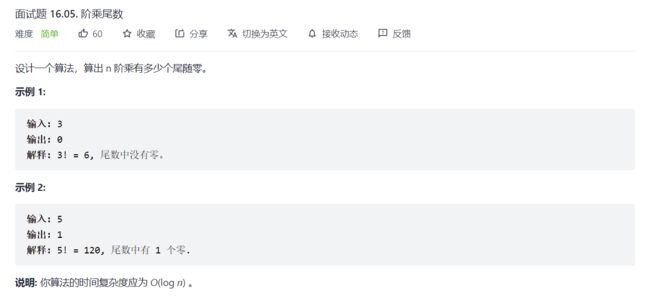
7.阶乘尾数
int trailingZeroes(int n)
{
int cnt = 0;
// 计算阶乘尾数0的关键是统计阶乘中5这个因数的个数
while (n)
{
// 统计5这个因数在n以内出现了多少次,n/5就可得,如n=16,n / 5 = 3,就是5的个数
// 但如果 n = 25,这时 n/5 = 5,仍然大于5,就说明 n 及n以内有25这个因数,25 = 5 * 5,所以前面只算了一次5
// 后面必须再多算一次25因数个数才能算完全,以此类推。
n /= 5;
cnt += n;
}
return cnt;
}
8.二分查找
思想:二分查找
如果要指定插入位置,这里我们可以分三类讨论二分查找:
- 数据插入到数组中间
l = 3,正好为插入位置
- 数据要放到数组头
l = 0,正好也是插入位置
- 数据要放到数组尾
l = 6,也是数据要插入的位置
所以,我们只需要进行二分查找,最后返回l就可以。
int searchInsert(int* nums, int numsSize, int target) {
int left = 0, right = numsSize - 1;
while (left <= right)
{
int avr = (left + right) / 2;
if (nums[avr] == target)
{
return avr;
}
if (nums[avr] > target)
{
right = avr - 1;
}
else
{
left = avr + 1;
}
}
return left;
}
结论:二分查找如果未找到相应的值,那么最后的
left就是数据应该插入的位置
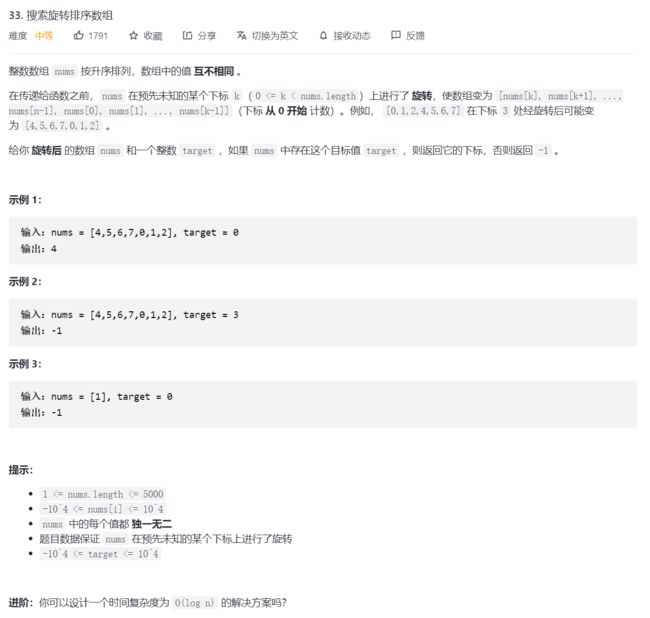
9.搜索排序旋转数组
二分查找的变式,如果要使时间复杂度到 O ( l o g 2 n ) O(log_2~n) O(log2 n),则必须使用二分查找,也即必须找到有序的部分数组。
- 如果中间的数小于最右边的数,则右半段是有序的
- 若中间数大于最右边数,则左半段是有序的
然后,我们要在有序的半段里用首尾两个数组来判断目标值是否在这一区域内:
- 如果在,则就可以在这一段用二分查找
- 不在,则更改界限,在另一半段(假设这一段叫2半段)中查找。但是必须注意,2半段并不是一个有序的半段,这是我们要重复上述找到有序部分数组的过程,更改左右界限,直到找到有序的那一段或者找到目标元素。
int search(int* nums, int numsSize, int target) {
int left = 0;
int right = numsSize - 1;
while (left <= right)
{
int mid = ((left - right) >> 1) + right;
// 依旧采用二分查找的思想
if (nums[mid] == target)
{
return mid;
}
// 当 最左边的数 小于等于 中间的数时,代表 数组的左半部分 是有序的
// 这里是 小于等于 的原因是有特殊情况,eg.[3,1] target = 1
else if (nums[left] <= nums[mid])
{
// 当左半部分有序,并且目标在[left,mid)之间时
if (nums[left] <= target && target < nums[mid])
{
// 右界限缩
right = mid - 1;
}
// 当左半部分有序,并且目标不在[left,mid)之间时
else
{
// 左界限缩
left = mid + 1;
}
}
// 当 最右边的数 大于 中间的数时,代表 数组的左半部分 是有序的
else
{
// 同理当右半部分有序,并且目标在(mid,right]之间时
if (nums[right] >= target && target > nums[mid])
{
left = mid + 1;
}
// 当右半部分有序,并且目标不在(mid,right]之间时
else
{
right = mid - 1;
}
}
}
// 当left > right则为找不到
return -1;
}
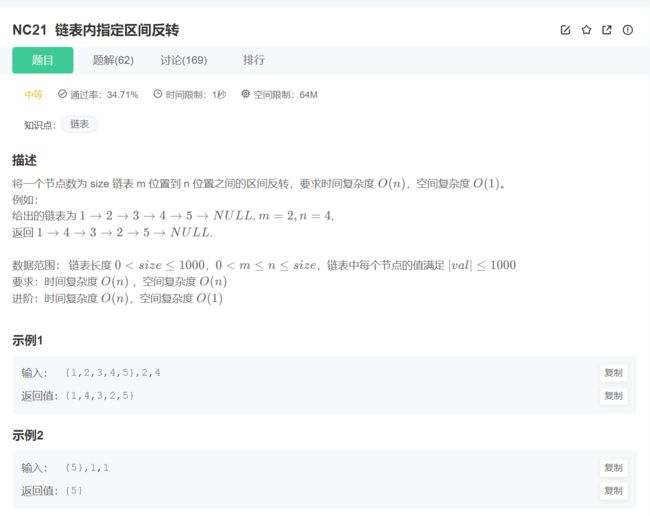
10.链表内指定区间反转
本题是反转链表的一个变式,所以可以采用两种方法:
-
反转指针法
ListNode* reverseBetween(ListNode* head, int m, int n) { // 反转指针法 // 三个指针记录位置 ListNode* cur = head, * next = head->next, * prev = NULL; // 记录反转结束和开始的位置以及开始反转的前驱结点 ListNode* begin, * end, * prevB = NULL; int cnt = 1; // 当next为空,则此中只有一个结点,直接返回即可 if (next == NULL) { return head; } while (cnt <= n) { next = cur->next; // 记录开始反转的前驱结点 if (cnt == m - 1) { prevB = cur; } // 记录反转开始的结点 if (cnt == m) { end = cur; } // 记录反转结束的结点 if (cnt == n) { begin = cur; } // 开始反转 if (cnt >= m) { cur->next = prev; } prev = cur; cur = next; cnt++; } // 开始反转的位置的结点就是反转后m~n中最后一个结点,则这个结点的指针指向第n+1个结点 end->next = next; // 如果m!=1,则有前驱结点,前驱结点指向反转后开始的结点 if (prevB) prevB->next = begin; // 如果m == 1,头结点会改变,所以我们返回改变后的头结点 if (m == 1) { return begin; } return head; } }; -
哨兵位头插法
ListNode* reverseBetween(ListNode* head, int m, int n) { if (head == NULL || head->next == NULL || m == n) return head; // 开辟一个哨兵头节点,这样就可以将后面结点统一处理 ListNode* tmp = (ListNode*)malloc(sizeof(ListNode)); tmp->next = head; // 找到所要反转的结点的前驱结点 ListNode* prev = tmp; for (int i = 1; i < m; i++) { prev = prev->next; } // 开始头插反转 ListNode* cur = prev->next; for (int i = m; i < n; i++) { ListNode* next = cur->next; cur->next = next->next; // 这里的prev->next每一次都会改变为新插入的结点,所以不要直接写成cur next->next = prev->next; prev->next = next; } ListNode* newHead = tmp->next; free(tmp); return newHead; }
这里注意,此处的头插前驱结点prev始终不变,而prev->next始终在变,所以头插始终发生在prev结点之后。
而且这种中间头插比直接在首结点头插多了一步,前驱结点的指向。
11.从链表中删除总值和为零的连续结点
思路:
- 设置哨兵位结点,双重循环,层层遍历
struct ListNode* removeZeroSumSublists(struct ListNode* head)
{
struct ListNode* pre = (struct ListNode*)malloc(sizeof(struct ListNode));
pre->next = head;
struct ListNode* p = pre;
// 保证p始终为要删除对象的前驱结点
while (p)
{
int sum = 0;
struct ListNode* q = p->next;
while (q)
{
sum += q->val;
if (sum == 0)
{
struct ListNode* tmp = p->next;
p->next = q->next;
q = q->next;
while (tmp != q)
{
struct ListNode* ttmp = tmp->next;
free(tmp);
tmp = ttmp;
}
continue;
}
q= q->next;
}
p = p->next;
}
head = pre->next;
free(pre);
return head;
}
这里有个很重要的注意,如果用C++写,则不能直接用free释放结点,不然会导致权限冲突,建议用C语言写,可以释放掉和为0的结点。
如果为C++,这一步可以省略。
12.链表求和
思路:
- 如果两个结点不为空,相加,根据所得结果决定进位
- 其中一个为空,则直接复制另一个结点的值到新结点
- 两个都为空,结束
// 生成对应两个结点两数和的结点,并插入到前驱结点上
void _addTwoNumbers(struct ListNode** prev,int* flag, int sum)
{
struct ListNode* cur = (struct ListNode*)malloc(sizeof(struct ListNode));
cur->next = NULL;
if (sum < 10)
{
cur->val = sum;
*flag = 0;
}
else
{
cur->val = sum % 10;
*flag = 1;
}
(*prev)->next = cur;
*prev = cur;
}
struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l2)
{
// 开辟一个头节点,方便插入
struct ListNode* head = (struct ListNode*)malloc(sizeof(struct ListNode));
// 插入的前驱结点
struct ListNode* prev = head;
// 进位标志,为 0 不进位,为 1 进位
int flag = 0;
// 当两个结点都不为空时,进入循环
while (l1 && l2)
{
int sum = l1->val + l2->val;
if (flag == 1)
{
sum++;
}
_addTwoNumbers(&prev, &flag, sum);
l1 = l1->next;
l2 = l2->next;
}
// 当 l1 不为空
while (l1)
{
if (flag == 1)
{
int sum = l1->val + 1;
_addTwoNumbers(&prev,&flag, sum);
}
else
_addTwoNumbers(&prev,&flag, l1->val);
l1 = l1->next;
}
// 当 l2 不为空
while (l2)
{
if (flag == 1)
{
int sum = l2->val + 1;
_addTwoNumbers(&prev,&flag, sum);
}
else
_addTwoNumbers(&prev,&flag, l2->val);
l2 = l2->next;
}
// 当 l1 和 l2 都为空,并且flag == 1时,说明这是仍有进位,要再开辟一个结点存放
if (!l1 && !l2 && flag == 1)
{
_addTwoNumbers(&prev,&flag, 1);
}
// 返回头节点之后的结点
struct ListNode* tmp = head;
head = head->next;
free(tmp);
return head;
}
13.括号的最大嵌套深度
这道题的题目很吓人,而且如果第一眼看到这题往往都会想复杂。比如:用栈实现,或者是不清楚如何才能找出每个部分的最大嵌套深度。
其实这道题很简单,就是绕了一点。
- 遍历这个字符串,遇到
(计数加一,并且计数的最大值就是最大的嵌套深度。 - 遇到
)计数减一,代表已经走出与其最近的(范围。
int maxDepth(char* s) {
int len = strlen(s);
int max = 0;
int size = 0;
for (int i = 0; i < len; i++)
{
if (s[i] == '(')
{
size++;
max = max > size ? max : size;
}
if (s[i] == ')')
size--;
}
return max;
}
14.整理字符串
这道题与前面有些题非常相似,所以我们可以用几种不同的方法求解。
- 遍历法
思想:
- 遍历字符串,由于字符串中全部都是字母,所以我们可以利用大写字母和小写字母的ASCII码值相差32来判断相邻的字母是否为相互的大小写。
- 遇到相互为大小写的字母,删除这两个字母。
char* makeGood(char* s)
{
int len = strlen(s);
for (int i = 0; i < len; i++)
{
// 无论大小写字母,只需满足其中一个就可以说明相邻字母为相互的大小写字母
if (s[i + 1] + 32 == s[i] || s[i + 1] - 32 == s[i])
{
// 用后面的字母将相互的大小写字母覆盖,并且len减去2
for (int j = i + 2; j <= len; j++)
{
s[j] = s[j + 2];
}
len -= 2;
// 现在需要回到被删除字母的前一个字母,如果i==0,则不向前退(下一次for循环的++与这次--抵消,则i下一次仍为0)
// 如i != 0,需要向前退一个(同理,下一次for循环的++与这次-=2抵消一个,正是向前了一个字母)
if (i != 0)
i -= 2;
else
--i;
}
}
return s;
}
这个方法的优点是不需要开辟额外的空间,但这种方法需要比较强的控制能力,并且时间复杂度为 O ( N 2 ) O(N^2) O(N2),不是特别推荐。
- 模拟栈实现
如果你学过栈结构(点我跳转),那么这个题用栈的特性真的是再好不过了
此种方法时间复杂度 O ( N ) O(N) O(N),空间复杂度 O ( N ) O(N) O(N)。
char* makeGood(char* s) {
int len = strlen(s);
// 用字符串模拟实现栈
char* stack = (char*)malloc(len + 1);
int top = 0;
for (int i = 0; i < len; i++)
{
// 入栈
stack[top++] = s[i];
// 当栈中元素达到两个及以上,并且有相互大小写时,出栈两个元素
if (top > 1 && (stack[top - 2] + 32 == s[i] || stack[top - 2] - 32 == s[i]))
{
top -= 2;
}
}
// 给字符串加上\0
stack[top] = 0;
return stack;
}
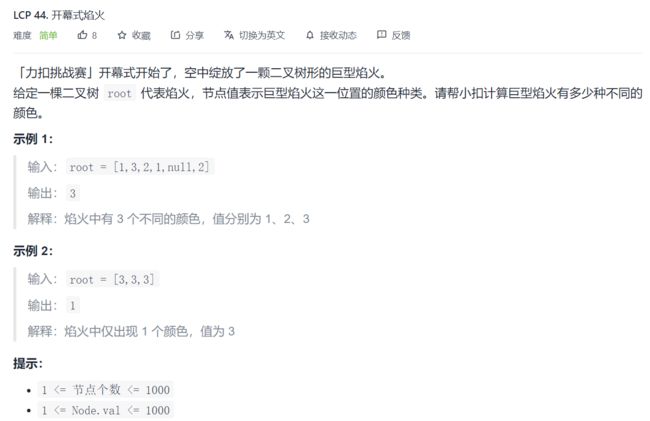
15.开幕式烟火
这个题的思路比较简单,就是统计所有出现的数值,并最后返回出现了多少次不同的数值。
有两种实现方法:
- 记录所有出现的数,遇到未出现过的数就加入数组,遇到出现过的就不加入数组。最后返回数组大小即可
// 最多只可能有1000个不同的值
int a[1000];
// pi是一个输出型参数,主要用来记录数组的大小
void PrevTra(struct TreeNode* root, int* pi)
{
if (root == NULL)
return;
// 默认结点的数是未出现的
int flag = 1;
for (int j = 0; j < *pi; j++)
{
if (a[j] == root->val)
{
// 遍历数组,看有没有出现过
flag = 0;
break;
}
}
// 没出现过就加入数组
if (flag)
{
a[(*pi)++] = root->val;
}
// 先序遍历
PrevTra(root->left, pi);
PrevTra(root->right, pi);
return;
}
int numColor(struct TreeNode* root) {
int i = 0;
PrevTra(root, &i);
// 最后返回数组大小即可
return i;
}
这个方法的时间复杂度较高,主要是遇到一个结点值就必须判断是否出现过,越到后面越慢。
- 哈希数组
对二叉树进行先序遍历,用哈希数组判断当前值是否出现过(出现过就不为0,未出现就是0),每出现一个没有在哈希数组中统计过的元素哈希数组就新增一个值,最后统计哈希数组有多少不为0的值即可。
这个方法适用于结点值取值范围不大时。
// 这里的数组是一个映射,一一映射1~1000的值
int a[1001];
void PrevTra(struct TreeNode* root)
{
if (root)
{
// 在数组的映射位置++
a[root->val]++;
PrevTra(root->left);
PrevTra(root->right);
}
}
int numColor(struct TreeNode* root) {
memset(a, 0, sizeof(a));
PrevTra(root);
int num = 0;
// 统计映射情况
for (int i = 0; i < 1001; i++)
{
if (a[i])
num++;
}
return num;
}
16.从根到叶的二进制数之和
这道题明显是一道通过先序遍历解决的题目,但是这其中的难点是如何才能将所有的值加起来。
我们可以将每次遍历的值记录下来,再通过传参来得到以前的值,每次在以前的值上累加就可以。
具体实现如下:
void _sumRootToLeaf(struct TreeNode* root, int val, int* pSum)
{
// val为记录一条路径上二进制的值
if (root == NULL)
{
return;
}
// val遇到新的结点就得向左一位,再加上新值
val = (val << 1) + root->val;
// 如果这时左右子树都为空,说明一条路径遍历完成,可以将其加到总和中
if (root->left == NULL && root->right == NULL)
{
*pSum += val;
}
// 遍历
_sumRootToLeaf(root->left, val, pSum);
_sumRootToLeaf(root->right, val, pSum);
}
int sumRootToLeaf(struct TreeNode* root) {
int sum = 0;
// sum为输出型参数,最后返回的就是总和
_sumRootToLeaf(root, 0, &sum);
return sum;
}
可以看出,这道题只要时刻能记录下一条路径的值,就可以轻松解答,所以用C++我们也可以利用缺省参数来进行记录。
class Solution {
public:// 默认val为0
int sumRootToLeaf(TreeNode* root, int val = 0) {
if (root == nullptr)
return 0;
val = (val << 1) + root->val;
// 如果左右都为空,说明一条路径结束,返回记录的值;
// 如果不为空,说明未结束,继续遍历,最后返回左右子树每条路径的和
return root->left == root->right ? val
: sumRootToLeaf(root->left, val) + sumRootToLeaf(root->right, val);
}
};
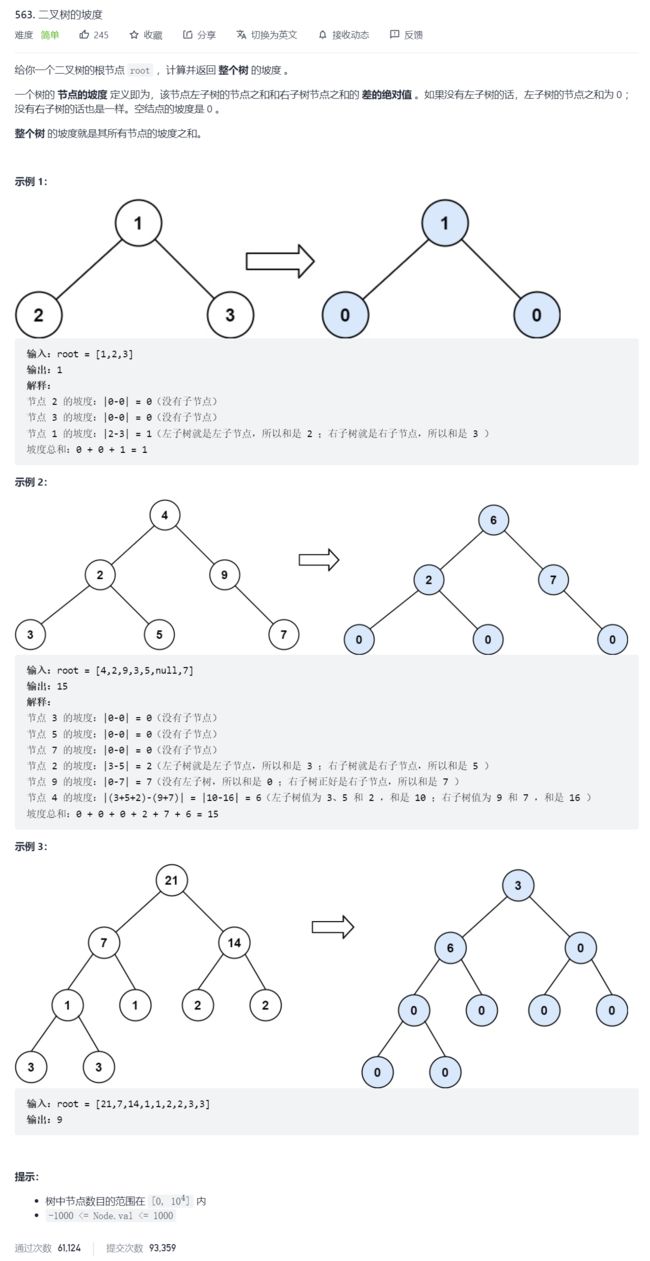
17.二叉树的坡度
这道题其实就是用后序遍历求结点和的变式,只不过多加了一个求坡度的过程,所以也比较简单。
int getSum(struct TreeNode* root)
{
if (root == NULL)
return 0;
return getSum(root->left) + getSum(root->right) + root->val;
}
int findTilt(struct TreeNode* root)
{
if (root == NULL)
return 0;
return findTilt(root->left) + findTilt(root->right) + abs(getSum(root->left) -
getSum(root->right));
}
上面的方式代码短,而且简单易懂,但是它有一个致命的缺点就是每次求一个坡度值,就要调用一次getSum,这样重复调用会极大的浪费时间,所以我们可以将这个代码进行优化。
int _findTilt(struct TreeNode* root, int* ret, int sum)
{
// 为空时,返回0
if (!root)
return 0;
// 求左右子树的高度
int leftsum = _findTilt(root->left, ret, sum);
int rightsum = _findTilt(root->right, ret, sum);
// 求出坡度
int fab = fabs(leftsum - rightsum);
// 输出型参数ret,用来存放各个结点坡度和
*ret += fab;
sum = root->val + leftsum + rightsum;
// 返回结点和
return sum;
}
int findTilt(struct TreeNode* root) {
int sum = 0;
_findTilt(root, &sum, 0);
return sum;
}
每次求出的sum值,是上一个结点的左子树或者右子树结点值的和,我们可以将其返回,这样就少了重复调用的过程。时间复杂度 O ( N ) O(N) O(N),只需要每个结点遍历一次就可以。
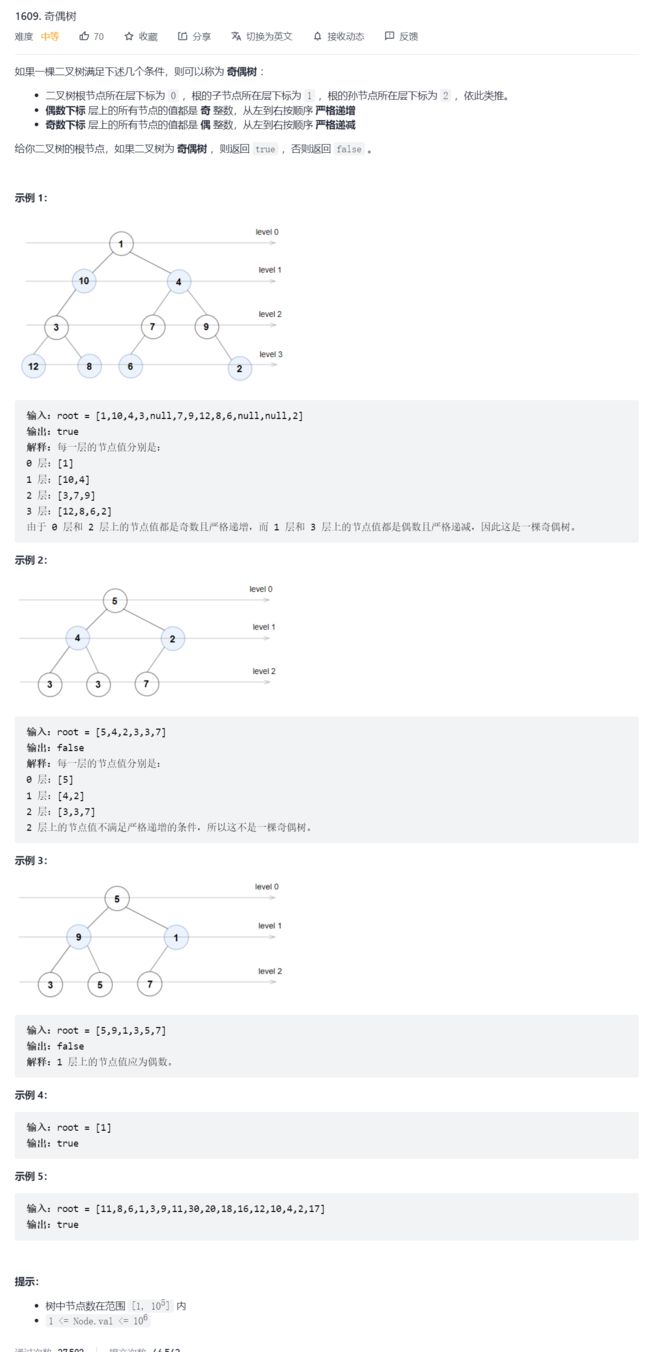
18.奇偶树
这道题的核心逻辑就是:
- 利用队列结构进行层序遍历
所以如何模拟队列结构进行层序遍历就成了首先要攻克的问题。
-
直接使用队列结构
我们可以直接化用以前【数据结构】栈与队列全解析(一篇文章让你从入门到进阶)以及【数据结构】二叉树全解析(入门篇)中的结构上去硬解。(为了避免篇幅过长,队列的结构不多赘述,需要的同学点击上方的链接即可查看)
// 这里我们化用了二叉树的层序遍历代码 bool isEvenOddTree(struct TreeNode* root) { Queue q; QueueInit(&q); QueuePush(&q, root); // begin为下一层首结点 struct TreeNode* begin = root; // i用来判断此节点是否为下一层的首结点 int i = 0; // 记录层数 int layer = -1; // 记录前驱结点的值 int before = 0; while (!QueueEmpty(&q)) { struct TreeNode* tmp = QueueFront(&q); // 如果当前结点与记录中的下一层首结点相同,则更新数据 if (tmp == begin) { i = 0; layer++; // 这里就是保证每一行的第一个结点可以通过下面的判断 // 为奇数层时,使前驱结点的值为整形最大值 if (layer % 2 == 1) before = INT_MAX; // 为偶数层时,使前驱结点的值为整形最小值 if (layer % 2 == 0) before = INT_MIN; } QueuePop(&q); if (layer % 2 == 0) { // 如果为偶数层,出现不为奇数或者是前驱结点的值大于等于当前结点的值,则为假 if (tmp->val % 2 != 1 || before >= tmp->val) { return false; } } else { // 如果为奇数层,出现不为偶数或者是前驱结点的值小于等于当前结点的值,则为假 if (tmp->val % 2 != 0 || before <= tmp->val) { return false; } } // 记录当前结点的值 before = tmp->val; if (tmp->left) { QueuePush(&q, tmp->left); // 如果i为0,说明下一层的第一个结点还没出现,记录下一层第一个结点 if(i == 0) { begin = tmp->left; i = 1; } } if (tmp->right) { QueuePush(&q, tmp->right); // 如果i为0,说明下一层的第一个结点还没出现,记录下一层第一个结点 if(i == 0) { begin = tmp->right; i = 1; } } } QueueDestroy(&q); return true; }
这个方法比较偷懒,但是代码长度也是相当的大,而且由于生搬硬套各种函数,导致这个判断的结构效率比较拉跨,所以比较慢。相对来说,我更推荐第二种写法。
-
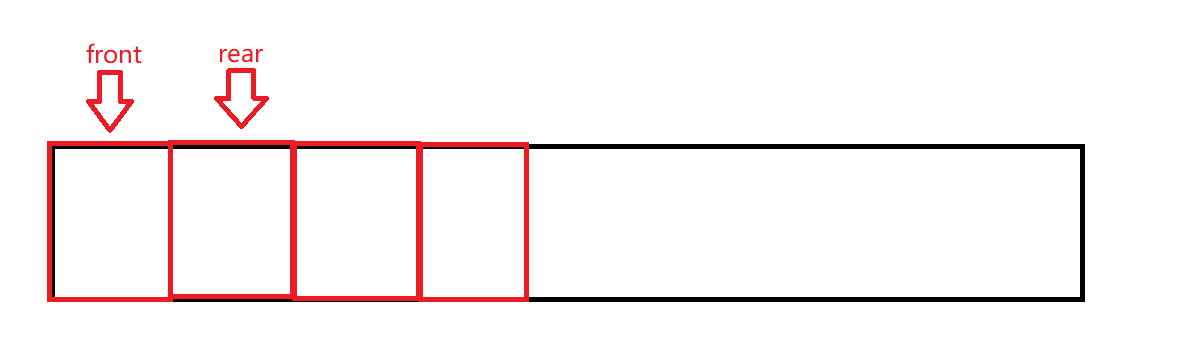
模拟实现队列
这个方法核心是使用数组来模拟实现队列,并且由于数组队列有一些得天独厚的优势,使得代码简洁加高效。
#define N 100002
bool isEvenOddTree(struct TreeNode* root)
{
//申请队列空间,使用数组模拟队列
struct TreeNode* queue[N];
int front = 0;
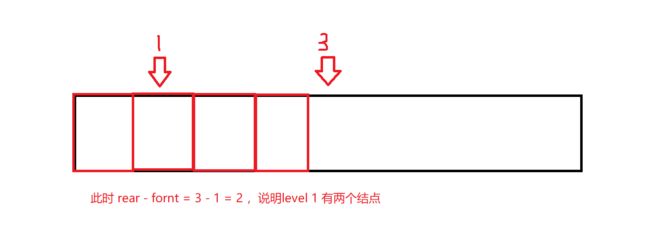
int rear = 0;
int odd = 0; //odd用于判断奇偶层[0:偶数层,1:奇数层]
int pre; //表示当前行判断节点的前驱节点
queue[rear++] = root;
while (front != rear)
{
int cnt = rear - front;
if (odd == 1)
pre = INT_MAX;
if (odd == 0)
pre = INT_MIN;
for (int i = 0; i < cnt; i++)
{
root = queue[front++];
//偶数行判断
if ((odd == 1) && (root->val % 2 != 0 || pre <= root->val))
return false;
//奇数行判断
if ((odd == 0) && (root->val % 2 != 1 || pre >= root->val))
return false;
pre = root->val;
if (root->left)
queue[rear++] = root->left;
if (root->right)
queue[rear++] = root->right;
}
//控制奇偶行标记
odd = (odd + 1) % 2;
}
return true;
}
可以看到数组模拟实现时,有以下几点优势:
- 可以轻松得到每一行有多少个元素,不需要像链式结构一样记录下一层的第一个结点
- 判断结束的条件也简单,直接使用下标判断
- 不需要出队列,直接通过修改下标来改变队头和队尾
19.数组的相对排序
这道题中 arr2 所有的数都在 arr1 出现过,并且 arr2 中数据每一个只出现一次,关键问题就是:如何才能将 arr1 中的 arr2 先单独挑出来排序,再排序剩下的。
核心思路:
- 化用计数排序的思路,先统计 arr1 中每个数字出现的个数(映射到数组的下标上)
- 找到 arr2 和 arr1 都出现的数字
- 找 arr1 有, arr2 没有的数字
int* relativeSortArray(int* arr1, int arr1Size, int* arr2, int arr2Size, int* returnSize) {
int* a = (int*)calloc(1001, sizeof(int));
*returnSize = arr1Size;
// 通过映射位置记录数字出现次数
for (int i = 0; i < arr1Size; i++)
{
a[arr1[i]]++;
}
// j为记录要存放数据的位置,这里我们直接在arr1中存放返回数据,j就为返回数组的下标
int j = 0;
// 将数字按arr2的相对位置放
for (int i = 0; i < arr2Size; i++)
{
while (a[arr2[i]])
{
arr1[j++] = arr2[i];
a[arr2[i]]--;
}
}
// 按升序排列arr2中没有的数字
for (int i = 0; i < 1001; i++)
{
while (a[i]--)
{
arr1[j++] = i;
}
}
return arr1;
}
20.将句子排序
这个题需要将一个个单词分割下来,并按照单词尾的数字排序。
本题的思路不难,但是难在控制上,所以直接上代码讲解:
void strcut(char* s, char a[][30], int* pi)
{
// 记录每个单词的开头
char* head = s;
while (*s)
{
// 遍历s,直到遇到空格或者 \0 停止
while (*s != ' ' && *s != 0)
{
s++;
}
// 记录当前s所指向的字符,可能为空格或者\0
char ch = *s;
// 将单词分割
*s = 0;
// 将单词尾的数字字符转化为整形,也可以直接用 int tmp = *s - '0';
int tmp = atoi(s - 1);
// 将数字位置置为空格,以便于拷贝
*(s - 1) = ' ';
// 记录有多少个单词
(*pi)++;
// 按单词尾数字拷贝到相应的位置
strcpy(a[tmp - 1], head);
if (ch != 0)
{
// 如果没有到s末尾,继续下一个单词
head = s = s + 1;
}
}
}
char* sortSentence(char* s) {
// 用来存放单词
char a[9][30] = { 0 };
int cnt = 0;
strcut(s, a, &cnt);
memset(s,0,strlen(s));
// 追加字符串
for (int i = 0; i < cnt; i++)
{
strcat(s, a[i]);
}
// 在倒数第二个位置,也就是多余空格的位置放上 \0
s[strlen(s) - 1] = 0;
return s;
}
还有一种实现方法,这里简单提一句,感兴趣的小伙伴可以自行去实现:
- 用strtok先将每个单词分割
- 再通过单词末尾数字排序即可
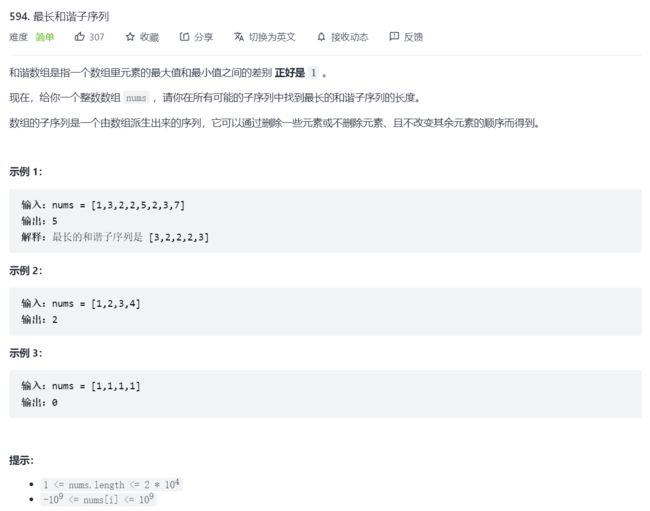
21.最长和谐子序列
这道题的基本思路就是排序+统计最长的和谐子序列,相对来说统计较难实现,我们可以使用双指针法。
int cmp(const void* e1, const void* e2)
{
return *((int*)e1) - *((int*)e2);
}
int findLHS(int* nums, int numsSize) {
// 对数组排升序
qsort(nums, numsSize, sizeof(int), cmp);
int prev = 0;
int num = 0;
// 双指针法,指针 prev 指向 与 i 指向的数字相差为1的数字中第一个数字
for (int i = 1; i < numsSize; i++)
{
// 当两者差大于1时,prev向前移动,直到两者的差小于等于1
while (nums[i] - nums[prev] > 1)
{
prev++;
}
// 当两者差等于1时,记录最长和谐子序列的长度
if (nums[i] - nums[prev] == 1)
{
num = i - prev + 1 > num ? i - prev + 1 : num;
}
}
return num;
}
双指针法非常巧妙,但对于刚入门的同学来说可能比较难想到,也可以使用其他统计方法,大家可以自行探索一下。
后记
这是一个新的系列 ——【刷题日记】,白晨开这个系列的初衷是为了分享一些经典题型,以便于大家更好的学习编程。
如果解析有不对之处还请指正,我会尽快修改,多谢大家的包容。
如果大家喜欢这个系列,还请大家多多支持啦!
如果这篇文章有帮到你,还请给我一个大拇指 和小星星 ⭐️支持一下白晨吧!喜欢白晨【刷题日记】系列的话,不如关注白晨,以便看到最新更新哟!!!