【刷题日记】动态规划经典题目

大家好，我是白晨，一个不是很能熬夜，但是也想日更的人✈。如果喜欢这篇文章，点个赞，关注一下白晨吧！你的支持就是我最大的动力！

前言

---

观前提醒：这篇文章需要一定动态规划的基础

动态规划的方法大多数都非常的抽象，而且在生活中适用的范围也很广。这个算法的抽象性就要求学习动态规划算法时，不能只看算法的思路，而不去做题。

所以，白晨整理了动态规划中非常经典的题目以供大家更好掌握动态规划算法，题目范围从矩阵到字符串等，难度从易到难，抽象程度从一维到二维。

如果你没有接触过动态规划思想 或者 其中有些题目实在想不懂 也没有关系，白晨将在不久后发布动态规划算法的全解析，并在其中在再次着重讲述动态规划中比较难的题目，如背包问题等。

---

动态规划经典题目

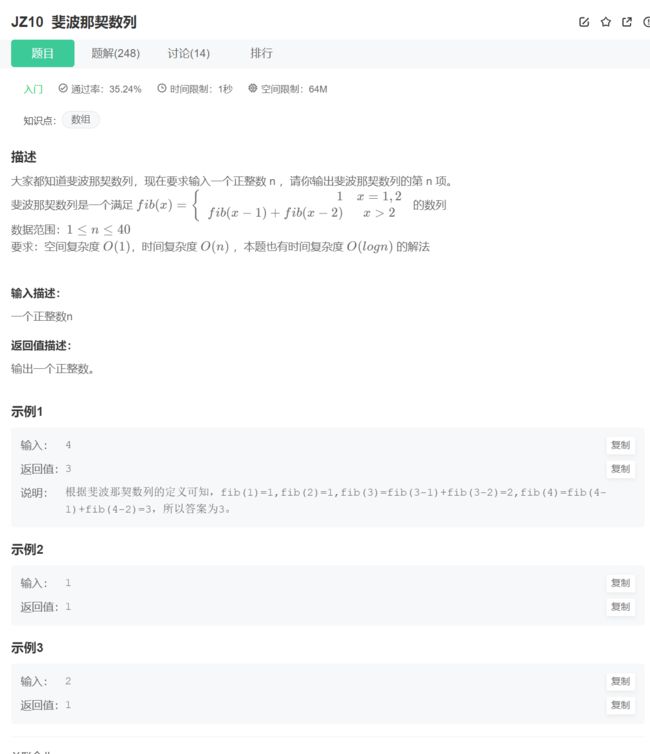
1.斐波那契数列

---

原题链接：斐波那契数列

这道题可能是一道大家刚学C语言的时候就做过的一道题，我们现在按照动态规划的思想来分析一下这道题：

1. 这道题的状态是什么？

   也就是我们需要解决/面对什么，这里我们需要解决的是斐波那契数列第n项的数值，所以我们设第n项数值为 $f(n)$ ,也即状态为 $f(n)$

2. 状态转移方程是什么？

   这里我们可以分析状态，采用 我要从哪里来 的思路，可以轻松得到 $f(n)=f(n-1)+f(n-2)$ 。

3. 状态的初始化是什么？

   也就是一开始的状态是什么？

   $f(1)=1,f(2)=1$

4. 返回值

   由上面就可以得到返回值就为 $f(n)$ 。

总结一下：

• 状态：$f(k)$
• 状态递推：$f(k)=f(k-1)+f(k-2)$
• 初始值：$f(1)=f(2)=1$
• 返回结果：$f(n)$

根据上述分析得到具体代码：

class Solution {
public:
    int Fibonacci(int n) {
        int fib1 = 1;
        int fib2 = 1;
        int f;

        if (n == 1 || n == 2)
            return 1;

        for (int i = 3; i <= n; i++)
        {
            f = fib1 + fib2;

            fib2 = fib1;
            fib1 = f;
        }

        return f;
    }
};

---

2.拆分词句

---

原题链接：拆分词句

状态：
子状态：前1，2，3，…,n个字符能否根据词典中的词被成功分词

• $F(i)$ : 前 i 个字符能否根据词典中的词被成功分词

状态递推：

• $F(i)$: true{$j < i $ && $F(j)$ && $substr[j+1,i]$ 能在词典中找到} OR false
• 在j小于i中，只要能找到一个$F(j)$为true，并且从 j+1到 i 之间的字符能在词典中找到，则 $F(i)$ 为true

初始值：

• 对于初始值无法确定的，可以引入一个不代表实际意义的空状态，作为状态的起始；
• 空状态的值需要保证状态递推可以正确且顺利的进行，到底取什么值可以通过简单的例子进行验证
• $F(0)=true$

返回结果： $F(n)$

class Solution {
public:
    bool wordBreak(string s, unordered_set<string>& dict) {
        if (s.empty())
            return false;
        if (dict.empty())
            return false;

        vector<bool> can_spe(s.size() + 1, false);
        // 初始化
        can_spe[0] = true;

        for (int i = 1; i <= s.size(); i++)
        {
            for (int j = i - 1; j >= 0; j--)
            {
                // 当前 j 个字符能从字典中分割，并且 [j + 1, i] 的字符正好为字典中的字符时
                // 判断为真
                if (can_spe[j] && dict.find(s.substr(j, i - j)) != dict.end())
                {
                    can_spe[i] = true;
                    break;
                }
            }
        }

        return can_spe[s.size()];
    }
};

---

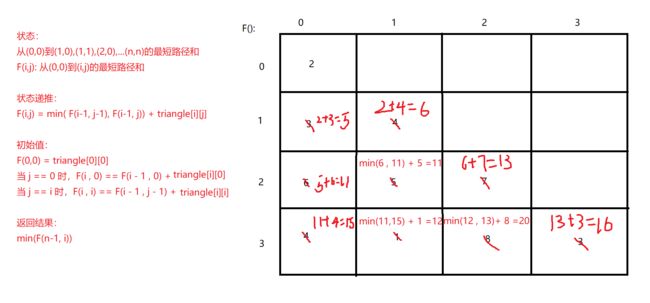
3.三角矩阵

---

原题链接：三角形

class Solution {
public:
    int minimumTotal(vector<vector<int> >& triangle) {
        if (triangle.empty())
            return 0;

        int row = triangle.size();

        for (int i = 1; i < row; i++)
        {
            for (int j = 0; j <= i; j++)
            {
                // 初始化
                if (j == 0)
                    triangle[i][0] = triangle[i - 1][0] + triangle[i][0];
                else if (j == i)
                    triangle[i][j] = triangle[i - 1][j - 1] + triangle[i][j];
                // 选出到达 [i][j] 的最小值
                else
                    triangle[i][j] = min(triangle[i - 1][j], triangle[i - 1][j - 1]) + triangle[i][j];
            }
        }
		
        int Min = triangle[row - 1][0];
		// 遍历最后一行，选出最小值
        for (int j = 1; j < row; j++)
            Min = min(Min, triangle[row - 1][j]);

        return Min;
    }
};

---

4.求路径

---

原题链接：求路径

法一：递归

class Solution {
public:

    int uniquePaths(int m, int n) {
        if (m == 1 || n == 1)
            return 1;

        return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
    }
};

法二：动态规划

class Solution {
public:

    int uniquePaths(int m, int n) {
        if (m == 1 || n == 1)
            return 1;
        // 初始化为1
        vector<vector<int> > a(m, vector<int>(n, 1));


        for (int i = 1; i < m; i++)
        {
            // 到达 [i][j] 的路径数 等于 到达[i - 1][j]和到达[i][j - 1]的路径数之和
            for (int j = 1; j < n; j++)
                a[i][j] = a[i][j - 1] + a[i - 1][j];
        }

        return a[m - 1][n - 1];
    }
};

法三：公式法

class Solution {
public:
    
    int uniquePaths(int m, int n) {
        long long ret = 1;

        for (int i = n, j = 1; j < m; i++, j++)
            ret = ret * i / j;

        return ret;
    }
};

---

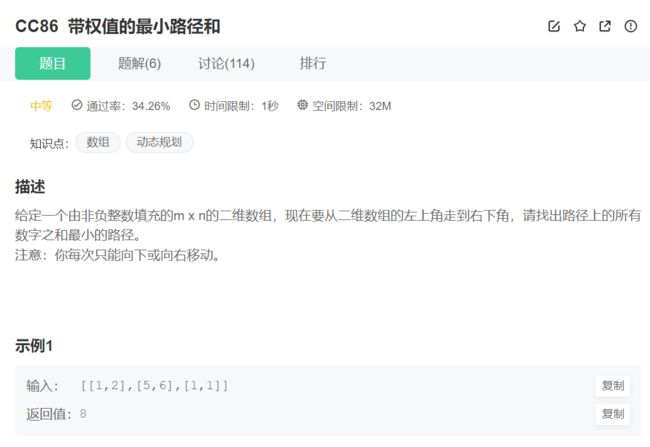
5.带权值的最小路径和

---

原题链接：带权值的最小路径和

class Solution {
public:
    int minPathSum(vector<vector<int> >& grid) {
        int m = grid.size();
        int n = grid[0].size();
		
        //初始化
        for (int i = 1; i < m; i++)
            grid[i][0] = grid[i - 1][0] + grid[i][0];

        for (int i = 1; i < n; i++)
            grid[0][i] = grid[0][i - 1] + grid[0][i];
		
        // 转移方程
        for (int i = 1; i < m; i++)
        {
            for (int j = 1; j < n; j++)
                grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
        }

        return grid[m - 1][n - 1];
    }
};

---

6.背包问题

---

原题链接：背包问题

class Solution {
public:
    int backPackII(int m, vector<int>& A, vector<int>& V) {
        if (A.empty() || V.empty() || m < 1)
            return 0;

        const int N = A.size() + 1;
        const int M = m + 1;
        vector<vector<int> > ret;
        ret.resize(N);
		// 初始化
        for (int i = 0; i != N; ++i) {
            ret[i].resize(M, 0);
        }

        for (int i = 1; i < N; i++)
        {
            for (int j = 1; j < M; j++)
            {
                // 如果背包总空间都不够放第i个物品，则放 i 个物品和 放 i - 1 个物品的情况相同
                if (j < A[i - 1])
                    ret[i][j] = ret[i - 1][j];
                // 如果空间足够放第i个物品，则要判断是否要放入，详见上文解析
                else
                    ret[i][j] = max(ret[i - 1][j], ret[i - 1][j - A[i - 1]] + V[i - 1]);
            }
        }

        return ret[N - 1][m];
    }
};

优化算法：

class Solution {
public:
    int backPackII(int m, vector<int>& A, vector<int>& V) {
        if (A.empty() || V.empty() || m < 1)
            return 0;

        const int M = m + 1; // 包容量
        const int N = A.size() + 1; // 物品数量
        vector<int> ret(M, 0);

        for (int i = 1; i < N; i++)
        {
            // 上面的算法在计算第i行元素时，只用到第i-1行的元素，所以二维的空间可以优化为一维空间
            // 但是如果是一维向量，需要从后向前计算，因为后面的元素更新需要依靠前面的元素未更新（模拟二维矩阵的上一行的值）
            // 并且我们观察到，本行的元素只需要用到上一行的元素，所以从前往后，从后往前都相同
            // 且用到上一行元素的下标不会超过本行元素的下标
            for (int j = m; j >= 0; j--)
            {
                if (j >= A[i - 1])
                    ret[j] = max(ret[j], ret[j - A[i - 1]] + V[i - 1]);
            }
        }

        return ret[m];
    }
};

---

7.分割回文串

---

原题链接：分割回文串

状态：
子状态：到第1,2,3,…,n个字符需要的最小分割数

• $F(i)$: 到第i个字符需要的最小分割数

状态递推：

• $F(i)=minF(i),1+F(j)$, where j < i && j + 1到i是回文串
• 上式表示如果从 j+1 到 i 判断为回文字符串，且已经知道从第1个字符到第 j 个字符的最小切割数，那么只需要再切一次，就可以保证1–>j, j+1–>i都为回文串。

初始化：

• $F(i)=i-1$
• 上式表示到第i个字符需要的最大分割数，比如单个字符只需要切0次，因为单子符都为回文串，2个字符最大需要1次，3个2次…

返回结果：

• $F(n)$

class Solution {
public:
    // 判断是否为回文字符串
    bool isPal(string& s, int left, int right)
    {
        while (left < right)
        {
            if (s[left] != s[right])
                return false;
            left++;
            right--;
        }

        return true;
    }
    int minCut(string s) {
        if (s.empty())
            return 0;
        int len = s.size();
        int* ret = new int[len + 1];
        // 一个长为 i 的字符串，形成回文字符串，最多要被切 i - 1刀
        for (int i = 0; i <= len; ++i)
        {
            // 初始化为每个字符串最多可能被分割的次数
            ret[i] = i - 1;
        }

        for (int i = 2; i <= len; ++i)
        {
            for (int j = 0; j <= i; j++)
            {
                // 判断 j + 1 到 i 的字符串是否为回文字符串
                if (isPal(s, j, i - 1))
                    ret[i] = min(ret[i], ret[j] + 1);
            }
        }

        return ret[len];
    }
};

上述方法两次循环时间复杂度是 $O(n^2)$ ，判断回文串时间复杂度是 $O(n)$ ，所以总时间复杂度为 $O(n^3)$ 。

对于过长的字符串，在OJ的时候会出现TLE(Time Limit Exceeded)，判断回文串的方法可以继续优化，使总体时间复杂度将为 $O(n^2)$ 。

判断回文串，这是一个“是不是”的问题，所以也可以用动态规划来实现

状态：
子状态：从第一个字符到第二个字符是不是回文串，第1-3，第2-5，…

• $F(i,j)$: 字符区间 [i,j] 是否为回文串

状态递推：

• $F(i,j)$: true->{$s[i]==s[j]$ && $F(i+1,j-1)$} OR false
  上式表示如果字符区间首尾字符相同且在去掉区间首尾字符后字符区间仍为回文串，则原字符区间为回文串
• 从递推公式中可以看到第 i 处需要用到第 i + 1 处的信息，所以 i 应该从字符串末尾遍历

初始化：
$F(i,j)$ = false

返回结果：
矩阵$F(n,n)$, 只更新一半值（i <= j），$n^2 / 2 $

class Solution {
public:
    vector<vector<bool> > getMat(string& s)
    {
        int len = s.size();
        vector<vector<bool> > mat = vector<vector<bool> >(len, vector<bool>(len, false));

        for (int i = len - 1; i >= 0; --i)
        {
            // 判断[i , j]范围内是否为回文
            for (int j = i; j < len; ++j)
            {
                if (j == i)
                    mat[i][j] = true;
                else if (j == i + 1)
                    mat[i][j] = (s[i] == s[j]);
                else
                    mat[i][j] = ((s[i] == s[j]) && mat[i + 1][j - 1]);
            }
        }
        return mat;
    }


    int minCut(string s) {
        if (s.empty())
            return 0;
        int len = s.size();
        int* ret = new int[len + 1];
        // 获取回文字符串判断数组
        vector<vector<bool> > mat = getMat(s);
        // 一个长为 i 的字符串，形成回文字符串，最多要被切 i - 1刀
        for (int i = 0; i <= len; ++i)
        {
            ret[i] = i - 1;
        }

        for (int i = 2; i <= len; ++i)
        {
            for (int j = 0; j <= i; ++j)
            {
                // 此时判断 j + 1 到 i 的字符串是否为回文字符串，就可以直接从数组中拿
                if (mat[j][i - 1])
                    ret[i] = min(ret[i], ret[j] + 1);
            }
        }

        return ret[len];
    }
};

综上，这个算法的时间复杂度被优化到了 $O(n^2)$

---

8.编辑距离

---

原题链接：编辑距离

状态：

word1 的前 1，2，3，...m 个字符转换成 word2 的前 1，2，3，...n 个字符需要的编辑距离

• $F(i,j)$: word1 的前 i 个字符于 word2 的前 j 个字符的编辑距离

状态递推：

• $F(i,j)=minF(i-1,j）+1,F(i,j-1)+1,F(i-1,j-1)+(w1[i]==w2[j]?0:1)$

上式表示从删除，增加和替换操作中选择一个最小操作数

• $F(i-1,j)$: $w1[1,...,i-1]$ 于 $w2[1,...,j]$ 的编辑距离，删除 $w1[i]$ 的字符—> $F(i,j)$
• $F(i,j-1)$: $w1[1,...,i]$ 于 $w2[1,...,j-1]$ 的编辑距离，增加一个字符—> $F(i,j)$
• $F(i-1,j-1)$: $w1[1,...,i-1]$ 于 $w2[1,...,j-1]$ 的编辑距离，如果 $w1[i]$ 与 $w2[j]$ 相同，不做任何操作，编辑距离不变，如果 $w1[i]$ 与 $w2[j]$ 不同，替换 $w1[i]$ 的字符为 $w2[j]$—> $F(i,j)$

初始化：
初始化一定要是确定的值，如果这里加入空字符串，以便于确定初始化状态

• $F(i,0)=i$ :word与空串的编辑距离，删除操作
• $F(0,i)=i$ :空串与word的编辑距离，增加操作

返回结果：$F(m,n)$

class Solution {
public:
    int minDistance(string word1, string word2) {
        if (word1.empty() || word2.empty())
            return max(word1.size(), word2.size());

        int len1 = word1.size();
        int len2 = word2.size();
        vector<vector<int>> ret(len1 + 1, vector<int>(len2 + 1, 0));

        // 初始化
        // j == 0 时
        for (int i = 0; i <= len1; ++i)
            ret[i][0] = i;
        // i == 0 时
        for (int i = 0; i <= len2; ++i)
            ret[0][i] = i;

        for (int i = 1; i <= len1; ++i)
        {
            for (int j = 1; j <= len2; ++j)
            {
                // 先选择删除 or 插入
                ret[i][j] = min(ret[i - 1][j] + 1, ret[i][j - 1] + 1);
				
                // 判断是否要替换，如果要替换，操作数 +1 ，反之不变
                // word1的第 i 个字符，对应索引为i - 1，word2同理
                if (word1[i - 1] == word2[j - 1])
                    ret[i][j] = min(ret[i - 1][j - 1], ret[i][j]);
                else
                    ret[i][j] = min(ret[i - 1][j - 1] + 1, ret[i][j]);
            }
        }

        return ret[len1][len2];
    }
};

---

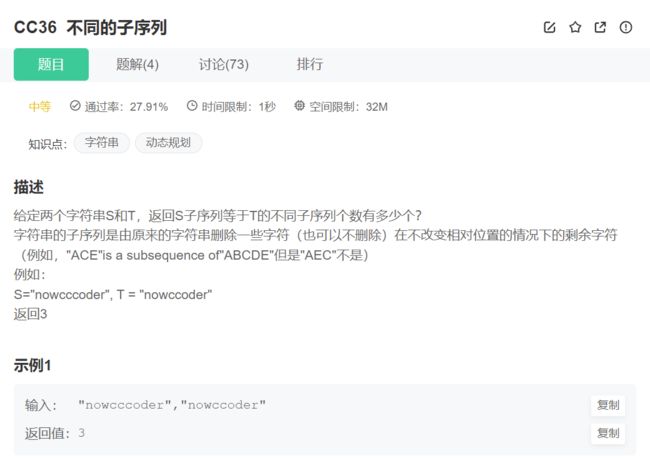
9.不同子序列

---

原题链接：不同的子序列

状态：
子状态：由 S 的前 1,2,...,m 个字符组成的子串与 T 的前 1,2,...,n 个字符相同的个数

• $F(i,j)$ : S[0 ~ i-1] 中的子串与 T[0 ~ j-1] 相同的个数

状态递推：
在 $F(i,j)$ 处需要考虑 $S[i-1]=T[j-1]$ 和 $S[i-1]!=T[j-1]$两种情况（这里S的第i个字符索引值就是 i - 1 , T同理）

• 当$S[i-1]=T[j-1]$:
  1. 让$S[i-1]$匹配$T[j-1]$，则
     $F(i,j)=F(i-1,j-1)$
  2. 让$S[i-1]$不匹配$T[j-1]$,则问题就变为 S[0 ~ i-1] 中的子串与 T[0 ~ j-1] 相同的个数，则
     $F(i,j)=F(i-1,j)$
     故，$S[i-1]=T[j-1]$时，$F(i,j)=F(i-1,j-1)+F(i-1,j)$
• 当$S[i-1]!=T[j-1]$:
  问题退化为 S[0 ~ i-2] 中的子串与 T[0 ~ j-1] 相同的个数
  故，$S[i-1]!=T[j-1]$时，$F(i,j)=F(i-1,j)$

初始化：引入空串进行初始化

• $F(i,0)=1$ —> S的子串与空串相同的个数，只有空串与空串相同

返回结果：
$F(m,n)$

class Solution {
public:
    int numDistinct(string S, string T) {
        int lenS = S.size();
        int lenT = T.size();

        vector<vector<int> > ret(lenS + 1, vector<int>(lenT + 1, 0));
        // 初始化
        for (int i = 0; i <= lenS; ++i)
            ret[i][0] = 1;

        for (int i = 1; i <= lenS; ++i)
        {
            for (int j = 1; j <= lenT; ++j)
            {
                // 判断S的第i个字符是否与T的第j个字符相等
                // 如相等，可以选择是否使用S的第i个字符，最后结果为 使用S的第i个字符的情况 + 未使用S的第i个字符的情况
                // 不相等的话，就继承 S的前i - 1个字符 与 T的前j个字符 相同的个数
                if (S[i - 1] == T[j - 1])
                    ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
                else
                    ret[i][j] = ret[i - 1][j];
            }
        }


        return ret[lenS][lenT];
    }
};

我们观察发现 $ret[i,j]$ 的取值只与 $ret[i-1,j]$ 和 $ret[i-1,j-1]$ 有关，所以我们可以使用与背包问题类似的优化方法，将空间复杂度优化到 $O(n)$ 。

优化算法：

class Solution {
public:
    int numDistinct(string S, string T) {
        int lenS = S.size();
        int lenT = T.size();
        
		// 只保留列就可以
        vector<int> ret(lenT + 1, 0);

        ret[0] = 1;

        for (int i = 1; i <= lenS; ++i)
        {
            // 为了防止上一行的值还没使用就被覆盖，我们必须反着走，从最后一列到第一列
            for (int j = lenT; j >= 1; --j)
            {
                if (S[i - 1] == T[j - 1])
                    ret[j] = ret[j] + ret[j - 1];
                else
                    ret[j] = ret[j];
            }
        }

        return ret[lenT];
    }
};

---

总结

---

• 动态规划状态定义

  • 状态来源：从问题中抽象状态

  • 抽象状态：每一个状态对应一个子问题

  • 状态的定义可以有很多种，但是如果验证状态定义的合理性呢？

    1. 某一个状态的解或者多个状态处理之后的解能否对应最终问题的解。
    2. 状态之间可以形成递推关系。

  • 一维状态 or 二维状态？

    依据题目对象找线索。

    首先尝试一维状态，一维状态不合理时，再定义二维状态。

  • 常见问题的状态：

    • 字符串：状态一般对应子串，状态中每次一般增加一个新的字符。
    • 矩阵：二维状态（在只用到上一行的数据时，可能可以被优化成一维状态）

注意：动态规划中，最重要的一步就是状态的定义，如果状态定义不合理，会带来很多麻烦。

---

这是一个新的系列 ——【刷题日记】，白晨开这个系列的初衷是为了分享一些经典题型，以便于大家更好的学习编程。

如果解析有不对之处还请指正，我会尽快修改，多谢大家的包容。

如果大家喜欢这个系列，还请大家多多支持啦！

如果这篇文章有帮到你，还请给我一个大拇指 和小星星 ⭐️支持一下白晨吧！喜欢白晨【刷题日记】系列的话，不如关注白晨，以便看到最新更新哟！！！

我是不太能熬夜的白晨，我们下篇文章见。