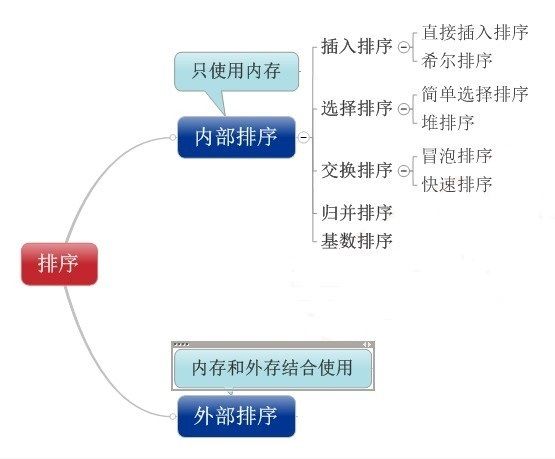
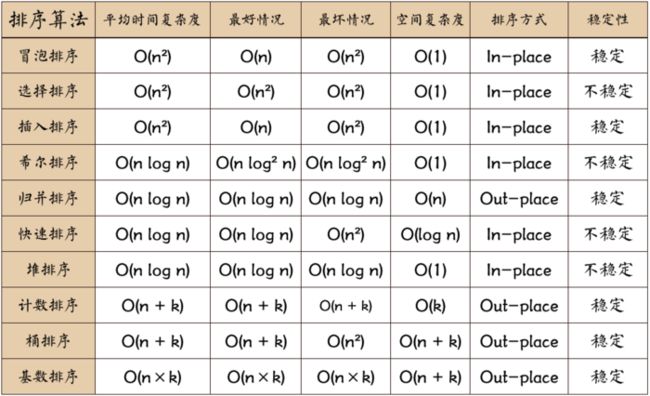
名词解释:
n:数据规模
k:“桶”的个数
In-place:占用常数内存,不占用额外内存
Out-place:占用额外内存
稳定性:排序后2个相等键值的顺序和排序之前它们的顺序相同
冒泡排序(Bubble Sort)
冒泡排序每次找出一个最大的元素,因此需要遍历 n-1 次。还有一种优化算法,就是立一个flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用。
什么时候最快(Best Cases):
当输入的数据已经是正序时。
什么时候最慢(Worst Cases):
当输入的数据是反序时。
def bubbleSort(nums):
# 遍历 len(nums)-1 次
for i in range(len(nums) - 1):
# 已排好序的部分不用再次遍历
for j in range(len(nums) - i - 1):
if nums[j] > nums[j+1]:
# Python 交换两个数不用中间变量
nums[j], nums[j+1] = nums[j+1], nums[j]
return nums
选择排序(Selection Sort)
选择排序须知:
选择排序不受输入数据的影响,即在任何情况下时间复杂度不变。选择排序每次选出最小的元素,因此需要遍历 n-1 次。
def selectionSort(nums):
# 遍历 len(nums)-1 次
for i in range(len(nums) - 1):
minIndex = i
for j in range(i + 1, len(nums)):
# 更新最小值索引
if nums[j] < nums[minIndex]:
minIndex = j
# 把最小数交换到前面
nums[i], nums[minIndex] = nums[minIndex], nums[i]
return nums
插入排序(Insertion Sort)
插入排序须知:
插入排序如同打扑克一样,每次将后面的牌插到前面已经排好序的牌中。插入排序有一种优化算法,叫做拆半插入。因为前面是局部排好的序列,因此可以用折半查找的方法将牌插入到正确的位置,而不是从后往前一一比对。折半查找只是减少了比较次数,但是元素的移动次数不变,所以时间复杂度仍为 O(n^2) !
def insertionSort(nums):
# 遍历 len(nums)-1 次
for i in range(len(nums) - 1):
# curNum 保存当前待插入的数
curNum, preIndex = nums[i+1], i
# 将比 curNum 大的元素向后移动
while preIndex >= 0 and curNum < nums[preIndex]:
nums[preIndex + 1] = nums[preIndex]
preIndex -= 1
# 待插入的数的正确位置
nums[preIndex + 1] = curNum
return nums
快速排序(Quick Sort)
快速排序须知:
又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。它是处理大数据最快的排序算法之一,虽然 Worst Case 的时间复杂度达到了 O(n²),但是在大多数情况下都比平均时间复杂度为 O(n log n) 的排序算法表现要更好,因为 O(n log n) 记号中隐含的常数因子很小,而且快速排序的内循环比大多数排序算法都要短小,这意味着它无论是在理论上还是在实际中都要更快,比复杂度稳定等于 O(n log n) 的归并排序要小很多。所以,对绝大多数顺序性较弱的随机数列而言,快速排序总是优于归并排序。它的主要缺点是非常脆弱,在实现时要非常小心才能避免低劣的性能。
# 第一种写法的平均空间复杂度为 O(nlogn)
def quickSort(nums):
if len(nums) <= 1:
return nums
pivot = nums[0] # 基准值
left = [nums[i] for i in range(1, len(nums)) if nums[i] < pivot]
right = [nums[i] for i in range(1, len(nums)) if nums[i] >= pivot]
return quickSort(left) + [pivot] + quickSort(right)
'''
@param nums: 待排序数组
@param left: 数组上界
@param right: 数组下界
'''
# 第二种写法的平均空间复杂度为 O(logn)
def quickSort2(nums, left, right):
# 分区操作
def partition(nums, left, right):
# 基准值
pivot = nums[left]
while left < right:
while left < right and nums[right] >= pivot:
right -= 1
# 比基准小的交换到前面
nums[left] = nums[right]
while left < right and nums[left] <= pivot:
left += 1
# 比基准大交换到后面
nums[right] = nums[left]
# 基准值的正确位置,也可以为 nums[right] = pivot
nums[left] = pivot
# 返回基准值的索引,也可以为 return right
return left
# 递归操作
if left < right:
pivotIndex = partition(nums, left, right)
# 左序列
quickSort2(nums, left, pivotIndex - 1)
# 右序列
quickSort2(nums, pivotIndex + 1, right)
return nums
希尔排序(Shell Sort)
希尔排序须知:
希尔排序是插入排序的一种更高效率的实现。它与插入排序的不同之处在于,它会优先比较距离较远的元素。
【例子】对于待排序列 {44,12,59,36,62,43,94,7,35,52,85},我们可设定增量序列为 {5,3,1}。
【解析】第一个增量为 5,因此 {44,43,85}、{12,94}、{59,7}、{36,35}、{62,52} 分别隶属于同一个子序列,子序列内部进行插入排序;然后选取第二个增量3,因此 {43,35,94,62}、{12,52,59,85}、{7,44,36} 分别隶属于同一个子序列;最后一个增量为 1,这一次排序相当于简单插入排序,但是经过前两次排序,序列已经基本有序,因此此次排序时间效率就提高了很多。
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法(第4版》的合著者 Robert Sedgewick 提出的。在这里,我就使用了这种方法。
def shellSort(nums):
lens = len(nums)
gap = 1
while gap < lens // 3:
# 动态定义间隔序列
gap = gap * 3 + 1
while gap > 0:
for i in range(gap, lens):
# curNum 保存当前待插入的数
curNum, preIndex = nums[i], i - gap
while preIndex >= 0 and curNum < nums[preIndex]:
# 将比 curNum 大的元素向后移动
nums[preIndex + gap] = nums[preIndex]
preIndex -= gap
# 待插入的数的正确位置
nums[preIndex + gap] = curNum
# 下一个动态间隔
gap //= 3
return nums
归并排序(Merge Sort)
归并排序须知:
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第2种方法)
自下而上的迭代
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。
def mergeSort(nums):
# 归并过程
def merge(left, right):
# 保存归并后的结果
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# 剩余的元素直接添加到末尾
result = result + left[i:] + right[j:]
return result
# 递归过程
if len(nums) <= 1:
return nums
mid = len(nums) // 2
left = mergeSort(nums[:mid])
right = mergeSort(nums[mid:])
return merge(left, right)
堆排序(Heap Sort)
堆排序须知:
堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
1.大根堆:每个节点的值都大于或等于其子节点的值,用于升序排列;
2.小根堆:每个节点的值都小于或等于其子节点的值,用于降序排列。
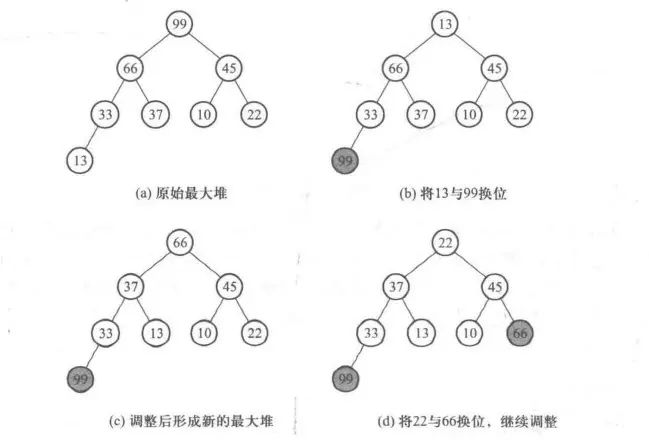
如下图所示,首先将一个无序的序列生成一个最大堆,如图(a)所示。接下来我们不需要将堆顶元素输出,只要将它与堆的最后一个元素对换位置即可,如图(b)所示。这时我们确知最后一个元素 99 一定是递增序列的最后一个元素,而且已经在正确的位置上。 现在问题变成了如何将剩余的元素重新生成一个最大堆——也很简单,只要依次自上而下进行过滤,使其符合最大堆的性质。图(c)是调整后形成的新的最大堆。要注意的是,99 已经被排除在最大堆之外,即在调整的时候,堆中元素的个数应该减 1 。结束第 1 轮调整后,再次将当前堆中的最后一个元素 22 与堆顶元素换位,如图(d)所示,再继续调整成新的最大堆……如此循环,直到堆中只剩 1 个元素,即可停止,得到一个从小到大排列的有序序列。
# 大根堆(从小打大排列)
def heapSort(nums):
# 调整堆
def adjustHeap(nums, i, size):
# 非叶子结点的左右两个孩子
lchild = 2 * i + 1
rchild = 2 * i + 2
# 在当前结点、左孩子、右孩子中找到最大元素的索引
largest = i
if lchild < size and nums[lchild] > nums[largest]:
largest = lchild
if rchild < size and nums[rchild] > nums[largest]:
largest = rchild
# 如果最大元素的索引不是当前结点,把大的结点交换到上面,继续调整堆
if largest != i:
nums[largest], nums[i] = nums[i], nums[largest]
# 第 2 个参数传入 largest 的索引是交换前大数字对应的索引
# 交换后该索引对应的是小数字,应该把该小数字向下调整
adjustHeap(nums, largest, size)
# 建立堆
def builtHeap(nums, size):
# 从倒数第一个非叶子结点开始建立大根堆
for i in range(len(nums)//2)[::-1]:
# 对所有非叶子结点进行堆的调整
adjustHeap(nums, i, size)
# 第一次建立好的大根堆
# print(nums)
# 堆排序
size = len(nums)
builtHeap(nums, size)
for i in range(len(nums))[::-1]:
# 每次根结点都是最大的数,最大数放到后面
nums[0], nums[i] = nums[i], nums[0]
# 交换完后还需要继续调整堆,只需调整根节点,此时数组的 size 不包括已经排序好的数
adjustHeap(nums, 0, i)
# 由于每次大的都会放到后面,因此最后的 nums 是从小到大排列
return nums
计数排序(Counting Sort)
计数排序须知:
计数排序要求输入数据的范围在 [0,N-1] 之间,则可以开辟一个大小为 N 的数组空间,将输入的数据值转化为键存储在该数组空间中,数组中的元素为该元素出现的个数。它是一种线性时间复杂度的排序。
def countingSort(nums):
# 桶的个数
bucket = [0] * (max(nums) + 1)
# 将元素值作为键值存储在桶中,记录其出现的次数
for num in nums:
bucket[num] += 1
# nums 的索引
i = 0
for j in range(len(bucket)):
while bucket[j] > 0:
nums[i] = j
bucket[j] -= 1
i += 1
return nums
桶排序(Bucket Sort)
桶排序须知:
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
为了使桶排序更加高效,我们需要做到这两点:
在额外空间充足的情况下,尽量增大桶的数量
使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
什么时候最快(Best Cases):
当输入的数据可以均匀的分配到每一个桶中
什么时候最慢(Worst Cases):
当输入的数据被分配到了同一个桶中
def bucketSort(nums, defaultBucketSize = 5):
maxVal, minVal = max(nums), min(nums)
# 如果没有指定桶的大小,则默认为5
bucketSize = defaultBucketSize
# 数据分为 bucketCount 组
bucketCount = (maxVal - minVal) // bucketSize + 1
# 二维桶
buckets = []
for i in range(bucketCount):
buckets.append([])
# 利用函数映射将各个数据放入对应的桶中
for num in nums:
buckets[(num - minVal) // bucketSize].append(num)
# 清空 nums
nums.clear()
# 对每一个二维桶中的元素进行排序
for bucket in buckets:
# 假设使用插入排序
insertionSort(bucket)
# 将排序好的桶依次放入到 nums 中
nums.extend(bucket)
return nums
基数排序(Radix Sort)
基数排序须知:
基数排序是桶排序的一种推广,它所考虑的待排记录包含不止一个关键字。例如对一副牌的整理,可将每张牌看作一个记录,包含两个关键字:花色、面值。一般我们可以将一个有序列是先按花色划分为四大块,每一块中又再按面值大小排序。这时“花色”就是一张牌的“最主位关键字”,而“面值”是“最次位关键字”。
基数排序有两种方法:
1.MSD (主位优先法):从高位开始进行排序
2.LSD (次位优先法):从低位开始进行排序
# LSD Radix Sort
def radixSort(nums):
mod = 10
div = 1
# 最大数的位数决定了外循环多少次
mostBit = len(str(max(nums)))
# 构造 mod 个空桶
buckets = [[] for row in range(mod)]
while mostBit:
# 将数据放入对应的桶中
for num in nums:
buckets[num // div % mod].append(num)
# nums 的索引
i = 0
# 将数据收集起来
for bucket in buckets:
while bucket:
# 依次取出
nums[i] = bucket.pop(0)
i += 1
div *= 10
mostBit -= 1
return nums