离散蚁群算法实例(求解旅行商问题)
蚁群算法
蚁群算法原理
万字长文带你了解蚁群算法及求解复杂约束问题【源码实现】
上面这篇博文的蚁群算法是实数编码。今天讲解下离散编码的蚁群算法。
算法原理不再解释,直接上算例。
旅行商问题
旅行商问题(TSP 问题)。假设有一个旅行商人要拜访全国31个省会城市,他需要选择所要走的路径,路径的限制是每个城市只能拜访-一次, 而且最后要回到原来出发的城市。路径的选择要求是:所选路径的路程为所有路径之中的最小值。
matlab求解
%%%%%%%%%%%%%%%%%%%%蚁群算法解决TSP问题%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
citys=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
3238 1229;4196 1044;4312 790;4386 570;3007 1970;2562 1756;...
2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;...
3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
2370 2975]; %31个省会城市坐标
%%%%%%%%%%%%%%%%%%%%%%%计算城市间相互距离%%%%%%%%%%%%%%%%%%%%%%%
%% 计算距离
n = size(citys,1);%n=31
D = zeros(n,n);%因为是计算两两之间的距离,所以矩阵为31*31
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4; %对角矩阵 距离为0,我将对角矩阵赋值一个很小的距离,不影响计算。因为前文图中公式里有距离的倒数
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%初始化参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 初始化参数
m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 200; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
%%%%%%%%%%%%%%%%%%%%%%%%%迭代%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 迭代寻找最佳路径
while iter <= iter_max
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m %遍历每一个蚂蚁
temp = randperm(n);%randperm(n)产生1-n的随机序列
start(i) = temp(1); %起始点赋值
end
Table(:,1) = start; %% Table路径记录表
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);%取出未访问过的城市索引
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
iter = iter + 1;
Table = zeros(m,n);
end
%% VI. 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
%% VII. 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
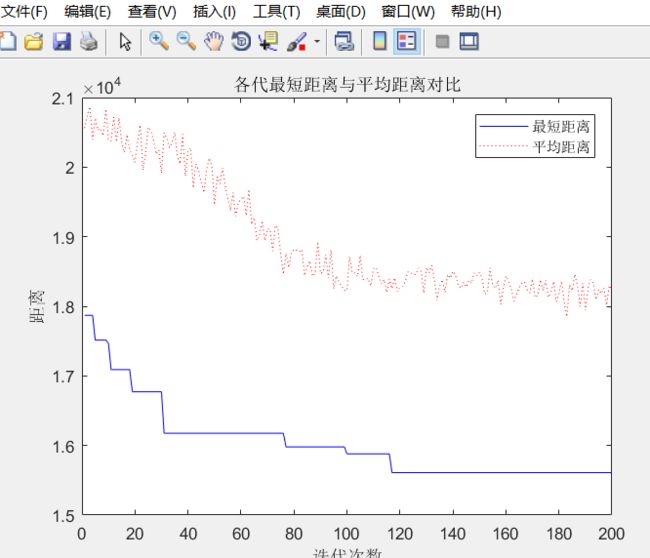
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')

python求解
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: yudengwu(余登武)
# @Date : 2021/5/28
#@email:[email protected]
import numpy as np
from tqdm import tqdm#进度条设置
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib; matplotlib.use('TkAgg')
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
import math
#====================距离文件=================
C=[1304 ,2312,3639 ,1315,4177 ,2244,3712 ,1399,3488, 1535,3326, 1556,
3238 ,1229,4196 ,1044,4312,790,4386,570,3007,1970,2562 ,1756,
2788, 1491,2381 ,1676,1332,695,3715 ,1678,3918,2179,4061,2370,
3780, 2212,3676, 2578,4029,2838,4263,2931,3429,1908,3507,2376,
3394 ,2643,3439,3201,2935,3240,3140,3550,2545,2357,2778,2826,
2370 ,2975] #31个省会城市坐标
C=np.array(C).reshape(-1,2)#shape=(31, 2)
#===============蚁群算法 TSP求解====================
class ACA_TSP(object):
def __init__(self,C):
self.C = C # 城市坐标
self.AntCount = 100 #蚂蚁数量
self.city_count = self.C.shape[0] # 城市数量
self.alpha = 1 # 信息素重要程度因子
self.beta = 2 # 启发函数重要程度因子
self.rho = 0.1 # 挥发速度
self.MAX_iter = 100 # 最大迭代次数
self.Distance=self.calculate_distance(self.C[:,0], self.C[:,1])#任意两个城市距离间隔矩阵 shape=(31, 31)
self.Q = 1
# 初始信息素矩阵,全是为1组成的矩阵
self.pheromonetable = np.ones((self.city_count, self.city_count))
# 候选集列表,存放100只蚂蚁的路径(一只蚂蚁一个路径),一共就Antcount个路径,一共是蚂蚁数量*31个城市数量
self.candidate = np.zeros((self.AntCount, self.city_count)).astype(int)
# path_best存放的是相应的,每次迭代后的最优路径,每次迭代只有一个值
self.path_best = np.zeros((self.MAX_iter, self.city_count))
# 存放每次迭代的最优距离
self.distance_best = np.zeros(self.MAX_iter)
#城市间的距离
def calculate_distance(self,X, Y):
"""
建立一个citycount-citycount二维数组,存放每对城市之间的距离.
注意,因为要根据距离矩阵求启发函数 η \eta ηij( η \eta ηij为城市i和城市j之间距离的倒数),
所有距离矩阵的对角线不能为0,我把对角线设置为inf,其实只要不为零就可以。
计算城市两辆之间的欧式距离,结果用numpy矩阵存储
:param X: 城市的X坐标,np.array数组
:param Y: 城市的Y坐标,np.array数组
"""
distance_matrix = np.zeros((self.city_count, self.city_count))
for i in range(self.city_count):
for j in range(self.city_count):
if i == j:
distance_matrix[i][j] = np.inf
else:
dis = np.sqrt((X[i] - X[j]) ** 2 + (Y[i] - Y[j]) ** 2) # 欧式距离计算
distance_matrix[i][j] = dis
return distance_matrix
def main(self):
# 倒数矩阵
etable = 1.0 / self.Distance
for iter in tqdm(range(self.MAX_iter)):#遍历每一次迭代
# first:蚂蚁初始点选择
if self.AntCount <= self.city_count:
# np.random.permutation随机排列一个数组的
self.candidate[:, 0] = np.random.permutation(range(self.city_count))[:self.AntCount]
else:
m = self.AntCount - self.city_count
n = 2
self.candidate[:self.city_count, 0] = np.random.permutation(range(self.city_count))[:]
while m > self.city_count:
self.candidate[self.city_count * (n - 1):self.city_count * n, 0] = np.random.permutation(range(self.city_count))[:]
m = m - self.city_count
n = n + 1
self.candidate[self.city_count * (n - 1):self.AntCount, 0] = np.random.permutation(range(self.city_count))[:m]
length = np.zeros(self.AntCount) # 每次迭代的N个蚂蚁的距离值
# second:选择下一个城市选择
for i in range(self.AntCount):#遍历每一次蚂蚁
# 移除已经访问的第一个元素
unvisit = list(range(self.city_count)) # 列表形式存储没有访问的城市编号
visit = self.candidate[i, 0] # 当前所在点,第i个蚂蚁在第一个城市
unvisit.remove(visit) # 在未访问的城市中移除当前开始的点
for j in range(1, self.city_count): # 访问剩下的city_count个城市,city_count次访问
protrans = np.zeros(len(unvisit)) # 每次循环都更改当前没有访问的城市的转移概率矩阵1*30,1*29,1*28...
# 下一城市的概率函数
for k in range(len(unvisit)):
# 计算当前城市到剩余城市的(信息素浓度^alpha)*(城市适应度的倒数)^beta
# etable[visit][unvisit[k]],(alpha+1)是倒数分之一,pheromonetable[visit][unvisit[k]]是从本城市到k城市的信息素
protrans[k] = np.power(self.pheromonetable[visit][unvisit[k]], self.alpha) * np.power(
etable[visit][unvisit[k]], (self.alpha + 1))
# 累计概率,轮盘赌选择
cumsumprobtrans = (protrans / sum(protrans)).cumsum()
cumsumprobtrans -= np.random.rand()
# 求出离随机数产生最近的索引值
k = unvisit[list(cumsumprobtrans > 0).index(True)]
# 下一个访问城市的索引值
self.candidate[i, j] = k
unvisit.remove(k)
length[i] += self.Distance[visit][k]
visit = k # 更改出发点,继续选择下一个到达点
length[i] += self.Distance[visit][self.candidate[i, 0]] # 最后一个城市和第一个城市的距离值也要加进去
"""
更新路径等参数
"""
# 如果迭代次数为一次,那么无条件让初始值代替path_best,distance_best.
if iter == 0:
self.distance_best[iter] = length.min()
self.path_best[iter] = self.candidate[length.argmin()].copy()
else:
# 如果当前的解没有之前的解好,那么当前最优还是为之前的那个值;并且用前一个路径替换为当前的最优路径
if length.min() > self.distance_best[iter - 1]:
self.distance_best[iter] = self.distance_best[iter - 1]
self.path_best[iter] = self.path_best[iter - 1].copy()
else: # 当前解比之前的要好,替换当前解和路径
self.distance_best[iter] = length.min()
self.path_best[iter] = self.candidate[length.argmin()].copy()
"""
信息素的更新
"""
# 信息素的增加量矩阵
changepheromonetable = np.zeros((self.city_count, self.city_count))
for i in range(self.AntCount):
for j in range(self.city_count - 1):
# 当前路径比如城市23之间的信息素的增量:1/当前蚂蚁行走的总距离的信息素
changepheromonetable[self.candidate[i, j]][self.candidate[i][j + 1]] += self.Q / length[i]
# Distance[candidate[i, j]][candidate[i, j + 1]]
# 最后一个城市和第一个城市的信息素增加量
changepheromonetable[self.candidate[i, j + 1]][self.candidate[i, 0]] += self.Q / length[i]
# 信息素更新的公式:
pheromonetable = (1 - self.rho) * self.pheromonetable + changepheromonetable
print("蚁群算法的最优路径", self.path_best[-1] + 1)
print("迭代", self.MAX_iter, "次后", "蚁群算法求得最优解", self.distance_best[-1])
aca_tsp=ACA_TSP(C)
aca_tsp.main()

算出来的不是最优解,目前我对离散蚁群算法理解还不是很深,所以写出来的代码可能不是很好。先这样吧。
![]()
