算法：递归与分治策略

分治策略与递归

---

---

一、分治策略与递归概念

分治策略：是将规模比较大的问题可分割成规模较小的相同问题。问题不变，规模变小。这自然导致送归过程的产生。分治与递归像一对李生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

递归：若一个函数直接地或间接地调用自己则称这个函数是递归的函数。（简单地描述为＂自己调用自己”)。

分治法所能解决的问题一股具有以下四个特征：
●该问题的规模缩小到一定的程度就可以容易地解决。
●该问题可以分解为若干个规模较小的相同问题。
●使用小规模的解可以合并成，该问题原规模的解。
●该问题所分解出的各个子规模是相互独立的。

分治法步骤：在分治策略中递归地求解一个问题，在每层递归中应用如下三个步骤：

1. 分解：将问题划分成一些子问题，子题的形式与原问题一样，只是规模更小。
2. 解缺：递归地求解子问题。如果子问题的规模足够小，则停止递归，直接求解。
3. 合并：将小规模的解组合成原规模问题的解。

二、求解n的阶乘。（不考虑int溢出）

//循环求解n的阶乘     // O(n) // S(1)
int fun(int n) 
{
	int sum = 1;
	for (int i = 1;i<=n ; ++i)
	{
		sum = sum * i;
	}
	return sum;
}

//递归求解n的阶乘  //O(n) , S(n)
int fac(int n)
{
	if (n <= 1) 
		return 1;
	else
		return fac(n - 1) * n;
}
 
int main()
{
	int sum = fac(4);

	return 0;
}

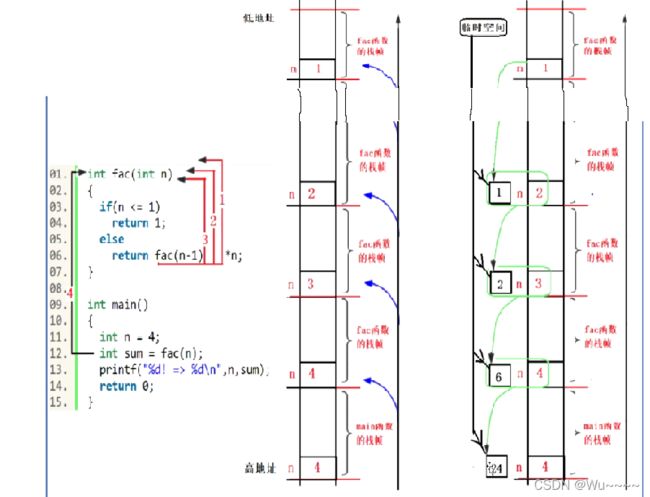
递归函数的执行分为“递推”和＂回归" 两个过程，两个过程由递归终止条件控制，即逐层递推，直至递归终止条件满足，终止递归，然后逐层回归。
递归调用同普通的函数调用一样，每当调用发生时，就要分配新的钱帧（形参数据，现场保护，局部变量）；而与普通的函数调用不同的是，于递推的过程是一个逐层调用的过程，因此存在一个逐层连续的分配栈过程，直至到
递归终止条件时，才开始回归，这时才逐层释放栈帧空间，返回到上一层，直最后返回到主调函数。

递归调用：

三、打印函数

//循环完成打印函数
void Print_Ar(const int* br, int n)
{
	if (br == NULL) return;
	for (int i = 0; i < n; ++i)
	{
		cout<<br[i]<<endl;
	}
	cout<<endl;
}

//递归实现
void Print(const int* br, int &n)
{
	if (n > 0)
	{
		Print(br, n-1);
		cout << br[n-1] << " ";
	}
}
void Print_Ar(const int* br, int n)
{
	if (br == NULL || n < 1) return;
	Print(br, n);
	cout << endl;
}
int main()
{
	int ar[] = { 12,23,34 };
	int n = sizeof(ar) / sizeof(ar[0]);
	Print_Ar(ar, n);
	return 0;
}

void Print(const int* br, int &n)
{
if (n > 0)
{
cout << br[n-1] << " ";
Print(br, n-1);
}
}
打印结果为34，23，12.

void Print(const int* br, int &n)
{
if (n > 0)
{
Print(br, --n);
cout << br[n] << " ";
}
}
递归调用时，整型数值n最好不要用前置渐渐或后置减减。
n-- 可能会栈溢出； —n可能会越界。

四、查找函数

//循环完成查找函数,返回下标
int FindPos(const int* br, int n, int val)
{
	if (br == NULL || n < 1) return -1;
	int pos = n - 1;
	while (pos >= 0 && br[pos] != val)
	{
		--pos;
	}
	return pos;	
}

//递归完成
int Find(const int* br, int n, int val)
{
	if (n <= 0 || br[n - 1] == val)
	{
		return n -1;
	}
	else
	{
		return Find(br, n - 1, val);
	}
}
int FindPos(const int* br, int n, int val)
{
	if (br == NULL || n < 1) return -1;
	return Find(br, n, val);
}
int main()
{
	int ar[] = { 12,56,34,78 };
	int n = sizeof(ar) / sizeof(ar[0]);
	int val = 78;  // 12 ;/// 34  // 100
	int pos = FindPos(ar, n, val);

	cout << pos << endl;

}