第6章在泛泛而谈,初学者感觉很难了解到实际性的东西,不过也根据章节结构结合相关资料做下梳理。
6.1 XOR
**
6.2 基于梯度的学习
参考链接:An overview of gradient descent optimization algorithms
梯度下降法:
拟合函数:
损失函数
梯度:
迭代过程:沿着负梯度方向更新参数,其中为学习率(learning rate)或称步长,直到达到终止条件。
(1)三种梯度下降变体
a.全量梯度下降法(Batch gradient descent)
采用全部训练样本更新参数
for i in range ( nb_epochs ): # nb_epochs 为最大迭代次数
params_grad = evaluate_gradient ( loss_function , data , params )
params = params - learning_rate * params_grad
使用全部训练集,可以保证每次更新都会朝着正确的方向进行,最后收敛于极值点;但是学习时间太长,计算冗余且不能进行在线模型参数更新。
b.随机梯度下降法(Stochastic gradient descent)
每次从训练样本中随机取一个样本来更新参数
for i in range ( nb_epochs ):
np.random.shuffle( data )
for example in data :
params_grad = evaluate_gradient ( loss_function , example , params )
params = params - learning_rate * params_grad
计算速度快,但每次更新不一定会按照正确的方向进行,造成扰动,使得迭代次数增多,即收敛速度变慢,最终会收敛于极值点。
c.批量梯度下降(Mini-batch gradient descent)
每次从所有的训练样本中选取一部分样本来更新模型参数。
for i in range ( nb_epochs ):
np.random.shuffle( data )
for batch in get_batches ( data , batch_size =50):
params_grad = evaluate_gradient ( loss_function , batch , params )
params = params - learning_rate * params_grad
相对于SGD,更新过程更加稳定;相对于全量梯度下降,学习速度加快。
(2)挑战
-
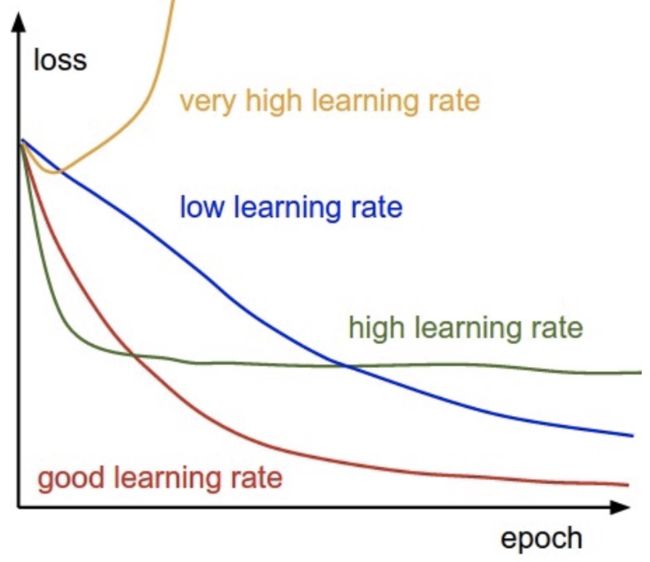
选择合适的learning rate.lr过小,收敛速度太慢;lr过大,会出现在极值点附近震荡
learnig rate schedules。目的是每次在更新参数时改变其学习速率。pytorch的learning rate schedule:LambdaLR,StepLR,MultiStepLR,ExponentialLR,CosineAnnealingLR,ReduceLROnPlateau
模型的参数更新都是使用相同的学习速率。如果数据特征相对稀疏或者每个特征有着不同的分布,我们并不希望对所有参数适用相同的学习速率,对某些几乎很少出现的特征用较大的学习速率。
对于非凸目标函数,容易陷入局部极小值。在神经网络的过程中,要尽量避免这个问题。但Dauphin在《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》指出更严重的是鞍点(saddle point)(鞍点处的梯度为零,鞍点通常被相同误差值的平面所包围(这个平面又叫Plateaus,Plateaus是梯度接近于零的平缓区域,会降低神经网络学习速度)。高位特征空间中这个鞍点附近的平坦区域范围可能非常大,这使得SGD算法很难脱离区域,即可能会长时间卡在该点附近(因为梯度在所有维度上接近于零))
(3)梯度下降优化算法(Gradient descent optimization algorithms)
a.Momentum
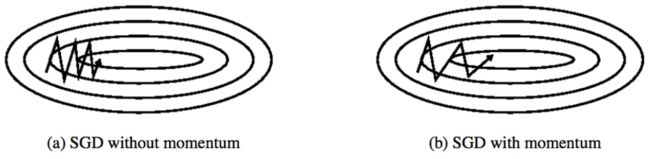
冲量梯度下降法就是在原来的梯度上加上了冲量(积累量)。个人理解就是当梯度与冲量方向一致时,增加参数更新的增量,加快了收敛;当梯度与冲量方向不一致时,减少了增量,使得参数更新过程的震荡减少。本质上与SGD没有区别。
b.Nesterov accelerated gradient
NAG比Momentum的速度更快,因为把原来计算换成计算,就是在提前计算了下一个梯度。
c.Adagrad
前面的两种方法,在更新参数时,学习速率并没有发生变化。Adagrad是一种自适应学习速率的梯度优化算法。对于更新频繁的参数,学习速率会较小,对于更新不频繁的参数,学习速率会较大,挺适合处理适合处理稀疏特征数据。
是个对角矩阵,其中第i行的对角元素为过去到当前第i个参数的梯度的平方和,为平滑参数,避免分母为0,通常取1e-8。开根号只是为了优化下算法性能。
从公式可以看出,的对角元素的值是不断累加的,学习速率衰减很快。为了避免学习速率衰减过快的问题,提出Adadelta算法
d.Adadelta
学习率衰减的分母采用梯度平方的移动平均。
得到
上式有个问题在于和的单位不匹配,故采用参数更新的平方的移动平均来替代学习率。
得到
(当前未知)
e.RMSprop
RMSprop其实就是Adadelta的中间形式,即
f.Adam
Adam算法式结合了RMSprop和Momentum,即
在进行偏差修正。(可以了解下指数加权平均的偏差修正(Bias correction in exponentially weighted averages)),得到:
最终得到参数的更新公式为:
g.AdaMax
中的就相当于对的范数,将其泛化到范数。虽然当p值较大时,数值会变得不稳定。但当p—>时,得到:
=
用替代Adam中的得到
h.Nadam
借鉴Adam和NAG算法
先看下NAG算法,在提前计算下一个梯度,即
Nadam中把这种“先见之明”的思想用到了对参数的更新上,可以看下这个过程:
,
先记下这个“先见之明”,之后会用到
回顾Adam的公式
,拆分得到,
=
应用下“先见之明”,Nadam对参数的更新为
来一张现成的图对比下上文提到的几个梯度:
来源:http://cs231n.github.io/neural-networks-3/,原地址是动图
从左图中可以看到,SGD很慢,但会往正确的方向前进,Momentum和NAG速度较快,但有很大的偏离,NAG由于提前预估下一梯度的位置,因此对偏离的响应会快一点。而 Adagrad、Adadelta与RMSprop由于具有自适应学习率的能力,能够快速在正确的方向上得到收敛。
从右图可以看出,SGD基本就在鞍点附近震荡,很难脱离鞍点。而Momentum和NAG本质没有自适应学习率,一开始仍然在鞍点附近震荡,但由于速度会比SGD快,荡久了然后脱离了鞍点。其他三种Adagrad、Adadelta与RMSprop很快脱离了鞍点。