不同领域的人在看完同一部电影后,会有不同的感想(如果你检索《流浪地球》这一关键词的话,你会看到大家社会学,心理学,物理学等等各个角度的多维解析,真的开心自己处在这个多元开放的时代中✧٩(ˊωˋ*)و✧),这里想分享一下我看完《流浪地球》后的感想。(电影不是白看的(っ╥╯﹏╰╥c)要写些东西纪念一下)
于是下面就是感想:集体主义最终胜利真的太好啦,超喜欢大刘的想象力和小说深度,电影特效也超好的,这个春节真的开心^_^
然而让我只考虑这些文学社会学的事情是很难为人的╮( •́ω•̀ )╭
所以我同时受到了科幻电影的积极影响:探索了一下其中的 Roche limit (洛希极限)。如果你还没有害怕接下来要发生的事,我很乐意继续分享自己的成果੭ ᐕ)੭*⁾⁾
Sure, Roche limit (in celestial mechanics) is a distance between two bodies, probably, stars, within which the small body will disintegrated by the gravity produced by the large mass one. The "limit" also means that a body cannot continue to absorb any materials when the radius reach the Roche limit, it will lose its mass when reaches.
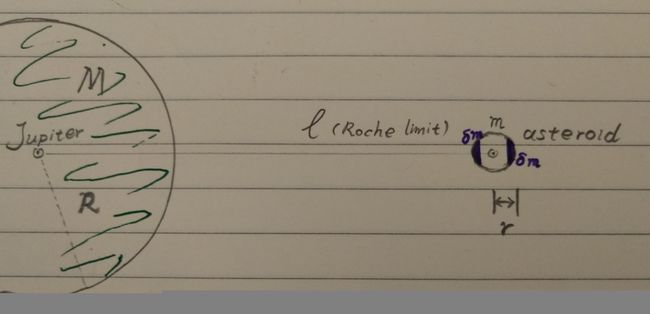
As the pictures below told, when the tininess one arrive at this "death distance" there will exists the difference of grivity named tidal force, which can make the asteroid disintegrate from both ends (the nearest end N and the farthest end F).
When it evolves like this, N will likely to get a higher revolution speed, and F will get a smaller one, which will lead to further disintegration, and the debris left behind will be distributed around the circumference of the Roche radius.
It is known to all that the gravity of a sphere can be shown by the equation named "Law of universal gravitation" (Issac Newton proved)
,
I'll show you Roche limit of the situation when the two bodies are all stars(solid), with uniform mass distribution and are all ideal sphere. The figure next will give you some parameters already known.
Hence, the centrifugal force from the rotation is
(that is, the asteroid is "obiting in a nearly-circular orbit with synchronous rotation")
,
Each small ends of the asteroid is attracted by the large mass with Law of universal gravitation, hence they will face the difference ,named the tidal force , we can use the defination to calculate it
,
from which we can make further operation, make approximation , we have
,
make the force balance with the grivity and tidal force
,
finally to have the Roche limit is
,
if use and ,
,
That is the accurate formula of Roche limit, when the rotation isn't exist, replace "3" with "2".
由上述分析我们就能粗略地解决这样一个问题:地球作为 asteroid 的话,木星的 Roche limit 为多少?
我们可以知道地球的半径为6,378,137m,密度为5513kg/m^3,木星半径为71,493,000m,密度为1,326kg/m^3,从而可以得到。
这就是地球即将瓦解的距离,即 Roche limit .
在人类天文学观测的历史中,的确曾经出现过彗星进入 Roche limit 而被木星(Jupiter)潮汐力撕碎的事件,此事件发生于1992年,这形成了木星的行星环(由于瓦解后的每个碎片都不止是由万有引力来维持其形态,故能够存在与 Roche limit 内部)。