【数字信号处理】线性时不变系统 LTI ( 判断某个系统是否是 “ 非时变 “ 系统 | 案例二 )
文章目录
- 一、判断系统是否 " 非时变 "
-
- 1、案例二
-
- ① 时不变系统概念
- ② 先变换后移位
- ③ 先移位后变换
- ④ 结论
一、判断系统是否 " 非时变 "
1、案例二
给定 输入序列 x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 , 0 } x(n) = \{ 0, 1 , 2, 3, 4, 5 , 0 \} x(n)={0,1,2,3,4,5,0} , n n n 取值 − 1 -1 −1 ~ 5 5 5
判断其输出序列 y ( n ) = x ( 2 n ) y(n) = x(2n) y(n)=x(2n) 的 " 变换 " 操作是否是 " 时不变 " 的 ;
y ( n ) y(n) y(n) 只有在 n = 0 , 1 , 2 n = 0 , 1 , 2 n=0,1,2 取值时 , 才有值 ,
如果 n = − 1 n = -1 n=−1 , 2 n = − 2 2n = -2 2n=−2 , x ( − 2 ) x(-2) x(−2) 没有值 ;
如果 n = 3 n = 3 n=3 , 2 n = 6 2n = 6 2n=6 , x ( 6 ) x(6) x(6) 没有值 ;
如果 n = 4 n = 4 n=4 , 2 n = 8 2n = 8 2n=8 , x ( 8 ) x(8) x(8) 没有值 ;
如果 n = 5 n = 5 n=5 , 2 n = 10 2n = 10 2n=10 , x ( 10 ) x(10) x(10) 没有值 ;
因此 , 正常变换后 , y ( n ) y(n) y(n) 的取值是 n = 0 , 1 , 2 n = 0 , 1 , 2 n=0,1,2 时的取值 ,
当 n = 0 n = 0 n=0 时 , y ( n ) = x ( 2 n ) = x ( 0 ) = 1 y(n) = x(2n) = x(0) = 1 y(n)=x(2n)=x(0)=1 ;
当 n = 1 n = 1 n=1 时 , y ( n ) = x ( 2 n ) = x ( 2 ) = 3 y(n) = x(2n) = x(2) = 3 y(n)=x(2n)=x(2)=3 ;
当 n = 2 n = 2 n=2 时 , y ( n ) = x ( 2 n ) = x ( 4 ) = 5 y(n) = x(2n) = x(4) = 5 y(n)=x(2n)=x(4)=5 ;
x ( n ) x(n) x(n) 正常变换后的取值为 :
y ( n ) = { 1 , 3 , 5 } y(n) = \{ 1, 3, 5 \} y(n)={1,3,5}
① 时不变系统概念
时不变系统 ( time-invariant ) : 系统特性 , 不随着时间的变化而变化 ;
y ( n − m ) = T [ x ( n − m ) ] y(n - m) = T[x(n-m)] y(n−m)=T[x(n−m)]
输入延迟后 , 输出也随之延迟 ;
与 " 时不变 " 系统对应的是 " 时变 " 系统 ;
② 先变换后移位
将 " 输出序列 " 进行移位 , 先 " 变换 " 后 " 移位 " ;
先将 " 输入序列 " 进行 " 变换 " 操作 , 得到 " 输出序列 " , 然后对 输出序列 进行 " 移位 " 操作 ;
其中 " 变换 " 指的是 , 离散时间系统 , 将 " 输入序列 " 变换 为 " 输出序列 " , 输入序列 到 输出序列 之间的操作 , 是 " 变换 " ;
变换操作 : 先将 输入序列 x ( n ) x(n) x(n) 进行 变换 操作 , 得到 输出序列 x ( 2 n ) x(2n) x(2n) ,
移位操作 : 然后 对 x ( 2 n ) x(2n) x(2n) 输出序列 进行移位 n − n 0 n - n_0 n−n0 得到 x ( 2 ( n − n 0 ) ) x(2(n-n_0)) x(2(n−n0)) ,
完整运算过程如下 :
y ( n − n 0 ) = x ( 2 ( n − n 0 ) ) y(n - n_0) = x(2(n-n_0)) y(n−n0)=x(2(n−n0))
先变换 , 变换后输出为 :
y ( n ) = { 1 , 3 , 5 } y(n) = \{ 1, 3, 5 \} y(n)={1,3,5}
后移位的取值为 : 向右移一位 ;
y ( n − 1 ) = { 0 , 1 , 3 , 5 } y(n-1) = \{ 0, 1, 3, 5 \} y(n−1)={0,1,3,5}
③ 先移位后变换
将 " 输入序列 " 进行移位 , 先进行移位 , 将 " 输入序列 x ( n ) x(n) x(n) " 先进行 " 移位 " 操作 , 得到 新的 " 输入序列 " 为 x ( n − n 0 ) x(n-n_0) x(n−n0) , 然后 对新的输入序列进行 " 变换 " 操作 , 得到 " 输出序列 " ;
变换过程是 T [ x ( n − n 0 ) ] = x ( 2 n − n 0 ) T[x(n - n_0)] = x(2n - n_0) T[x(n−n0)]=x(2n−n0) , 变换时 , 只是将 n n n 值变为 2 n 2n 2n , n 0 n_0 n0 值不动 ;
x ( n − n 0 ) x(n-n_0) x(n−n0) 变换时 , 只将 n n n 乘以 2 2 2 , n 0 n_0 n0 不变 , 变换结果如为 x ( 2 n − n 0 ) x(2n - n_0) x(2n−n0) ;
完整过程如下 :
T [ x ( n − n 0 ) ] = x ( 2 n − n 0 ) T[x(n - n_0)] = x(2n - n_0) T[x(n−n0)]=x(2n−n0)
先将 x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 , 0 } x(n) = \{ 0, 1 , 2, 3, 4, 5 , 0 \} x(n)={0,1,2,3,4,5,0} , n n n 取值 − 1 -1 −1 ~ 5 5 5 , 向右移位 , 移位后的序列 :
x ( n ) = { 0 , 1 , 2 , 3 , 4 , 5 } x(n) = \{ 0, 1 , 2, 3, 4, 5 \} x(n)={0,1,2,3,4,5} n n n 取值 0 0 0 ~ 6 6 6 , 移位后的序列图式如下 :
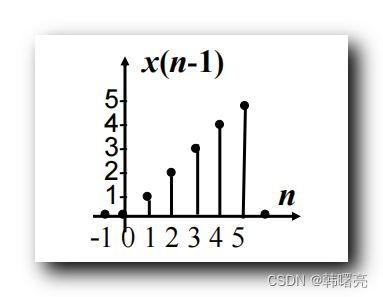
向右移位 1 后 , n n n 取值 由原来的 − 1 -1 −1 ~ 5 5 5 变为了 0 0 0 ~ 6 6 6 ,
y ( n ) y(n) y(n) 只有在 n = 0 , 1 , 2 , 3 n = 0 , 1 , 2 , 3 n=0,1,2,3 取值时 , 才有值 ,
如果 n = 4 n = 4 n=4 , 2 n = 8 2n = 8 2n=8 , x ( 8 ) x(8) x(8) 没有值 ;
如果 n = 5 n = 5 n=5 , 2 n = 10 2n = 10 2n=10 , x ( 10 ) x(10) x(10) 没有值 ;
因此 , 正常变换后 , y ( n ) y(n) y(n) 的取值是 n = 0 , 1 , 2 n = 0 , 1 , 2 n=0,1,2 时的取值 ,
当 n = 0 n = 0 n=0 时 , y ( n ) = x ( 2 n ) = x ( 0 ) = 0 y(n) = x(2n) = x(0) = 0 y(n)=x(2n)=x(0)=0 ;
当 n = 1 n = 1 n=1 时 , y ( n ) = x ( 2 n ) = x ( 2 ) = 2 y(n) = x(2n) = x(2) = 2 y(n)=x(2n)=x(2)=2 ;
当 n = 2 n = 2 n=2 时 , y ( n ) = x ( 2 n ) = x ( 4 ) = 4 y(n) = x(2n) = x(4) = 4 y(n)=x(2n)=x(4)=4 ;
当 n = 3 n = 3 n=3 时 , y ( n ) = x ( 2 n ) = x ( 6 ) = 0 y(n) = x(2n) = x(6) = 0 y(n)=x(2n)=x(6)=0 ;
x ( n − 1 ) x(n - 1) x(n−1) 正常变换后的取值为 :
T ( x ( n − 1 ) ) = { 0 , 2 , 4 , 0 } T(x(n -1 )) = \{ 0, 2, 4, 0 \} T(x(n−1))={0,2,4,0}
④ 结论
先 " 变换 " 后 " 移位 " , 结果是 x ( 2 ( n − n 0 ) ) x(2(n-n_0)) x(2(n−n0)) , 输出序列 为 y ( n − 1 ) = { 0 , 1 , 3 , 5 } y(n-1) = \{ 0, 1, 3, 5 \} y(n−1)={0,1,3,5}
先 " 移位 " 后 " 变换 " , 结果是 x ( 2 n − n 0 ) x(2n - n_0) x(2n−n0) , 输出序列为 T ( x ( n − 1 ) ) = { 0 , 2 , 4 , 0 } T(x(n -1 )) = \{ 0, 2, 4, 0 \} T(x(n−1))={0,2,4,0}
该系统是 " 时变系统 " ;
