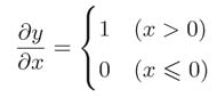《深度学习入门：基于Python的理论与实现》读书笔记：第5章 误差反向传播算法

目录

第5章 误差反向传播算法

5.1 计算图

5.1.1 用计算图求解

5.1.2 局部计算

5.1.3 为何用计算图解题

5.2 链式法则

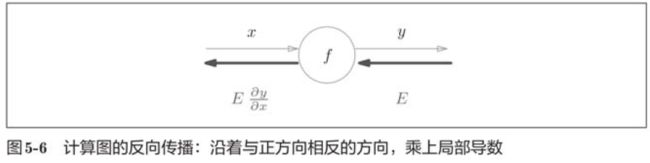
5.2.1 计算图的反向传播

5.2.2 什么是链式法则

5.2.3 链式法则和计算图

5.3 反向传播

5.3.1 加法节点的反向传播 

5.3.2 乘法节点的反向传播

5.3.3 苹果的例子

5.4 简单层的实现

5.4.1 乘法层的实现

5.4.2 加法层的实现

5.5 激活函数层的实现

5.5.1 ReLu层

5.5.2 Sigmoid层

 5.6 Affine/Softmax层的实现

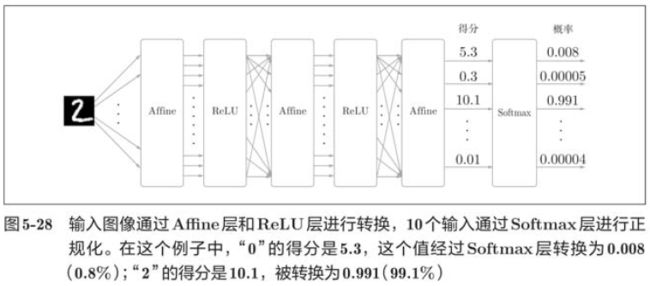
5.6.1 Affine层

5.6.2 批版本的Affine层

5.6.3 Softmax-with-Loss层 

5.7 误差反向传播法的实现

5.7.1 神经网络学习的全貌图

5.7.2 对应误差反向传播法的神经网络的实现 

5.7.3 误差反向传播法的梯度确认

5.7.4 使用误差反向传播法的学习

5.8 小结

 

---

第5章 误差反向传播算法

5.1 计算图

计算图将计算过程用图形表示出来，这里说的图形是数据结构图，通过多个节点和边表示（连接节点的直线称为“边”）。

5.1.1 用计算图求解

用计算图解题的情况下，需要按如下流程进行：

1.构建计算图；

2.在计算图上，从左向右进行计算。

这里的第2步“从左向右进行计算”是一种正方向上的传播，简称为正向传播，正向传播是从计算图出发点到结束点的传播。既然有正向传播这个名称，当然也可以考虑反向的传播。实际上，这种传播称为反向传播，反向传播将在接下来的导数计算中发挥重要作用。

5.1.2 局部计算

计算图的特征是可以通过传递“局部计算”获得最终结果。“局部”这个词的意思是“与自己相关的某个小范围”。局部计算是指，无论全局发生了什么，都能只根据与自己相关的信息输出接下来的结果。

计算图可以集中精力于局部计算，无论全局的计算有多么复杂，各个步骤所要做的就是对象节点的局部计算。虽然局部计算非常简单，但是通过传递它的计算结果，可以获得全局的复杂计算的结果。

5.1.3 为何用计算图解题

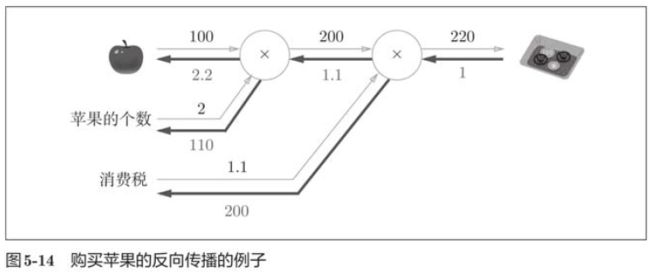
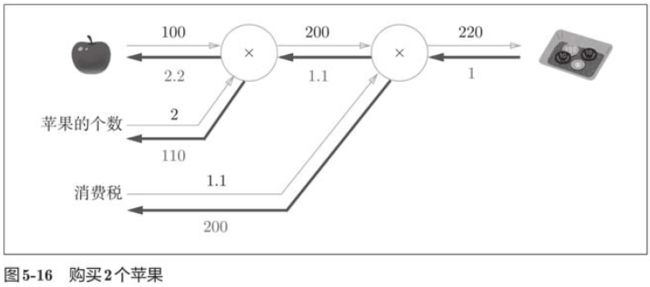
如图所示，反向传播使用与正方向相反的箭头（粗线）表示，传递“局部导数” ，将导数的值写在箭头的下方。

这里只求了关于苹果的价格的导数，不过“支付金额关于消费税的导数”“支付金额关于苹果的个数的导数”等也都可以用同样的方式算出来。并且，计算中途求得的导出的结果（中间传递的导数）可以被共享，从而可以高效地计算多个导数。综上，计算图的优点是，可以通过正向传播和反向传播高效地计算各个变量的导数值。

5.2 链式法则

5.2.1 计算图的反向传播

5.2.2 什么是链式法则

如果某个函数由复合函数表示，则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。

5.2.3 链式法则和计算图

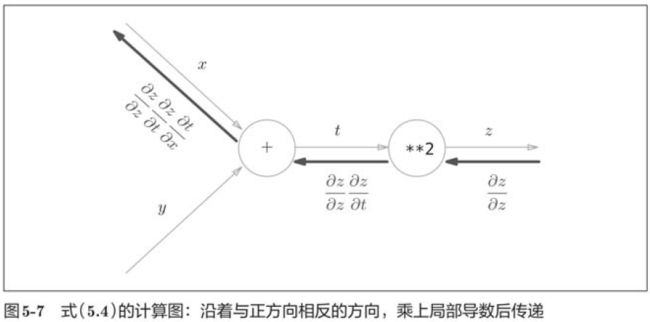
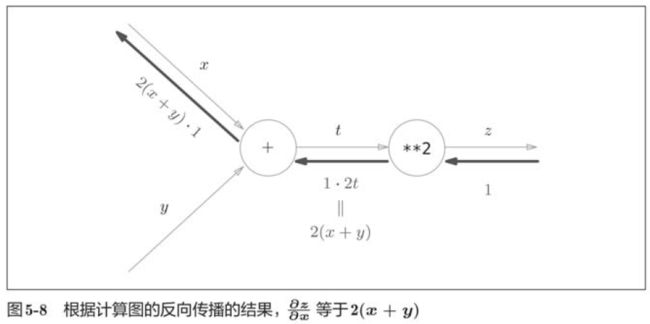
如图所示，计算图的反向传播从右到左传播信号。反向传播的计算顺序是，先将节点的输入信号乘以节点的局部导数（偏导数），然后再传递给下一个节点。

5.3 反向传播

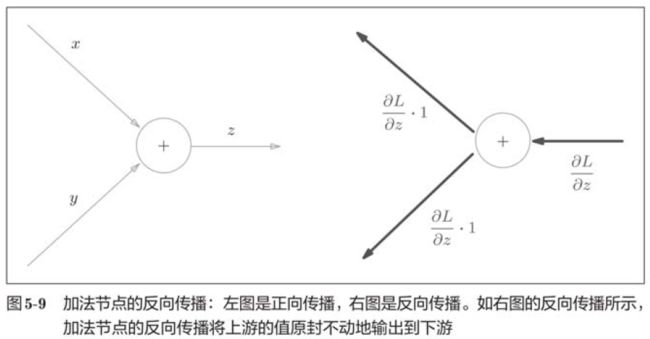
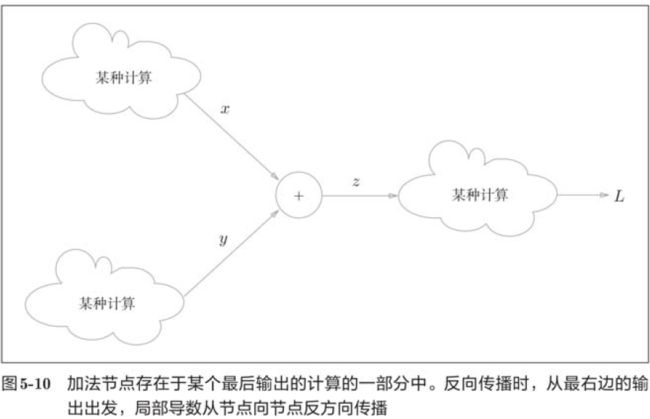
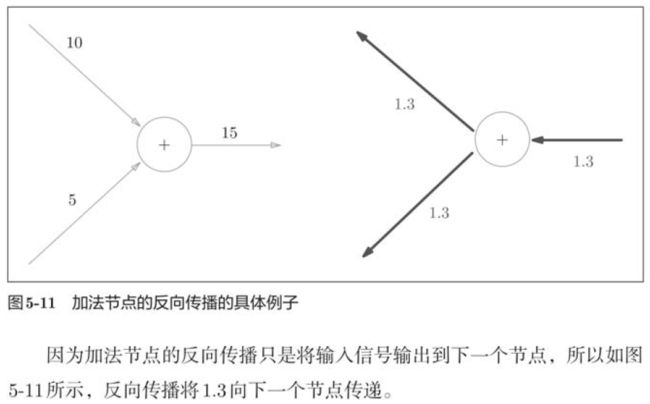
5.3.1 加法节点的反向传播 

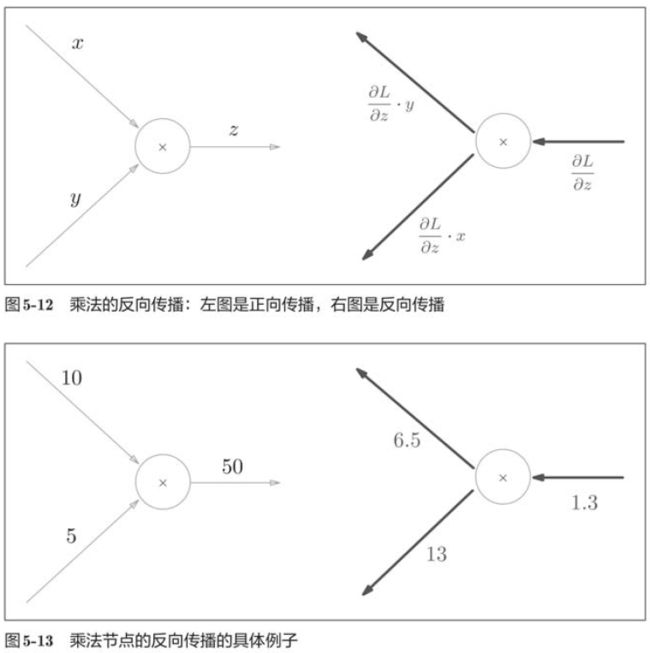
5.3.2 乘法节点的反向传播

加法的反向传播只是将上游的值传给下游，并不需要正向传播的输入信号，但是，乘法的反向传播需要正向传播时的输入信号值。因此，实现乘法节点的反向传播，要保存正向传播的输入信号。

5.3.3 苹果的例子

5.4 简单层的实现

这里，我们把要实现的计算图的乘法节点称为“乘法层”，加法节点称为“加法层” 。

5.4.1 乘法层的实现

层的实现中有两个共同的方法（接口）forward()和backward()。forward()对应正向传播，backward()对应反向传播。

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy

    

上面就是MulLayer的实现。

使用这个乘法层的话，上图中的正向传播可以像下面这样实现：

apple = 100
apple_num = 2
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)

print(price)

220.00000000000003

此外，关于各个变量的导数可由backward()求出。

# backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)
print(dapple, dapple_num, dtax)

2.2 110.00000000000001 200

5.4.2 加法层的实现

接下来，我们实现加法节点的加法层，如下所示：

class AddLayer:
    def __init__(self):
        pass
    
    def forward(self, x, y):
        out = x + y
        return out
    
    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1
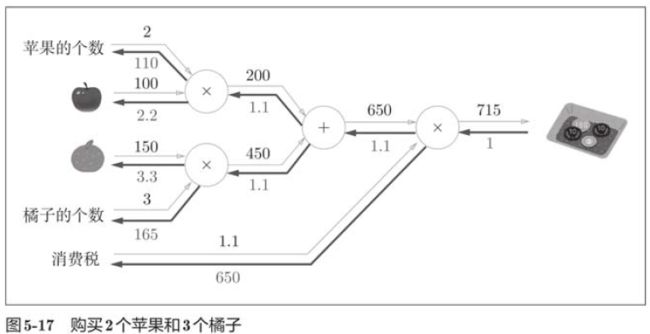
        return dx, dy

现在，我们使用加法层和乘法层，实现购买2个苹果和3个橘子的例子。

apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
orange_price = mul_orange_layer.forward(orange, orange_num)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)
price = mul_tax_layer.forward(all_price, tax)

# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print('price:', int(price))
print('dApple:', dapple)
print('dApple_num:', int(dapple_num))
print('dOrange:', dorange)
print('dOrange_num:', int(dorange_num))
print('dTax:', dtax)

price: 715
dApple: 2.2
dApple_num: 110
dOrange: 3.3000000000000003
dOrange_num: 165
dTax: 650

5.5 激活函数层的实现

5.5.1 ReLu层

激活函数ReLU由下式表示：

求出y关于x的导数为：

class Relu:
    def __init__(self):
        self.mask = None
        
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
    
        return out
    
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        
        return dx

ReLU层的作用就像电路中的开关一样。正向传播时，有电流通过的话，就将开关设为ON；没有电流通过的话，就将开关设为OFF。反向传播时，开关为ON的话，电流会直接通过；开关为OFF的话，则不会有电流通过。

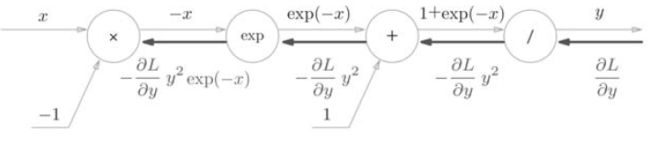
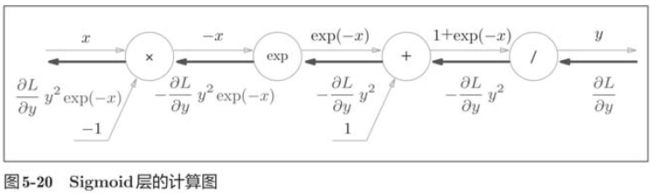
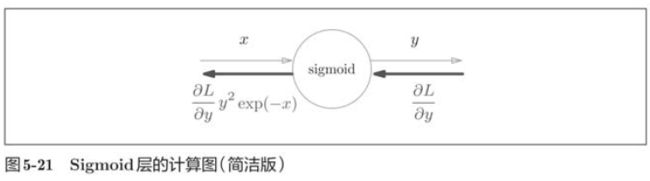
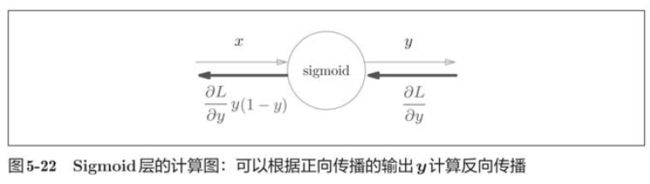
5.5.2 Sigmoid层

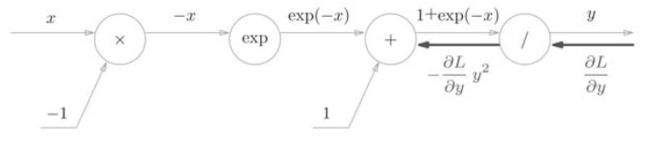
接下来，我们来实现sigmoid函数。

 反向传播的流程：

步骤1

步骤2

 步骤3

步骤4

class Sigmoid:
    def __init__(self):
        self.out = None
        
    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        
        return dx

 5.6 Affine/Softmax层的实现

5.6.1 Affine层

5.6.2 批版本的Affine层

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None
    
    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        
        return out
    
    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        return dx

5.6.3 Softmax-with-Loss层 

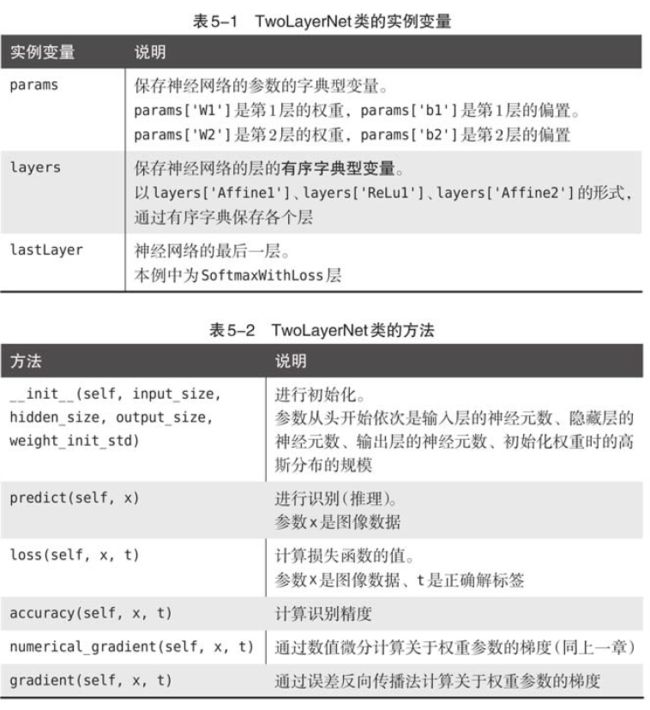
神经网络中进行的处理有推理和学习两个阶段。神经网络的推理通常不使用Softmax层，当神经网络的推理只需要给出一个答案的情况下，因为此时只对得分最大值感兴趣，所以不需要Softmax层。不过，神经网络的学习阶段则需要Softmax层。

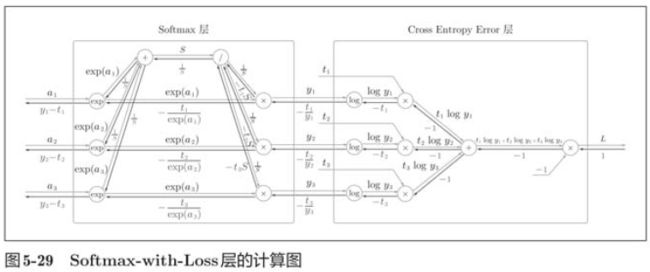
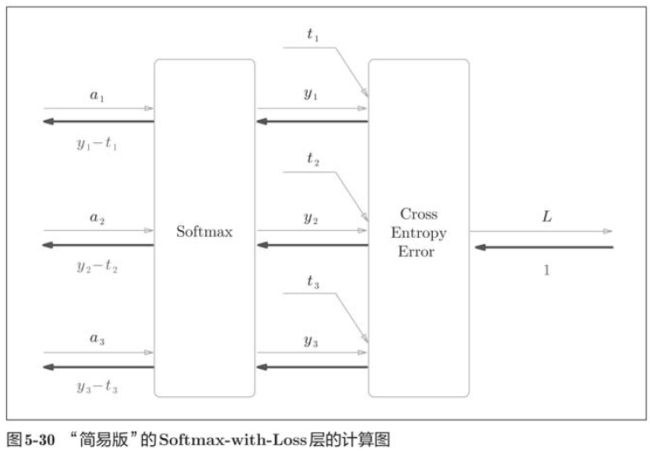 神经网络学习的目的就是通过调整权重参数，使神经网络的输出接近监督标签。因此，必须将神经网络的输出与监督标签的误差高效地传递给前面的层。

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None
        self.t = None
    
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss
    
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        
        return dx

5.7 误差反向传播法的实现

5.7.1 神经网络学习的全貌图

5.7.2 对应误差反向传播法的神经网络的实现 

import os
import sys
sys.path.append(os.pardir)
import numpy as np
from layers import *
from gradient import numerical_gradient
from collections import OrderedDict


class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size,)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'],self.params['b2'])
        self.lastLayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=t)
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastlayer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['b1'] = self.layers['Affine1'].db
        grads['W2'] = self.layers['Affine2'].dW
        grads['b2'] = self.layers['Affine2'].db

        return grads

5.7.3 误差反向传播法的梯度确认

数值微分的优点是实现简单，因此，一般情况下不太容易出错。而误差反向传播法的实现很复杂，容易出错。所以，经常会比较数值微分的结果和误差反向传播法的结果，以确认误差反向传播法的实现是否正确。确认数值微分求出的梯度结果和误差反向传播法求出的结果是否一致（严格地讲，是非常相近）的操作称为梯度确认。

import sys
import os
sys.path.append(os.pardir)
import numpy as np
from mnist import load_mnist
from two_layers import TwoLayerNet

(x_train, y_train), (x_test, y_test) = load_mnist(normailize=True, one_hot_label True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
x_batch = x_train[:3]
t_batch = t_train[:3]

grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backrop = network.gradient(x_batch, t_batch)

for key in grad_numerical.keys():
    diff = np.average(np.abs(grad_backprop[key] - grad_numerical[key]))
    print(key + ":" + str(diff))
    

 5.7.4 使用误差反向传播法的学习

import sys
import os
sys.path.append(os.pardir)
import numpy as np
from mnist import load_mnist
from two_layer_net import TwoLayerNet


(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    # 通过误差反向传播法求梯度
    grad = network.gradient(x_batch, t_batch)

    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

        loss = network.loss(x_batch, t_batch)
        train_loss_list.append(loss)

        if i % iter_per_epoch == 0:
            train_acc = network.accuracy(x_train, t_train)
            test_acc = network.accuracy(x_test, t_test)
            train_acc_list.append(train_acc)
            test_acc_list.append(test_acc)
            print(train_acc, test_acc)

5.8 小结

本章我们介绍了将计算过程可视化的计算图，并使用计算图，介绍了神经网络中的误差反向传播法，并以层为单位实现了神经网络中的处理。我们学过的层有ReLU层、Softmax-with-Loss层、Affine层、Softmax层等，这些层中实现了forward和backward方法，通过将数据正向和反向地传播，可以高效地计算权重参数的梯度。通过使用层进行模块化，神经网络中可以自由地组装层，轻松构建出自己喜欢的网络。

1.通过使用计算图，可以直观地把握计算过程；

2.计算图的节点是由局部计算构成的，局部计算构成全局计算；

3.计算图的正向传播进行一般的计算，通过计算图的反向传播，可以计算各个节点的导数；

4.通过神经网络的组成元素实现为层，可以高效地计算梯度（反向传播法）；

5.通过比较数值微分和误差反向传播法的结果，可以确认误差反向传播法的实现是否正确（梯度确认）。