七大排序详解（选择、插入、冒泡、希尔、归并、快速、堆）- Java实现

本文图片来自
https://www.jianshu.com/p/d243e1aa13ce

一张图概述各种常用的排序算法：

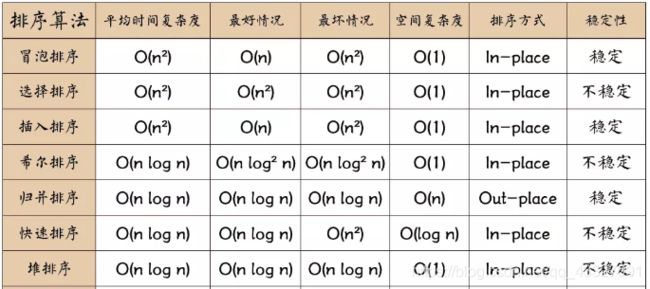
下列代码都是各种排序的核心代码

一、冒泡排序

1.1 算法思想

每轮都会将剩余序列中最大值或者最小值得出，直到剩余一个数字

1.2 动画演示

1.3 代码实现

	/**
	 * 冒泡排序
	 * 外层控制轮数：n-1轮
	 * 内层控制比较次数：n-i-1次
	 */
	public static void sort(int[] array) {
	    int len = array.length;
	    for (int i = 0; i < len - 1; i++) {
	        for (int j = 0; j < len - i - 1; j++) {
	            if (array[j] > array[j+1]) {
	                int temp = array[j];
	                array[j] = array[j+1];
	                array[j+1] = temp;
	            }
	        }
	    }
	}

二、选择排序

2.1 算法思路

每轮将序列中最大或者最小值依次放到数组前面

2.2 动画演示

2.3 代码实现

	/**
	 * 选择排序
	 * 遍历数组每次将最小的数与数组第一位交换，依次类推
	 */
	public static void sort(int[] array) {
	    int len = array.length;
	    for (int i = 0; i < len; i++) {
	        // 记录最小元素的下标
	        int min = i;
	        for (int j = i+1; j < len; j++) {
	            if (array[min] > array[j]) {
	                min = j;
	            }
	        }
	        int temp = array[min];
	        array[min] = array[i];
	        array[i] = temp;
	    }
	}

三、插入排序

3.1 算法思路

每轮选取前n位数字，使该序列有序

3.2 动画演示

3.3 代码实现

	/**
	 * 直接插入排序
	 * 记录第i位数字，如果前面的大于该数字，那么直接覆盖后一位，
	 * 否则跳出循环，循环结束第j位为数字插入的位置
	 */
	public static void sort(int[] array) {
	    int len = array.length;
	    for (int i = 1; i < len; i++) {
	        int temp = array[i];
	        int j;
	        for (j = i; j > 0 && array[j-1] > temp; j--) {
	            array[j] = array[j-1];
	        }
	        array[j] = temp;
	    }
	}

四、希尔排序

希尔排序算是插入排序的一种优化
由于递增序列会影响希尔排序的效率，目前还未的到一个完美的递增序列，所以希尔排序的时间复杂度上限难以计算，一般递增序列互质比较好

4.1 算法思路

根据递增序列{h1,h2,h3,…,1}，每次保证间隔为h的序列有序，直到h递减到1，得到有序序列

4.2 动画演示

4.3 代码实现

下面代码使用递增序列 （h = 3*h + 1）

	/**
	 * 希尔排序
	 * 该算法使用的增量序列为：3*h+1 (1, 4, 13, 40, 121, 364, ...)
	 * 每次保证间隔为h的序列有序，h递减到1，而每个h序列排序，就是插入排序，只是步长为h
	 */
	public static void sort(int[] array) {
	    int len = array.length;
	    int h = 1;
	    while (h < len/3)
	        h = 3*h + 1;
	
	    while (h >= 1) {
	        for (int i = h; i < len; i++) {
	            int temp = array[i];
	            int j;
	            for (j = i; j >= h && temp < array[j-h]; j -= h)
	                array[j] = array[j-h];
	            array[j] = temp;
	        }
	        h /= 3;
	    }
	}

五、归并排序

5.1 算法思路

将序列采用分治的思想，递归分为多段序列，直到成单，然后合并多段序列保证两两有序

5.2 动画演示

下面代码使用的自顶向下的归并排序，当然还有自底向上的方法可以自行研究

5.3 代码实现

	/**
     * 辅助数组
     */
    public static int[] temp;
    public static void sort(int[] array, int left, int right) {
        if (left >= right)
            return;
        int mid = (left + right) / 2;
        sort(array, left, mid);
        sort(array, mid + 1, right);
        merge(array, left, mid, right);
    }

    /**
     * 归并两个序列
     */
    public static void merge(int[] array, int left, int mid, int right) {
        int i = left, j = mid + 1;

        for (int k = left; k <= right; k++)
            temp[k] = array[k];

        for (int k = left; k <= right; k++) {
            if (i > mid)
                array[k] = temp[j++];
            else if (j > right)
                array[k] = temp[i++];
            else if (temp[i] < temp[j])
                array[k] = temp[i++];
            else
                array[k] = temp[j++];
        }
    }

六、快速排序

6.1 算法思路

每段序列选取最左边为标志值，左边的比标记值小，右边的比标记值大，每次递归会将标记值放到最终位置

6.2 动画演示

6.3 代码实现

	/**
     * 快速排序
     * 以最左边为标记值，每次递归会使标记为置于最终位置
     */
    public static void sort(int[] array, int left, int right) {
        if (left > right)
            return;
        int i = left, j = right, temp = array[left], t;
        while (i != j) {
            while (array[j] >= temp && i < j)
                j--;
            while (array[i] <= temp && i < j)
                i++;
            if (i < j) {
                t = array[i];
                array[i] = array[j];
                array[j] = t;
            }
        }
        array[left] = array[i];
        array[i] = temp;

        sort(array, left, i-1);
        sort(array, i+1, right);
    }

七、堆排序

7.1 算法思路

将起始无序序列构建成堆，那么堆顶元素就为该序列的最大值或最小值，每次交换最后一个元素和堆顶元素（去掉堆顶元素），剩余序列重新进行堆调整

7.2 动画演示

7.3 代码实现

	/**
     * 堆排序
     * 1.将一个无序序列构建成一个堆
     * 2.每次输出堆顶元素后，调整剩余元素成为一个新的堆
     */
    public static void sort(int[] array) {
        int n = array.length;

        // 将一个无序序列构建成一个堆
        for (int i = (n-1)/2 - 1; i >= 0; i--)
            heapify(array, i, n-1);

        // 每次将堆顶元素出堆，并剩余元素成为新的堆
        for (int i = n-1; i > 0; i--) {
            int temp = array[0]; array[0] = array[i]; array[i] = temp;
            n--;
            heapify(array, 0, n-1);
        }
    }
    /**
     * 堆调整
     */
    public static void heapify(int[] array, int s, int m) {
        while (2*s+1 <= m) {
            // 左孩子结点下标
            int left = 2*s+1;
            // 右孩子结点下标
            int right = 2*s+2;
            // 记录根、左子、右子三个结点中最大结点下标
            int largest = s;
            // 如果左子结点大于根结点
            if (left <= m && array[left] > array[largest])
                largest = left;
            if (right <= m && array[right] > array[largest])
                largest = right;
            // 其中一个孩子结点大于根结点，就交换
            if (largest != s) {
                int temp = array[largest]; array[largest] = array[s]; array[s] = temp;
            } else
                break;
            // 继续对交换之后的孩子结点向下调整
            s = largest;
        }
    }