算法竞赛入门经典(第2版)—第六章(数据结构基础)
文章目录
-
-
-
- 零碎知识点整理
- 题目
-
- 210 - Concurrency Simulator
- 514 - Rails
- 442 - Matrix Chain Multiplication
- 11988 - Broken Keyboard (a.k.a. Beiju Text)
- 12657 - Boxes in a Line
- 679 - Dropping Balls
- 122 - Trees on the level
- 548 - Tree
- 839 - Not so Mobile
- 699 - The Falling Leaves
- 297 - Quadtrees
- 572 - Oil Deposits
- 1103 - Ancient Messages
- 816 - Abbott's Revenge
- 10305 - Ordering Tasks
- 10129 - Play on Words
- 10562 - Undraw the Trees
- 12171 - Sculpture
- 1572 - Self-Assembly
- 1599 - Ideal Path
- 506 - System Dependencies
- 11853 - Paintball
- 673 - Parentheses Balance
- 712 - S-Trees
- 536 - Tree Recovery
- 439 - Knight Moves
- 1600 - Patrol Robot
- 12166 - Equilibrium Mobile
- 10410 - Tree Reconstruction
- 12118 - Inspector's Dilemma
-
-
零碎知识点整理
- fill和memset函数。参考博文:【C++】fill函数,fill与memset函数的区别
- fill的头文件为
#include。可以将数组或容器赋任何值。- 对于数组:fill(arr, arr + n, 要填入的内容);
- 对于容器:fill(v.begin(), v.end(), 要填入的内容);
- memset的头文件为
#include。只能为int类型数组的赋值为0或-1。- 对于数组:memset(a, 0, sizeof(a))。
初始化赋值为非0的int数组或容器,推荐使用fill。
- fill的头文件为
- 欧拉回路:从图中一个点出发走出一条路,每条边恰好经过一次。判断欧拉道路的条件:
- 无向图:1.无向图连通。2.最多有两个度数为奇数的点。
- 当度数均为偶数时,为欧拉回路。
- 有向图:1.忽略边的方向后,有向图连通。2.最多有两个入度不等于出度,其中一个多1,另一个少1。多1的为起始点,少1的为终止点。
- 当入度均等于出度时,为欧拉回路。
- 无向图:1.无向图连通。2.最多有两个度数为奇数的点。
- freopen(“input.txt”,“r”,stdin);用来读取程序输入文件,使得文件的输入输出分开,更好调试。头文件为stdio.h。参考博文:
freopen(“in.txt”,“r”,stdin) 函数的用法
#ifdef ONLINE_JUDGE
#else
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
#endif
- 当图中结点之间可能有多个边相连时,必须使用邻接表来存储,而不能使用邻接矩阵。
- find函数:参考
-
头文件:
#include -
find函数的表示:
- 一般表示:find(start,end,value)。start搜寻的起点,end搜寻的终点,要寻找的value值。
- 容器表示:find(a.begin(),a.end(),value)。
- 数组表示:find(a,a+length,val)。
所有的返回,均是迭代器(容器)或指针(数组),而非是直观感觉上的索引下标。如果在查找范围内不存在,返回a.end(),这里需要注意的是,a.end()不在查找范围内。
-
各个容器自己实现的find成员函数:
- vector没有实现find函数,除此之外,常见容器都实现了自己的find函数。
- String是这一种顺序存储结构,其find函数返回的是下标索引。set,map,multiset,multimap都不是顺序索引的数据结构,所以返回的是迭代器。
-
判断元素是否存在。
- 对于返回迭代器的查找,通过判断find(a.begin(),a.end(),value)==a.end(),来判断元素是否存在。
- 对于string,通过a.find(val)==string::npos判断。
-
题目
210 - Concurrency Simulator
题目链接:210 - Concurrency Simulator
参考博文:uva 210 - Concurrency Simulator (并行程序模拟)
- 题目大意:题目比较复杂。
- 思路:大模拟题,细节比较多。详见代码。
代码:
#include514 - Rails
题目链接:514 - Rails
- 题目大意:火车按序进栈,给定火车出栈的顺序,问火车能否按照这个顺序出栈。
- 思路:简单的栈应用,序号每次入栈后,均需要判断栈顶是否与当前出栈序号相同,相同则出栈,然后继续判断栈顶与下一个序号是否相同,如此循环,不相同则继续按序进栈。
代码:
#include 442 - Matrix Chain Multiplication
题目链接:442 - Matrix Chain Multiplication
- 题目大意:输入一些矩阵乘法式子,有括号。求矩阵相乘需要的加法步数。
- 思路:简单栈模拟。先建立一个映射map,将字母与结构体(包括行和列)对应,然后遍历式子,遇到字母,将其对应的结构体入栈;遇到’)'将其栈顶的两个结构体计算一下,并计算出新的结构体,入栈,直到栈为空。
代码:
#include 11988 - Broken Keyboard (a.k.a. Beiju Text)
题目链接:11988 - Broken Keyboard (a.k.a. Beiju Text)
- 题目大意:你有一个破损的键盘,键盘上所有的键都可以正常工作,但有时Home键和End键会自动按下,你不知道键盘存在这样的问题,当你输入完成以后屏幕上显示的是一串混乱的文本,你的任务是要输出这段混乱的文本是什么。
多组输入,每组输入一行字符串,其中 ‘[ ’ 代表Home键,’ ]’代表End键
每组数据输出一行,即在屏幕上显示的文本。 - 思路:STL中list的使用。注意迭代器指向的是特定元素,要与数组下标区分开来,list.insert(it, ch)表示在it指向的元素前面添加元素。思路就是模拟题意即可。
代码:
#include
using namespace std;
list<char> s;
char ch;
int main()
{
int flag = 1, cnt = 0;
list<char>::iterator it;
while(ch=getchar())
{
if(ch==EOF) break;
if(ch=='\n')
{
for(it=s.begin(); it!=s.end(); it++)
printf("%c", *it);
printf("\n");
s.clear();
}
else if(ch==']') cnt = s.size();
else if(ch=='[') cnt = 0;
else
{
if(cnt==0)//当前面一个字符是'['
{
it = s.begin();//迭代器移到最前面
s.push_front(ch);
}
else if(cnt==s.size())//当遇到[后或初始状态
{
s.push_back(ch);//在字符串后面添加
}
else
{
s.insert(it, ch);//在it指向的元素(原首部元素)的前方插入元素
}
cnt++;
}
}
return 0;
}
12657 - Boxes in a Line
题目链接:12657 - Boxes in a Line12657 - Boxes in a Line
- 题目大意:開始有n个盒子按1到n的顺序排列 对这些盒子进行m次操作 每次为把x移到y的左边 、右边、交换x,y 颠倒顺序中的一个。求操作完毕后全部奇数位原盒子序号的和。
- 思路:一个链表模拟题,不能使用STL中的list,因为无法在O(1)复杂度下定位到某一个位置。本题目有一定的技巧,比如记录翻转的奇偶性。奇偶性不同操作不同。
代码:
#include 679 - Dropping Balls
题目链接:679 - Dropping Balls
- 题目大意:有一棵二叉树,最大深度为D,且所有叶子的深度都相同。所有结点从上到下从左到右编号为1, 2, 3,…, 2D-1。在结点1处放一个小球,它会往下落。每个内结点上都有一个开关,初始全部关闭,当每次有小球落到一个开关上时,状态都会改变。当小球到达一个内结点时,如果该结点上的开关关闭,则往左走,否则往右走,直到走到叶子结点,如图6-2所示。
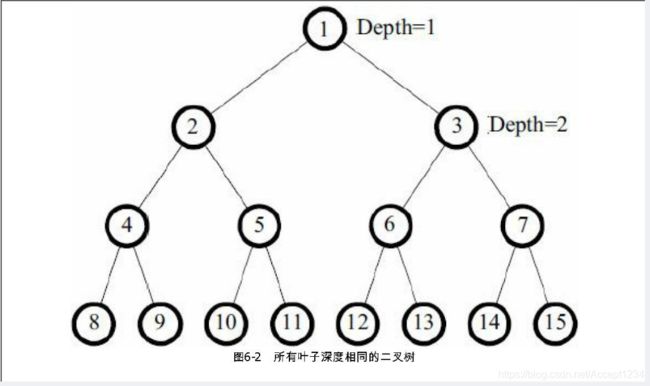
一些小球从结点1处依次开始下落,最后一个小球将会落到哪里呢?输入叶子深度D和小球个数I,输出第I个小球最后所在的叶子编号。假设I不超过整棵树的叶子个数。D≤20。输入最多包含1000组数据。 - 思路:本题目看似简单,可以快速使用模拟法模拟,但是数据量太大,导致模拟法超时。所以参考了书本上面的算法,对于到达当前节点的小球,如果第I个小球是第奇数个到达的,那么它应该向左走,同时也是第(I+1)/2个向左走的,如果是偶数个,应该向右走,同时也是第I/2个向右走的。然后当前节点k的左节点是2k,右节点是2k+1,不断循环直到循环深度为D为止即可。
直接模拟(超时)代码:
#include AC代码:
#include 122 - Trees on the level
题目链接:122 - Trees on the level
-
题目大意:输入一棵二叉树,你的任务是按从上到下、从左到右的顺序输出各个结点的值。每个结点都按照从根结点到它的移动序列给出(L表示左,R表示右)。在输入中,每个结点的左括号和右括号之间没有空格,相邻结点之间用一个空格隔开。每棵树的输入用一对空括号“()”结束(这对括号本身不代表一个结点),如图6-3所示。
注意,如果从根到某个叶结点的路径上有的结点没有在输入中给出,或者给出超过一次,应当输出-1。结点个数不超过256。
样例输入:
(11,LL) (7,LLL) (8,R) (5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()
(3,L) (4,R) ()
样例输出:
5 4 8 11 13 4 7 2 1
not complete -
思路:我使用了模拟法。对于"LR"的路径,"L"代表序号乘以2,"R"代表序号乘以2+1。然后使用map将序号与编号映射起来,在使用set存储所有序号。如果序号重复或父节点不存在,则表明该树不存在,否则按序号顺序输出编号即可。
代码:
#include 书中的代码:
#include 548 - Tree
题目链接:548 - Tree
- 题目大意:根据树的中序和后序遍历,求出其从路径到达叶子节点权值最小的叶子节点,当路径权值和相等时,取自身权值小的叶子节点。
- 思路:根据中序和后序建立二叉树后,深度优先遍历即可。
代码:
#include 839 - Not so Mobile
题目链接:839 - Not so Mobile
代码:
#include 699 - The Falling Leaves
题目链接:699 - The Falling Leaves
- 题目大意:给一棵二叉树,每个结点都有一个水平位置:左子结点在它左边1个单位,右子结点在右边1个单位。从左向右输出每个水平位置的所有结点的权值之和。如图6-7所示,从左到右的3个位置的权和分别为7,11,3。按照递归(先序)方式输入,用-1表示空树。

样例输入:
5 7 -1 6 -1 -1 3 -1 -1
8 2 9 -1 -1 6 5 -1 -1 12 -1 -1 3 7 -1 -1 -1
-1
样例输出:
Case 1:
7 11 3
Case 2:
9 7 21 15
- 思路:采用了递归输入,技巧性应用。同时还需要选择出根节点的位置。
代码:
#include 297 - Quadtrees
题目链接:297 - Quadtrees
- 题目大意:如图所示,可以用四分树来表示一个黑白图像,方法是用根结点表示整幅图像,然后把行列各分成两等分,按照图中的方式编号,从左到右对应4个子结点。如果某子结点对应的区域全黑或者全白,则直接用一个黑结点或者白结点表示;如果既有黑又有白,则用一个灰结点表示,并且为这个区域递归建树。

给出两棵四分树的先序遍历,求二者合并之后(黑色部分合并)黑色像素的个数。p表示中间结点,f表示黑色(full),e表示白色(empty)。
样例输入:
3
ppeeefpffeefe
pefepeefe
peeef
peefe
peeef
peepefefe
样例输出:
There are 640 black pixels.
There are 512 black pixels.
- 思路:与上面两道题类似,只不过需要使用数组记录一下,方便累加。
代码:
#include 572 - Oil Deposits
题目链接:572 - Oil Deposits
- 题目大意: 在一个字符矩阵中,计算@连通块的数量。
- 思路:dfs简单题,遍历+dfs。
代码:
#include 1103 - Ancient Messages
题目链接:1103 - Ancient Messages
- 题目大意:输入一些十六进制的矩阵,将它转换为二进制后,根据01的形状寻找相应字符,具体细节看原题。
- 思路:这道题目思路比较巧妙,不同字符的区别仅在于其中围起来圈圈的个数。但需要注意在遍历前需要为其外围再围上一圈’0’,防止最外围是’1’。而得到圈圈的方法是,遍历为每一个相邻相等的字符打上相同的编号,非0编号的’0’一定是围起来的’0’。通过遍历不同编号’1’周围’0’的编号种类数目,可以得到圈圈的个数。具体细节详见代码。
代码:
#include 816 - Abbott’s Revenge
题目链接:816 - Abbott’s Revenge
- 题目大意:迷宫从起点走到终点,进入某点的朝向不同,可以出去的方向也不同,输出最短路经。
- 思路:一个bfs的变体,思想不难,就是代码量比较大,使用了较多的数据结构。
当代码量比较大时,一定要注意细节,伪代码要详细,思考要缜密,代码量虽然大,但要清清楚楚。
代码:
#include 10305 - Ordering Tasks
题目链接:10305 - Ordering Tasks
拓扑排序的两种方法:UVA - 10305 Ordering Tasks(拓扑排序模板题)
- 题目大意: 给出n组二元数据,前面的的序号表示这个任务先于后面序号的任务,要求将任务先后排序(不一定有一种)。
- 思路:典型的拓扑排序题目。拓扑排序思想是每一次选择入度为0的点,然后删去其所有出度边,这样不断迭代,直到所有点均被选择。本题使用了队列来存储入度为0的点,不断更新队列,直到将所有的点遍历。
代码:
#include 使用dfs的拓扑排序:
#include10129 - Play on Words
题目链接:10129 - Play on Words
- 题目大意:输入一些单词,使得这些单词可以根据首尾字母连接成串,即一个单词的尾字母要与另一个单词的首字母相同。判断是否可以连接成串。
- 思路:一个欧拉路径题目。题目可以转换成一个有向图的欧拉路径,因此需要存储每一个结点的出入度数,判断其是否满足欧拉路径的出入度条件。然后使用dfs判断是否可以遍历无向图的所有结点(使用set存储遍历到的结点然后与之前存储的结点比较)。
代码:
#include 10562 - Undraw the Trees
题目链接:10562 - Undraw the Trees
- 题目大意:输入一个多叉树,输出其括号表示法。
- 思路:使用dfs的思想,对每一个子树由左到右深度优先递归遍历即可,我的代码量比较大,大多数用来寻找子树的范围了(即’-'的范围)。
我的代码:
#include 书上的代码:
#include 12171 - Sculpture
题目链接:12171 - Sculpture
参考博文:Sculpture (UVa 12171) bfs + 离散化
- 题目大意:求有多个长方体组成的不规则立方体的体积和外表面积。
- 思路:比较难的题目。先采用了坐标离散化处理(同时在周围加上空气坐标,最大最小的坐标一定不为建筑物),将区域使用坐标表示,然后使用bfs来从空气出发遍历,求得空气内表面积(建筑物外表面积)和空气体积(总体积-建筑物体积)。书上的代码采用了结构体函数,比较精妙,值得学习。
代码:
#include 1572 - Self-Assembly
题目链接:1572 - Self-Assembly
参考博文:UVA ~ 1572 ~ Self-Assembly (拓扑排序)
- 题目大意:有n(n≤40000)种边上带标号的正方形。每条边上的标号要么为一个大写字母后面跟着一个加号或减号,要么为数字00。当且仅当两条边的字母相同且符号相反是,两条边能够拼到一起(00不能和任何边拼在一起,包括另一条标号为00的边)。
假设输入的每种正方形都有无穷多种,而且可以翻转和旋转,你的任务是判断能否组成一个无限大的结构。每条边要么悬空(不喝任何边相邻),要么和一个上述可拼接的边相邻。如图6-17(a)所示是3个正方形,图6-17(b)是他们组成的一个合法结构(但大小有限)。 - 思路:本题看上去很难下手,但不难发现“可以旋转和翻转”是一个很有意思的条件,值得推敲。“无限大结构”并不一定能铺满整个平面,只需要能连出一条无限长的“通路”即可。借助旋转和翻转,可以让这条“通路”总是往右和往下延伸,因此永远不会自交。这样一来,只需要某个正方形为起点开始“铺路”,一旦可以拼上一块和起点一样的正方形,无限重复下去就能得到一个无限大的结构。
可惜这样的分析仍然不够,因为正方形的数目n很大。进一步分析发现:实际上不需要正方形本身重复,而只需要边上的标号重复即可。这样问题就转化为:把标号看成点(一共A+ ~ Z+,A- ~ Z- 这52种,因为00不能作为拼接点),正方形看作边,得到一个有向图。则当且仅当图中存在有向环时有解。只需要做一次拓扑排序即可。
所以本题思考的重点是如何建立有向图。如果将正方形看做边,对于A+B-C+00来说,A+实际上可以与B+,C-相连,B-可以与A-,C-相连,C+可以与A-,B+相连,所以可以根据这个特点在输入序列中将有向图建立起来,然后拓扑排序,有环则表示可以无限大,否则不可以。我的拓扑排序使用的是队列模拟法。参考博文里面使用的是dfs的拓扑排序法。
代码:
#include 1599 - Ideal Path
题目链接:1599 - Ideal Path
- 题目大意:

- 思路:首先从终点开始进行BFS,同时记录从终点开始到每个节点的最短路径的长度,这样一直到起点,然后从起点开始进行新的一轮的BFS,在新的一轮的BFS中,我们要记录所走路径的颜色信息,每次选择颜色最小的那一条路来走,同时要注意,如果从当前的节点开始有多条颜色最小的路径,那么我们要将相应节点的编号都要存到队列当中,在下一轮的时候依次出队列分别进行下一轮的比较,保证所走的路径的颜色值是字典序最小的。
代码:
#include 506 - System Dependencies
题目链接:506 - System Dependencies
参考博文:System Dependencies
- 题目大意:详见原题。
- 思路:一个细节比较多的模拟题(拓扑思想)。主要考虑到有显式安装和隐式安装,还需要维护依赖关系和安装组件的数组,细节详见博文和代码,特点是将组件名称转换为ID数字,方便操作。
代码:
#include11853 - Paintball
题目链接:11853 - Paintball
参考博文:UVA 11853 Paintball
- 题目大意:在1000*1000的区域内,一堆人玩水弹(也许是吧),知道他们的坐标和攻击范围,问你从西边到东边能否不被水弹砸。找出西边进入的最北位置和东边出去的最北位置。
- 思路:这道题的思路和巧妙,分为两个部分。第一个部分是判断能否安全出入,第二个部分是计算出进入和出去的位置。对于第一个部分可以这样想,把整个方形区域看作水面,把禁区看作小岛,如果可以从上边沿着这些小岛走到下边的话,就说明方形区域被禁区整个隔断了,那么就不能从左边走到右边,这样一来DFS即可。对于第二个部分,求东西最北的出入位置,只需要在DFS的时候计算当前禁区与左右边缘的下交点,不断更新坐标值即可。

代码:
#include 673 - Parentheses Balance
题目链接:673 - Parentheses Balance
- 题目大意:输入一行包含()和[]的字符串,检查每对括号是否匹配得上,能就Yes否则No。同时空字符串也看成是符合情况的。
- 思路:简单题栈题目,但是输入需要使用getline,因为可能输入空字符串,cin无法读入。题目中没有说是否考虑空格但是后面的测试样例中有空格,并且还把含空格的样例判断成了正确的,但是我测试后发现无论将含空格的样例判断成正确还是错误,代码均通过。因此说明后台数据没有含空格的数据,但是根据题目意思,确实应该将含空格的样例判断为错误。
代码:
#include 712 - S-Trees
题目链接:712 - S-Trees
- 题目大意:

- 思路:一个简单的关于树的技巧题。需要观察规律,发现其和二进制完全等价,级该二进制(问题字符串)代表的值是叶节点字符串的下标,而且该二进制需要与 x i x_i xi对应,即需要根据 x i x_i xi的顺序重新排列二进制字符串得到新的串,该串对应的二进制的值就是输入的叶节点字符串的下标。
代码:
#include 536 - Tree Recovery
题目链接:536 - Tree Recovery
参考博文:acm之旅–树
- 题目大意:给出树的前序和中序,求其后序。
- 思路:可以根据前序找子树的根节点,然后在中序中划分左右子树,然后就可以根据关系重建树,或者直接得到后序关系。
代码:
#include 439 - Knight Moves
题目链接:439 - Knight Moves
- 题目大意:一个8*8的国际象棋,马从一个位置调到另一个位置,求其最短步数。
- 思路:裸的bfs求最短路径长度。
代码:
#include 1600 - Patrol Robot
题目链接:1600 - Patrol Robot
参考博文:uva1600 Patrol Robot(不同的BFS最短路)
UVA1600-Patrol Robot(BFS进阶)
- 题目大意:在bfs基础上可以最多连续穿越k个障碍,求最短路径长度。
方法一:
- 思路:这道题看似简单,让我使劲浑身解数也没有做出来。
重点在于,如何处理连续穿越k个障碍,有可能物体从两条路到达一个位置,虽然有一条路长度较长,但是可以穿越更多障碍,而另一条虽然先到达,但是因为可以穿越的障碍少,使得无法到达目的地。一种处理方法是:增加一个数组用来存储当前结点还能跨过几个障碍。可以知道,在到达同一个位置时,在步数比之前步数要大的情况下,如果还可以跨越的障碍物没有之前的要多,那么就一点优势就没有了,就可以把这种情况减枝掉。因此每到一个结点,判断当前走法所剩的k值,如果小于当前结点的值(即之前走法有更大的k),就舍弃。
代码:
#include 方法二:
- 思路:这种解决方案是将标记vis数组增加一维,表示穿越了几个障碍物到达这里,这样再去判重减枝。这种方法仅减去了在穿越同样障碍物是到达同一个位置步数比较大的情况,没有减去在穿越更多的障碍物得到同一个位置步数比较大的情况。
因此,我的改进方法是如果当前是第一个到达该位置的,那么就将经过更多(包括与当前情况一样的)障碍物的vis数组全部赋值为1,即以后只能在穿越更少的障碍物的情况下访问该位置(因为走的步数更多)。
代码:
#include 12166 - Equilibrium Mobile
题目链接:12166 - Equilibrium Mobile
- 题目大意:题目大意:给出一棵二叉树,整个树是天平,每个结点有一个砝码或一个天平,对于任意一个天平,绳子都在中点,每个砝码都有重量,求最少修改多少个砝码的重量使得整个天平平衡。
- 思路:本题的难点一方面在与一个想法和题目数据范围。由于要求修改最少的砝码,所以必定会以一个砝码作为参照,或者说该砝码质量不变。即先求出砝码质量的众数,但是要考虑不同深度的砝码,所以需要将因为深度为1的砝码质量为4和深度为2的砝码质量为2本质上是一种情况,所以需要将砝码质量除以pow(2,(树的最大深度-该砝码的深度)),然后求砝码质量的众数,最后砝码总数量减去众数的个数即可。
代码:
#include 10410 - Tree Reconstruction
题目链接:10410 - Tree Reconstruction
参考博文:随缘&不屈UVA10410-Tree Reconstruction(BFS序和DFS序的性质)
UVA10410 TreeReconstruction 树重建 (dfs,bfs序的一些性质,以及用栈处理递归 )
uva 10410 - Tree Reconstruction(栈)
- 题目大意:给出一颗树的BFS和DFS遍历序列,求每一个结点的子结点。
- 思路:一道好题,并且还是比较难。经过思考,首先需要明确:
- 1.在BFS序中,与点a相邻的下一个点可能有三种身份:(1)节点a的孩子 (2)节点a的第一后兄弟 (3)节点a的兄弟的孩子
- 2.在DFS序中,与点a相邻的下一个点可能有三种身份:(1)节点a的孩子(2)节点a的第一后兄弟(3)啥也不是(意思是说直接回到父辈及以上了)
- 当满足DFS序列中相邻(即dfs(v)=dfs(u)+1),如果v和u在BFS中不相邻,且bfs(v)>bfs(u)+1,则表明v是u的子节点,如果v和u在BFS中相邻,且bfs(v)=bfs(u)+1,v
- 当在DFS序列中不相邻(即dfs(v)>dfs(u)+1),则v可能是u的子节点(u有多个子节点),或u的兄弟节点(u有多个兄弟节点),或什么也不是。则此时情况其实跟上一种一样,满足上面的条件,u一定是v的父节点,并且u在DFS中的位置一定比v靠前。
- 还要注意一个细节就是栈顶元素时root时,直接加孩子,入栈。
代码:
#include 12118 - Inspector’s Dilemma
题目链接:12118 - Inspector’s Dilemma
参考博文:UVa 12118 - Inspector’s Dilemma
- 题目大意: 一个有v个顶点的完全图,找一条经过m条指定边的最短路径。
- 思路:欧拉回路的变形题。在每一个连通块中计算奇数端点个数x,然后(x-1)/2就是额外需要走的道路,再加上每个连通块之间要走的道路与必须要走的道路就是走的最少的道路。
代码:
#include 