Path signature介绍
path signature
path signture是描述path的一种特征,它已经在模式识别、异常行为检测、手写识别等领域得到了广泛的运用。现给出path signature的介绍如下:
path
path被定义为一个将连续取值区间[a,b]转换到多维空间 R d R^d Rd的映射。其最简单的理解就是物体运动的轨迹,假定物体在二维平面上从 t 1 t_1 t1时刻持续运动到 t 2 t_2 t2时刻,每个时刻的位置都可以用一二维向量表示,这一轨迹就构成了一条path, X : [ t 1 , t 2 ] ↦ R 2 , X t = { X t 1 , X t 2 } X:[t_1,t_2]\mapsto R^2,X_t=\{X^1_t,X^2_t\} X:[t1,t2]↦R2,Xt={Xt1,Xt2},它的每个维度都表示了物体在对应方向上随时间变化的规律。
import matplotlib.pyplot as plt
import numpy as np
t=np.arange(0,2,0.002)
x=2*t+0.1
y=3*t**2
plt.plot(x,y)
plt.grid(True)
plt.xlabel('$X^1_t$')
plt.ylabel('$X^2_t$')

如上即为一个 X t = 2 t + 0.1 , 3 t 2 X_t={2t+0.1,3t^2} Xt=2t+0.1,3t2的path。
更一般的,path可以表示为:
X : [ a , b ] ↦ R d , X t = { X t 1 , X t 2 . . . X t d } X:[a,b]\mapsto R^d,X_t=\{X^1_t,X^2_t...X^d_t\} X:[a,b]↦Rd,Xt={Xt1,Xt2...Xtd}
在实际应用中,我们能够获得的path通常并不是连续的,而是它在取值区间内的不均匀采样,因此我们通常需要进行不同的插值以获得时间上分布均匀且更加密集的path。
path integral
path sigature实际上是path不同阶路径积分(path integral)的集合,我们首先来介绍路径积分。假定存在两个一维path X t , Y t X_t,Y_t Xt,Yt,且记 X t ′ = d X t / d t X'_t=dX_t/d_t Xt′=dXt/dt,则我们定义路径积分为:
∫ a b Y t X t ′ d t = ∫ a b Y t d X t \int_a^bY_tX'_tdt=\int_a^bY_tdX_t ∫abYtXt′dt=∫abYtdXt
其意义就是在参变量由a变换至b时 Y t Y_t Yt对 X t X_t Xt的积分,这一形式的路径积分是后续所有阶路径积分的基础。
路径积分有着两个非常重要的性质:
-
平移不变性。从路径积分的几何意义我们可以看出其结果实际上是由 Y t , X t Y_t,X_t Yt,Xt之间的相对关系所唯一确定的,与积分变量 X t X_t Xt的初始值 X a X_a Xa并没有什么关系。也就是说如果我们在 X t − t X_t-t Xt−t平面内进上下平移,并不会对积分值产生任何的影响,给出数学描述如下:
∫ a b Y t d X t = ∫ a b Y t d Z t , Z t = X t + c \int^b_aY_tdX_t=\int_a^bY_tdZ_t, Z_t=X_t+c ∫abYtdXt=∫abYtdZt,Zt=Xt+c -
重参数不变性。同样是从路径积分的几何意义出发,结果只和 Y t , X t Y_t,X_t Yt,Xt的相对关系有关,而与参变量 t t t没有关系。假定一条path的参变量由 a a a变化至 b b b时, Y t , X t Y_t,X_t Yt,Xt从 [ Y 0 , X 0 ] [Y_0,X_0] [Y0,X0]变化到 [ Y 1 , X 1 ] [Y_1,X_1] [Y1,X1],而存在另一条path的参变量由 a a a变化至 2 b 2b 2b时, Y t , X t Y_t,X_t Yt,Xt也从 [ Y 0 , X 0 ] [Y_0,X_0] [Y0,X0]变化到 [ Y 1 , X 1 ] [Y_1,X_1] [Y1,X1],这两条Path的路径积分实际上没有区别,即路径积分和 X t X_t Xt的瞬时速度无关。数学描述如下:
∫ a b Y t d X t = ∫ k 1 a k 2 b Y r d X r w h e r e Y t ( X t ) = Y r ( X r ) , X t ( a ) = X r ( k 1 a ) , X t ( b ) = X r ( k 2 b ) \int_a^bY_tdX_t=\int_{k_1a}^{k_2b}Y_rdX_r\\ where\qquad Y_t(X_t)=Y_r(X_r),X_t(a)=X_r(k_1a),X_t(b)=X_r(k_2b) ∫abYtdXt=∫k1ak2bYrdXrwhereYt(Xt)=Yr(Xr),Xt(a)=Xr(k1a),Xt(b)=Xr(k2b)
path signature
对于一条多维path X : [ a , b ] ↦ R d X:[a,b]\mapsto R^d X:[a,b]↦Rd, 首先我们给出其一阶path signature的表达式为:
S ( X ) a , t n = ∫ a t d X c n , t ∈ [ a , b ] S(X)_{a,t}^n=\int_a^tdX_c^n,\ t\in[a,b] S(X)a,tn=∫atdXcn, t∈[a,b]
它对应路径积分中 Y t = 1 , X t = X c n Y_t=1,X_t=X^n_c Yt=1,Xt=Xcn的情况,其中 X c n X_c^n Xcn表示路径 X X X的第 n n n个维度在 c c c时刻的取值。对于 d d d维的path,其一阶path signature有 d d d个,可以看出它们的物理意义就是时间间隔内相应维度值的变化量 Δ X n \Delta X^n ΔXn:
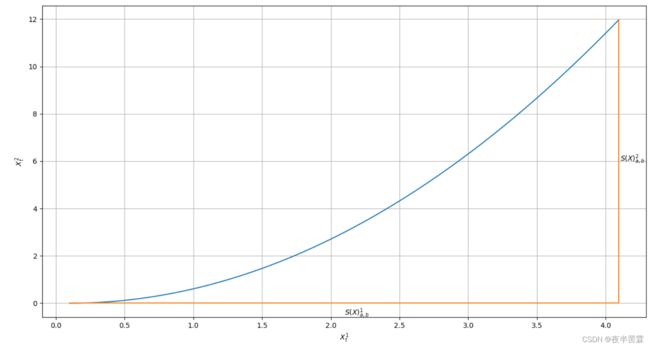
值得注意的是由于一阶path signature的积分上限是变化的 t t t,而非定值 b b b,所以实际上 S ( X ) a , t n S(X)^n_{a,t} S(X)a,tn是也是一个一维path X : [ a , b ] ↦ R , X t = { S ( X ) a , t n } X:[a,b]\mapsto R,X_t=\{S(X)^n_{a,t}\} X:[a,b]↦R,Xt={S(X)a,tn}吗,因此我们可以对它再次求取路径积分得到了二阶path signature:
S ( X ) a , t n , m = ∫ a t S ( X ) a , c n d X c m = ∫ a t ∫ a c d X s n d X c m \begin{aligned} S(X)^{n,m}_{a,t}&=\int_a^tS(X)^n_{a,c}dX_c^m\\ &=\int_a^t\int_a^cdX^n_sdX_c^m \end{aligned} S(X)a,tn,m=∫atS(X)a,cndXcm=∫at∫acdXsndXcm
二阶path signature是对一阶path signature求路径积分得到,随着一阶PS和积分变量的不同,共有 d 2 d^2 d2个二阶PS。现给出二维path的二阶PS特征表达式及物理意义:
S ( X ) a , t 1 , 1 = ∫ a t ∫ a c d X s 1 d X c 1 = ( X 1 b − X 1 a ) 2 2 ( 1 ) S ( X ) a , t 2 , 2 = ∫ a t ∫ a c d X s 2 d X c 2 = ( X 2 b − X 2 a ) 2 2 ( 2 ) S ( X ) a , t 1 , 2 = ∫ a t ∫ a c d X s 1 d X c 2 ( 3 ) S ( X ) a , t 2 , 1 = ∫ a t ∫ a c d X s 2 d X c 1 ( 4 ) S(X)^{1,1}_{a,t}=\int_a^t\int_a^cdX^1_sdX_c^1=\frac{(X^b_1-X^a_1)^2}{2}\ (1)\\ S(X)^{2,2}_{a,t}=\int_a^t\int_a^cdX^2_sdX_c^2=\frac{(X^b_2-X^a_2)^2}{2}\ (2)\\ S(X)^{1,2}_{a,t}=\int_a^t\int_a^cdX^1_sdX_c^2\ (3)\\ S(X)^{2,1}_{a,t}=\int_a^t\int_a^cdX^2_sdX_c^1\ (4) S(X)a,t1,1=∫at∫acdXs1dXc1=2(X1b−X1a)2 (1)S(X)a,t2,2=∫at∫acdXs2dXc2=2(X2b−X2a)2 (2)S(X)a,t1,2=∫at∫acdXs1dXc2 (3)S(X)a,t2,1=∫at∫acdXs2dXc1 (4)
式(1),(2)比较好理解,就是相应维度取值变化量的平方,式(3),(4)需要结合路径积分的重参数不变性来理解,即路径积分实际上讨论的是不同维度路径间的相对关系,而与参变量的具体取值无关,于是我们可以将式(3),(4)改写成如下形式:
S ( X ) a , t 1 , 2 = ∫ X a 2 X t 2 S ( X ) a , t 1 d X 2 = ∫ X a 2 X t 2 ( X c 1 − X 0 1 ) d X 2 S ( X ) a , t 2 , 1 = ∫ X a 1 X t 1 S ( X ) a , t 2 d X 1 = ∫ X a 1 X t 1 ( X c 2 − X 0 2 ) d X 1 S(X)^{1,2}_{a,t}=\int_{X^2_a}^{X^2_t}S(X)^1_{a,t}dX^2=\int_{X^2_a}^{X^2_t}(X_c^1-X_0^1)dX^2\\ S(X)^{2,1}_{a,t}=\int_{X^1_a}^{X^1_t}S(X)^2_{a,t}dX^1=\int_{X^1_a}^{X^1_t}(X_c^2-X_0^2)dX^1 S(X)a,t1,2=∫Xa2Xt2S(X)a,t1dX2=∫Xa2Xt2(Xc1−X01)dX2S(X)a,t2,1=∫Xa1Xt1S(X)a,t2dX1=∫Xa1Xt1(Xc2−X02)dX1
结合积分的意义,实际上它就是在计算高为 ( X c 1 − X 0 1 ) (X_c^1-X_0^1) (Xc1−X01),宽度为 d X 2 dX^2 dX2矩形元的面积累加,直观理解如下图:

后续阶次的PS均可通过对前一阶的PS再求路径积分得到,又我们通常假定0阶的PS为1,则一阶的PS也可认为是对0阶PS求取路径积分得到。至此,我们得到了PS为所有阶次特征的集合如下:
S ( X ) a , b = [ 1 , S ( X ) a , b 1 . . . S ( X ) a , b d , S ( X ) a , b 1 , 2 . . . S ( X ) a , b d − 1 , d . . . ] S(X)_{a,b}=[1,S(X)_{a,b}^1...S(X)_{a,b}^d,S(X)_{a,b}^{1,2}...S(X)_{a,b}^{d-1,d}...] S(X)a,b=[1,S(X)a,b1...S(X)a,bd,S(X)a,b1,2...S(X)a,bd−1,d...]
其上标遍历如下多重索引:
W = { ( i 1 , . . . , i k ) ∣ k ≥ 1 , i 1 , . . . i k ∈ { 1 , . . . , d } } W=\{(i_1,...,i_k)|k\geq1,i_1,...i_k\in\{1,...,d\}\} W={(i1,...,ik)∣k≥1,i1,...ik∈{1,...,d}}
除0外第 k k k阶的PS都由前一阶的PS再次求取路径积分得到。
path signature 性质
path signature拥有许多良好的性质,之前介绍过的平移不变性就是其中之一,即path的开始位置对于特征的求取没有影响,在图像处理方面这是一个十分良好的性质。
根据shuffle product identity定理[^3],PS的低阶项乘积可以通过高阶项的线性组合得到,这就意味更高阶次的PS特征是描述了path细粒度的特征,而且我们可以只使用高阶特征的线性组合来获取低层次的大尺寸特征。
path和PS特征几乎是一一对应的[^3]
path signature变体
path signature拥有平移不变性,但是没有尺度不变以及旋转不变的特性,因此有一些基于这些不变性方面的研究以给出改进的PS特征。
LNPS
Length Normalized Path Signature[^2]是具有尺度不变性的PS特征,即当path等比例放大时,特征保持不变。其计算方式也十分的简单:
首先我们要通过曲线积分计算path X X X的长度 L L L:
L = ∫ 1 d s L=\int1ds L=∫1ds
然后对 k k k阶的PS特征除以 L k L^k Lk以获得尺度归一化的PS特征:
S ( X ) ∣ L N = { 1 , I ( x ) L , I 2 ( x ) L 2 , . . . , I k ( x ) L k } S(X)|^{LN}=\{1,\frac{I(x)}{L},\frac{I^2(x)}{L^2},...,\frac{I^k(x)}{L^k}\} S(X)∣LN={1,LI(x),L2I2(x),...,LkIk(x)}
其中 I k ( x ) I^k(x) Ik(x)为 k k k阶的PS特征,之所以不同阶特征要除以不同系数来实现归一化是高阶次特征有更多的乘积分操作,其尺度与低阶特征不同,基本呈指数变化。
Rotation invariance PS
二维PS特征本身不具有旋转不变性,但是其偶阶次项经过一定的线性组合可以构成拥有旋转不变性的特征。给出这样的线性组合规律如下:
我们定义 ϕ \phi ϕ为复二维形式级数空间的一个取值,其中的每一个级数项我们都认为对应一个PS特征,,形如 x 1 + x 2 x 1 + 3 x 1 x 1 x 2 x_1+x_2x_1+3x_1x_1x_2 x1+x2x1+3x1x1x2对应 S ( x ) 1 + S ( X ) 1 , 2 + 3 S ( X ) 1 , 1 , 2 S(x)^1+S(X)^{1,2}+3S(X)^{1,1,2} S(x)1+S(X)1,2+3S(X)1,1,2。
充分条件
那么如果 ϕ \phi ϕ对应的PS特征线性组合具有旋转不变性,则 ϕ \phi ϕ应该满足
ϕ = c i 1 . . . i n c i 1 . . . i n = z i 1 ⋅ z i 2 ⋅ . . . z i n z 1 = x 1 + i x 2 z 2 = x 1 − i x 2 w h e r e n ≥ 2 a n d i 1 , . . . i 2 ∈ { 1 , 2 } b e s u c h t h a t # { k : i k = 1 } = # { k : i k = 2 } \begin{aligned} \phi&=c_{i_1...i_n}\\ c_{i_1...i_n}& =z_{i_1}\cdot z_{i_2}\cdot...z_{i_n}\\ z_1& =x_1+ix_2\\ z_2&=x_1-ix_2 \end{aligned}\\ where n\geq2 \ and\ i_1,...i_2\in\{1,2\} be\ such\ that \#\{k:i_k=1\}=\#\{k:i_k=2\} ϕci1...inz1z2=ci1...in=zi1⋅zi2⋅...zin=x1+ix2=x1−ix2wheren≥2 and i1,...i2∈{1,2}be such that#{k:ik=1}=#{k:ik=2}
其中 # { f } \#\{f\} #{f}用于统计满足条件f的元素个数,我们取 ϕ \phi ϕ的实部或者虚部作为满足旋转不变性的PS特征线性组合。
基底
我们记shuffle product 符号为 Ш Ш Ш,两个单项式的shuffle product为保证每个单项式内元素顺序不变情况下的排列组合乘积,如
x 1 x 2 Ш x 1 x 2 = x 1 x 2 x 1 x 2 + x 1 x 2 x 1 x 2 + x 1 x 1 x 2 x 2 + x 1 x 2 x 2 x 2 + x 1 x 2 x 1 x 2 + x 1 x 2 x 1 x 2 = 2 x 1 x 2 x 1 x 2 + 4 x 1 x 2 x 1 x 2 x_1x_2Шx_1x_2=x_1x_2x_1x_2+x_1x_2x_1x_2+x_1x_1x_2x_2+x_1x_2x_2x_2+x_1x_2x_1x_2+x_1x_2x_1x_2\\ =2x_1x_2x_1x_2+4x_1x_2x_1x_2 x1x2Шx1x2=x1x2x1x2+x1x2x1x2+x1x1x2x2+x1x2x2x2+x1x2x1x2+x1x2x1x2=2x1x2x1x2+4x1x2x1x2
而又有shuffle identity定理,我们可以知道对应于两个单项式的低阶PS特征等于这两个单项式的shuffle produtct对应的PS特征,因此我们可以通过计算低阶旋转不变特征的shuffle product来获得高阶的旋转不变PS特征,并依次计算出对应阶次的基底。
参考文献
[1]《A Primer on the Signature Method in Machine Learning》
[2]《Online Signature Verification using Recurrent Neural Network and Length-normalized Path Signature Descriptor》
[3]《Rotation invariants of two dimensional curves based on iterated integrals》
[4] path signature introduction