第一题 零钱兑换
题目
贪心(无效)
在日常的生活中 ,如果我们要进行零钱兑换,最朴素的思维自然是
如果可以使用更大面值的硬币,就优先选择它
这也正是贪心算法的思维
代码
func coinChange(coins []int, amount int) int {
var res int
sort.Ints(coins)
if amount==0{return 0}
for amount>=coins[0]{
index:=sort.SearchInts(coins,amount)
if index==len(coins){
amount-=coins[len(coins)-1]
res++
continue
}
if coins[index]!=amount {
amount-=coins[index-1]
}else{
amount-=coins[index]
}
res++
}
if amount!=0 {return -1}
return res
}但无法提交通过
原因是因为
题目提供的硬币组合不一定是日常中使用的硬币组合
大面值的硬币不一定是局部最优解
部分可以使用小面值组合组成的数字无法使用大面值表示
如果想要继续使用贪心算法,则需要加入回溯语句,排除使用大面值解的方案,再继续搜索
由于效率过低,在此不继续进行优化
后续优化思路可参考精选题解
https://leetcode-cn.com/probl...
动态规划
我们可以发现
寻找硬币组合的过程
本质上可以拆解成为一个一个挑选硬币的结果
例如:
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
动态规划的解题过程为实质为求解dp[11]的过程
在挑选第一个硬币时,有三种挑选的方案
挑选硬币1,硬币个数为dp[10]+1
挑选硬币2,硬币个数为dp[9]+1
挑选硬币5,硬币个数为dp[6]+1
在三个方案中选出个数最小的方案,即为dp[11]的解
因此可以得到
dp[amount]=min{dp[amount-coins[0],dp[amount-coins[1],...,dp[amount-coins[n-1]}+1
详细代码为
func coinChange(coins []int, amount int) int {
//初始化数组,由于硬币为整型,挑选的硬币组合个数最大不可能大于面值amount
max := amount + 1
dp :=make([]int,max)
for i:=range dp{
dp[i]=max
}
dp[0] = 0
for i := 1; i amount {
return -1
}else{
return dp[amount]
}
}
func min(x int,y int)int{
if x 复杂度分析
时间复杂度:O(Sn),其中 S 是金额amount,n 是面额数len(coins)。我们一共需要计算 O(S) 个状态,S 为题目所给的总金额。对于每个状态,每次需要枚举 n 个面额来转移状态,所以一共需要 O(Sn) 的时间复杂度。
空间复杂度:O(S)。数组 dp 需要长度为总金额 S 的空间。
第二题 最长上升子序列
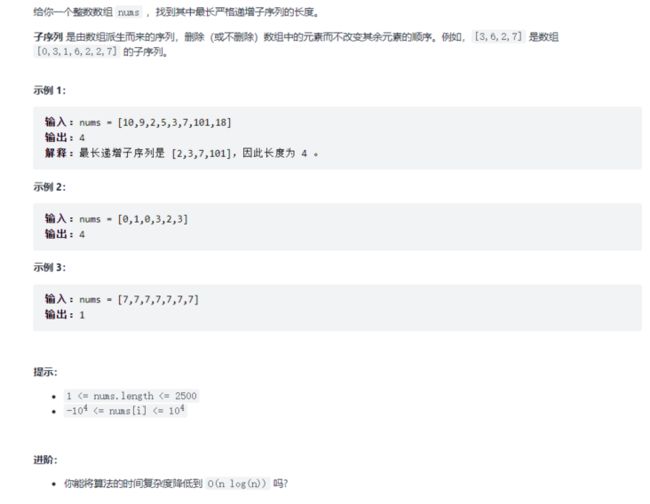
题目
思路
子序列的搜索过程显然具有最有子结构性质
对于i长度的序列
可以计算出以第一个元素为开始的前i-1个子序列的最优解
dp[i]的解即为所有满足递增的局部最优解中最长的一个加一
代码
func lengthOfLIS(nums []int) int {
if len(nums) == 0 {
return 0
}
dp := make([]int, len(nums))
dp[0] = 1
maxans := 1
for i := 1; i < len(nums); i++ {
dp[i] = 1
for j := 0; j < i; j++ {
if nums[i] > nums[j] {
dp[i] = max(dp[i], dp[j]+1)
}
}
maxans = max(maxans, dp[i])
}
return maxans
}
func max(x int,y int)int{
if x>y{
return x
}else{
return y
}
}复杂度分析
时间复杂度:O(n^2),其中 n 为数组 nums 的长度。动态规划的状态数为 n,计算状态 dp[i] 时,需要 O(n) 的时间遍历 dp[0…i−1] 的所有状态,所以总时间复杂度为 O(n^2)
空间复杂度:O(n),需要额外使用长度为 n 的 dp 数组。
优化-贪心+二分
参考官解
https://leetcode-cn.com/probl...
思路与算法
考虑一个简单的贪心,如果我们要使上升子序列尽可能的长,则我们需要让序列上升得尽可能慢,因此我们希望每次在上升子序列最后加上的那个数尽可能的小。
基于上面的贪心思路,我们维护一个数组 d[i] ,表示长度为 i 的最长上升子序列的末尾元素的最小值,用 l 记录目前最长上升子序列的长度,起始时 l 为 1,d[1]=nums[0]。
同时我们可以注意到 d[i] 是关于 i 单调递增的。因为如果d[j]≥d[i] 且 j 我们依次遍历数组 nums 中的每个元素,并更新数组 d 和 l 的值。如果 nums[i]>d[len] 则更新 len=len+1,否则在 d[1…len]中找满足 d[i−1] 根据 d 数组的单调性,我们可以使用二分查找寻找下标 i,优化时间复杂度。 最后整个算法流程为: 设当前已求出的最长上升子序列的长度为 len(初始时为 1),从前往后遍历数组 nums,在遍历到 nums[i] 时: 如果 nums[i]>d[len] ,则直接加入到 d 数组末尾,并更新 len=len+1; 否则,在 d 数组中二分查找,找到第一个比 nums[i] 小的数 d[k] ,并更新d[k+1]=nums[i]。 以输入序列 [0, 8, 4, 12, 2] 为例: 第一步插入 0,d = [0]; 第二步插入 8,d = [0, 8] 第三步插入 4,d = [0, 4] 第四步插入 12,d = [0, 4, 12] 第五步插入 2,d = [0, 2, 12] 最终得到最大递增子序列长度为 3。 代码 复杂度分析 时间复杂度:O(nlogn)。数组 nums 的长度为 n,我们依次用数组中的元素去更新 d 数组,而更新 d 数组时需要进行 O(logn) 的二分搜索,所以总时间复杂度为 O(nlogn)。 空间复杂度:O(n),需要额外使用长度为 n 的 d 数组。func lengthOfLIS(nums []int) int {
l := 1
n := len(nums)
if n == 0 {
return 0
}
d:=make([]int,n+1)
d[l] = nums[0]
for i := 1; i < n; i++ {
if nums[i] > d[l] {
l++
d[l] = nums[i]
} else {
ll := 1
rr := l
pos := 0 // 如果找不到说明所有的数都比 nums[i] 大,此时要更新 d[1],所以这里将 pos 设为 0
for ll <= rr {
mid := (ll + rr) >> 1
if d[mid] < nums[i] {
pos = mid
ll = mid + 1
} else {
rr = mid - 1
}
}
d[pos + 1] = nums[i]
}
}
return l
}