算法--排序

算法基础系列

---

前言

 在算法题中，常见的是排序是 快速排序(快排) 和 归并排序(重点)，因此只介绍以上两种算法的模板以及相应练习题

各类排序算法

---

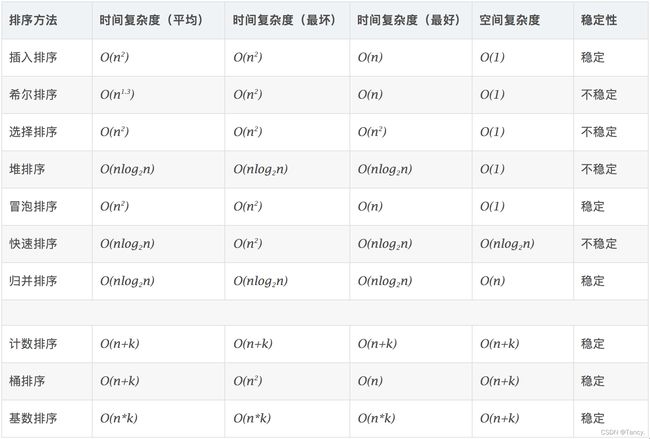
各类排序算法的时间复杂度

---

快速排序

概念

属于 交换排序 一类

是分治算法
分治算法有三步

1. 分成子问题
2. 递归处理子问题
3. 子问题合并

基本思想：通过一趟排序，将待排序记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录进行排序，以达到整个序列有序

个人理解：双指针方法，找一个数x把数组分为两半(随机值，一般是中间数)，在左边找一个大于x的数，右边找一个小于x的数，两者交换位置，直到两个指针相遇，详见代码注释版

模板

注释版

void quick_sort(int q[], int l, int r)
{
    //递归的终止情况
    if(l >= r) return;
    //第一步：分成子问题
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while(i < j)
    {
        do i++; while(q[i] < x);//在x 的左边找到第一个大于x 的数
        do j--; while(q[j] > x);//在x 的右边找到第一个小于x 的数
        if(i < j) swap(q[i], q[j]);//两个指针未相遇  交换
    }
    //第二步：递归处理子问题
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
    //第三步：子问题合并.快排这一步不需要操作，但归并排序的核心在这一步骤
}

纯净版

void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

---

归并排序

概念

归并排序本质上还是属于分治的思想，要递归

归并和二分的区别

• 二分是随机数为分界点，先排序再递归
• 归并是中间数为分界点，先递归左右两边再合并排序

归并的核心是：一分为二，合二为一(重点)

难点在合二为一
思想是双指针方法，分别指向a,b的第一个数开始比较，若a数组中的数小于b数组，则a数组中的该位置的数加入总数组中，指针向后移动一位。
当一个数组a已经指向最后一位而另一个数组b未指向最后一位时，不必在做比较，b数组当前位置以后的数都大于a中的所有数

模板

注释版

void merge_sort(int q[], int l, int r)
{
    //递归的终止情况
    if(l >= r) return;
    //第一步：分成子问题
    int mid = l + r >> 1;//一分为二
    //第二步：递归处理子问题
    merge_sort(q, l, mid ), merge_sort(q, mid + 1, r);
    //第三步：合并子问题
    int k = 0, i = l, j = mid + 1, tmp[r - l + 1];
    while(i <= mid && j <= r)//两个子数组比较
        if(q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    while(i <= mid) tmp[k++] = q[i++];
    while(j <= r) tmp[k++] = q[j++];

    for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k];
}

纯净版

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

---

练习题

快速排序

快速排序

模板题

#include 

using namespace std;

const int N = 1e5 + 10;

int n, a[N];

void quick_sort(int q[], int l, int r)
{
    if (l >= r)
        return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do
            i++;
        while (q[i] < x);
        do
            j--;
        while (q[j] > x);
        if (i < j)
            swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> a[i];
    quick_sort(a, 0, n - 1);
    for (int i = 0; i < n; i++)
        cout << a[i] << " ";
    return 0;
}

第k个数

第k个数

在上一题的基础上加几句话即可

#include 

using namespace std;

const int N = 1e5 + 10;

int n, k, a[N];

void quick_sort(int q[], int l, int r)
{
    if (l >= r)
        return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do
            i++;
        while (q[i] < x);
        do
            j--;
        while (q[j] > x);
        if (i < j)
            swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

int main()
{
    cin >> n >> k;
    for (int i = 0; i < n; i++)
        cin >> a[i];
    quick_sort(a, 0, n - 1);
    for (int i = 0; i < n; i++)
        if (i==k-1)
            cout << a[i] << " ";
    return 0;
}

归并排序

归并排序

模板题

#include 

using namespace std;

const int N = 100010;

int n, a[N], tmp[N];

void merge_sort(int q[], int l, int r)
{
    if (l == r)
        return;
    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r) //直到某一个数组比完
        if (q[i] <= q[j])
            tmp[k++] = q[i++];
        else
            tmp[k++] = q[j++];

    //如果有剩余
    while (i <= mid)
        tmp[k++] = q[i++];

    while (j <= r)
        tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i++, j++)
        q[i] = tmp[j];
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> a[i];

    merge_sort(a, 0, n - 1);

    for (int i = 0; i < n; i++)
        cout << a[i] << " ";

    return 0;
}

逆序对的数量

逆序对的数量

求解逆序对问题,实际上有三种算法可以处理,分别是冒泡算法,归并排序,以及树状数组求解.

这里显然我们可以用性价比最高,代码最好写,效率特高的归并排序算法.

我们要注意一点,就是当我们发现填充第二个数组中的数,加入备用数组的使用,都要统计 $mid-i+1$ ,因为此时此刻,我们第一个数组中剩余的所有数,都会和它构成逆序对.

#include 

using namespace std;

const int N = 100010;

typedef long long LL;

int n, a[N], tmp[N];

LL merge_sort(int q[], int l, int r)
{
    if (l >= r)
        return 0;
    int mid = l + r >> 1;

    LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;

    while (i <= mid && j <= r) //直到某一个数组比完
        if (q[i] <= q[j])
            tmp[k++] = q[i++];
        else
        {
            tmp[k++] = q[j++];
            res += mid - i + 1;
        }

    //如果有剩余
    while (i <= mid)
        tmp[k++] = q[i++];

    while (j <= r)
        tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i++, j++)
        q[i] = tmp[j];

    return res;
}

int main()
{

    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", &a[i]);

    cout << merge_sort(a, 0, n - 1) << endl;

    return 0;
}