一些经典的递归题

写递归题一定要考虑两个要素：递归终止条件和迭代条件

汉诺塔问题

问题描述

现在有三个柱子，编号A,B,C.现在有n个圆盘，规定圆盘只能把小圆盘放在大圆盘上（不能大圆盘放在小圆盘上），初始n个圆盘全部在A柱上，现在要把A的圆盘全部移动在C上

请你返回你的移动步骤，使得移动次数最少

思路求解

这道题我们可能一时之间难以实现，我们可以把子问题给进行分解

试想：我们如果要把2个圆盘挪动需要什么步骤？

• 把上面一个移动到中间
• 把最后一个移动到目标处
• 把中间的圆盘移动到目标处

既然这样，我们可以进行一下推广：

如果我们有n个圆盘的话：

• 把上面n-1个圆盘移动到中间
• 把最后一个圆盘移动到目标处
• 把中间的n-1个圆盘移动到目标处

就像这样：

然后对于上面n-1的圆盘，我们可以考虑从n-2到n-1重复调用此过程

这就是我们的最优解法了

所以我们的初始函数可能需要以下过程

if(n==1)
{
	A->C;//只有一个圆盘的情况
}

fromAToB(n-1);//把上面n-1个圆盘放在中间的函数
A->C;//把当前圆盘堆最后一个圆盘放在目标处
fromBToC(n-1);//把中间的圆盘全部放在目标处
}

对于过程中的两个函数，大家可以暂时把它们想成黑盒子，它们只执行了移动过程

因为我们的主过程是从A到C，所以我们的主函数是fromAToC(n)

至于我们中间涉及到的函数，我们可以仿照我们的思想，轻松给它补上

例如fromAtoB

if(n==1)
{
	A->B;//只有一个圆盘的情况
}

fromAToC(n-1);//把上面n-1个圆盘先存放在C
A->B;//把当前圆盘堆最后一个圆盘放在目标处
fromCToB(n-1);//把中间的圆盘放回目标处

依次类推，我们写出了六个函数相互依赖的解法

	void hanoiTest2(int n)
	{
		fromAToC(n);//我们的主过程

	}
	void fromAToB(int n)
	{
		if (n == 1)
		{
			cout << "1号：" << "A->B" << endl;
			return;
		}
		fromAToC(n - 1);
		cout << n << "号：" << "A->B" << endl;
		fromCToB(n - 1);
	}

	void fromAToC(int n)
	{
		if (n == 1)
		{
			cout << "1号：" << "A->C" << endl;
			return;
		}
		fromAToB(n - 1);
		cout << n << "号：" << "A->C" << endl;
		fromBToC(n - 1);
	}

	void fromBToC(int n)
	{
		if (n == 1)
		{
			cout << "1号：" << "B->C" << endl;
			return;
		}
		fromBToA(n - 1);
		cout << n << "号：" << "B->C" << endl;
		fromAToC(n - 1);
	}

	void fromBToA(int n)
	{
		if (n == 1)
		{
			cout << "1号：" << "B->A" << endl;
			return;
		}
		fromBToC(n - 1);
		cout << n << "号：" << "B->A" << endl;
		fromCToA(n - 1);
	}

	void fromCToA(int n)
	{
		if (n == 1)
		{
			cout << "1号：" << "C->A" << endl;
			return;
		}
		fromCToB(n - 1);
		cout << n << "号：" << "C->A" << endl;
		fromBToA(n - 1);
	}

	void fromCToB(int n)
	{
		if (n == 1)
		{
			cout << "1号：" << "C->B" << endl;
			return;
		}
		fromCToA(n - 1);
		cout << n << "号：" << "C->B" << endl;
		fromAToB(n - 1);
	}

我们如何把上面这个函数改成递归版本呢？

设我们的三个柱子分别为from,other,to
其中from代表圆盘刚开始的位置，to代表我们移动的目标位置，other代表另外的辅助位置

我们的目标是把from的所有圆盘移动到to

我们把上面函数这三个过程改一下即可

fromAToC(n-1);//把上面n-1个圆盘先存放在C
A->B;//把当前圆盘堆最后一个圆盘放在目标处
fromCToB(n-1);//把中间的圆盘放回目标处

第一个过程，我们是先把上面的n-1个圆盘移动到辅助位置，方便我们最大的圆盘进行移动
所以我们的第一个过程针对上面n-1个圆盘，目标改成了other，利用to把它们移动到other

第二个过程，我们把最大的圆盘从from移动到to

第三个过程，我们需要归位，即把中间的圆盘从other移动到to，辅助位置是from

我们对于上面n-1个位置，重复此过程，即可把大问题分解

	void hanoiTest1(int n,string from, string to, string other)
	{
		if (n == 1)
		{
			cout << n<<"号盘子:"<<from << "->" << to <<endl;
			return;
		}

		hanoiTest1(n - 1, from, other, to);//第一步，n-1从from到other
		cout << n << "号盘子:" << from << "->" << to <<endl;//第二步，n自己从from到to

		hanoiTest1(n - 1, other, to, from);//第三步，n-1从other到to
	}

下来把我们的两个问题测试一下

大家可以通过这个网站来测试我们答案的正确性http://www.7k7k.com/swf/201271.htm

子字符串问题

问题描述：

给你一个任意的字符串，输出它所有的子序列

例如：“abc”

输出：“a”,“b”,“c”,“ab”,“ac”,“bc”,“abc”

思路求解：

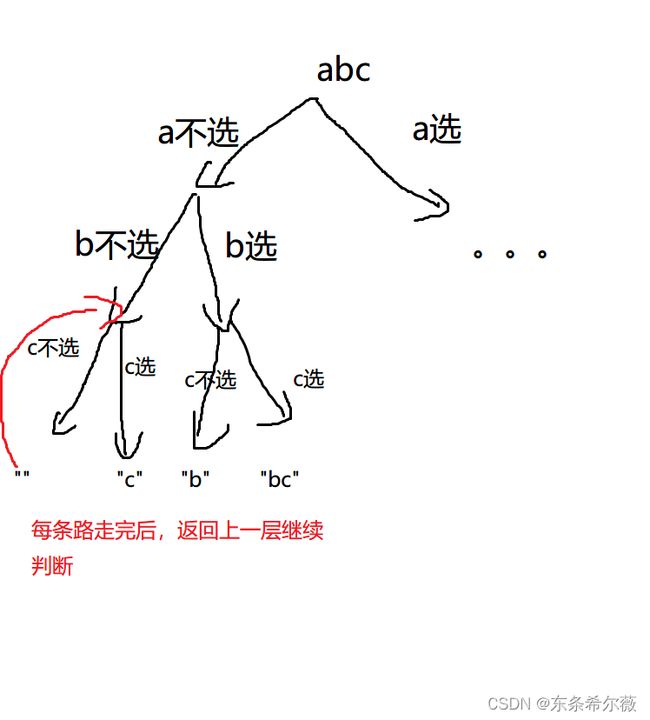
我们这道题，其实无非就可以分解成两个情况某个字符选，还是不选

我们可以遍历每个字符串，分为它们选了，或者没选这两种情况来判断，直到所有字符判断完毕，再进行回溯判断

就像这样：

所有我们需要以下的参数

返回值数组vector,我们使用递归时，如果需要记录答案，最好将其作为引用参数

下标index,判断字符串中字符是否判断完毕

字符串path,记录当前的选择方法

以及我们的原数组

代码如下，详细可见注释

	vector<string>PrintAllSubsquences(string s)
	{
		int index = 0;
		string path = "";
		vector<string>ans;
		_PrintAllSubsquences(s, index, path, ans);
		return ans;
	}
	void _PrintAllSubsquences(string s, int index, string path, vector<string>&ans)
	{
		if (index == s.size())//字符串被判断完了
		{
			ans.push_back(path);
			return;
		}

		_PrintAllSubsquences(s, index + 1, path, ans);//当前字符不选的情况，继续往下判断
		_PrintAllSubsquences(s, index + 1, path+s[index], ans);//当前字符选的情况，继续往下递归
	}

上面这个代码我们可能遇到重复子串的问题，例如我们需要求"accc"的子串

有大量的重复

为了避免这个问题，我们在接受答案的时候最好使用哈希集合（unordered_set）这个容器

字符串全排列

问题描述：

给你一个字符串，求出字符串的所有排列

例如：“abc”

输出：“abc”,“acb”,“bac”,“bca”,“cab”,“cba”

思路求解：

我们可以根据原字符串，进行交换即可

例如：我们的0位置与0位置交换，代表我们本次字符不交换

我们0和1位置交换，就形成了"bac"这个字符串

我们可以遍历每个字符，再把它与每个字符尝试进行交换

所以我们可以写出以下代码

	void _PrintAllPermutations(string s, int index, vector<string>& ans)
	{
		if (index == s.size())
		{
			ans.push_back(s);//字符遍历完了，将交换所得的字符串返回
			return;
		}
		for (int i = index; i < s.size(); i++)
		{
			Swap(s, index, i);
			_PrintAllPermutations(s, index + 1, ans);//遍历下一个位置的所有交换选择
			
		}
	}

不过这个代码是错误的

我们在递归回溯的过程中，通常需要恢复现场

因为我们在这一层进行交换了后，回溯到上一层函数的话，就是拿交换后的字符串进行排序了，答案最终就不正确

所以我们要在每次递归完成后，恢复现场

	void _PrintAllPermutations(string s, int index, vector<string>& ans)
	{
		if (index == s.size())
		{
			ans.push_back(s);//字符遍历完了，将交换所得的字符串返回
			return;
		}
		for (int i = index; i < s.size(); i++)
		{
			Swap(s, index, i);
			_PrintAllPermutations(s, index + 1, ans);//遍历下一个位置的所有交换选择
			Swap(s, index, i);//恢复现场
		}
	}

我们这个代码还可以进行一个去重优化

设置一个bool used[128]的数组，记录操作的字符如果某个字符没有出现，才进行操作

完整代码如下

	vector<string>PrintAllPermutations(string s)
	{
		int index = 0;
		vector<string>ans;
		_PrintAllPermutations(s, index, ans);
		return ans;
	}
	void _PrintAllPermutations(string s, int index, vector<string>& ans)
	{
		if (index == s.size())
		{
			ans.push_back(s);
			return;
		}

		bool isUsed[128] = { 0 };
		for (int i = index; i < s.size(); i++)
		{

			if (!isUsed[(int)s[i]])
			{
				isUsed[(int)s[i]] = true;
				Swap(s, index, i);
				_PrintAllPermutations(s, index + 1, ans);
				Swap(s, index, i);
			}
		}
	}

	void Swap(string& s, int x, int y)
	{
		char tmp = s[x];
		s[x] = s[y];
		s[y] = tmp;
	}

逆序栈

问题描述：

给你一个栈，要求只能使用递归，并且不能开辟额外的数据结构，将此栈进行逆序操作

思路求解：

我们如果想要逆序栈，首先要想办法拿到栈底元素，并且还需要将栈底上面的元素按照原顺序重新压入

例如我们有这个栈

我们需要一个函数，在不影响2,3顺序的情况，拿出1

我们可以这样：

先拿出一个元素，再判断是否为空

为空直接返回当前栈就一个元素，顶部当然是它本身

然后我们这样递归函数堆栈底层不断把答案往上返回

所以我们递归取得栈底的代码如下

	int f(stack<int>& s)
	{
		int result = s.top();//拿到当前顶部
		s.pop();
		if (s.empty())
		{
			return result;
		}
		else
		{
			int last = f(s);//不断往下，可拿到底部
			s.push(result);//当前函数栈帧记录了值，可直接放下
			return last;//将底部不断往上返回
		}

	}

我们的主函数中，就需要不断拿出栈底，在每层栈帧中记录拿到的值，再依次进行返回

	void reverseStack(stack<int>& s)
	{
		if (s.empty())
		{
			return;
		}

		int i = f(s);//将最后一位拿出来，并把上面元素按原序列重新放
		reverseStack(s);
		s.push(i);
	}