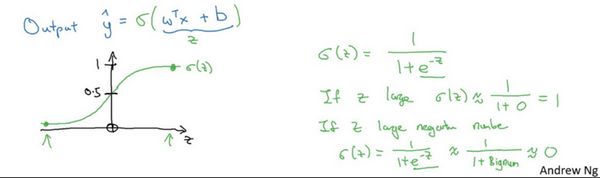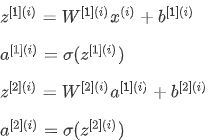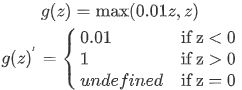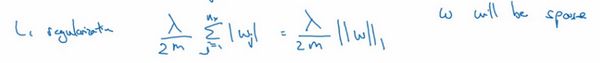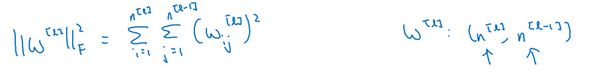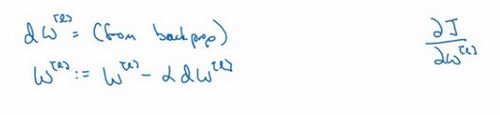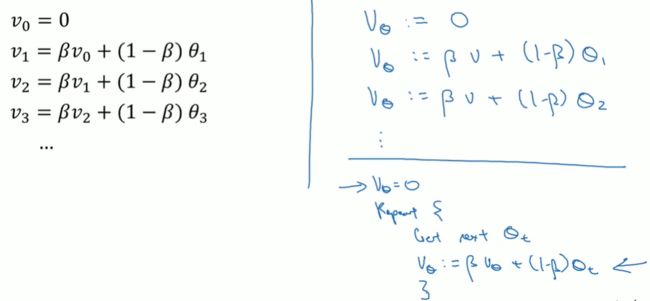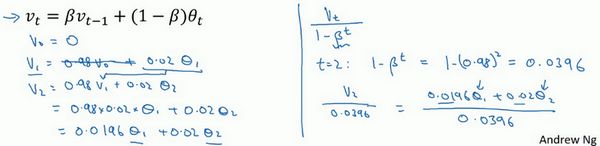吴恩达深度学习系列笔记
文章目录
- 深度学习概论
-
- 利用神经网络进行监督学习
-
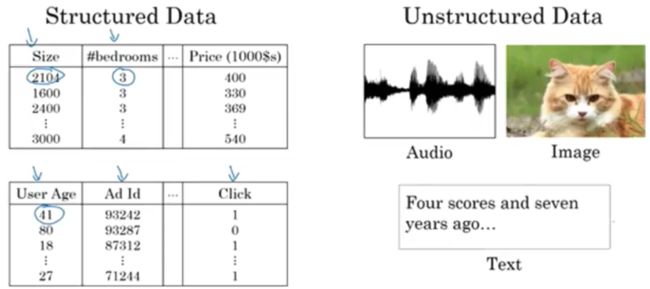
- 结构化数据、非结构化数据
- 神经网络基础
-
- 二分类
- Logistic 回归
- 逻辑回归的代价函数
-
- 为什么需要代价函数
- 损失函数
- 梯度下降法
- 计算图
- 逻辑回归中的梯度下降
- m个样本的梯度下降
- 向量化
-
- np.dot()
- 构建神经网络的基本步骤
- 浅层神经网络
-
- 神经网络的表示
- 计算一个神经网络的输出
-
- 神经网络的计算
- 多样本向量化
- 激活函数
- 为什么需要非线性激活函数
- 激活函数的导数
- 神经网络的梯度下降(Gradient descent for neural networks)
- 随机初始化
- 应用
- 深层神经网络(Deep Neural Network)
-
- 深层神经网络
- 前向传播和反向传播
- 深层网络中的前向传播
- 深层网络中的反向传播
- 核对矩阵的维数
- 为什么使用深层表示
- 搭建神经网络快
- 参数 VS 超参数
- 应用
- 深度学习的实用层面
-
- 训练、验证、测试集(Train/ Dev / Test sets)
- 偏差,方差(Bias / Variance)
- 机器学习基础
- 正则化
- 为什么正则化有利于预防过拟合呢?
- dropout正则化(Dropout Regularization)
-
- 在训练阶段如何实施**dropout**?
-
- **inverted dropout**(反向随机失活)
- 如何在测试阶段训练算法
- 理解dropout
- 其他正则化方法
-
- 数据扩增
- **early stopping**
- 归一化输入
-
- 为什么要归一化输入?
- 梯度消失/梯度爆炸
- 神经网络的权重初始化
- 梯度的数值逼近
- 梯度检验
- 梯度检验应用的注意事项
- 例题
- 优化算法
-
- Mini-batch 梯度下降
- 理解mini-batch梯度下降法
- 指数加权平均数
- 理解指数加权平均数
- 指数加权平均的偏差修正
- 动量梯度下降法
- RMSprop
- Adam优化算法
- 学习率衰减
- 局部最优的问题
- python实现
- 超参数调试、Batch正则化和程序框架
-
- 调试处理
- 为超参数选择合适的范围
- 超参数调试的实验:Pandas VS Caviar
- 归一化网络的激活函数
- 将Batch Norm拟合进神经网络
- Batch-norm为什么奏效?
- 测试时的Batch Norm
- Softmax回归
- 训练一个Softmax分类器
- 深度学习框架
- TensorFlow
- 例题
- 机器学习(ML)策略(1)
-
- 为什么是ML策略
- 正交化
- 单一数字评估指标
- 满足和优化指标
- 训练/开发/测试集划分
- 开发集和测试集的大小
- 什么时候该改变开发/测试集和指标
- 为什么是人的表现?
- 可避免偏差
- 理解人的表现
- 超过人的表现
- 改善你的模型的表现
- 例题
- 机器学习(ML)策略(2)
-
- 进行误差分析
- 清楚标注错误的数据
- 快速搭建你的第一个系统,并进行迭代
- 使用来自不同分布的数据,进行训练和测试
- 数据分布不匹配时,偏差与方差的分析
- 处理数据不匹配问题
- 迁移学习(Transfer Learning)
- 多任务学习
- 什么是端到端的深度学习?
- 是否要使用端到端的深度学习?
- 例题
- 卷积神经网络
-
- 是否要使用端到端的深度学习?
- 例题
深度学习概论
利用神经网络进行监督学习
图像数据可以使用CNN(s)
序列数据(音频,语言等)可以使用RNN(可以训练成一个有监督的学习问题)、LSTM
结构化数据、非结构化数据
神经网络基础
二分类
符号定义 :
x x x :
表示一个 n x n_{x} nx维数据,为输入数据,维度为 ( n x n_{x} nx,1);
y y y:
表示输出结果,取值为 ( 0 , 1 )
( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)):
表示第 i i i组数据,可能是训练数据,也可能是测试数据,此处默认为训练数据;
X = [ x ( 1 ) , x ( 2 ) , . . , x ( m ) ] X=[x^{(1)},x^{(2)},..,x^{(m)}] X=[x(1),x(2),..,x(m)]:
表示所有的训练数据集的输入值,放在一个 n x n_{x} nx∗m 的矩阵中,其中 m表示样本数目;
Y = [ y ( 1 ) , y ( 2 ) , . . , y ( m ) ] Y=[y^{(1)},y^{(2)},..,y^{(m)}] Y=[y(1),y(2),..,y(m)]:
对应表示所有训练数据集的输出值,维度为 1 ∗ m
Logistic 回归
下图是sigmoid函数的图像,如果我把水平轴作为 z z z轴,那么关于z的sigmoid函数是这样的,它是平滑地从0、走向1,让我在这里标记纵轴,这是0,曲线与纵轴相交的截距是0.5,这就是关于z的sigmoid函数的图像。我们通常都使用 z z z来表示 w T x + b w^{T}x+b wTx+b的值
关于sigmoid函数的公式是这样的, σ ( z ) = 1 1 + e − z \sigma(z)=\frac{1}{1+e^{-z}} σ(z)=1+e−z1,在这里 z z z是一个实数,这里要说明一些要注意的事情,如果 z z z非常大那么 e − z e^{-z} e−z将会接近于0,关于 z z z的sigmoid函数将会近似等于1除以1加上某个非常接近于0的项,因为 e e e的指数如果是个绝对值很大的负数的话,这项将会接近于0,所以如果很大的话那么关于的sigmoid函数会非常接近1。相反地,如果 z z z非常小或者说是一个绝对值很大的负数,那么关于这项 e − z e^{-z} e−z会变成一个很大的数,你可以认为这是1除以1加上一个非常非常大的数,所以这个就接近于0。实际上你看到当 z z z变成一个绝对值很大的负数,关于 z z z的sigmoid函数就会非常接近于0,因此当你实现逻辑回归时,你的工作就是去让机器学习参数 w w w以及 b b b这样才使得 y ^ \widehat{y} y 成为对 y = 1 y=1 y=1这一情况的概率的一个很好的估计
在继续进行下一步之前,介绍一种符号惯例,可以让参数 w w w和参数 b b b分开。在符号上要注意的一点是当我们对神经网络进行编程时经常会让参数 w w w和参数 b b b分开,在这里参数 b b b对应的是一种偏置。在之前的机器学习课程里,你可能已经见过处理这个问题时的其他符号表示。比如在某些例子里,你定义一个额外的特征称之为 x 0 x_{0} x0,并且使它等于1,那么现在 X X X就是一个 n x n_{x} nx加1维的变量,然后你定义的 y ^ = σ ( θ T x ) \widehat{y}=\sigma(\theta^{T}x) y =σ(θTx)的sigmoid函数。在这个备选的符号惯例里,你有一个参数向量 θ 0 , θ 1 , θ 2 , . . . , θ n \theta_{0},\theta_{1},\theta_{2},...,\theta{n} θ0,θ1,θ2,...,θn,这样 θ 0 \theta_{0} θ0就充当了 b b b,这是一个实数,而剩下的 θ 1 , θ 2 , . . . , θ n \theta_{1},\theta_{2},...,\theta{n} θ1,θ2,...,θn充当了 w w w,结果就是当你实现你的神经网络时,有一个比较简单的方法是保持 b b b和 w w w分开。但是在这节课里我们不会使用任何这类符号惯例,所以不用去担心。 现在你已经知道逻辑回归模型是什么样子了,下一步要做的是训练参数 b b b和参数 w w w,你需要定义一个代价函数,让我们在下节课里对其进行解释
逻辑回归的代价函数
为什么需要代价函数
为了训练逻辑回归模型的参数参数 w w w和参数 b b b我们,需要一个代价函数,通过训练代价函数来得到参数 w w w和参数 b b b。先看一下逻辑回归的输出函数:
为了让模型通过学习调整参数,你需要给予一个 m m m样本的训练集,这会让你在训练集上找到参数w和参数b,来得到你的输出
损失函数
损失函数又叫做误差函数,用来衡量算法的运行情况,Loss function: L ( y ^ , y ) L(\widehat{y},y) L(y ,y)
我们通过这个称为 L L L的损失函数,来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半,但是通常在逻辑回归中我们不这么做,因为当我们在学习逻辑回归参数的时候,会发现我们的优化目标不是凸优化,只能找到多个局部最优值,梯度下降法很可能找不到全局最优值,虽然平方差是一个不错的损失函数,但是我们在逻辑回归模型中会定义另外一个损失函数
我们在逻辑回归中用到的损失函数是:
L ( y ^ , y ) = − y log ( y ^ ) − ( 1 − y ) log ( 1 − y ^ ) L(\widehat{y},y)=-y\log(\widehat{y})-(1-y)\log(1-\widehat{y}) L(y ,y)=−ylog(y )−(1−y)log(1−y )
损失函数是在单个训练样本中定义的,它衡量的是算法在单个训练样本中表现如何
了衡量算法在全部训练样本上的表现如何,我们需要定义一个算法的代价函数,算法的代价函数是对 m m m个样本的损失函数求和然后除以 m m m:
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = 1 m ∑ i = 1 m ( − y ( i ) log y ^ ( i ) − ( 1 − y ^ ( i ) ) ) J(w,b)=\frac{1}{m}\sum^{m}_{i=1}L(\widehat{y}^{(i)},y^{(i)})=\frac{1}{m}\sum^{m}_{i=1}(-y^{(i)}\log\widehat{y}^{(i)}-(1-\widehat{y}^{(i)})) J(w,b)=m1∑i=1mL(y (i),y(i))=m1∑i=1m(−y(i)logy (i)−(1−y (i)))
损失函数只适用于像这样的单个训练样本,而代价函数是参数的总代价,所以在训练逻辑回归模型时候,我们需要找到合适的 w w w和 b b b,来让代价函数 J J J的总代价降到最低
梯度下降法
逻辑回归的代价函数(成本函数) J ( w , b ) J(w,b) J(w,b)是含有两个参数的
∂ \partial ∂表示求偏导符号,可以读作round, ∂ J ( w , b ) ∂ w \frac{{\partial}J(w,b)}{{\partial}w} ∂w∂J(w,b)就是对 w w w求偏导,在代码中我们会使用 d w dw dw表示这个结果;对应对 b b b求偏导就是 d b db db
计算图
可以说,一个神经网络的计算,都是按照前向或反向传播过程组织的。首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。
逻辑回归中的梯度下降
m个样本的梯度下降
当你应用深度学习算法,你会发现在代码中显式地使用for循环使你的算法很低效,同时在深度学习领域会有越来越大的数据集。所以能够应用你的算法且没有显式的for循环会是重要的,并且会帮助你适用于更大的数据集。所以这里有一些叫做向量化技术,它可以允许你的代码摆脱这些显式的for循环。
向量化
向量化是非常基础的去除代码中for循环的艺术,在深度学习安全领域、深度学习实践中,你会经常发现自己训练大数据集,因为深度学习算法处理大数据集效果很棒,所以你的代码运行速度非常重要,否则如果在大数据集上,你的代码可能花费很长时间去运行,你将要等待非常长的时间去得到结果。所以在深度学习领域,运行向量化是一个关键的技巧,让我们举个栗子说明什么是向量化。
在逻辑回归中你需要去计算 z = w T x + b z=w^{T}x+b z=wTx+b, w w w、 x x x都是列向量。如果你有很多的特征那么就会有一个非常大的向量,所以 w ∈ R n x w{\in}R^{n_{x}} w∈Rnx, x ∈ R n x x{\in}R^{n_{x}} x∈Rnx,所以如果你想使用非向量化方法去计算 w T x w^{T}x wTx,你需要用如下方式(python)
x
z=0
for i in range(n_x)
z+=w[i]*x[i]
z+=b
这是一个非向量化的实现,你会发现这真的很慢,作为一个对比,向量化实现将会非常直接计算 w T x w^{T}x wTx,代码如下:
z=np.dot(w,x)+b
这是向量化计算的方法,你将会发现这个非常快
np.dot()
np.dot(a,b)
#如果ab为向量,则它返回的是向量的内积
#如果ab为数组矩阵,则返回的是矩阵乘法
构建神经网络的基本步骤
-
定义模型结构(例如输入特征的数量)
-
初始化模型的参数
-
循环:
3.1 计算当前损失(正向传播)
3.2 计算当前梯度(反向传播)
3.3 更新参数(梯度下降)
def initialize_with_zeros(dim):
"""
此函数为w创建一个维度为(dim,1)的0向量,并将b初始化为0。
参数:
dim - 我们想要的w矢量的大小(或者这种情况下的参数数量)
返回:
w - 维度为(dim,1)的初始化向量。
b - 初始化的标量(对应于偏差)
"""
w = np.zeros(shape = (dim,1))
b = 0
#使用断言来确保我要的数据是正确的
assert(w.shape == (dim, 1)) #w的维度是(dim,1)
assert(isinstance(b, float) or isinstance(b, int)) #b的类型是float或者是int
return (w , b)
def propagate(w, b, X, Y):
"""
实现前向和后向传播的成本函数及其梯度。
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 矩阵类型为(num_px * num_px * 3,训练数量)
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据数量)
返回:
cost- 逻辑回归的负对数似然成本
dw - 相对于w的损失梯度,因此与w相同的形状
db - 相对于b的损失梯度,因此与b的形状相同
"""
m = X.shape[1]
#正向传播
A = sigmoid(np.dot(w.T,X) + b) #计算激活值,请参考公式2。
cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) #计算成本,请参考公式3和4。
#反向传播
dw = (1 / m) * np.dot(X, (A - Y).T) #请参考视频中的偏导公式。
db = (1 / m) * np.sum(A - Y) #请参考视频中的偏导公式。
#使用断言确保我的数据是正确的
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
#创建一个字典,把dw和db保存起来。
grads = {
"dw": dw,
"db": db
}
return (grads , cost)
def optimize(w , b , X , Y , num_iterations , learning_rate , print_cost = False):
"""
此函数通过运行梯度下降算法来优化w和b
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数组。
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
num_iterations - 优化循环的迭代次数
learning_rate - 梯度下降更新规则的学习率
print_cost - 每100步打印一次损失值
返回:
params - 包含权重w和偏差b的字典
grads - 包含权重和偏差相对于成本函数的梯度的字典
成本 - 优化期间计算的所有成本列表,将用于绘制学习曲线。
提示:
我们需要写下两个步骤并遍历它们:
1)计算当前参数的成本和梯度,使用propagate()。
2)使用w和b的梯度下降法则更新参数。
"""
costs = []
for i in range(num_iterations):
grads, cost = propagate(w, b, X, Y)
dw = grads["dw"]
db = grads["db"]
w = w - learning_rate * dw
b = b - learning_rate * db
#记录成本
if i % 100 == 0:
costs.append(cost)
#打印成本数据
if (print_cost) and (i % 100 == 0):
print("迭代的次数: %i , 误差值: %f" % (i,cost))
params = {
"w" : w,
"b" : b }
grads = {
"dw": dw,
"db": db }
return (params , grads , costs)
def predict(w , b , X ):
"""
使用学习逻辑回归参数logistic (w,b)预测标签是0还是1,
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数据
返回:
Y_prediction - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
"""
m = X.shape[1] #图片的数量
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0],1)
#计预测猫在图片中出现的概率
A = sigmoid(np.dot(w.T , X) + b)
for i in range(A.shape[1]):
#将概率a [0,i]转换为实际预测p [0,i]
Y_prediction[0,i] = 1 if A[0,i] > 0.5 else 0
#使用断言
assert(Y_prediction.shape == (1,m))
return Y_prediction
def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
"""
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train - numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train - numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test - numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test - numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations - 表示用于优化参数的迭代次数的超参数
learning_rate - 表示optimize()更新规则中使用的学习速率的超参数
print_cost - 设置为true以每100次迭代打印成本
返回:
d - 包含有关模型信息的字典。
"""
w , b = initialize_with_zeros(X_train.shape[0])
parameters , grads , costs = optimize(w , b , X_train , Y_train,num_iterations , learning_rate , print_cost)
#从字典“参数”中检索参数w和b
w , b = parameters["w"] , parameters["b"]
#预测测试/训练集的例子
Y_prediction_test = predict(w , b, X_test)
Y_prediction_train = predict(w , b, X_train)
#打印训练后的准确性
print("训练集准确性:" , format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100) ,"%")
print("测试集准确性:" , format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100) ,"%")
d = {
"costs" : costs,
"Y_prediction_test" : Y_prediction_test,
"Y_prediciton_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations" : num_iterations }
return d
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
浅层神经网络
神经网络的表示
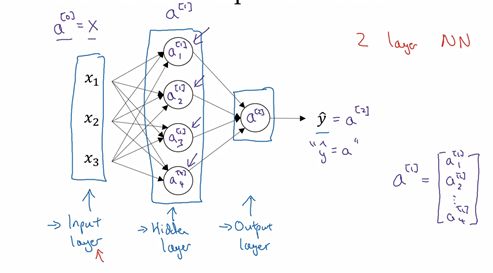
我们有输入特征 x 1 x_{1} x1、 x 2 x_{2} x2、 x 3 x_{3} x3,它们被竖直地堆叠起来,这叫做神经网络的输入层。它包含了神经网络的输入;然后这里有另外一层我们称之为隐藏层(图中的四个结点)。在本例中最后一层只由一个结点构成,而这个只有一个结点的层被称为输出层,它负责产生预测值。解释隐藏层的含义:在一个神经网络中,当你使用监督学习训练它的时候,训练集包含了输入也包含了目标输出,所以术语隐藏层的含义是在训练集中,这些中间结点的准确值我们是不知道到的,也就是说你看不见它们在训练集中应具有的值。你能看见输入的值,你也能看见输出的值,但是隐藏层中的东西,在训练集中你是无法看到的。所以这也解释了词语隐藏层,只是表示你无法在训练集中看到他们
现在我们再引入几个符号,就像我们之前用向量 x x x表示输入特征。这里有个可代替的记号 a [ 0 ] a^{[0]} a[0]可以用来表示输入特征。 a a a表示激活的意思,它意味着网络中不同层的值会传递到它们后面的层中,输入层将 x x x传递给隐藏层,所以我们将输入层的激活值称为 a [ 0 ] a^{[0]} a[0];下一层即隐藏层也同样会产生一些激活值,那么我将其记作 a [ 1 ] a^{[1]} a[1],所以具体地,这里的第一个单元或结点我们将其表示为 a 1 [ 0 ] a_{1}^{[0]} a1[0],第二个结点的值我们记为 a 2 [ 0 ] a_{2}^{[0]} a2[0]以此类推。所以这里的是一个四维的向量如果写成Python代码,那么它是一个规模为4x1的矩阵或一个大小为4的列向量,如下公式,它是四维的,因为在本例中,我们有四个结点或者单元,或者称为四个隐藏层单元;
最后输出层将产生某个数值 a a a,它只是一个单独的实数,所以 y ^ \widehat{y} y 值将取为 a [ 2 ] a^{[2]} a[2]。这与逻辑回归很相似,在逻辑回归中,我们有 y ^ \widehat{y} y 直接等于 a a a,在逻辑回归中我们只有一个输出层,所以我们没有用带方括号的上标。但是在神经网络中,我们将使用这种带上标的形式来明确地指出这些值来自于哪一层,有趣的是在约定俗成的符号传统中,在这里你所看到的这个例子,只能叫做一个两层的神经网络(图3.2.2)。原因是当我们计算网络的层数时,输入层是不算入总层数内,所以隐藏层是第一层,输出层是第二层。第二个惯例是我们将输入层称为第零层,所以在技术上,这仍然是一个三层的神经网络,因为这里有输入层、隐藏层,还有输出层。但是在传统的符号使用中,如果你阅读研究论文或者在这门课中,你会看到人们将这个神经网络称为一个两层的神经网络,因为我们不将输入层看作一个标准的层
最后,我们要看到的隐藏层以及最后的输出层是带有参数的,这里的隐藏层将拥有两个参数 W W W和 b b b,我将给它们加上上标 [ 1 ] ^{[1]} [1]( W [ 1 ] W^{[1]} W[1], b [ 1 ] b^{[1]} b[1]),表示这些参数是和第一层这个隐藏层有关系的。之后在这个例子中我们会看到是一个4x3的矩阵,而不是一个4x1的向量,第一个数字4源自于我们有四个结点或隐藏层单元,然后数字3源自于这里有三个输入特征,我们之后会更加详细地讨论这些矩阵的维数,到那时你可能就更加清楚了。相似的输出层也有一些与之关联的参数以及。从维数上来看,它们的规模分别是1x4以及1x1。1x4是因为隐藏层有四个隐藏层单元而输出层只有一个单元,之后我们会对这些矩阵和向量的维度做出更加深入的解释,所以现在你已经知道一个两层的神经网络什么样的了,即它是一个只有一个隐藏层的神经网络
计算一个神经网络的输出
上标表示神经网络的层数(隐藏层为1),下标表示该层的第几个神经元。这是神经网络的符号惯例
神经网络的计算
关于神经网络是怎么计算的,从我们之前提及的逻辑回归开始,如下图所示。用圆圈表示神经网络的计算单元,逻辑回归的计算有两个步骤,首先你按步骤计算出 z z z,然后在第二步中你以sigmoid函数为激活函数计算(得出),一个神经网络只是这样子做了好多次重复计算。
第一步,计算 z 1 [ 1 ] , z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] z_{1}^{[1]},z_{1}^{[1]}=w_{1}^{[1]T}x+b_{1}^{[1]} z1[1],z1[1]=w1[1]Tx+b1[1]。
第二步,通过激活函数计算 a 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) a_{1}^{[1]},a_{1}^{[1]}=\sigma(z_{1}^{[1]}) a1[1],a1[1]=σ(z1[1])。
隐藏层的第二个以及后面两个神经元的计算过程一样,只是注意符号表示不同,最终分别得到 a 2 [ 1 ] a_{2}^{[1]} a2[1]、 a 3 [ 1 ] a_{3}^{[1]} a3[1]、 a 4 [ 1 ] a_{4}^{[1]} a4[1],详细结果见下:
向量化计算 如果你执行神经网络的程序,用for循环来做这些看起来真的很低效。所以接下来我们要做的就是把这四个等式向量化。向量化的过程是将神经网络中的一层神经元参数纵向堆积起来,例如隐藏层中的 w w w纵向堆积起来变成一个 ( 4 , 3 ) (4,3) (4,3)的矩阵,用符号 W [ 1 ] W^{[1]} W[1]表示。另一个看待这个的方法是我们有四个逻辑回归单元,且每一个逻辑回归单元都有相对应的参数——向量 w w w,把这四个向量堆积在一起,你会得出这4×3的矩阵。
z [ n ] = w [ n ] x + b [ n ] z^{[n]}=w^{[n]}x+b^{[n]} z[n]=w[n]x+b[n]
a [ n ] = σ ( z [ n ] ) a^{[n]}=\sigma(z^{[n]}) a[n]=σ(z[n])
总结 通过本视频,你能够根据给出的一个单独的输入特征向量,运用四行代码计算出一个简单神经网络的输出。接下来你将了解的是如何一次能够计算出不止一个样本的神经网络输出,而是能一次性计算整个训练集的输出。
多样本向量化
逻辑回归是将各个训练样本组合成矩阵,对矩阵的各列进行计算。神经网络是通过对逻辑回归中的等式简单的变形,让神经网络计算出输出值。这种计算是所有的训练样本同时进行的,以下是实现它具体的步骤:
如果有一个非向量化形式的实现,而且要计算出它的预测值,对于所有训练样本,需要让 i i i从1到 m m m实现这四个等式:
对于上面的这个方程中的 ( i ) ^{(i)} (i),是所有依赖于训练样本的变量,即将 ( i ) (i) (i)添加到 x x x, z z z和 a a a。如果想计算 m m m个训练样本上的所有输出,就应该向量化整个计算,以简化这列
所以,希望通过这个细节可以更快地正确实现这些算法。接下来讲讲如何向量化这些:
将多个训练样本横向堆叠成一个矩阵 X X X,然后就可以推导出神经网络中前向传播(forward propagation)部分的向量化实现
激活函数
使用一个神经网络时,需要决定使用哪种激活函数用隐藏层上,哪种用在输出节点上。到目前为止,之前的视频只用过sigmoid激活函数,但是,有时其他的激活函数效果会更好
更通常的情况下,使用不同的函数 g ( z [ 1 ] ) g(z^{[1]}) g(z[1]), g g g可以是除了sigmoid函数以外的非线性函数。tanh函数或者双曲正切函数是总体上都优于sigmoid函数 a = t a n h ( z ) a=tanh(z) a=tanh(z)的值域是位于+1和-1之间。 a = t a n h ( z ) = e z − e − z e z + e − z a=tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} a=tanh(z)=ez+e−zez−e−z
事实上,tanh函数是sigmoid的向下平移和伸缩后的结果。对它进行了变形后,穿过了(0,0)点,并且值域介于+1和-1之间。
结果表明,如果在隐藏层上使用函数 g ( z [ 1 ] ) = t a n h ( z [ 1 ] ) g(z^{[1]})=tanh(z^{[1]}) g(z[1])=tanh(z[1]) 效果总是优于sigmoid函数。因为函数值域在-1和+1的激活函数,其均值是更接近零均值的。在训练一个算法模型时,如果使用tanh函数代替sigmoid函数中心化数据,使得数据的平均值更接近0而不是0.5.这会使下一层学习简单一点
在讨论优化算法时,有一点要说明:我基本已经不用sigmoid激活函数了,tanh函数在所有场合都优于sigmoid函数。
但有一个例外:在二分类的问题中,对于输出层,因为 y y y的值是0或1,所以想让 y ^ \widehat{y} y 的数值介于0和1之间,而不是在-1和+1之间。所以需要使用sigmoid激活函数。这里的 公式: g ( z [ 2 ] ) = σ ( z [ 2 ] ) g(z^{[2]})=\sigma(z^{[2]}) g(z[2])=σ(z[2]) 在这个例子里看到的是,对隐藏层使用tanh激活函数,输出层使用sigmoid函数。
所以,在不同的神经网络层中,激活函数可以不同
为了表示不同的激活函数,在不同的层中,使用方括号上标来指出 g g g上标为 [ 1 ] [1] [1]的激活函数,可能会跟 g g g上标为 [ 2 ] [2] [2]不同。方括号上标 [ 1 ] [1] [1]代表隐藏层,方括号上标 [ 2 ] [2] [2]表示输出层
sigmoid函数和tanh函数两者共同的缺点是,在 z z z特别大或者特别小的情况下,导数的梯度或者函数的斜率会变得特别小,最后就会接近于0,导致降低梯度下降的速度。
在机器学习另一个很流行的函数是:修正线性单元的函数(ReLu),ReLu函数图像是如下图。 公式: a = m a x ( 0 , z ) a=max(0,z) a=max(0,z) 所以,只要z是正值的情况下,导数恒等于1,当是z负值的时候,导数恒等于0。从实际上来说,当使用z的导数时,z=0的导数是没有定义的。但是当编程实现的时候,z的取值刚好等于0.00000001,这个值相当小,所以,在实践中,不需要担心这个值,z是等于0的时候,假设一个导数是1或者0效果都可以
这有一些选择激活函数的经验法则:
如果输出是0、1值(二分类问题),则输出层选择sigmoid函数,然后其它的所有单元都选择Relu函数。
这是很多激活函数的默认选择,如果在隐藏层上不确定使用哪个激活函数,那么通常会使用Relu激活函数。有时,也会使用tanh激活函数,但Relu的一个优点是:当z是负值的时候,导数等于0。
这里也有另一个版本的Relu被称为Leaky Relu
当z是负值时,这个函数的值不是等于0,而是轻微的倾斜,如图
这个函数通常比Relu激活函数效果要好,尽管在实际中Leaky ReLu使用的并不多
两者的优点是:
第一,在z的区间变动很大的情况下,激活函数的导数或者激活函数的斜率都会远大于0,在程序实现就是一个if-else语句,而sigmoid函数需要进行浮点四则运算,在实践中,使用ReLu激活函数神经网络通常会比使用sigmoid或者tanh激活函数学习的更快。
第二,sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于0,这会造成梯度弥散,而Relu和Leaky ReLu函数大于0部分都为常数,不会产生梯度弥散现象。(同时应该注意到的是,Relu进入负半区的时候,梯度为0,神经元此时不会训练,产生所谓的稀疏性,而Leaky ReLu不会有这问题)
z在ReLu的梯度一半都是0,但是,有足够的隐藏层使得z值大于0,所以对大多数的训练数据来说学习过程仍然可以很快。
快速概括一下不同激活函数的过程和结论。
sigmoid激活函数:除了输出层是一个二分类问题基本不会用它。
tanh激活函数:tanh是非常优秀的,几乎适合所有场合。
ReLu激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用ReLu或者Leaky ReLu。公式3.23: a = m a x ( 0.01 z , z ) a=max(0.01z,z) a=max(0.01z,z) 为什么常数是0.01?当然,可以为学习算法选择不同的参数。
在选择自己神经网络的激活函数时,有一定的直观感受,在深度学习中的经常遇到一个问题:在编写神经网络的时候,会有很多选择:隐藏层单元的个数、激活函数的选择、初始化权值……这些选择想得到一个对比较好的指导原则是挺困难的。
为自己的神经网络的应用测试这些不同的选择,会在以后检验自己的神经网络或者评估算法的时候,看到不同的效果。如果仅仅遵守使用默认的ReLu激活函数,而不要用其他的激励函数,那就可能在近期或者往后,每次解决问题的时候都使用相同的办法。
为什么需要非线性激活函数
我们稍后会谈到深度网络,有很多层的神经网络,很多隐藏层。事实证明,如果你使用线性激活函数或者没有使用一个激活函数,那么无论你的神经网络有多少层一直在做的只是计算线性函数,所以不如直接去掉全部隐藏层。
在我们的简明案例中,事实证明如果你在隐藏层用线性激活函数,在输出层用sigmoid函数,那么这个模型的复杂度和没有任何隐藏层的标准Logistic回归是一样的,如果你愿意的话,可以证明一下。
总而言之,不能在隐藏层用线性激活函数,可以用ReLU或者tanh或者leaky ReLU或者其他的非线性激活函数,唯一可以用线性激活函数的通常就是输出层;除了这种情况,会在隐层用线性函数的,除了一些特殊情况,比如与压缩有关的,那方面在这里将不深入讨论。在这之外,在隐层使用线性激活函数非常少见。因为房价都是非负数,所以我们也可以在输出层使用ReLU函数这样你的 y ^ \widehat{y} y 都大于等于0。
激活函数的导数
在神经网络中使用反向传播的时候,你真的需要计算激活函数的斜率或者导数。针对以下四种激活,求其导数如下:
- sigmoid activation function
其具体的求导如下: 公式: d d z g ( z ) = 1 1 + e − z ( 1 − 1 1 + e − z ) = g ( z ) ( 1 − g ( z ) ) \frac{d}{dz}g(z)=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=g(z)(1-g(z)) dzdg(z)=1+e−z1(1−1+e−z1)=g(z)(1−g(z))
注:
当 z = 10 z=10 z=10或 z = − 10 z=-10 z=−10; d d z g ( z ) ≈ 0 \frac{d}{dz}g(z)\approx0 dzdg(z)≈0
当 z = 0 z=0 z=0, d d z g ( z ) = g ( z ) ( 1 − g ( z ) ) = 1 / 4 \frac{d}{dz}g(z)=g(z)(1-g(z))=1/4 dzdg(z)=g(z)(1−g(z))=1/4
在神经网络中 a = g ( z ) ; g ( z ) ′ = d d z g ( z ) = a ( 1 − a ) a=g(z);g(z)^{'}=\frac{d}{dz}g(z)=a(1-a) a=g(z);g(z)′=dzdg(z)=a(1−a)
- Tanh activation function
其具体的求导如下: 公式: g ( z ) = t a n h ( z ) = e z − e − z e z + e − z g(z)=tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} g(z)=tanh(z)=ez+e−zez−e−z
d d z g ( z ) = 1 − ( t a n h ( z ) ) 2 \frac{d}{dz}g(z)=1-(tanh(z))^{2} dzdg(z)=1−(tanh(z))2
注:
当 z = 10 z=10 z=10或 z = − 10 z=-10 z=−10; d d z g ( z ) ≈ 0 \frac{d}{dz}g(z)\approx0 dzdg(z)≈0
当 z = 0 z=0 z=0, d d z g ( z ) = 1 − ( 0 ) = 1 \frac{d}{dz}g(z)=1-(0)=1 dzdg(z)=1−(0)=1
- Rectified Linear Unit (ReLU)
注:通常在z= 0的时候给定其导数1,0;当然z=0的情况很少
- Leaky linear unit (Leaky ReLU)
与ReLU类似
注:通常在 z = 0 z=0 z=0的时候给定其导数1,0.01;当然 z = 0 z=0 z=0的情况很少
神经网络的梯度下降(Gradient descent for neural networks)
你的单隐层神经网络会有 W [ 1 ] W^{[1]} W[1], b [ 1 ] b^{[1]} b[1], W [ 2 ] W^{[2]} W[2], b [ 2 ] b^{[2]} b[2]这些参数,还有 n x n_{x} nx个表示输入特征的个数, n [ 1 ] n^{[1]} n[1]表示隐藏单元个数, n [ 2 ] n^{[2]} n[2]表示输出单元个数。
在我们的例子中,我们只介绍过的这种情况,那么参数:
矩阵 W [ 1 ] W^{[1]} W[1]的维度就是( n [ 1 ] , n [ 0 ] n^{[1]},n^{[0]} n[1],n[0]), b [ 1 ] b^{[1]} b[1]就是 n [ 1 ] n^{[1]} n[1]维向量,可以写成 ( n [ 1 ] , 1 ) (n^{[1]},1) (n[1],1),就是一个的列向量。 W [ 2 ] W^{[2]} W[2]矩阵的维度就是( n [ 2 ] , n [ 1 ] n^{[2]},n^{[1]} n[2],n[1]), b [ 2 ] b^{[2]} b[2]的维度就是 ( n [ 2 ] , 1 ) (n^{[2]},1) (n[2],1)维度。
你还有一个神经网络的成本函数,假设你在做二分类任务,那么你的成本函数等于:
Cost function: 公式: J ( W [ 1 ] , b [ 1 ] , W [ 2 ] , b [ 2 ] ) = 1 m ∑ i = 1 m L ( y ^ , y ) J(W^{[1]},b^{[1]},W^{[2]},b^{[2]})=\frac{1}{m}\sum^{m}_{i=1}L(\widehat{y},y) J(W[1],b[1],W[2],b[2])=m1∑i=1mL(y ,y)
loss function和之前做logistic回归完全一样
训练参数需要做梯度下降,在训练神经网络的时候,随机初始化参数很重要,而不是初始化成全零。当你参数初始化成某些值后,每次梯度下降都会循环计算以下预测值:
y ^ ( i ) , ( i = 1 , 2 , . . . , m ) \widehat{y}^{(i)},(i=1,2,...,m) y (i),(i=1,2,...,m)
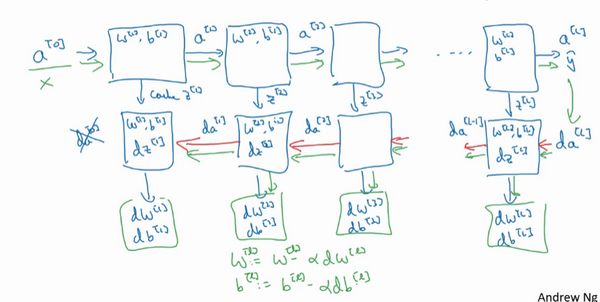
d W [ 1 ] = d J d W [ 1 ] dW^{[1]}=\frac{dJ}{dW^{[1]}} dW[1]=dW[1]dJ, d b [ 1 ] = d J d b [ 1 ] db^{[1]}=\frac{dJ}{db^{[1]}} db[1]=db[1]dJ, d W [ 2 ] = d J d W [ 2 ] dW^{[2]}=\frac{dJ}{dW^{[2]}} dW[2]=dW[2]dJ, d b [ 2 ] = d J d b [ 2 ] db^{[2]}=\frac{dJ}{db^{[2]}} db[2]=db[2]dJ
其中
W [ 1 ] ⇒ W [ 1 ] − a d W [ 1 ] , b [ 1 ] ⇒ b [ 1 ] − a d b [ 1 ] W^{[1]}\Rightarrow W^{[1]}-adW^{[1]},b^{[1]}\Rightarrow b^{[1]}-adb^{[1]} W[1]⇒W[1]−adW[1],b[1]⇒b[1]−adb[1]
W [ 2 ] ⇒ W [ 2 ] − a d W [ 2 ] , b [ 2 ] ⇒ b [ 2 ] − a d b [ 2 ] W^{[2]}\Rightarrow W^{[2]}-adW^{[2]},b^{[2]}\Rightarrow b^{[2]}-adb^{[2]} W[2]⇒W[2]−adW[2],b[2]⇒b[2]−adb[2]
forward propagation:
(1) z [ 1 ] = W [ 1 ] x + b [ 1 ] z^{[1]}=W^{[1]}x+b^{[1]} z[1]=W[1]x+b[1]
(2) a [ 1 ] = σ ( z [ 1 ] ) a^{[1]}=\sigma(z^{[1]}) a[1]=σ(z[1])
(3) z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ] z^{[2]}=W^{[2]}a^{[1]}+b^{[2]} z[2]=W[2]a[1]+b[2]
(4) a [ 2 ] = g [ 2 ] ( z ∣ z ∣ ) = σ ( z [ 2 ] ) a^{[2]}=g^{[2]}(z^{|z|})=\sigma(z^{[2]}) a[2]=g[2](z∣z∣)=σ(z[2])
反向传播方程如下:
back propagation:
d z [ 2 ] = A [ 2 ] − Y , Y = [ y [ 1 ] , y [ 2 ] , . . . , y [ m ] ] dz^{[2]}=A^{[2]}-Y,Y=[y^{[1]},y^{[2]},...,y^{[m]}] dz[2]=A[2]−Y,Y=[y[1],y[2],...,y[m]]
d W [ 2 ] = 1 m d z [ 2 ] A [ 1 ] T dW^{[2]}=\frac{1}{m}dz^{[2]}A^{[1]T} dW[2]=m1dz[2]A[1]T
d b [ 2 ] = 1 m n p . d u m ( d z [ 2 ] , a x i s = 1 , k e e p d i m s = T r u e ) db^{[2]}=\frac{1}{m}np.dum(dz^{[2]},axis=1,keepdims=True) db[2]=m1np.dum(dz[2],axis=1,keepdims=True)
d W [ 1 ] = 1 m d z [ 1 ] x T dW^{[1]}=\frac{1}{m}dz^{[1]}x^{T} dW[1]=m1dz[1]xT
上述是反向传播的步骤,注:这些都是针对所有样本进行过向量化
Y Y Y是 1 × m 1\times m 1×m的矩阵,这里np.sum是python的numpy命令,axis=1表示水平相加求和,keepdims是防止python输出那些古怪的秩数 ( n , ) (n,) (n,),加上这个确保阵矩阵 d b [ 2 ] db^{[2]} db[2]这个向量输出的维度为 ( n , 1 ) (n,1) (n,1)这样标准的形式。
目前为止,我们计算的都和Logistic回归十分相似,但当你开始计算反向传播时,你需要计算,是隐藏层函数的导数,输出在使用sigmoid函数进行二元分类
还有一种防止python输出奇怪的秩数,需要显式地调用reshape把np.sum输出结果写成矩阵形式。
如果你要实现这些算法,你必须正确执行正向和反向传播运算,你必须能计算所有需要的导数,用梯度下降来学习神经网络的参数
随机初始化
当你训练神经网络时,权重随机初始化是很重要的。对于逻辑回归,把权重初始化为0当然也是可以的。但是对于一个神经网络,如果你把权重或者参数都初始化为0,那么梯度下降将不会起作用。
由此可以推导,如果你把权重都初始化为0,那么由于隐含单元开始计算同一个函数,所有的隐含单元就会对输出单元有同样的影响。一次迭代后同样的表达式结果仍然是相同的,即隐含单元仍是对称的。通过推导,两次、三次、无论多少次迭代,不管你训练网络多长时间,隐含单元仍然计算的是同样的函数。因此这种情况下超过1个隐含单元也没什么意义,因为他们计算同样的东西。当然更大的网络,比如你有3个特征,还有相当多的隐含单元。
如果你要初始化成0,由于所有的隐含单元都是对称的,无论你运行梯度下降多久,他们一直计算同样的函数。这没有任何帮助,因为你想要两个不同的隐含单元计算不同的函数,这个问题的解决方法就是随机初始化参数。
你应该这么做:把 W [ 1 ] W^{[1]} W[1]设为np.random.randn(2,2)(生成高斯分布),通常再乘上一个小的数,比如0.01,这样把它初始化为很小的随机数。然后 b b b没有这个对称的问题(叫做symmetry breaking problem),所以可以把 b b b初始化为0,因为只要随机初始化 W W W你就有不同的隐含单元计算不同的东西,因此不会有symmetry breaking问题了。相似的,对于你可以随机初始化, b [ 2 ] b^{[2]} b[2]可以初始化为0。
你也许会疑惑,这个常数从哪里来,为什么是0.01,而不是100或者1000。我们通常倾向于初始化为很小的随机数。因为如果你用tanh或者sigmoid激活函数,或者说只在输出层有一个Sigmoid,如果(数值)波动太大,当你计算激活值时 z [ 1 ] = W [ 1 ] x + b [ 1 ] , a [ 1 ] = σ ( z [ 1 ] ) = g [ 1 ] ( z [ 1 ] ) z^{[1]}=W^{[1]}x+b^{[1]},a^{[1]}=\sigma(z^{[1]})=g^{[1]}(z^{[1]}) z[1]=W[1]x+b[1],a[1]=σ(z[1])=g[1](z[1])如果 W W W很大, z z z就会很大或者很小,因此这种情况下你很可能停在tanh/sigmoid函数的平坦的地方,这些地方梯度很小也就意味着梯度下降会很慢,因此学习也就很慢。
回顾一下:如果 w w w很大,那么你很可能最终停在(甚至在训练刚刚开始的时候) z z z很大的值,这会造成tanh/Sigmoid激活函数饱和在龟速的学习上,如果你没有sigmoid/tanh激活函数在你整个的神经网络里,就不成问题。但如果你做二分类并且你的输出单元是Sigmoid函数,那么你不会想让初始参数太大,因此这就是为什么乘上0.01或者其他一些小数是合理的尝试。对于 w [ 2 ] w^{[2]} w[2]一样,就是np.random.randn((1,2)),我猜会是乘以0.01。
事实上有时有比0.01更好的常数,当你训练一个只有一层隐藏层的网络时(这是相对浅的神经网络,没有太多的隐藏层),设为0.01可能也可以。但当你训练一个非常非常深的神经网络,你可能要试试0.01以外的常数。下一节课我们会讨论怎么并且何时去选择一个不同于0.01的常数,但是无论如何它通常都会是个相对小的数。
应用
np.sum(A, axis = 1, keepdims = True)
#axis=1 以竖轴为基准,同行相加
#keepdims保持矩阵的二维特性
如果为所有隐藏的单位建立了一个使用tanh激活的网络。使用np.random.randn(…, …)*1000将权重初始化为相对较大的值。会发生什么?
这将导致tanh的输入也非常大,从而导致梯度接近于零。因此,优化算法将变得缓慢。
深层神经网络(Deep Neural Network)
深层神经网络
前向传播和反向传播
前向传播,输入 a [ l − 1 ] a^{[l-1]} a[l−1],输出是 a [ l ] a^{[l]} a[l],缓存为 z [ l ] z^{[l]} z[l];从实现的角度来说我们可以缓存下 w [ l ] w^{[l]} w[l]和 b [ l ] b^{[l]} b[l],这样更容易在不同的环节中调用函数。
下面讲反向传播的步骤:
输入为 d a [ l ] da^{[l]} da[l],输出为 d a [ l − 1 ] da^{[l-1]} da[l−1], d w [ l ] dw^{[l]} dw[l], d b [ l ] db^{[l]} db[l]
深层网络中的前向传播
可以使用For循环实现
向量化实现过程可以写成:
Z [ l ] = W [ l ] a [ l − 1 ] + b [ l ] , A [ l ] = g [ l ] ( Z [ l ] ) ( A [ 0 ] = X ) Z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]},A^{[l]}=g^{[l]}(Z^{[l]})\quad(A^{[0]}=X) Z[l]=W[l]a[l−1]+b[l],A[l]=g[l](Z[l])(A[0]=X)
这里只能用一个显式for循环, l l l从1到 L L L,然后一层接着一层去计算
深层网络中的反向传播
核对矩阵的维数
当实现深度神经网络的时候,其中一个我常用的检查代码是否有错的方法就是拿出一张纸过一遍算法中矩阵的维数。
w w w的维度是(下一层的维数,前一层的维数),即: w [ l ] : ( n [ l ] , n [ l − 1 ] ) w^{[l]}:(n^{[l]},n^{[l-1]}) w[l]:(n[l],n[l−1])
b b b的维度是(下一层的维数,1),即:
b [ l ] : ( n [ l ] , 1 ) ; b^{[l]}:(n^{[l]},1); b[l]:(n[l],1);
z [ l ] , a [ l ] : ( n [ l ] , 1 ) z^{[l]},a^{[l]}:(n^{[l]},1) z[l],a[l]:(n[l],1)
d w [ l ] dw^{[l]} dw[l]和 w [ l ] w^{[l]} w[l]维度相同, d b [ l ] db^{[l]} db[l]和 b [ l ] b^{[l]} b[l]维度相同,且 w w w和 b b b向量化维度不变,但 z z z, a a a以及 x x x的维度会向量化后发生变化
向量化后:
Z [ l ] Z^{[l]} Z[l]可以看成由每一个单独的 Z [ l ] Z^{[l]} Z[l]叠加而得到, Z [ l ] = ( z [ l ] [ 1 ] , z [ l ] [ 2 ] , z [ l ] [ 3 ] , . . . , z [ l ] [ m ] ) Z^{[l]}=(z^{[l][1]},z^{[l][2]},z^{[l][3]},...,z^{[l][m]}) Z[l]=(z[l][1],z[l][2],z[l][3],...,z[l][m])
m m m为训练集大小,所以 Z [ l ] 的 Z^{[l]}的 Z[l]的维度不再是 ( n [ l ] , 1 ) (n^{[l]},1) (n[l],1),而是 ( n [ l ] , m ) (n^{[l]},m) (n[l],m)。
A [ l ] : ( n [ l ] , m ) A^{[l]}:(n^{[l]},m) A[l]:(n[l],m), A [ 0 ] = X = ( n [ l ] , m ) A^{[0]}=X=(n^{[l]},m) A[0]=X=(n[l],m)
在你做深度神经网络的反向传播时,一定要确认所有的矩阵维数是前后一致的,可以大大提高代码通过率
为什么使用深层表示
为什么深层的网络在很多问题上比浅层的好?
其实并不需要很大的神经网络,但是得有深度,得有比较多的隐藏层,这是为什么呢?
首先,深度网络究竟在计算什么?如果你在建一个人脸识别或是人脸检测系统,深度神经网络所做的事就是,当你输入一张脸部的照片,然后你可以把深度神经网络的第一层,当成一个特征探测器或者边缘探测器。
所以深度神经网络的这许多隐藏层中,较早的前几层能学习一些低层次的简单特征,等到后几层,就能把简单的特征结合起来,去探测更加复杂的东西。比如你录在音频里的单词、词组或是句子,然后就能运行语音识别了。同时我们所计算的之前的几层,也就是相对简单的输入函数,比如图像单元的边缘什么的。到网络中的深层时,你实际上就能做很多复杂的事,比如探测面部或是探测单词、短语或是句子。
神经网络的更深层通常比前面的层计算更复杂的特征
搭建神经网络快
参数 VS 超参数
实际上深度学习有很多不同的超参数,之后我们也会介绍一些其他的超参数,如momentum、mini batch size、regularization parameters等等
如何寻找超参数的最优值?
在前面几页中,还有很多不同的超参数。然而,当你开始开发新应用时,预先很难确切知道,究竟超参数的最优值应该是什么。所以通常,你必须尝试很多不同的值,并走这个循环,试试各种参数。试试看5个隐藏层,这个数目的隐藏单元,实现模型并观察是否成功,然后再迭代。这页的标题是,应用深度学习领域,一个很大程度基于经验的过程,凭经验的过程通俗来说,就是试直到你找到合适的数值。
然后其次,甚至是你已经用了很久的模型,可能你在做网络广告应用,在你开发途中,很有可能学习率的最优数值或是其他超参数的最优值是会变的,所以即使你每天都在用当前最优的参数调试你的系统,你还是会发现,最优值过一年就会变化,因为电脑的基础设施,CPU或是GPU可能会变化很大。所以有一条经验规律可能每几个月就会变。如果你所解决的问题需要很多年时间,只要经常试试不同的超参数,勤于检验结果,看看有没有更好的超参数数值,相信你慢慢会得到设定超参数的直觉,知道你的问题最好用什么数值。
应用
区分python中np.multiply()、np.dot()和星号(*)三种乘法运算的区别
np.multiply():数组和矩阵对应位置相乘,输出与相乘数组/矩阵的大小一致
np.dot():对于秩为1的数组(一维),执行对应位置相乘,然后再相加;
对于秩不为1的二维数组,执行矩阵乘法运算;超过二维的可以参考numpy库介绍。
星号(*)乘法运算:对数组执行对应位置相乘;对矩阵(np.mat())执行矩阵乘法运算
import numpy as np
import h5py
import matplotlib.pyplot as plt
import testCases
from dnn_utils import sigmoid,sigmoid_backward,relu,relu_backward
import lr_utils
#指定随机种子
#利用随机数种子,每次生成的随机数相同
np.random.seed(1)
#一、初始化参数
def initialize_parameters(n_x,n_h,n_y):
"""
此函数是为了初始化两层网络参数而使用的函数
:param n_x: 输入层节点数量
:param n_h: 隐藏层节点数量
:param n_y: 输出层节点数量
:return: parameters - 包含你的参数的python字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros((n_y,1))
#使用断言确保我的数据格式是正确的
assert (W1.shape == (n_h,n_x))
assert (b1.shape == (n_h,1))
assert (W2.shape == (n_y,n_h))
assert (b2.shape == (n_y,1))
parameters = {
"W1":W1,
"b1":b1,
"W2":W2,
"b2":b2}
return parameters
def initialize_parameters_deep(layers_dims):
"""
此函数是为了初始化多层网络参数而使用的函数
:param layers_dims:包含我们网络中每个图层的节点数量的列表
:return:parameters - 包含参数“W1”,“b1”,...,“WL”,“bL”的字典:
W1 - 权重矩阵,维度为(layers_dims [1],layers_dims [1-1])
bl - 偏向量,维度为(layers_dims [1],1)
"""
np.random.seed(3)
parameters={}
L = len(layers_dims)
for l in range(1,L):
parameters["W"+str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1]) / np.sqrt(layers_dims[l-1])
parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))
# 确保我要的数据的格式是正确的
assert (parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l - 1]))
assert (parameters["b" + str(l)].shape == (layers_dims[l], 1))
return parameters
# 二、前向传播函数
def linear_forward(A, W, b):
"""
实现前向传播的线性部分。
参数:
A - 来自上一层(或输入数据)的激活,维度为(上一层的节点数量,示例的数量)
W - 权重矩阵,numpy数组,维度为(当前图层的节点数量,前一图层的节点数量)
b - 偏向量,numpy向量,维度为(当前图层节点数量,1)
返回:
Z - 激活功能的输入,也称为预激活参数
cache - 一个包含“A”,“W”和“b”的字典,存储这些变量以有效地计算后向传递
"""
Z = np.dot(W, A) + b
assert (Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
def linear_activation_forward(A_prev,W,b,activation):
"""
实现LINEAR-> ACTIVATION 这一层的前向传播
参数:
A_prev - 来自上一层(或输入层)的激活,维度为(上一层的节点数量,示例数)
W - 权重矩阵,numpy数组,维度为(当前层的节点数量,前一层的大小)
b - 偏向量,numpy阵列,维度为(当前层的节点数量,1)
activation - 选择在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
A - 激活函数的输出,也称为激活后的值
cache - 一个包含“linear_cache”和“activation_cache”的字典,我们需要存储它以有效地计算后向传递
"""
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A,cache
def L_model_forward(X, parameters):
"""
实现[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID计算前向传播,也就是多层网络的前向传播,为后面每一层都执行LINEAR和ACTIVATION
参数:
X - 数据,numpy数组,维度为(输入节点数量,示例数)
parameters - initialize_parameters_deep()的输出
返回:
AL - 最后的激活值
caches - 包含以下内容的缓存列表:
linear_relu_forward()的每个cache(有L-1个,索引为从0到L-2)
linear_sigmoid_forward()的cache(只有一个,索引为L-1)
"""
caches = []
A = X
L = len(parameters) // 2
for l in range(1,L):
A_prev = A
A, cache = linear_activation_forward(A_prev,parameters['W'+str(l)],parameters['b'+str(l)],"relu")
caches.append(cache)
AL, cache = linear_activation_forward(A,parameters['W' + str(L)],parameters['b' + str(L)], "sigmoid")
caches.append(cache)
assert (AL.shape == (1,X.shape[1]))
return AL,caches
# 三、计算成本
def compute_cost(AL,Y):
"""
实施等式(4)定义的成本函数。
参数:
AL - 与标签预测相对应的概率向量,维度为(1,示例数量)
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
返回:
cost - 交叉熵成本
"""
m = Y.shape[1]
#np.sum(np.multiply(np.mat(A),np.mat(B))) #输出为标量
cost = -np.sum(np.multiply(np.log(AL),Y)+np.multiply(np.log(1-AL),(1-Y))) / m
cost = np.squeeze(cost)
assert (cost.shape == ())
return cost
# 四、反向传播
def linear_backward(dZ,cache):
"""
为单层实现反向传播的线性部分(第L层)
参数:
dZ - 相对于(当前第l层的)线性输出的成本梯度
cache - 来自当前层前向传播的值的元组(A_prev,W,b)
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度,与W的维度相同
db - 相对于b(当前层l)的成本梯度,与b维度相同
"""
A_prev,W,b = cache
m = A_prev.shape[1]
dW = np.dot(dZ,A_prev.T) / m
db = np.sum(dZ,axis=1,keepdims=True) / m
dA_prev = np.dot(W.T,dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev,dW,db
def linear_activation_backward(dA, cache, activation="relu"):
"""
实现LINEAR-> ACTIVATION层的后向传播。
参数:
dA - 当前层l的激活后的梯度值
cache - 我们存储的用于有效计算反向传播的值的元组(值为linear_cache,activation_cache)
activation - 要在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度值,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度值,与W的维度相同
db - 相对于b(当前层l)的成本梯度值,与b的维度相同
"""
linear_cache,activation_cache = cache
if activation == "sigmoid":
dZ = sigmoid_backward(dA,activation_cache)
dA_prev ,dW,db = linear_backward(dZ,linear_cache)
elif activation == "relu":
dZ = relu_backward(dA,activation_cache)
dA_prev,dW,db = linear_backward(dZ,linear_cache)
return dA_prev,dW,db
def L_model_backward(AL, Y, caches):
"""
对[LINEAR-> RELU] *(L-1) - > LINEAR - > SIGMOID组执行反向传播,就是多层网络的向后传播
参数:
AL - 概率向量,正向传播的输出(L_model_forward())
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
caches - 包含以下内容的cache列表:
linear_activation_forward("relu")的cache,不包含输出层
linear_activation_forward("sigmoid")的cache
返回:
grads - 具有梯度值的字典
grads [“dA”+ str(l)] = ...
grads [“dW”+ str(l)] = ...
grads [“db”+ str(l)] = ...
"""
grads={}
L = len(caches)
m = AL.shape[1]
Y = Y.reshape(AL.shape)
dAL = -(np.divide(Y,AL) - np.divide(1-Y,1-AL))
current_cache = caches[L-1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, "sigmoid")
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, "relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
# 五、更新参数
def update_parameters(parameters, grads, learning_rate):
"""
使用梯度下降更新参数
参数:
parameters - 包含你的参数的字典
grads - 包含梯度值的字典,是L_model_backward的输出
返回:
parameters - 包含更新参数的字典
参数[“W”+ str(l)] = ...
参数[“b”+ str(l)] = ...
"""
L = len(parameters) // 2 # 整除
for l in range(L):
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
## 搭建两层的神经网络
def two_layer_model(X,Y,layers_dims,learning_rate=0.0075,num_iterations=3000,print_cost=False,isPlot=True):
"""
实现一个两层的神经网络,【LINEAR->RELU】-> 【LINEAR -> SIGMOID】
:param X: 输入的数据,维度为(n_x,例子数)
:param Y: 标签,向量,0为非猫,1为猫,维度为(1,数量)
:param layers_dims: 层数的向量,维度为(n_y,n_h,n_y)
:param learning_rate: 学习率
:param num_iterations: 迭代的次数
:param print_cost: 是否打印成本值,每100次打印一次
:param isPlot: 是否绘制出误差值的图谱
:return: parameters - 一个包含W1,b1,W2,b2的字典变量
"""
np.random.seed(1)
grads={}
costs=[]
(n_x,n_h,n_y)=layers_dims
"""
初始化参数
"""
parameters = initialize_parameters(n_x,n_h,n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
"""
开始进行迭代
"""
for i in range(0,num_iterations):
#前向传播
A1,cache1 = linear_activation_forward(X,W1,b1,"relu")
A2,cache2 = linear_activation_forward(A1,W2,b2,"sigmoid")
#计算成本
cost = compute_cost(A2,Y)
#反向传播
## 初始化后向传播
dA2 = -(np.divide(Y,A2)-np.divide(1-Y,1-A2))
## 反向传播,输入:“dA2,cache2,cache1”。 输出:“dA1,dW2,db2;还有dA0(未使用),dW1,db1”。
dA1,dW2,db2 = linear_activation_backward(dA2,cache2,"sigmoid")
dA0,dW1,db1 = linear_activation_backward(dA1,cache1,"relu")
##向后传播完成后的数据保存在grads
grads["dW1"] = dW1
grads["db1"] = db1
grads["dW2"] = dW2
grads["db2"] = db2
#更新参数
parameters = update_parameters(parameters,grads,learning_rate)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
#打印成本值,如果print_cost=False则忽略
if i% 100 == 0:
#记录成本
costs.append(cost)
#是否打印成本值
if print_cost:
print("第", i, "次迭代,成本值为:", np.squeeze(cost))
#完成迭代,根据条件绘制图
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 返回parameters
return parameters
# 加载图像数据集,并训练
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()
train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y
n_x = 12288
n_h = 7
n_y = 1
layers_dims = (n_x,n_h,n_y)
parameters = two_layer_model(train_x, train_set_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True,isPlot=True)
#迭代完成,进行预测
def predict(X, y, parameters):
"""
该函数用于预测L层神经网络的结果,当然也包含两层
参数:
X - 测试集
y - 标签
parameters - 训练模型的参数
返回:
p - 给定数据集X的预测
"""
m = X.shape[1]
n = len(parameters) // 2 # 神经网络的层数
p = np.zeros((1, m))
# 根据参数前向传播
probas, caches = L_model_forward(X, parameters)
for i in range(0, probas.shape[1]):
if probas[0, i] > 0.5:
p[0, i] = 1
else:
p[0, i] = 0
print("准确度为: " + str(float(np.sum((p == y)) / m)))
return p
#预测,查看训练集和测试集的准确性
predictions_train = predict(train_x, train_y, parameters) #训练集
predictions_test = predict(test_x, test_y, parameters) #测试集
# 搭建多层的神经网络
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False,isPlot=True):
"""
实现一个L层神经网络:[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID
:param X:输入的数据,维度为(n_x,例子数)
:param Y:标签,向量,0为非猫,1为猫,维度为(1,数量)
:param layers_dims:层数的向量,维度为(n_y,n_h,···,n_h,n_y)
:param learning_rate:学习率
:param num_iterations:迭代的次数
:param print_cost:是否打印成本值,每100次打印一次
:param isPlot: 是否绘制出误差值的图谱
:return:parameters - 模型学习的参数。 然后他们可以用来预测
"""
np.random.seed(1)
costs=[]
parameters=initialize_parameters_deep(layers_dims)
for i in range(0,num_iterations):
AL,caches = L_model_forward(X,parameters)
cost = compute_cost(AL,Y)
grads = L_model_backward(AL,Y,caches)
parameters = update_parameters(parameters,grads,learning_rate)
# 打印成本值,如果print_cost=False则忽略
if i % 100 == 0:
# 记录成本
costs.append(cost)
# 是否打印成本值
if print_cost:
print("第", i, "次迭代,成本值为:", np.squeeze(cost))
# 迭代完成,根据条件绘制图
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
## 加载图像数据集,并训练
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()
train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y
layers_dims = [12288,20,7,5,1] #5层model
parameters = L_layer_model(train_x,train_y,layers_dims,num_iterations=2500,print_cost=True,isPlot=True)
#看预测效果
pred_train = predict(train_x, train_y, parameters) #训练集
pred_test = predict(test_x, test_y, parameters) #测试集
# 从70%到72%再到78%准确度在一点点增加,当然,你也可以手动的去调整layers_dims,准确度可能又会提高一些
深度学习的实用层面
训练、验证、测试集(Train/ Dev / Test sets)
应用深度学习是一个典型的迭代过程,需要多次循环往复,才能为应用程序找到一个称心的神经网络,因此循环该过程的效率是决定项目进展速度的一个关键因素,而创建高质量的训练数据集,验证集和测试集也有助于提高循环效率
假设这是训练数据,我用一个长方形表示,我们通常会将这些数据划分成几部分,一部分作为训练集,一部分作为简单交叉验证集,有时也称之为验证集,方便起见,我就叫它验证集(dev set),其实都是同一个概念,最后一部分则作为测试集
接下来,我们开始对训练执行算法,通过验证集或简单交叉验证集选择最好的模型,经过充分验证,我们选定了最终模型,然后就可以在测试集上进行评估了,为了无偏评估算法的运行状况
在大数据时代,我们现在的数据量可能是百万级别,那么验证集和测试集占数据总量的比例会趋向于变得更小。因为验证集的目的就是验证不同的算法,检验哪种算法更有效,因此,验证集要足够大才能评估,比如2个甚至10个不同算法,并迅速判断出哪种算法更有效。我们可能不需要拿出20%的数据作为验证集
比如我们有100万条数据,那么取1万条数据便足以进行评估,找出其中表现最好的1-2种算法。同样地,根据最终选择的分类器,测试集的主要目的是正确评估分类器的性能,所以,如果拥有百万数据,我们只需要1000条数据,便足以评估单个分类器,并且准确评估该分类器的性能。
总结一下,在机器学习中,我们通常将样本分成训练集,验证集和测试集三部分,数据集规模相对较小,适用传统的划分比例,数据集规模较大的,验证集和测试集要小于数据总量的20%或10%。后面我会给出如何划分验证集和测试集的具体指导。
根据经验,我建议大家要确保验证集和测试集的数据来自同一分布。因为你们要用验证集来评估不同的模型,尽可能地优化性能。如果验证集和测试集来自同一个分布就会很好
最后一点,就算没有测试集也不要紧,测试集的目的是对最终所选定的神经网络系统做出无偏估计,如果不需要无偏估计,也可以不设置测试集。所以如果只有验证集,没有测试集,我们要做的就是,在训练集上训练,尝试不同的模型框架,在验证集上评估这些模型,然后迭代并选出适用的模型。因为验证集中已经涵盖测试集数据,其不再提供无偏性能评估。当然,如果你不需要无偏估计,那就再好不过了。
在机器学习中,如果只有一个训练集和一个验证集,而没有独立的测试集,遇到这种情况,训练集还被人们称为训练集,而验证集则被称为测试集,不过在实际应用中,人们只是把测试集当成简单交叉验证集使用,并没有完全实现该术语的功能,因为他们把验证集数据过度拟合到了测试集中。
偏差,方差(Bias / Variance)
理解偏差和方差的两个关键数据是训练集误差(Train set error)和验证集误差(Dev set error)
我们之前讲过,这样的分类器,会产生高偏差,因为它的数据拟合度低,像这种接近线性的分类器,数据拟合度低
但是如果我们稍微改变一下分类器,我用紫色笔画出,它会过度拟合部分数据,用紫色线画出的分类器具有高偏差和高方差,偏差高是因为它几乎是一条线性分类器,并未拟合数据
这种二次曲线能够很好地拟合数据
总结一下,我们讲了如何通过分析在训练集上训练算法产生的误差和验证集上验证算法产生的误差来诊断算法是否存在高偏差和高方差,是否两个值都高,或者两个值都不高,根据算法偏差和方差的具体情况决定接下来你要做的工作
机器学习基础
下图就是我在训练神经网络用到的基本方法:(尝试这些方法,可能有用,可能没用)
第一点,高偏差和高方差是两种不同的情况,我们后续要尝试的方法也可能完全不同,我通常会用训练验证集来诊断算法是否存在偏差或方差问题,然后根据结果选择尝试部分方法。举个例子,如果算法存在高偏差问题,准备更多训练数据其实也没什么用处,至少这不是更有效的方法,所以大家要清楚存在的问题是偏差还是方差,还是两者都有问题,明确这一点有助于我们选择出最有效的方法。
第二点,在机器学习的初期阶段,关于所谓的偏差方差权衡的讨论屡见不鲜,原因是我们能尝试的方法有很多。可以增加偏差,减少方差,也可以减少偏差,增加方差,但是在深度学习的早期阶段,我们没有太多工具可以做到只减少偏差或方差却不影响到另一方。但在当前的深度学习和大数据时代,只要持续训练一个更大的网络,只要准备了更多数据,那么也并非只有这两种情况,我们假定是这样,那么,只要正则适度,通常构建一个更大的网络便可以,在不影响方差的同时减少偏差,而采用更多数据通常可以在不过多影响偏差的同时减少方差。这两步实际要做的工作是:训练网络,选择网络或者准备更多数据,现在我们有工具可以做到在减少偏差或方差的同时,不对另一方产生过多不良影响。我觉得这就是深度学习对监督式学习大有裨益的一个重要原因,也是我们不用太过关注如何平衡偏差和方差的一个重要原因,但有时我们有很多选择,减少偏差或方差而不增加另一方。最终,我们会得到一个非常规范化的网络。从下节课开始,我们将讲解正则化,训练一个更大的网络几乎没有任何负面影响,而训练一个大型神经网络的主要代价也只是计算时间,前提是网络是比较规范化的。
正则化
深度学习可能存在过拟合问题——高方差,有两个解决方法,一个是正则化,另一个是准备更多的数据,这是非常可靠的方法,但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高,但正则化通常有助于避免过拟合或减少你的网络误差。但你可能无法时时准备足够多的训练数据,或者,获取更多数据的成本很高,但正则化有助于避免过度拟合,或者减少网络误差,下面我们就来讲讲正则化的作用原理
在逻辑回归函数中加入正则化,只需添加参数λ,也就是正则化参数
λ 2 m \frac{\lambda}{2m} 2mλ乘以 w w w范数的平方, w w w欧几里德范数的平方等于 w j w_{j} wj( j j j值从1到 n x n_{x} nx)平方的和
上图此方法称为 L 2 L2 L2正则化。因为这里用了欧几里德法线,被称为向量参数 w w w的 L 2 L2 L2范数。
为什么只正则化参数 w w w?为什么不再加上参数 b b b呢?你可以这么做,只是我习惯省略不写,因为** w w w通常是一个高维参数矢量**,已经可以表达高偏差问题, w w w可能包含有很多参数,我们不可能拟合所有参数,而 b b b只是单个数字,所以w几乎涵盖所有参数,而b不是,如果加了参数b,其实也没太大影响,因为 b b b只是众多参数中的一个,所以我通常省略不计,如果你想加上这个参数,完全没问题。
L 2 L2 L2正则化是最常见的正则化类型,你们可能听说过 L 1 L1 L1正则化, L 1 L1 L1正则化,加的不是 L 2 L2 L2范数,而是正则项 λ m \frac{\lambda}{m} mλ乘以 ∑ j = 1 n x ∣ w ∣ \sum_{j=1}^{n_{x}}|w| ∑j=1nx∣w∣, ∑ j = 1 n x ∣ w ∣ \sum_{j=1}^{n_{x}}|w| ∑j=1nx∣w∣也被称为参数 w w w向量的 L 1 L1 L1范数,无论分母是 m m m还是 2 m 2m 2m,它都是一个比例常量。
如果用的是 L 1 L1 L1正则化, w w w最终会是稀疏的,也就是说 w w w向量中有很多0,有人说这样有利于压缩模型,因为集合中参数均为0,存储模型所占用的内存更少。实际上,虽然 L 1 L1 L1正则化使模型变得稀疏,却没有降低太多存储内存,所以我认为这并不是 L 1 L1 L1正则化的目的,至少不是为了压缩模型,人们在训练网络时,越来越倾向于使用 L 2 L2 L2正则化。
λ是另外一个需要调整的超级参数,为了方便写代码,在Python编程语言中,λ是一个保留字段,编写代码时,我们删掉 a a a,写成 l a m b d lambd lambd,以免与Python中的保留字段冲突,这就是在逻辑回归函数中实现 L 2 L2 L2正则化的过程,如何在神经网络中实现 L 2 L2 L2正则化呢?
![]()
神经网络含有一个成本函数,该函数包含 W [ 1 ] W^{[1]} W[1], b [ 1 ] b^{[1]} b[1]到 W [ l ] W^{[l]} W[l], b l b^{l} bl所有参数,字母 L L L是神经网络所含的层数,因此成本函数等于 m m m个训练样本损失函数的总和乘以 1 m \frac{1}{m} m1,正则项为 λ 2 m ∑ 1 L ∣ W [ l ] ∣ 2 \frac{\lambda}{2m}\sum_{1}^{L}|W^{[l]}|^{2} 2mλ∑1L∣W[l]∣2,我们称 ∣ ∣ W [ l ] ∣ ∣ 2 ||W^{[l]}||^{2} ∣∣W[l]∣∣2为范数平方,这个 ∣ ∣ W [ l ] ∣ ∣ 2 ||W^{[l]}||^{2} ∣∣W[l]∣∣2矩阵范数(即平方范数),被定义为矩阵中所有元素的平方求和,
该矩阵范数被称作“弗罗贝尼乌斯范数”,用下标 F F F标注,鉴于线性代数中一些神秘晦涩的原因,我们不称之为“矩阵 L 2 L2 L2范数”,而称它为“弗罗贝尼乌斯范数”,矩阵 L 2 L2 L2范数听起来更自然,但鉴于一些大家无须知道的特殊原因,按照惯例,我们称之为**“弗罗贝尼乌斯范数”,它表示一个矩阵中所有元素的平方和**。
该如何使用该范数实现梯度下降呢?
用backprop计算出 d W dW dW的值,backprop会给出 J J J对 W W W的偏导数,实际上是 W [ l ] W^{[l]} W[l],把 W [ l ] W^{[l]} W[l]替换为 W [ l ] W^{[l]} W[l]减去学习率乘以 d W dW dW
这就是之前我们额外增加的正则化项,既然已经增加了这个正则项,现在我们要做的就是给 d W dW dW加上这一项 λ m W l \frac{\lambda}{m}W^{l} mλWl,然后计算这个更新项,使用新定义的 d W [ l ] dW^{[l]} dW[l],它的定义含有相关参数代价函数导数和,以及最后添加的额外正则项,这也是 L 2 L2 L2正则化有时被称为“权重衰减”的原因
我们用 d W [ l ] dW^{[l]} dW[l]的定义替换此处的 d W [ l ] dW^{[l]} dW[l],可以看到, W [ l ] W^{[l]} W[l]的定义被更新为 W [ l ] W^{[l]} W[l]减去学习率 α \alpha α乘以backprop 再加上 λ m W l \frac{\lambda}{m}W^{l} mλWl
该正则项说明,不论 W [ l ] W^{[l]} W[l]是什么,我们都试图让它变得更小,实际上,相当于我们给矩阵W乘以 ( 1 − α λ m ) (1-\alpha\frac{\lambda}{m}) (1−αmλ)倍的权重,矩阵 W W W减去 α λ m \alpha\frac{\lambda}{m} αmλ倍的它,该系数小于1,因此 L 2 L2 L2范数正则化也被称为“权重衰减”,因为它就像一般的梯度下降, W W W被更新为少了 α \alpha α乘以backprop输出的最初梯度值,同时 W W W也乘以了这个系数,这个系数小于1,因此 L 2 L2 L2正则化也被称为“权重衰减”。
为什么正则化有利于预防过拟合呢?
直观理解就是 λ \lambda λ增加到足够大, W W W会接近于0,实际上是不会发生这种情况的,我们尝试消除或至少减少许多隐藏单元的影响,最终这个网络会变得更简单,这个神经网络越来越接近逻辑回归,我们直觉上认为大量隐藏单元被完全消除了,其实不然,实际上是该神经网络的所有隐藏单元依然存在,但是它们的影响变得更小了。神经网络变得更简单了,貌似这样更不容易发生过拟合,因此我不确定这个直觉经验是否有用,不过在编程中执行正则化时,你实际看到一些方差减少的结果。
dropout正则化(Dropout Regularization)
dropout(随机失活)正则化
假设你在训练上图这样的神经网络,它存在过拟合,这就是dropout所要处理的,我们复制这个神经网络,dropout会遍历网络的每一层,并设置消除神经网络中节点的概率。假设网络中的每一层,每个节点都以抛硬币的方式设置概率,每个节点得以保留和消除的概率都是0.5,设置完节点概率,我们会消除一些节点,然后删除掉从该节点进出的连线,最后得到一个节点更少,规模更小的网络,然后用backprop方法进行训练
在训练阶段如何实施dropout?
inverted dropout(反向随机失活)
这是最常用的方法
我们用一个三层( l = 3 l=3 l=3)网络来举例说明如何在某一层中实施dropout
首先要定义向量 d d d, d [ 3 ] d^{[3]} d[3]表示一个三层的dropout向量:
d3 = np.random.rand(a3.shape[0],a3.shape[1])
然后看它是否小于某数,我们称之为keep-prob,keep-prob是一个具体数字,上个示例中它是0.5,而本例中它是0.8,它表示保留某个隐藏单元的概率,此处keep-prob等于0.8,它意味着消除任意一个隐藏单元的概率是0.2,它的作用就是生成随机矩阵,如果对 a [ 3 ] a^{[3]} a[3]进行因子分解,效果也是一样的。 d [ 3 ] d^{[3]} d[3]是一个矩阵,每个样本和每个隐藏单元,其中 d [ 3 ] d^{[3]} d[3]中的对应值为1的概率都是0.8,对应为0的概率是0.2,随机数字小于0.8。它等于1的概率是0.8,等于0的概率是0.2
接下来要做的就是从第三层中获取激活函数,这里我们叫它 a [ 3 ] a^{[3]} a[3], a [ 3 ] a^{[3]} a[3]含有要计算的激活函数, a [ 3 ] a^{[3]} a[3]等于上面的 a [ 3 ] a^{[3]} a[3]乘以 d [ 3 ] d^{[3]} d[3],a3 =np.multiply(a3,d3),这里是元素相乘,也可写为 a [ 3 ] ∗ = d [ 3 ] a^{[3]}*=d^{[3]} a[3]∗=d[3],它的作用就是让 d [ 3 ] d^{[3]} d[3]中所有等于0的元素(输出),而各个元素等于0的概率只有20%,乘法运算最终把中相应元素输出,即让 d [ 3 ] d^{[3]} d[3]中0元素与 a [ 3 ] a^{[3]} a[3]中相对元素归零
如果用python实现该算法的话, d [ 3 ] d^{[3]} d[3]则是一个布尔型数组,值为true和false,而不是1和0,乘法运算依然有效,python会把true和false翻译为1和0
最后,我们向外扩展 a [ 3 ] a^{[3]} a[3],用它除以0.8,或者除以keep-prob参数
 它的功能是,不论keep-prop的值是多少0.8,0.9甚至是1,如果keep-prop设置为1,那么就不存在dropout,因为它会保留所有节点。反向随机失活(inverted dropout)方法通过除以keep-prob,确保 a [ 3 ] a^{[3]} a[3]的期望值不变。
它的功能是,不论keep-prop的值是多少0.8,0.9甚至是1,如果keep-prop设置为1,那么就不存在dropout,因为它会保留所有节点。反向随机失活(inverted dropout)方法通过除以keep-prob,确保 a [ 3 ] a^{[3]} a[3]的期望值不变。
如何在测试阶段训练算法
在测试阶段,我们已经给出了 x x x,或是想预测的变量,用的是标准计数法。我用 a [ 0 ] a^{[0]} a[0],第0层的激活函数标注为测试样本 x x x,我们在测试阶段不使用dropout函数,尤其是像下列情况:
因为在测试阶段进行预测时,我们不期望输出结果是随机的,如果测试阶段应用dropout函数,预测会受到干扰。理论上,你只需要多次运行预测处理过程,每一次,不同的隐藏单元会被随机归零,预测处理遍历它们,但计算效率低,得出的结果也几乎相同,与这个不同程序产生的结果极为相似
理解dropout
-
dropout的功能类似于 L 2 L2 L2正则化,与 L 2 L2 L2正则化不同的是应用方式不同,dropout也会有所不同,甚至更适用于不同的输入范围
-
层的keep-prob可以不同
如果你担心某些层比其它层更容易发生过拟合,可以把某些层的keep-prob值设置得比其它层更低,缺点是为了使用交叉验证,你要搜索更多的超级参数,另一种方案是在一些层上应用dropout,而有些层不用dropout,应用dropout的层只含有一个超级参数,就是keep-prob。
dropout一大缺点就是代价函数 J J J不再被明确定义,每次迭代,都会随机移除一些节点,如果再三检查梯度下降的性能,实际上是很难进行复查的。定义明确的代价函数 J J J每次迭代后都会下降,因为我们所优化的代价函数 J J J实际上并没有明确定义,或者说在某种程度上很难计算,所以我们失去了调试工具来绘制这样的图片。我通常会关闭dropout函数,将keep-prob的值设为1,运行代码,确保 J J J函数单调递减。然后打开dropout函数,希望在dropout过程中,代码并未引入bug。我觉得你也可以尝试其它方法,虽然我们并没有关于这些方法性能的数据统计,但你可以把它们与dropout方法一起使用。
其他正则化方法
除了 L 2 L2 L2正则化和随机失活(dropout)正则化,还有几种方法可以减少神经网络中的过拟合:
数据扩增
数据扩增可作为正则化方法使用,实际功能上也与正则化相似。
early stopping
还有另外一种常用的方法叫作early stopping,运行梯度下降时,我们可以绘制训练误差,或只绘制代价函数 J J J的优化过程,在训练集上用0-1记录分类误差次数。呈单调下降趋势,如图。
 通过early stopping,我们不但可以绘制上面这些内容,还可以绘制验证集误差,它可以是验证集上的分类误差,或验证集上的代价函数,逻辑损失和对数损失等,你会发现,验证集误差通常会先呈下降趋势,然后在某个节点处开始上升,early stopping的作用是,你会说,神经网络已经在这个迭代过程中表现得很好了,我们在此停止训练吧,得到验证集误差,它是怎么发挥作用的?
通过early stopping,我们不但可以绘制上面这些内容,还可以绘制验证集误差,它可以是验证集上的分类误差,或验证集上的代价函数,逻辑损失和对数损失等,你会发现,验证集误差通常会先呈下降趋势,然后在某个节点处开始上升,early stopping的作用是,你会说,神经网络已经在这个迭代过程中表现得很好了,我们在此停止训练吧,得到验证集误差,它是怎么发挥作用的?
当你还未在神经网络上运行太多迭代过程的时候,参数 w w w接近0,因为随机初始化值时,它的值可能都是较小的随机值,所以在你长期训练神经网络之前 w w w依然很小,在迭代过程和训练过程中 w w w的值会变得越来越大,比如在这儿,神经网络中参数 w w w的值已经非常大了,所以early stopping要做就是在中间点停止迭代过程,我们得到一个 w w w值中等大小的弗罗贝尼乌斯范数,与 L 2 L2 L2正则化相似,选择参数w范数较小的神经网络,但愿你的神经网络过度拟合不严重。
术语early stopping代表提早停止训练神经网络,训练神经网络时,我有时会用到early stopping,但是它也有一个缺点,我们来了解一下
在机器学习中,超级参数激增,选出可行的算法也变得越来越复杂。我发现,如果我们用一组工具优化代价函数 J J J,机器学习就会变得更简单,在重点优化代价函数 J J J时,你只需要留意 w w w和 b b b, J ( w , b ) J(w,b) J(w,b)的值越小越好,你只需要想办法减小这个值,其它的不用关注。然后,预防过拟合还有其他任务,换句话说就是减少方差,这一步我们用另外一套工具来实现,这个原理有时被称为**“正交化”**。思路就是在一个时间做一个任务,后面课上我会具体介绍正交化,如果你还不了解这个概念,不用担心。
但对我来说early stopping的主要缺点就是你不能独立地处理这两个问题,因为提早停止梯度下降,也就是停止了优化代价函数 J J J,因为现在你不再尝试降低代价函数 J J J,所以代价函数的值可能不够小,同时你又希望不出现过拟合,你没有采取不同的方式来解决这两个问题,而是用一种方法同时解决两个问题,这样做的结果是我要考虑的东西变得更复杂。
如果不用early stopping,另一种方法就是 L 2 L2 L2正则化,训练神经网络的时间就可能很长。我发现,这导致超级参数搜索空间更容易分解,也更容易搜索,但是缺点在于,你必须尝试很多正则化参数 λ \lambda λ的值,这也导致搜索大量 λ \lambda λ值的计算代价太高。
Early stopping的优点是,只运行一次梯度下降,你可以找出 w w w的较小值,中间值和较大值,而无需尝试正则化超级参数 λ \lambda λ的很多值。
吴恩达老师个人更倾向于使用 L 2 L2 L2正则化,尝试许多不同的 λ \lambda λ值,假设你可以负担大量计算的代价。
归一化输入
训练神经网络,其中一个加速训练的方法就是归一化输入。假设一个训练集有两个特征,输入特征为2维,归一化需要两个步骤:
- 零均值
- 归一化方差;
 提示一下,如果你用它来调整训练数据,那么用相同的 μ \mu μ和 σ 2 \sigma^{2} σ2 来归一化测试集。我们希望不论是训练数据还是测试数据,都是通过相同 μ \mu μ和 σ 2 \sigma^{2} σ2 定义的相同数据转换,其中 μ \mu μ和 σ 2 \sigma^{2} σ2 是由训练集数据计算得来的
提示一下,如果你用它来调整训练数据,那么用相同的 μ \mu μ和 σ 2 \sigma^{2} σ2 来归一化测试集。我们希望不论是训练数据还是测试数据,都是通过相同 μ \mu μ和 σ 2 \sigma^{2} σ2 定义的相同数据转换,其中 μ \mu μ和 σ 2 \sigma^{2} σ2 是由训练集数据计算得来的
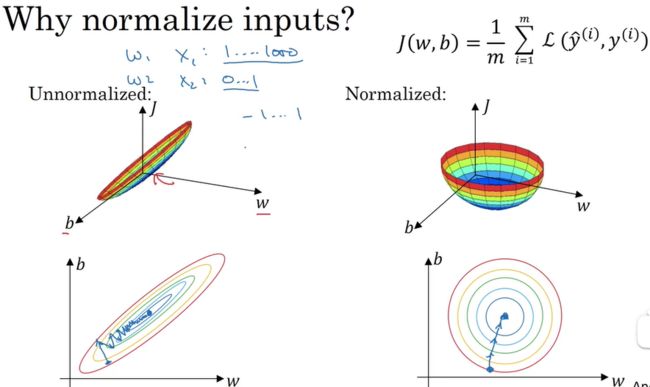
为什么要归一化输入?
当它们在非常不同的取值范围内,如其中一个从1到1000,另一个从0到1,这对优化算法非常不利。但是仅将它们设置为均化零值,假设方差为1,就像上一张幻灯片里设定的那样,确保所有特征都在相似范围内,通常可以帮助学习算法运行得更快。
所以如果输入特征处于不同范围内,可能有些特征值从0到1,有些从1到1000,那么归一化特征值就非常重要了。如果特征值处于相似范围内,那么归一化就不是很重要了。执行这类归一化并不会产生什么危害,我通常会做归一化处理,虽然我不确定它能否提高训练或算法速度。
梯度消失/梯度爆炸
训练神经网络,尤其是深度神经所面临的一个问题就是梯度消失或梯度爆炸,也就是你训练神经网络的时候,导数或坡度有时会变得非常大,或者非常小,甚至于以指数方式变小,这加大了训练的难度。
总结一下,我们讲了深度神经网络是如何产生梯度消失或爆炸问题的,实际上,在很长一段时间内,它曾是训练深度神经网络的阻力,虽然有一个不能彻底解决此问题的解决方案,但是已在如何选择初始化权重问题上提供了很多帮助。
神经网络的权重初始化
我们要为神经网络更谨慎地选择随机初始化参数
以单个神经元为例,单个神经元可能有4个输入特征,从 x 1 x_{1} x1到 x 4 x_{4} x4,经过 a = g ( z ) a=g(z) a=g(z)处理,最终得到 y ^ \widehat{y} y ,稍后讲深度网络时,这些输入表示为 a [ l ] a^{[l]} a[l],暂时我们用 x x x表示
z = w 1 x 1 + w 2 x 2 + . . . + w n x n , b = 0 z=w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n},b=0 z=w1x1+w2x2+...+wnxn,b=0,暂时忽略 b b b,为了预防 z z z值过大或过小,你可以看到 n n n越大,你希望 w i w_{i} wi越小,因为 z z z是 w i x i w_{i}x_{i} wixi的和,如果你把很多此类项相加,希望每项值更小,最合理的方法就是设置 w i = 1 n w_{i}=\frac{1}{n} wi=n1, n n n表示神经元的输入特征数量,实际上,你要做的就是设置某层权重矩阵** w [ l ] = n p . r a n d o m . r a n d n ( s h a p e ) ∗ n p . s q r t ( 1 n [ l − 1 ] ) w^{[l]}=np.random.randn(shape)*np.sqrt(\frac{1}{n^{[l-1]}}) w[l]=np.random.randn(shape)∗np.sqrt(n[l−1]1)**
结果,如果你是用的是Relu激活函数,而不是 1 n \frac{1}{n} n1,方差设置为 2 n \frac{2}{n} n2,效果会更好。
如tanh激活函数,有篇论文提到,常量1比常量2的效率更高,对于tanh函数来说,它是 1 n [ l − 1 ] \sqrt{\frac{1}{n^{[l-1]}}} n[l−1]1,这里平方根的作用与这个公式作用相同( n p . s q r t ( 1 n [ l − 1 ] ) np.sqrt(\frac{1}{n^{[l-1]}}) np.sqrt(n[l−1]1)),它适用于tanh激活函数,被称为Xavier初始化
如果你想用Relu激活函数,也就是最常用的激活函数,我会用这个公式** n p . s q r t ( 2 n [ l − 1 ] ) np.sqrt(\frac{2}{n^{[l-1]}}) np.sqrt(n[l−1]2),如果使用tanh函数,可以用公式 1 n [ l − 1 ] \sqrt\frac{1}{n^{[l-1]}} n[l−1]1**,有些作者也会使用这个函数。
梯度的数值逼近
在实施backprop时,有一个测试叫做梯度检验,它的作用是确保backprop正确实施。因为有时候,你虽然写下了这些方程式,却不能100%确定,执行backprop的所有细节都是正确的。为了逐渐实现梯度检验,我们首先说说如何计算梯度的数值逼近,下节课,我们将讨论如何在backprop中执行梯度检验,以确保backprop正确实施。
所以在执行梯度检验时,我们使用双边误差,即 f ( θ + ε ) − f ( θ − ε ) 2 ε \frac{f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon} 2εf(θ+ε)−f(θ−ε),而不使用单边公差,因为它不够准确
梯度检验
梯度检验帮我们节省了很多时间,也多次帮我发现backprop实施过程中的bug,接下来 ,我们看看如何利用它来调试或检验backprop的实施是否正确。
这就是实施梯度检验的过程,英语里通常简称为“grad check”,首先,我们要清楚 J J J是超参数 θ \theta θ的一个函数,你也可以将J函数展开为 J ( θ 1 , θ 2 , θ 3 , . . . ) J(\theta_{1},\theta_{2},\theta_{3},...) J(θ1,θ2,θ3,...),不论超级参数向量 θ \theta θ的维度是多少,为了实施梯度检验,你要做的就是循环执行,从而对每个 i i i也就是对每个 θ \theta θ组成元素计算 d θ a p p r o x [ i ] d\theta_{approx}[i] dθapprox[i]的值,我使用双边误差,也就是
d θ a p p r o x [ i ] = J ( θ 1 , θ 2 , . . . , θ i + ε , . . . ) − J ( θ 1 , θ 2 , . . . , θ i − ε , . . . ) 2 ε d\theta_{approx}[i]=\frac{J(\theta_{1},\theta_{2},...,\theta{i}+\varepsilon,...)-J(\theta_{1},\theta_{2},...,\theta_{i}-\varepsilon,...)}{2\varepsilon} dθapprox[i]=2εJ(θ1,θ2,...,θi+ε,...)−J(θ1,θ2,...,θi−ε,...)
只对 θ i \theta_{i} θi增加 ε \varepsilon ε,其它项保持不变,因为我们使用的是双边误差,对另一边做同样的操作,只不过是减去,其它项全都保持不变。
具体来说,如何定义两个向量是否真的接近彼此?我一般做下列运算,计算这两个向量的距离, d θ a p p r o x [ i ] − d θ [ i ] d\theta_{approx}[i]-d\theta[i] dθapprox[i]−dθ[i]的欧几里得范数,注意这里( ∣ ∣ d θ a p p r o x − d θ ∣ ∣ 2 ||d\theta_{approx}-d\theta||_{2} ∣∣dθapprox−dθ∣∣2)没有平方,它是误差平方之和,然后求平方根,得到欧式距离,然后用向量长度归一化,使用向量长度的欧几里得范数。分母只是用于预防这些向量太小或太大,分母使得这个方程式变成比率
,我们实际执行这个方程式, ε \varepsilon ε可能为 1 0 − 7 10^{-7} 10−7,使用这个取值范围内的,如果你发现计算方程式得到的值为 1 0 − 7 10^{-7} 10−7或更小,这就很好,这就意味着导数逼近很有可能是正确的,它的值非常小。
如果它的值在 1 0 − 5 10^{-5} 10−5范围内,我就要小心了,也许这个值没问题,但我会再次检查这个向量的所有项,确保没有一项误差过大,可能这里有bug。
如果左边这个方程式结果是 1 0 − 3 10^{-3} 10−3,我就会担心是否存在bug,计算结果应该比 1 0 − 3 10^{-3} 10−3小很多,如果比 1 0 − 3 10^{-3} 10−3大很多,我就会很担心,担心是否存在bug。这时应该仔细检查所有 θ \theta θ项,看是否有一个具体的 i i i值,使得 d θ a p p r o x [ i ] 与 d θ [ i ] d\theta_{approx}[i]与d\theta[i] dθapprox[i]与dθ[i]大不相同,并用它来追踪一些求导计算是否正确,经过一些调试,最终结果会是这种非常小的值( 1 0 − 7 10^{-7} 10−7),那么,你的实施可能是正确的。
在实施神经网络时,我经常需要执行foreprop和backprop,然后我可能发现这个梯度检验有一个相对较大的值,我会怀疑存在bug,然后开始调试,调试,调试,调试一段时间后,我得到一个很小的梯度检验值,现在我可以很自信的说,神经网络实施是正确的。
梯度检验应用的注意事项
分享一些关于如何在神经网络实施梯度检验的实用技巧和注意事项
例题
你正在为苹果,香蕉和橘子制作分类器。 假设您的分类器在训练集上有0.5%的错误,以及开发集上有7%的错误。 以下哪项尝试是有希望改善你的分类器的分类效果的?
- 增大正则化参数 λ \lambda λ 2. 获取更多训练数据
【增加 λ \lambda λ,权重衰减更剧烈,如果 λ \lambda λ增加到足够大, W W W会接近于0,实际上是不会发生这种情况的,我们尝试消除或至少减少许多隐藏单元的影响,最终这个网络会变得更简单,这个神经网络越来越接近逻辑回归,神经网络变得更简单了,貌似这样更不容易发生过拟合】
优化算法
优化算法能够帮助你快速训练模型
我们可以利用一个巨大的数据集来训练神经网络,而在巨大的数据集基础上进行训练速度很慢。使用快速的优化算法,使用好用的优化算法能够大大提高训练的效率
Mini-batch 梯度下降
使用 X { t } , Y { t } X^{\{t\}},Y^{\{t\}} X{t},Y{t}来表示第 t t t个mini-batch
矢量化不适用于同时计算多个mini-batch
理解mini-batch梯度下降法
没有每次迭代都下降是不要紧的,但走势应该向下,噪声产生的原因在于也许 X { 1 } X^{\{1\}} X{1}和 Y { 1 } Y^{\{1\}} Y{1}是比较容易计算的mini-batch,因此成本会低一些。不过也许出于偶然, X { 2 } X^{\{2\}} X{2}和 Y { 2 } Y^{\{2\}} Y{2}是比较难运算的mini-batch,或许你需要一些残缺的样本,这样一来,成本会更高一些,所以才会出现这些摆动,因为你是在运行mini-batch梯度下降法作出成本函数图
首先,如果训练集较小,直接使用batch梯度下降法,样本集较小就没必要使用mini-batch梯度下降法,你可以快速处理整个训练集,所以使用batch梯度下降法也很好,这里的少是说小于2000个样本,这样比较适合使用batch梯度下降法。不然,样本数目较大的话,一般的mini-batch大小为64到512,考虑到电脑内存设置和使用的方式,如果mini-batch大小是2的 n n n次方,代码会运行地快一些,64就是2的6次方,以此类推,128是2的7次方,256是2的8次方,512是2的9次方。所以我经常把mini-batch大小设成2的次方。在上一个视频里,我的mini-batch大小设为了1000,建议你可以试一下1024,也就是2的10次方。也有mini-batch的大小为1024,不过比较少见,64到512的mini-batch比较常见。
最后需要注意的是在你的mini-batch中,要确保 X { t } X^{\{t\}} X{t}和 Y { t } Y^{\{t\}} Y{t}要符合CPU/GPU内存,取决于你的应用方向以及训练集的大小。如果你处理的mini-batch和CPU/GPU内存不相符,不管你用什么方法处理数据,你会注意到算法的表现急转直下变得惨不忍睹,所以我希望你对一般人们使用的mini-batch大小有一个直观了解。事实上mini-batch大小是另一个重要的变量,你需要做一个快速尝试,才能找到能够最有效地减少成本函数的那个,我一般会尝试几个不同的值,几个不同的2次方,然后看能否找到一个让梯度下降优化算法最高效的大小。希望这些能够指导你如何开始找到这一数值。
不过还有个更高效的算法,比梯度下降法和mini-batch梯度下降法都要高效的多,我们在接下来的视频中将为大家一一讲解。
指数加权平均数
我想向你展示几个优化算法,它们比梯度下降法快,要理解这些算法,你需要用到指数加权平均,在统计中也叫做指数加权移动平均,我们首先讲这个,然后再来讲更复杂的优化算法。
所以指数加权平均数经常被使用,再说一次,它在统计学中被称为指数加权移动平均值,我们就简称为指数加权平均数。通过调整这个参数( β \beta β),或者说后面的算法学习,你会发现这是一个很重要的参数,可以取得稍微不同的效果,往往中间有某个值效果最好, β \beta β为中间值时得到的红色曲线,比起绿线和黄线更好地平均了温度。
理解指数加权平均数
指数加权平均数,这是几个优化算法中的关键一环,而这几个优化算法能帮助你训练神经网络。本视频中,我希望进一步探讨算法的本质作用
回忆一下这个计算指数加权平均数的关键方程:
v t = β v t − 1 + ( 1 − β ) θ t v_{t}=\beta v_{t-1}+(1-\beta)\theta_{t} vt=βvt−1+(1−β)θt
我们进一步地分析,来理解如何计算出每日温度的平均值
最后讲讲如何在实际中执行
指数加权平均数公式的好处之一在于,它占用极少内存,电脑内存中只占用一行数字而已,然后把最新数据代入公式,不断覆盖就可以了,正因为这个原因,其效率,它基本上只占用一行代码,计算指数加权平均数也只占用单行数字的存储和内存,当然它并不是最好的,也不是最精准的计算平均数的方法。如果你要计算移动窗,你直接算出过去10天的总和,过去50天的总和,除以10和50就好,如此往往会得到更好的估测。但缺点是,如果保存所有最近的温度数据,和过去10天的总和,必须占用更多的内存,执行更加复杂,计算成本也更加高昂。
所以在接下来的视频中,我们会计算多个变量的平均值,从计算和内存效率来说,这是一个有效的方法,所以在机器学习中会经常使用,更不用说只要一行代码,这也是一个优势。
指数加权平均的偏差修正
学过了如何计算指数加权平均数,有一个技术名词叫做偏差修正,可以让平均数运算更加准确,来看看它是怎么运行的。
在上一个视频中,这个(红色)曲线对应 β \beta β的值为0.9,这个(绿色)曲线对应的 β \beta β=0.98,如果你执行写在这里的公式,在 β \beta β等于0.98的时候,得到的并不是绿色曲线,而是紫色曲线,你可以注意到紫色曲线的起点较低,我们来看看怎么处理。
有个办法可以修改这一估测,让估测变得更好,更准确,特别是在估测初期,也就是不用 v t v_{t} vt,而是用 v t 1 − β t \frac{v_{t}}{1-\beta^{t}} 1−βtvt, t t t就是现在的天数。
你会发现随着 t t t增加, β t \beta^{t} βt接近于0,所以当 t t t很大的时候,偏差修正几乎没有作用,因此当较大的时候,紫线基本和绿线重合了。不过在开始学习阶段,你才开始预测热身练习,偏差修正可以帮助你更好预测温度,偏差修正可以帮助你使结果从紫线变成绿线。
在机器学习中,在计算指数加权平均数的大部分时候,大家不在乎执行偏差修正,因为大部分人宁愿熬过初始时期,拿到具有偏差的估测,然后继续计算下去。如果你关心初始时期的偏差,在刚开始计算指数加权移动平均数的时候,偏差修正能帮助你在早期获取更好的估测。
动量梯度下降法
还有一种算法叫做Momentum,或者叫做动量梯度下降法,运行速度几乎总是快于标准的梯度下降算法,简而言之,基本的想法就是计算梯度的指数加权平均数,并利用该梯度更新你的权重
β \beta β最常用的值是0.9,我们之前平均了过去十天的温度,所以现在平均了前十次迭代的梯度。实际上 β \beta β为0.9时,效果不错,你可以尝试不同的值,可以做一些超参数的研究,不过0.9是很棒的鲁棒数。
RMSprop
你们知道了动量(Momentum)可以加快梯度下降,还有一个叫做RMSprop的算法,全称是root mean square prop算法,它也可以加速梯度下降,我们来看看它是如何运作的!
下一个视频中,我们会将RMSprop和Momentum结合起来,我们在Momentum中采用超参数 β \beta β,为了避免混淆,我们现在不用 β \beta β,而采用超参数 β 2 \beta_{2} β2以保证在Momentum和RMSprop中采用同一超参数。要确保你的算法不会除以0,如果 S d W S_{dW} SdW的平方根趋近于0怎么办?得到的答案就非常大,为了确保数值稳定,在实际操练的时候,你要在分母上加上一个很小很小的 ε {\varepsilon} ε, ε \varepsilon ε是多少没关系, 1 0 − 8 10^{-8} 10−8是个不错的选择,这只是保证数值能稳定一些,无论什么原因,你都不会除以一个很小很小的数。
所以RMSprop跟Momentum有很相似的一点,可以消除梯度下降中的摆动,包括mini-batch梯度下降,并允许你使用一个更大的学习率 α \alpha α,从而加快你的算法学习速度
我们讲过了Momentum,我们讲了RMSprop,如果二者结合起来,你会得到一个更好的优化算法
Adam优化算法
很多人都觉得动量(Momentum)梯度下降法很好用,很难再想出更好的优化算法。所以RMSprop以及Adam优化算法(Adam优化算法也是本视频的内容),就是少有的经受住人们考验的两种算法,已被证明适用于不同的深度学习结构,这个算法我会毫不犹豫地推荐给你,因为很多人都试过,并且用它很好地解决了许多问题。
相当于Momentum更新了超参数 β 1 \beta_{1} β1,RMSprop更新了超参数 β 2 \beta_{2} β2。一般使用Adam算法的时候,要计算偏差修正
所以Adam算法结合了Momentum和RMSprop梯度下降法,并且是一种极其常用的学习算法,被证明能有效适用于不同神经网络,适用于广泛的结构
本算法中有很多超参数,超参数学习率 α \alpha α很重要,也经常需要调试,你可以尝试一系列值,然后看哪个有效。而 β 1 , β 2 , ε \beta_{1},\beta_{2},{\varepsilon} β1,β2,ε使用常用的缺省值即可
学习率衰减
加快学习算法的一个办法就是随时间慢慢减少学习率,我们将之称为学习率衰减,我们来看看如何做到,首先通过一个例子看看,为什么要计算学习率衰减。
所以慢慢减少 α \alpha α的本质在于,在学习初期,你能承受较大的步伐,但当开始收敛的时候,小一些的学习率能让你步伐小一些。
将数据集拆分成不同的mini-batch,第一次遍历训练集叫做第一代。第二次就是第二代,依此类推,你可以将学习率设为 α = 1 1 + d e c a y r a t e ∗ e p o c h − n u m a 0 \alpha=\frac{1}{1+decayrate*epoch-num}a_{0} α=1+decayrate∗epoch−num1a0(decay-rate称为衰减率,epoch-num为代数, α 0 \alpha_{0} α0为初始学习率),注意这个衰减率是另一个你需要调整的超参数。
如果你想用学习率衰减,要做的是要去尝试不同的值,包括超参数 α 0 \alpha_{0} α0,以及超参数衰退率,找到合适的值,除了这个学习率衰减的公式,人们还会用其它的公式。
比如,这个叫做指数衰减,其中 α \alpha α相当于一个小于1的值,如 α = 0.9 5 e p o c h − n u m a 0 \alpha=0.95^{epoch-num}a_{0} α=0.95epoch−numa0,所以你的学习率呈指数下降。
人们用到的其它公式有 α = k e p o c h − n u m a 0 \alpha=\frac{k}{\sqrt{epoch-num}}a_{0} α=epoch−numka0或者 α = k t a 0 \alpha=\frac{k}{\sqrt{t}}a_{0} α=tka0( t t t为mini-batch的数字)
有时人们也会用一个离散下降的学习率,也就是某个步骤有某个学习率,一会之后,学习率减少了一半,一会儿减少一半,一会儿又一半,这就是离散下降(discrete stair cease)的意思。
到现在,我们讲了一些公式,看学习率 α \alpha α究竟如何随时间变化。人们有时候还会做一件事,手动衰减。如果你一次只训练一个模型,如果你要花上数小时或数天来训练,有些人的确会这么做,看看自己的模型训练,耗上数日,然后他们觉得,学习速率变慢了,我把 α \alpha α调小一点。手动控制 α \alpha α当然有用,时复一时,日复一日地手动调整 α \alpha α,只有模型数量小的时候有用,但有时候人们也会这么做。
局部最优的问题
在深度学习研究早期,人们总是担心优化算法会困在极差的局部最优,不过随着深度学习理论不断发展,我们对局部最优的理解也发生了改变。
这是曾经人们在想到局部最优时脑海里会出现的图。如果你要作图计算一个数字,比如说这两个维度,就容易出现有多个不同局部最优的图,而这些低维的图曾经影响了我们的理解,但是这些理解并不正确。事实上,如果你要创建一个神经网络,通常梯度为零的点并不是这个图中的局部最优点,实际上成本函数的零梯度点,通常是鞍点。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sanF2n72-1616411632526)(C:/Users/Administrator/AppData/Roaming/Typora/typora-user-images/image-20210310211227440.png)]
但是一个具有高维度空间的函数,如果梯度为0,那么在每个方向,它可能是凸函数,也可能是凹函数。如果你在2万维空间中,那么想要得到局部最优,所有的2万个方向都需要是这样,但发生的机率也许很小,也许是 2 − 20000 2^{-20000} 2−20000,你更有可能遇到有些方向的曲线会这样向上弯曲,另一些方向曲线向下弯,而不是所有的都向上弯曲,因此在高维度空间,你更可能碰到鞍点。就像下面的这种:
而不会碰到局部最优。
如果局部最优不是问题,那么问题是什么?结果是平稳段会减缓学习,平稳段是一块区域,其中导数长时间接近于0,如果你在此处,梯度会从曲面从从上向下下降,因为梯度等于或接近0,曲面很平坦,你得花上很长时间慢慢抵达平稳段的这个点,因为左边或右边的随机扰动,然后你的算法能够走出平稳段(红色笔)。
所以此次视频的要点是,首先,你不太可能困在极差的局部最优中,条件是你在训练较大的神经网络,存在大量参数,并且成本函数 J J J被定义在较高的维度空间。
第二点,平稳段是一个问题,这样使得学习十分缓慢,这也是像Momentum或是RMSprop,Adam这样的算法,能够加速学习算法的地方。在这些情况下,更成熟的优化算法,如Adam算法,能够加快速度,让你尽早往下走出平稳段。
python实现
#%matplotlib inline #如果你用的是Jupyter Notebook请取消注释
#pylot使用rc配置文件来自定义图形的各种默认属性,称之为rc配置或rc参数
plt.rcParams['figure.figsize'] = (7.0,4.0) #set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# 批量梯度下降(Batch Gradient Descent)
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
使用梯度下降更新参数
参数:
parameters - 字典,包含了要更新的参数:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads - 字典,包含了每一个梯度值用以更新参数
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
learning_rate - 学习率
返回值:
parameters - 字典,包含了更新后的参数
"""
L = len(parameters) // 2 #神经网络层数
#更新每个参数
for l in range(L):
parameters['W'+str(l+1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters['b'+str(l+1)] = parameters['b' + str(l + 1)] - learning_rate * grads['db' + str(l + 1)]
return parameters
# mini-batch梯度下降
#1.把训练集打乱
#2.切分
def random_mini_batches(X,Y,mini_batch_size=64,seed=0):
"""
从(X,Y)中创建一个随机的mini-batch列表
参数:
X - 输入数据,维度为(输入节点数量,样本的数量)
Y - 对应的是X的标签,【1 | 0】(蓝|红),维度为(1,样本的数量)
mini_batch_size - 每个mini-batch的样本数量
返回:
mini-bacthes - 一个同步列表,维度为(mini_batch_X,mini_batch_Y)
"""
np.random.seed(seed) #指定随机种子
m = X.shape[1]
mini_batches = []
#第一步:打乱顺序
permutation = list(np.random.permutation(m))#它会返回一个长度为m的随机数组,且里面的数是0到m-1
shuffled_X = X[:,permutation] #将每一列的数据按permutation的顺序来重新排列
shuffled_Y = Y[:,permutation].reshape((1,m))
#第二步:分割
num_complete_minibatches = math.floor(m / mini_batch_size)
# 把你的训练集分割成多少份,请注意,如果值是99.99,那么返回值是99,剩下的0.99会被舍弃
for k in range(0,num_complete_minibatches):
mini_batch_X = shuffled_X[:,k * mini_batch_size:(k+1)*mini_batch_size]
mini_batch_Y = shuffled_Y[:,k * mini_batch_size:(k+1)*mini_batch_size]
mini_batch = (mini_batch_X,mini_batch_Y)
mini_batches.append(mini_batch)
if m % mini_batch_size != 0:
mini_batch_X = shuffled_X[:,mini_batch_size*num_complete_minibatches:]
mini_batch_Y = shuffled_Y[:,mini_batch_size*num_complete_minibatches:]
mini_batch = (mini_batch_X,mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
# 包含动量的梯度下降
def initialize_velocity(parameters):
"""
初始化速度,velocity是一个字典:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values:与相应的梯度/参数维度相同的值为零的矩阵。
参数:
parameters - 一个字典,包含了以下参数:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
返回:
v - 一个字典变量,包含了以下参数:
v["dW" + str(l)] = dWl的速度
v["db" + str(l)] = dbl的速度
"""
L = len(parameters) // 2
v = {}
for l in range(L):
v["dW" + str(l+1)] = np.zeros_like(parameters["W" + str(l + 1)])
v["db" + str(l+1)] = np.zeros_like(parameters["b" + str(l + 1)])
return v
def update_parameters_with_momentun(parameters,grads,v,beta,learning_rate):
"""
使用动量更新参数
参数:
parameters - 一个字典类型的变量,包含了以下字段:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
grads - 一个包含梯度值的字典变量,具有以下字段:
grads["dW" + str(l)] = dWl
grads["db" + str(l)] = dbl
v - 包含当前速度的字典变量,具有以下字段:
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
beta - 超参数,动量,实数
learning_rate - 学习率,实数
返回:
parameters - 更新后的参数字典
v - 包含了更新后的速度变量
"""
L = len(parameters) // 2
for l in range(L):
# 计算速度
v["dW"+str(l+1)] = beta * v["dW"+str(l+1)] +(1-beta) *grads["dW"+str(l+1)]
v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads["db" + str(l + 1)]
# 更新参数
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]
return parameters,v
#Adam算法
#1、计算以前的梯度的指数加权平均值,v
#2、计算以前梯度的平均的指数加权平均值,s
def initialize_adam(parameters):
"""
初始化v和s,它们都是字典类型的变量,都包含了以下字段:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values:与对应的梯度/参数相同维度的值为零的numpy矩阵
参数:
parameters - 包含了以下参数的字典变量:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
返回:
v - 包含梯度的指数加权平均值,字段如下:
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s - 包含平方梯度的指数加权平均值,字段如下:
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2
v = {}
s = {}
for l in range(L):
v["dW"+str(l+1)] = np.zeros_like(parameters["W"+str(l+1)])
v["db"+str(l+1)] = np.zeros_like(parameters["b"+str(l+1)])
s["dW"+str(l+1)] = np.zeros_like(parameters["W"+str(l+1)])
s["db"+str(l+1)] = np.zeros_like(parameters["b"+str(l+1)])
return (v,s)
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8):
"""
使用Adam更新参数
参数:
parameters - 包含了以下字段的字典:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads - 包含了梯度值的字典,有以下key值:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v - Adam的变量,第一个梯度的移动平均值,是一个字典类型的变量
s - Adam的变量,平方梯度的移动平均值,是一个字典类型的变量
t - 当前迭代的次数
learning_rate - 学习率
beta1 - 动量,超参数,用于第一阶段,使得曲线的Y值不从0开始(参见天气数据的那个图)
beta2 - RMSprop的一个参数,超参数
epsilon - 防止除零操作(分母为0)
返回:
parameters - 更新后的参数
v - 第一个梯度的移动平均值,是一个字典类型的变量
s - 平方梯度的移动平均值,是一个字典类型的变量
"""
L = len(parameters) // 2
v_corrected = {} #偏差修正后的值
s_corrected = {}
for l in range(L):
# 梯度的移动平均值,输入:"v , grads , beta1",输出:" v "
v["dW"+str(l+1)] = beta1 * v["dW"+str(l+1)] + (1-beta1) * grads["dW"+str(l+1)]
v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads["db" + str(l + 1)]
# 计算第一阶段的偏差修正后的估计值,输入"v , beta1 , t" , 输出:"v_corrected"
v_corrected["dW"+str(l+1)] = v["dW"+str(l+1)] / (1-np.power(beta1,t))
v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1, t))
# 计算平方梯度的移动平均值,输入:"s, grads , beta2",输出:"s"
s["dW"+str(l+1)] = beta2 * s["dW"+str(l+1)] + (1-beta2) * np.power(grads["dW"+str(l+1)],2)
s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.square(grads["db" + str(l + 1)])
# 计算第二阶段的偏差修正后的估计值,输入:"s , beta2 , t",输出:"s_corrected"
s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2, t))
s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2, t))
# 更新参数,输入: "parameters, learning_rate, v_corrected, s_corrected, epsilon". 输出: "parameters".
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * (
v_corrected["dW" + str(l + 1)] / np.sqrt(s_corrected["dW" + str(l + 1)] + epsilon))
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * (
v_corrected["db" + str(l + 1)] / np.sqrt(s_corrected["db" + str(l + 1)] + epsilon))
return (parameters,v,s)
超参数调试、Batch正则化和程序框架
调试处理
希望你粗略了解到哪些超参数较为重要,经常需要调试。 α \alpha α无疑是最重要的,接下来是我用橙色圈住的那些,然后是我用紫色圈住的那些,但这不是严格且快速的标准
现在,如果你尝试调整一些超参数,该如何选择调试值呢?
实践中,对于你的具体应用而言,使用随机取值而不是网格取值,这样探究了更多重要超参数的潜在值,无论结果是什么。
当你给超参数取值时,另一个惯例是采用由粗糙到精细的策略
比如在二维的那个例子中,你进行了取值,也许你会发现效果最好的某个点,也许这个点周围的其他一些点效果也很好,那在接下来要做的是放大这块小区域(小蓝色方框内),然后在其中更密集得取值或随机取值,聚集更多的资源,在这个蓝色的方格中搜索,如果你怀疑这些超参数在这个区域的最优结果,那在整个的方格中进行粗略搜索后,你会知道接下来应该聚焦到更小的方格中。在更小的方格中,你可以更密集得取点。所以这种从粗到细的搜索也经常使用。
为超参数选择合适的范围
这是在几个在你考虑范围内随机均匀取值的例子,这些取值还蛮合理的,但对某些超参数而言不适用。
看看这个例子,假设你在搜索超参数 α \alpha α(学习速率),假设你怀疑其值最小是0.0001或最大是1。如果你画一条从0.0001到1的数轴,沿其随机均匀取值,那90%的数值将会落在0.1到1之间,结果就是,在0.1到1之间,应用了90%的资源,而在0.0001到0.1之间,只有10%的搜索资源,这看上去不太对。
反而,用对数标尺搜索超参数的方式会更合理,因此这里不使用线性轴,分别依次取0.0001,0.001,0.01,0.1,1,在对数轴上均匀随机取点,这样,在0.0001到0.001之间,就会有更多的搜索资源可用,还有在0.001到0.01之间等等。
所以在Python中,你可以这样做,使r=-4*np.random.rand(),然后 α \alpha α随机取值, α = 1 0 r \alpha=10^{r} α=10r,所以第一行可以得出 r ∈ [ − 4 , 0 ] r\in[-4,0] r∈[−4,0],那么 α ∈ [ 1 0 − 4 , 1 0 0 ] \alpha\in[10^{-4},10^{0}] α∈[10−4,100],所以最左边的数字是 1 0 − 4 10^{-4} 10−4,最右边是 1 0 0 10^{0} 100。
所以总结一下,在对数坐标下取值,取最小值的对数就得到 a a a的值,取最大值的对数就得到 b b b值,所以现在你在对数轴上的 1 0 a 10^{a} 10a到 1 0 b 10^{b} 10b区间取值,在 a a a, b b b间随意均匀的选取 r r r值,将超参数设置为 1 0 r 10^{r} 10r,这就是在对数轴上取值的过程。
最后,另一个棘手的例子是给 β \beta β取值,用于计算指数的加权平均值。假设你认为 β \beta β是0.9到0.999之间的某个值,也许这就是你想搜索的范围。记住这一点,当计算指数的加权平均值时,取0.9就像在10个值中计算平均值,有点类似于计算10天的温度平均值,而取0.999就是在1000个值中取平均。
所以考虑这个问题最好的方法就是,我们要探究的是 1 − β 1-\beta 1−β,此值在0.1到0.001区间内,所以我们会给 1 − β 1-\beta 1−β取值,大概是从0.1到0.001,应用之前幻灯片中介绍的方法,这是 1 0 − 1 10^{-1} 10−1,这是 1 0 − 3 10^{-3} 10−3,值得注意的是,在之前的幻灯片里,我们把最小值写在左边,最大值写在右边,但在这里,我们颠倒了大小。这里,左边的是最大值,右边的是最小值。所以你要做的就是在 [ − 3 , − 1 ] [-3,-1] [−3,−1]里随机均匀的给r取值。你设定了 1 − β = 1 0 r 1-\beta=10^{r} 1−β=10r,所以 β = 1 − 1 0 r \beta=1-10^{r} β=1−10r,然后这就变成了在特定的选择范围内超参数随机取值。希望用这种方式得到想要的结果,你在0.9到0.99区间探究的资源,和在0.99到0.999区间探究的一样多。
![]()
希望能帮助你选择合适的标尺,来给超参数取值。如果你没有在超参数选择中作出正确的标尺决定,别担心,即使你在均匀的标尺上取值,如果数值总量较多的话,你也会得到还不错的结果,尤其是应用从粗到细的搜索方法,在之后的迭代中,你还是会聚焦到有用的超参数取值范围上。
超参数调试的实验:Pandas VS Caviar
如今的深度学习已经应用到许多不同的领域,某个应用领域的超参数设定,有可能通用于另一领域,不同的应用领域出现相互交融。比如,我曾经看到过计算机视觉领域中涌现的巧妙方法,比如说Confonets或ResNets,这我们会在后续课程中讲到。它还成功应用于语音识别,我还看到过最初起源于语音识别的想法成功应用于NLP等等。
深度学习领域中,发展很好的一点是,不同应用领域的人们会阅读越来越多其它研究领域的文章,跨领域去寻找灵感。
最后,关于如何搜索超参数的问题,我见过大概两种重要的思想流派或人们通常采用的两种重要但不同的方式
一种是你照看一个模型,通常是有庞大的数据组,但没有许多计算资源或足够的CPU和GPU的前提下,基本而言,你只可以一次负担起试验一个模型或一小批模型,在这种情况下,即使当它在试验时,你也可以逐渐改良。所以这是一个人们照料一个模型的方法,观察它的表现,耐心地调试学习率,但那通常是因为你没有足够的计算能力,不能在同一时间试验大量模型时才采取的办法。
另一种方法则是同时试验多种模型,你设置了一些超参数,尽管让它自己运行,或者是一天甚至多天,然后你会获得像这样的学习曲线,这可以是损失函数J或实验误差或损失或数据误差的损失,但都是你曲线轨迹的度量。只是最后快速选择工作效果最好的那个。
所以这两种方式的选择,是由你拥有的计算资源决定的,如果你拥有足够的计算机去平行试验许多模型,那绝对采用鱼子酱方式,尝试许多不同的超参数,看效果怎么样。但在一些应用领域,比如在线广告设置和计算机视觉应用领域,那里的数据太多了,你需要试验大量的模型,所以同时试验大量的模型是很困难的,它的确是依赖于应用的过程。但我看到那些应用熊猫方式多一些的组织,那里,你会像对婴儿一样照看一个模型,调试参数,试着让它工作运转。尽管,当然,甚至是在熊猫方式中,试验一个模型,观察它工作与否,也许第二或第三个星期后,也许我应该建立一个不同的模型(绿色曲线),像熊猫那样照料它,我猜,这样一生中可以培育几个孩子,即使它们一次只有一个孩子或孩子的数量很少。
归一化网络的激活函数
在深度学习兴起后,最重要的一个思想是它的一种算法,叫做Batch归一化,由Sergey loffe和Christian Szegedy两位研究者创造。Batch归一化会使你的参数搜索问题变得很容易,使神经网络对超参数的选择更加稳定,超参数的范围会更加庞大,工作效果也很好,也会是你的训练更加容易,甚至是深层网络。让我们来看看Batch归一化是怎么起作用的吧。
当训练一个模型,比如logistic回归时,你也许会记得,归一化输入特征可以加快学习过程。
那么更深的模型呢?归一化 a [ 2 ] a^{[2]} a[2]的平均值和方差岂不是很好?以便使 w [ 3 ] w^{[3]} w[3], b [ 3 ] b^{[3]} b[3]的训练更有效率。实践中,经常做的是归一化 z [ 2 ] z^{[2]} z[2],我推荐其为默认选择,那下面就是Batch归一化的使用方法。
隐藏层中的归一化,不想让隐藏单元总是含有平均值0和方差1,也许隐藏单元有了不同的分布会有意义
有了 γ \gamma γ和 β \beta β两个参数后,你可以确保所有的 z ( i ) z^{(i)} z(i)值可以是你想赋予的任意值,或者它的作用是保证隐藏的单元已使均值和方差标准化。那里,均值和方差由两参数控制,即 γ \gamma γ和 β \beta β,学习算法可以设置为任何值,所以它真正的作用是,使隐藏单元值的均值和方差标准化,即 z ( i ) z^{(i)} z(i)有固定的均值和方差,均值和方差可以是0和1,也可以是其它值,它是由 γ \gamma γ和 β \beta β两参数控制的。
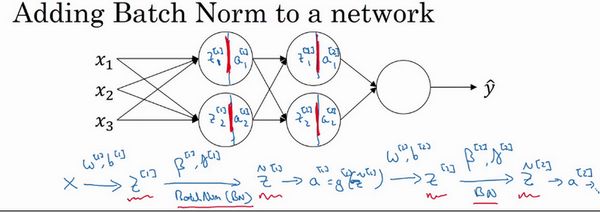
将Batch Norm拟合进神经网络
如何将Batch归一化与神经网络甚至是深度神经网络相匹配;对于神经网络许多不同层而言,又该如何使它适用
已经看到那些等式,它可以在单一隐藏层进行Batch归一化,接下来,让我们看看它是怎样在深度网络训练中拟合的吧。
每层的参数有:
即使在之前的视频中,我已经解释过Batch归一化是怎么操作的,计算均值和方差,减去均值,再除以方差,如果它们使用的是深度学习编程框架,通常你不必自己把Batch归一化步骤应用于Batch归一化层。因此,探究框架,可写成一行代码,比如说,在TensorFlow框架中,你可以用这个函数(tf.nn.batch_normalization)来实现Batch归一化,我们稍后讲解,但实践中,你不必自己操作所有这些具体的细节,但知道它是如何作用的,你可以更好的理解代码的作用。但在深度学习框架中,Batch归一化的过程,经常是类似一行代码的东西。
实践中,Batch归一化通常和训练集的mini-batch一起使用。
所以,如果你在使用Batch归一化,其实你可以消除这个参数( b [ l ] b^{[l]} b[l]),或者你也可以,暂时把它设置为0
让我们总结一下关于如何用Batch归一化来应用梯度下降法,假设你在使用mini-batch梯度下降法,你运行 t = 1 t=1 t=1到mini-batches数量的for循环,
如果你已将梯度计算如下,你就可以使用梯度下降法了,这就是我写到这里的,但也适用于有Momentum、RMSprop、Adam的梯度下降法。与其使用梯度下降法更新mini-batch,你可以使用这些其它算法来更新,我们在之前几个星期中的视频中讨论过的,也可以应用其它的一些优化算法来更新由Batch归一化添加到算法中的 β \beta β和 γ \gamma γ参数。
Batch-norm为什么奏效?
为什么Batch归一化会起作用呢?
一个原因是,你已经看到如何归一化输入特征值 x x x,使其均值为0,方差1,它又是怎样加速学习的,有一些从0到1而不是从1到1000的特征值,通过归一化所有的输入特征值 x x x,以获得类似范围的值,可以加速学习。所以Batch归一化起的作用的原因,直观的一点就是,它在做类似的工作,但不仅仅对于这里的输入值,还有隐藏单元的值,这只是Batch归一化作用的冰山一角,还有些深层的原理,它会有助于你对Batch归一化的作用有更深的理解,让我们一起来看看吧。
Batch归一化有效的第二个原因是,它可以使权重比你的网络更滞后或更深层,比如,第10层的权重更能经受得住变化,相比于神经网络中前层的权重,比如第1层,为了解释我的意思,让我们来看看这个最生动形象的例子。
也许无法期待,在左边训练得很好的模块在右边也运行的很好
所以使你数据改变分布的这个想法,有个有点怪的名字“Covariate shift”,想法是这样的,如果你已经学习了到 的映射,如果 的分布改变了,那么你可能需要重新训练你的学习算法。这种做法同样适用于,如果真实函数由 到 映射保持不变,正如此例中,因为真实函数是此图片是否是一只猫,训练你的函数的需要变得更加迫切,如果真实函数也改变,情况就更糟了。
“Covariate shift”的问题怎么应用于神经网络呢?
从第三层隐藏层的角度来看,这些隐藏单元( a 1 [ 2 ] , a 2 [ 2 ] , a 3 [ 2 ] , a 4 [ 2 ] a^{[2]}_{1},a^{[2]}_{2},a_{3}^{[2]},a^{[2]}_{4} a1[2],a2[2],a3[2],a4[2])的值在不断地改变,所以它就有了“Covariate shift”的问题,上张幻灯片中我们讲过的。Batch归一化做的,是它减少了这些隐藏值分布变化的数量。Batch归一化可以确保无论其怎样变化,隐藏单元的均值和方差保持不变,所以即使, z 1 [ 2 ] , . . . z^{[2]}_{1},... z1[2],...值改变,至少他们的均值和方差也会是均值0,方差1,或不一定必须是均值0,方差1,而是由 β \beta β和 γ \gamma γ决定的值。
Batch归一化减少了输入值改变的问题,它的确使这些值变得更稳定,神经网络的之后层就会有更坚实的基础。即使使输入分布改变了一些,它会改变得更少。它做的是当前层保持学习,当改变时,迫使后层适应的程度减小了,你可以这样想,它减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这有助于加速整个网络的学习。
Batch归一化有轻微的正则化效果,因为给隐藏单元添加了噪音,这迫使后部单元不过分依赖任何一个隐藏单元,类似于dropout,它给隐藏层增加了噪音,因此有轻微的正则化效果。因为添加的噪音很微小,所以并不是巨大的正则化效果,你可以将Batch归一化和dropout一起使用,如果你想得到dropout更强大的正则化效果。
也许另一个轻微非直观的效果是,如果你应用了较大的mini-batch,对,比如说,你用了512而不是64,通过应用较大的min-batch,你减少了噪音,因此减少了正则化效果,这是dropout的一个奇怪的性质,就是应用较大的mini-batch可以减少正则化效果。
但是不要把Batch归一化当作正则化,把它当作将你归一化隐藏单元激活值并加速学习的方式,我认为正则化几乎是一个意想不到的副作用。
Batch归一化一次只能处理一个mini-batch数据,它在mini-batch上计算均值和方差。所以测试时,你试图做出预测,试着评估神经网络,你也许没有mini-batch的例子,你也许一次只能进行一个简单的例子,所以测试时,你需要做一些不同的东西以确保你的预测有意义。
测试时的Batch Norm
Batch归一化将你的数据以mini-batch的形式逐一处理,但在测试时,你可能需要对每个样本逐一处理,我们来看一下怎样调整你的网络来做到这一点。
在典型的Batch归一化运用中,你需要用一个指数加权平均来估算,这个平均数涵盖了所有mini-batch;你会这样来追踪你看到的这个均值向量的最新平均值和 σ 2 \sigma^{2} σ2
Softmax回归
到目前为止,我们讲到过的分类的例子都使用了二分分类,这种分类只有两种可能的标记0或1,这是一只猫或者不是一只猫,如果我们有多种可能的类型的话呢?有一种logistic回归的一般形式,叫做Softmax回归,能让你在试图识别某一分类时做出预测,或者说是多种分类中的一个,不只是识别两个分类,我们来一起看一下。
展示一个没有隐藏层的神经网络的softmax分类器的线性决策边界:
训练一个Softmax分类器
损失函数:
L ( y ^ , y ) = − ∑ j = 1 C y i log y ^ j L(\widehat{y},y)=-\sum_{j=1}^{C}y_{i}\log\widehat{y}_{j} L(y ,y)=−∑j=1Cyilogy j
概括来讲,损失函数所做的就是它找到你的训练集中的真实类别,然后试图使该类别相应的概率尽可能地高,如果你熟悉统计学中最大似然估计,这其实就是最大似然估计的一种形式。
代价函数:
J ( w [ 1 ] , b [ 1 ] , . . . ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w^{[1]},b^{[1]},...)=\frac{1}{m}\sum_{i=1}^{m}L(\widehat{y}^{(i)},y^{(i)}) J(w[1],b[1],...)=m1∑i=1mL(y (i),y(i))
这是单个训练样本的损失,整个训练集的损失又如何呢?也就是设定参数的代价之类的,还有各种形式的偏差的代价,它的定义你大致也能猜到,就是整个训练集损失的总和,把你的训练算法对所有训练样本的预测都加起来
因此你要做的就是用梯度下降法,使这里的损失最小化
如果使用矩阵化:
执行梯度下降的反向传播表达式:
d z [ L ] = y ^ − y dz^{[L]}=\widehat{y}-y dz[L]=y −y
(C,1)
深度学习框架
现在有很多好的深度学习软件框架,可以帮助你实现这些模型。类比一下,我猜你知道如何做矩阵乘法,你还应该知道如何编程实现两个矩阵相乘,但是当你在建很大的应用时,你很可能不想用自己的矩阵乘法函数,而是想要访问一个数值线性代数库,它会更高效,但如果你明白两个矩阵相乘是怎么回事还是挺有用的。我认为现在深度学习已经很成熟了,利用一些深度学习框架会更加实用,会使你的工作更加有效,那就让我们来看下有哪些框架。
选择框架的标准:
一个重要的标准就是便于编程,这既包括神经网络的开发和迭代,还包括为产品进行配置,为了成千上百万,甚至上亿用户的实际使用,取决于你想要做什么。
第二个重要的标准是运行速度,特别是训练大数据集时,一些框架能让你更高效地运行和训练神经网络
还有一个标准人们不常提到,但我觉得很重要,那就是这个框架是否真的开放,要是一个框架真的开放,它不仅需要开源,而且需要良好的管理。此我会注意的一件事就是你能否相信这个框架能长时间保持开源,而不是在一家公司的控制之下,它未来有可能出于某种原因选择停止开源,即便现在这个软件是以开源的形式发布的。
TensorFlow
欢迎来到这周的最后一个视频,有很多很棒的深度学习编程框架,其中一个是TensorFlow,我很期待帮助你开始学习使用TensorFlow,我想在这个视频中向你展示TensorFlow程序的基本结构
例题
-
每个超参数如果设置得不好,都会对训练产生巨大的负面影响,因此所有的超参数都要调整好,请问这是正确的吗?
错误(我们在视频中讲到的比如学习率这个超参数比其他的超参数更加重要。)
-
在训练了具有批标准化的神经网络之后,在用新样本评估神经网络的时候,您应该:
- 执行所需的标准化,使用在训练期间,通过指数加权平均值得出的μ和 σ 2 \sigma^{2} σ2
-
在标准化公式 z n o r m ( i ) = z [ i ] − μ σ 2 + ϵ z_{norm}^{(i)}=\frac{z^{[i]-\mu}}{\sqrt{\sigma^{2}+\epsilon}} znorm(i)=σ2+ϵz[i]−μ,为什么要使用epsilon(ϵ)?
- 为了避免除零操作
机器学习(ML)策略(1)
为什么是ML策略
当你尝试优化一个深度学习系统时,你通常可以有很多想法可以去试,问题在于,如果你做出了错误的选择,你完全有可能白费6个月的时间,往错误的方向前进,在6个月之后才意识到这方法根本不管用。比如,我见过一些团队花了6个月时间收集更多数据,却在6个月之后发现,这些数据几乎没有改善他们系统的性能。所以,假设你的项目没有6个月的时间可以浪费,如果有快速有效的方法能够判断哪些想法是靠谱的,或者甚至提出新的想法,判断哪些是值得一试的想法,哪些是可以放心舍弃的。
我希望在这门课程中,可以教给你们一些策略,一些分析机器学习问题的方法,可以指引你们朝着最有希望的方向前进。这门课中,我会和你们分享我在搭建和部署大量深度学习产品时学到的经验和教训,我想这些内容是这门课程独有的。比如说,很多大学深度学习课程很少提到这些策略。事实上,机器学习策略在深度学习的时代也在变化,因为现在对于深度学习算法来说能够做到的事情,比上一代机器学习算法大不一样。我希望这些策略能帮助你们提高效率,让你们的深度学习系统更快投入实用。
正交化
搭建建立机器学习系统的挑战之一是,你可以尝试和改变的东西太多太多了。包括,比如说,有那么多的超参数可以调。我留意到,那些效率很高的机器学习专家有个特点,他们思维清晰,对于要调整什么来达到某个效果,非常清楚,这个步骤我们称之为正交化,让我告诉你是什么意思吧。
如果你的算法在成本函数上不能很好地拟合训练集,你想要一个旋钮,这样你可以用来确保你的可以调整你的算法,让它很好地拟合训练集,所以你用来调试的旋钮是你可能可以训练更大的网络,或者可以切换到更好的优化算法,比如Adam优化算法,等等。我们将在本周和下周讨论一些其他选项。
相比之下,如果发现你的算法在开发/验证集上做的不好,它在训练集上做得很好,但开发集不行,然后你有一组正则化的旋钮可以调节,尝试让系统满足第二个条件。增大训练集可以是另一个可用的旋钮,它可以帮助你的学习算法更好地归纳开发集的规律。
如果系统在开发集上做的很好,但测试集上做得不好呢?如果是这样,那么你需要调的旋钮,可能是更大的开发集。因为如果它在开发集上做的不错,但测试集不行这可能意味着你对开发集过拟合了,你需要往回退一步,使用更大的开发集。
最后,如果它在测试集上做得很好,但无法给你的猫图片应用用户提供良好的体验,这意味着你需要回去,改变开发集或成本函数。因为如果根据某个成本函数,系统在测试集上做的很好,但它无法反映你的算法在现实世界中的表现,这意味着要么你的开发集分布设置不正确,要么你的成本函数测量的指标不对。
当我训练神经网络时,我一般不用early stopping,这个技巧也还不错,很多人都这么干。但个人而言,我觉得用early stopping有点难以分析,因为这个旋钮会同时影响你对训练集的拟合,因为如果你早期停止,那么对训练集的拟合就不太好,但它同时也用来改善开发集的表现,所以这个旋钮没那么正交化。因为它同时影响两件事情,就像一个旋钮同时影响电视图像的宽度和高度。不是说这样就不要用,如果你想用也是可以的。但如果你有更多的正交化控制,比如我这里写出的其他手段,用这些手段调网络会简单不少。
在机器学习中,如果你可以观察你的系统,然后说这一部分是错的,它在训练集上做的不好、在开发集上做的不好、它在测试集上做的不好,或者它在测试集上做的不错,但在现实世界中不好,这就很好。必须弄清楚到底是什么地方出问题了,然后我们刚好有对应的旋钮,或者一组对应的旋钮,刚好可以解决那个问题,那个限制了机器学习系统性能的问题。
单一数字评估指标
无论你是调整超参数,或者是尝试不同的学习算法,或者在搭建机器学习系统时尝试不同手段,你会发现,如果你有一个单实数评估指标,你的进展会快得多,它可以快速告诉你,新尝试的手段比之前的手段好还是差。所以当团队开始进行机器学习项目时,我经常推荐他们为问题设置一个单实数评估指标。
我们来看一个例子,你之前听过我说过,应用机器学习是一个非常经验性的过程,我们通常有一个想法,编程序,跑实验,看看效果如何,然后使用这些实验结果来改善你的想法,然后继续走这个循环,不断改进你的算法。
比如说对于你的猫分类器,之前你搭建了某个分类器A,通过改变超参数,还有改变训练集等手段,你现在训练出来了一个新的分类器B,所以评估你的分类器的一个合理方式是观察它的查准率(precision)和查全率(recall)。
简而言之,查准率的定义是在你的分类器标记为猫的例子中,有多少真的是猫。所以如果分类器A有95%的查准率,这意味着你的分类器说这图有猫的时候,有95%的机会真的是猫。
查全率就是,对于所有真猫的图片,你的分类器正确识别出了多少百分比。实际为猫的图片中,有多少被系统识别出来?如果分类器查A全率是90%,这意味着对于所有的图像,比如说你的开发集都是真的猫图,分类器准确地分辨出了其中的90%。
事实证明,查准率和查全率之间往往需要折衷,两个指标都要顾及到。如果你尝试了很多不同想法,很多不同的超参数,你希望能够快速试验不仅仅是两个分类器,也许是十几个分类器,快速选出“最好的”那个,这样你可以从那里出发再迭代。如果有两个评估指标,就很难去快速地二中选一或者十中选一,所以我并不推荐使用两个评估指标,查准率和查全率来选择一个分类器。你只需要找到一个新的评估指标,能够结合查准率和查全率。
在机器学习文献中,结合查准率和查全率的标准方法是所谓的 F 1 F_{1} F1分数, F 1 F_{1} F1分数的细节并不重要。但非正式的,你可以认为这是查准率 P P P和查全率 R R R的平均值。正式来看, F 1 F_{1} F1分数的定义是这个公式: 2 1 P + 1 R \frac{2}{\frac{1}{P}+\frac{1}{R}} P1+R12
在数学中,这个函数叫做查准率 P P P和查全率 R R R的调和平均数。但非正式来说,你可以将它看成是某种查准率和查全率的平均值,只不过你算的不是直接的算术平均,而是用这个公式定义的调和平均。这个指标在权衡查准率和查全率时有一些优势。
对于这个例子,我建议,除了跟踪分类器在四个不同的地理大区的表现,也要算算平均值。假设平均表现是一个合理的单实数评估指标,通过计算平均值,你就可以快速判断
满足和优化指标
要把你顾及到的所有事情组合成单实数评估指标有时并不容易,在那些情况里,我发现有时候设立满足和优化指标是很重要的,让我告诉你是什么意思吧。
假设你已经决定你很看重猫分类器的分类准确度,这可以是 F 1 F_{1} F1分数或者用其他衡量准确度的指标。但除了准确度之外,我们还需要考虑运行时间,就是需要多长时间来分类一张图。分类器需要80毫秒,需要95毫秒,需要1500毫秒,就是说需要1.5秒来分类图像。
你可以这么做,将准确度和运行时间组合成一个整体评估指标。所以成本 c o s t = a c c u r a c y − 0.5 × r u n n i n g T i m e cost=accuracy-0.5{\times}runningTime cost=accuracy−0.5×runningTime,比如说,总体成本是,这种组合方式可能太刻意,只用这样的公式来组合准确度和运行时间,两个数值的线性加权求和。
你还可以做其他事情,就是你可能选择一个分类器,能够最大限度提高准确度,但必须满足运行时间要求,就是对图像进行分类所需的时间必须小于等于100毫秒。所以在这种情况下,我们就说准确度是一个优化指标,因为你想要准确度最大化,你想做的尽可能准确,但是运行时间就是我们所说的满足指标,意思是它必须足够好,它只需要小于100毫秒,达到之后,你不在乎这指标有多好,或者至少你不会那么在乎。所以这是一个相当合理的权衡方式,或者说将准确度和运行时间结合起来的方式。实际情况可能是,只要运行时间少于100毫秒,你的用户就不会在乎运行时间是100毫秒还是50毫秒,甚至更快。
通过定义优化和满足指标,就可以给你提供一个明确的方式,去选择“最好的”分类器。在这种情况下分类器B最好,因为在所有的运行时间都小于100毫秒的分类器中,它的准确度最好。
所以更一般地说,如果你要考虑 N N N个指标,有时候选择其中一个指标做为优化指标是合理的。所以你想尽量优化那个指标,然后剩下个 N − 1 N-1 N−1指标都是满足指标,意味着只要它们达到一定阈值,例如运行时间快于100毫秒,但只要达到一定的阈值,你不在乎它超过那个门槛之后的表现,但它们必须达到这个门槛。
总结一下,如果你需要顾及多个指标,比如说,有一个优化指标,你想尽可能优化的,然后还有一个或多个满足指标,需要满足的,需要达到一定的门槛。现在你就有一个全自动的方法,在观察多个成本大小时,选出"最好的"那个。现在这些评估指标必须是在训练集或开发集或测试集上计算或求出来的。所以你还需要做一件事,就是设立训练集、开发集,还有测试集。
训练/开发/测试集划分
设立训练集,开发集和测试集的方式大大影响了你或者你的团队在建立机器学习应用方面取得进展的速度。同样的团队,即使是大公司里的团队,在设立这些数据集的方式,真的会让团队的进展变慢而不是加快,我们看看应该如何设立这些数据集,让你的团队效率最大化。
在这个视频中,我想集中讨论如何设立开发集和测试集,开发(dev)集也叫做开发集(development set),有时称为保留交叉验证集(hold out cross validation set)。
然后,机器学习中的工作流程是,你尝试很多思路,用训练集训练不同的模型,然后使用开发集来评估不同的思路,然后选择一个,然后不断迭代去改善开发集的性能,直到最后你可以得到一个令你满意的成本,然后你再用测试集去评估。
现在,举个例子,你要开发一个猫分类器,然后你在这些区域里运营,美国、英国、其他欧洲国家,南美洲、印度、中国,其他亚洲国家和澳大利亚,那么你应该如何设立开发集和测试集呢?
事实证明,这个想法非常糟糕,因为这个例子中,你的开发集和测试集来自不同的分布。我建议你们不要这样,而是让你的开发集和测试集来自同一分布。所以,为了避免这种情况,我建议的是你将所有数据随机洗牌,放入开发集和测试集,所以开发集和测试集都有来自八个地区的数据,并且开发集和测试集都来自同一分布,这分布就是你的所有数据混在一起。
所以我建议你们在设立开发集和测试集时,要选择这样的开发集和测试集,能够反映你未来会得到的数据,认为很重要的数据,必须得到好结果的数据,特别是,这里的开发集和测试集可能来自同一个分布。所以不管你未来会得到什么样的数据,一旦你的算法效果不错,要尝试收集类似的数据,而且,不管那些数据是什么,都要随机分配到开发集和测试集上。因为这样,你才能将瞄准想要的目标,让你的团队高效迭代来逼近同一个目标,希望最好是同一个目标。
我们还没提到如何设立训练集,我们会在之后的视频里谈谈如何设立训练集,但这个视频的重点在于,设立开发集以及评估指标,真的就定义了你要瞄准的目标。我们希望通过在同一分布中设立开发集和测试集,你就可以瞄准你所希望的机器学习团队瞄准的目标。而设立训练集的方式则会影响你逼近那个目标有多快,但我们可以在另一个讲座里提到。我知道有一些机器学习团队,他们如果能遵循这个方针,就可以省下几个月的工作,所以我希望这些方针也能帮到你们。
开发集和测试集的大小
在上一个视频中你们知道了你的开发集和测试集为什么必须来自同一分布,但它们规模应该多大?在深度学习时代,设立开发集和测试集的方针也在变化,我们来看看一些最佳做法。
所以在现代深度学习时代,有时我们拥有大得多的数据集,所以使用小于20%的比例或者小于30%比例的数据作为开发集和测试集也是合理的。而且因为深度学习算法对数据的胃口很大,我们可以看到那些有海量数据集的问题,有更高比例的数据划分到训练集里,那么测试集呢?
要记住,测试集的目的是完成系统开发之后,测试集可以帮你评估投产系统的性能。方针就是,令你的测试集足够大,能够以高置信度评估系统整体性能。所以除非你需要对最终投产系统有一个很精确的指标,一般来说测试集不需要上百万个例子。对于你的应用程序,也许你想,有10,000个例子就能给你足够的置信度来给出性能指标了,也许100,000个之类的可能就够了,这数目可能远远小于比如说整体数据集的30%,取决于你有多少数据。
总结一下,在大数据时代旧的经验规则,这个70/30不再适用了。现在流行的是把大量数据分到训练集,然后少量数据分到开发集和测试集,特别是当你有一个非常大的数据集时。以前的经验法则其实是为了确保开发集足够大,能够达到它的目的,就是帮你评估不同的想法,然后选出还是更好。测试集的目的是评估你最终的成本偏差,你只需要设立足够大的测试集,可以用来这么评估就行了,可能只需要远远小于总体数据量的30%。
所以我希望本视频能给你们一点指导和建议,让你们知道如何在深度学习时代设立开发和测试集。接下来,有时候在研究机器学习的问题途中,你可能需要更改评估指标,或者改动你的开发集和测试集,我们会讲什么时候需要这样做。
什么时候该改变开发/测试集和指标
你已经学过如何设置开发集和评估指标,就像是把目标定在某个位置,让你的团队瞄准。但有时候在项目进行途中,你可能意识到,目标的位置放错了。这种情况下,你应该移动你的目标。
但粗略的结论是,如果你的评估指标无法正确评估好算法的排名,那么就需要花时间定义一个新的评估指标。这是定义评估指标的其中一种可能方式(上述加权法)。评估指标的意义在于,准确告诉你已知两个分类器,哪一个更适合你的应用。就这个视频的内容而言,我们不需要太注重新错误率指标是怎么定义的,关键在于,如果你对旧的错误率指标不满意,那就不要一直沿用你不满意的错误率指标,而应该尝试定义一个新的指标,能够更加符合你的偏好,定义出实际更适合的算法。
总体方针就是,如果你当前的指标和当前用来评估的数据和你真正关心必须做好的事情关系不大,那就应该更改你的指标或者你的开发测试集,让它们能更够好地反映你的算法需要处理好的数据。
有一个评估指标和开发集让你可以更快做出决策,判断算法还是算法更优,这真的可以加速你和你的团队迭代的速度。所以我的建议是,即使你无法定义出一个很完美的评估指标和开发集,你直接快速设立出来,然后使用它们来驱动你们团队的迭代速度。如果在这之后,你发现选的不好,你有更好的想法,那么完全可以马上改。对于大多数团队,我建议最好不要在没有评估指标和开发集时跑太久,因为那样可能会减慢你的团队迭代和改善算法的速度。本视频讲的是什么时候需要改变你的评估指标和开发测试集,我希望这些方针能让你的整个团队设立一个明确的目标,一个你们可以高效迭代,改善性能的目标。
为什么是人的表现?
在过去的几年里,更多的机器学习团队一直在讨论如何比较机器学习系统和人类的表现,为什么呢?
我认为有两个主要原因,首先是因为深度学习系统的进步,机器学习算法突然变得更好了。在许多机器学习的应用领域已经开始见到算法已经可以威胁到人类的表现了。其次,事实证明,当你试图让机器做人类能做的事情时,可以精心设计机器学习系统的工作流程,让工作流程效率更高,所以在这些场合,比较人类和机器是很自然的,或者你要让机器模仿人类的行为。
事实证明,机器学习的进展往往相当快,直到你超越人类的表现之前一直很快,当你超越人类的表现时,有时进展会变慢。我认为有两个原因,为什么当你超越人类的表现时,进展会慢下来。一个原因是人类水平在很多任务中离贝叶斯最优错误率(贝叶斯最优错误率有时写作Bayesian,即省略optimal,就是从 x x x到 y y y映射的理论最优函数,永远不会被超越)已经不远了,人们非常擅长看图像,分辨里面有没有猫或者听写音频。所以,当你超越人类的表现之后也许没有太多的空间继续改善了。但第二个原因是,只要你的表现比人类的表现更差,那么实际上可以使用某些工具来提高性能。一旦你超越了人类的表现,这些工具就没那么好用了。
可避免偏差
我们讨论过,你希望你的学习算法能在训练集上表现良好,但有时你实际上并不想做得太好。你得知道人类水平的表现是怎样的,可以确切告诉你算法在训练集上的表现到底应该有多好,或者有多不好,让我告诉你是什么意思吧。
所以要解释这里发生的事情,用人类水平的错误率估计或代替贝叶斯错误率或贝叶斯最优错误率,对于计算机视觉任务而言,这样替代相当合理,因为人类实际上是非常擅长计算机视觉任务的,所以人类能做到的水平和贝叶斯错误率相差不远。根据定义,人类水平错误率比贝叶斯错误率高一点,因为贝叶斯错误率是理论上限,但人类水平错误率离贝叶斯错误率不会太远。所以这里比较意外的是取决于人类水平错误率有多少,或者这真的就很接近贝叶斯错误率,所以我们假设它就是,但取决于我们认为什么样的水平是可以实现的。
所以要给这些概念命名一下,这不是广泛使用的术语,但我觉得这么说思考起来比较流畅。就是把这个差值,贝叶斯错误率或者对贝叶斯错误率的估计和训练错误率之间的差值称为可避免偏差,你可能希望一直提高训练集表现,直到你接近贝叶斯错误率,但实际上你也不希望做到比贝叶斯错误率更好,这理论上是不可能超过贝叶斯错误率的,除非过拟合。而这个训练错误率和开发错误率之前的差值,就大概说明你的算法在方差问题上还有多少改善空间。
所以在这个例子中,当你理解人类水平错误率,理解你对贝叶斯错误率的估计,你就可以在不同的场景中专注于不同的策略,使用避免偏差策略还是避免方差策略。在训练时如何考虑人类水平表现来决定工作着力点,具体怎么做还有更多微妙的细节,所以在下一个视频中,我们会深入了解人类水平表现的真正意义。
理解人的表现
人类水平表现这个词在论文里经常随意使用,但我现在告诉你这个词更准确的定义,特别是使用人类水平表现这个词的定义,可以帮助你们推动机器学习项目的进展。还记得上个视频中,我们用过这个词“人类水平错误率”用来估计贝叶斯误差,那就是理论最低的错误率,任何函数不管是现在还是将来,能够到达的最低值。
本视频的要点是,在定义人类水平错误率时,要弄清楚你的目标所在,如果要表明你可以超越单个人类,那么就有理由在某些场合部署你的系统,也许这个定义是合适的。但是如果您的目标是替代贝叶斯错误率,那么这个定义(经验丰富的医生团队——0.5%)才合适。
什么时候真正有效呢?
就是比如你的训练错误率是0.7%,所以你现在已经做得很好了,你的开发错误率是0.8%。在这种情况下,你用0.5%来估计贝叶斯错误率关系就很大。因为在这种情况下,你测量到的可避免偏差是0.2%,这是你测量到的方差问题0.1%的两倍,这表明也许偏差和方差都存在问题。但是,可避免偏差问题更严重。在这个例子中,我们在上一张幻灯片中讨论的是0.5%,就是对贝叶斯错误率的最佳估计,因为一群人类医生可以实现这一目标。如果你用0.7代替贝叶斯错误率,你测得的可避免偏差基本上是0%,那你就可能忽略可避免偏差了。实际上你应该试试能不能在训练集上做得更好。
总结一下我们讲到的,如果你想理解偏差和方差,那么在人类可以做得很好的任务中,你可以估计人类水平的错误率,你可以使用人类水平错误率来估计贝叶斯错误率。所以你到贝叶斯错误率估计值的差距,告诉你可避免偏差问题有多大,可避免偏差问题有多严重,而训练错误率和开发错误率之间的差值告诉你方差上的问题有多大,你的算法是否能够从训练集泛化推广到开发集。
今天讲的和之前课程中见到的重大区别是,以前你们比较的是训练错误率和0%,直接用这个值估计偏差。相比之下,在这个视频中,我们有一个更微妙的分析,其中并没有假设你应该得到0%错误率,因为有时贝叶斯错误率是非零的,有时基本不可能做到比某个错误率阈值更低。当数据噪点很多时,比如背景声音很嘈杂的语言识别,有时几乎不可能听清楚说的是什么,并正确记录下来。对于这样的问题,更好的估计贝叶斯错误率很有必要,可以帮助你更好地估计可避免偏差和方差,这样你就能更好的做出决策,选择减少偏差的策略,还是减少方差的策略。
回顾一下,对人类水平有大概的估计可以让你做出对贝叶斯错误率的估计,这样可以让你更快地作出决定是否应该专注于减少算法的偏差,或者减少算法的方差。这个决策技巧通常很有效,直到你的系统性能开始超越人类,那么你对贝叶斯错误率的估计就不再准确了,但这些技巧还是可以帮你做出明确的决定。
超过人的表现
很多团队会因为机器在特定的识别分类任务中超越了人类水平而激动不已,我们谈谈这些情况,看看你们自己能不能达到。
我们讨论过机器学习进展,会在接近或者超越人类水平的时候变得越来越慢。
现在,机器学习有很多问题已经可以大大超越人类水平了。例如,我想网络广告,估计某个用户点击广告的可能性,可能学习算法做到的水平已经超越任何人类了。还有提出产品建议,向你推荐电影或书籍之类的任务。我想今天的网站做到的水平已经超越你最亲近的朋友了。还有物流预测,从A到B开车需要多久,或者预测快递车从A开B到需要多少时间。或者预测某人会不会偿还贷款,这样你就能判断是否批准这人的贷款。我想这些问题都是今天的机器学习远远超过了单个人类的表现。
请注意这四个例子,所有这四个例子都是从结构化数据中学习得来的,这里你可能有个数据库记录用户点击的历史,你的购物历史数据库,或者从A到B需要多长时间的数据库,以前的贷款申请及结果的数据库,这些并不是自然感知问题,这些不是计算机视觉问题,或语音识别,或自然语言处理任务。人类在自然感知任务中往往表现非常好,所以有可能对计算机来说在自然感知任务的表现要超越人类要更难一些。
除了这些问题,今天已经有语音识别系统超越人类水平了,还有一些计算机视觉任务,一些图像识别任务,计算机已经超越了人类水平。但是由于人类对这种自然感知任务非常擅长,我想计算机达到那种水平要难得多。还有一些医疗方面的任务,比如阅读ECG或诊断皮肤癌,或者某些特定领域的放射科读图任务,这些任务计算机做得非常好了,也许超越了单个人类的水平。
在深度学习的最新进展中,其中一个振奋人心的方面是,即使在自然感知任务中,在某些情况下,计算机已经可以超越人类的水平了。不过现在肯定更加困难,因为人类一般很擅长这种自然感知任务。
所以要达到超越人类的表现往往不容易,但如果有足够多的数据,已经有很多深度学习系统,在单一监督学习问题上已经超越了人类的水平,所以这对你在开发的应用是有意义的。我希望有一天你也能够搭建出超越人类水平的深度学习系统。
改善你的模型的表现
你们学过正交化,如何设立开发集和测试集,用人类水平错误率来估计贝叶斯错误率以及如何估计可避免偏差和方差。我们现在把它们全部组合起来写成一套指导方针,如何提高学习算法性能的指导方针。
总结一下前几段视频我们见到的步骤,如果你想提升机器学习系统的性能,我建议你们看看训练错误率和贝叶斯错误率估计值之间的距离,让你知道可避免偏差有多大。换句话说,就是你觉得还能做多好,你对训练集的优化还有多少空间。然后看看你的开发错误率和训练错误率之间的距离,就知道你的方差问题有多大。换句话说,你应该做多少努力让你的算法表现能够从训练集推广到开发集,算法是没有在开发集上训练的。
如果你想用尽一切办法减少可避免偏差,我建议试试这样的策略:比如使用规模更大的模型,这样算法在训练集上的表现会更好,或者训练更久。使用更好的优化算法,比如说加入momentum或者RMSprop,或者使用更好的算法,比如Adam。你还可以试试寻找更好的新神经网络架构,或者说更好的超参数。这些手段包罗万有,你可以改变激活函数,改变层数或者隐藏单位数,虽然你这么做可能会让模型规模变大。或者试用其他模型,其他架构,如循环神经网络和卷积神经网络。在之后的课程里我们会详细介绍的,新的神经网络架构能否更好地拟合你的训练集,有时也很难预先判断,但有时换架构可能会得到好得多的结果。
另外当你发现方差是个问题时,你可以试用很多技巧,包括以下这些:你可以收集更多数据,因为收集更多数据去训练可以帮你更好地推广到系统看不到的开发集数据。你可以尝试正则化,包括 L 2 L2 L2正则化,dropout正则化或者我们在之前课程中提到的数据增强。同时你也可以试用不同的神经网络架构,超参数搜索,看看能不能帮助你,找到一个更适合你的问题的神经网络架构。
我想这些偏差、可避免偏差和方差的概念是容易上手,难以精通的。如果你能系统全面地应用本周课程里的概念,你实际上会比很多现有的机器学习团队更有效率、更系统、更有策略地系统提高机器学习系统的性能。
例题
-
现在你是和平之城的著名研究员,和平之城的人有一个共同的特点:他们害怕鸟类。为了保护他们,你必须设计一个算法,以检测飞越和平之城的任何鸟类,同时警告人们有鸟类飞过。市议会为你提供了10,000,000张图片的数据集,这些都是从城市的安全摄像头拍摄到的。在设置了训练/开发/测试集之后,市议会再次给你了1,000,000张图片,称为“公民数据”。 显然,和平之城的公民非常害怕鸟类,他们自愿为天空拍照并贴上标签,从而为这些额外的1,000,000张图像贡献力量。 这些图像与市议会最初给您的图像分布不同,但您认为它可以帮助您的算法。市议会的一名成员对机器学习知之甚少,他认为应该将1,000,000个公民的数据图像添加到测试集中,你反对的原因是:
- 这会导致开发集和测试集分布变得不同。这是一个很糟糕的主意,因为这会达不到你想要的效果
- 测试集不再反映您最关心的数据(安全摄像头)的分布
-
你发现一组鸟类学家辩论和讨论图像,可以得到一个更好的0.1%的性能,所以你将其定义为“人类表现”。在对算法进行深入研究之后,最终得出以下结论:
人类表现 0.1%
训练集误差 2.0%
开发集误差 2.1%根据你的资料,以下四个选项中哪两个尝试起来是最有希望的?(两个选项)
- 尝试减少正则化
- 训练一个更大的模型,试图在训练集上做得更好。
-
你在测试集上评估你的模型,并找到以下内容:
人类表现 0.1%
训练集误差 2.0%
开发集误差 2.1%
测试集误差 7.0%这意味着什么?(两个最佳选项)
- 你应该尝试获得更大的开发集
- 你对开发集过拟合了
-
市议会认为在城市里养更多的猫会有助于吓跑鸟类,他们对你在鸟类探测器上的工作感到非常满意,他们也雇佣你来设计一个猫探测器。由于有多年的猫探测器的工作经验,你有一个巨大的数据集,你有100,000,000猫的图像,训练这个数据需要大约两个星期。你同意哪些说法?(选出所有正确项)
- 需要两周的时间来训练将会限制你迭代的速度。
- 购买速度更快的计算机可以加速团队的迭代速度,从而提高团队的生产力。
- 如果10,000,000个样本就足以建立一个足够好的猫探测器,你最好用10,000,00个样本训练,从而使您可以快速运行实验的速度提高约10倍,即使每个模型表现差一点因为它的训练数据较少。
机器学习(ML)策略(2)
进行误差分析
如果你希望让学习算法能够胜任人类能做的任务,但你的学习算法还没有达到人类的表现,那么人工检查一下你的算法犯的错误也许可以让你了解接下来应该做什么。这个过程称为错误分析
假设你正在调试猫分类器,然后你取得了90%准确率,相当于10%错误,在你的开发集上做到这样,这离你希望的目标还有很远。也许你的队员看了一下算法分类出错的例子,注意到算法将一些狗分类为猫
首先,收集一下,比如说100个错误标记的开发集样本,然后手动检查,一次只看一个,看看你的开发集里有多少错误标记的样本是狗。
现在,假设事实上,你的100个错误标记样本中只有5%是狗,就是说在100个错误标记的开发集样本中,有5个是狗。这意味着100个样本,在典型的100个出错样本中,即使你完全解决了狗的问题,你也只能修正这100个错误中的5个。或者换句话说,如果只有5%的错误是狗图片,那么如果你在狗的问题上花了很多时间,那么你最多只能希望你的错误率从10%下降到9.5%。你就可以确定这样花时间不好,或者也许应该花时间,但至少这个分析给出了一个上限。如果你继续处理狗的问题,能够改善算法性能的上限,对吧?在机器学习中,有时我们称之为性能上限,就意味着,最好能到哪里,完全解决狗的问题可以对你有多少帮助。
但现在,假设发生了另一件事,假设我们观察一下这100个错误标记的开发集样本,你发现实际有50张图都是狗,所以有50%都是狗的照片,现在花时间去解决狗的问题可能效果就很好。这种情况下,如果你真的解决了狗的问题,那么你的错误率可能就从10%下降到5%了。
我知道在机器学习中,有时候我们很鄙视手工操作,或者使用了太多人为数值。但如果你要搭建应用系统,那这个简单的人工统计步骤,错误分析,可以节省大量时间,可以迅速决定什么是最重要的,或者最有希望的方向。实际上,如果你观察100个错误标记的开发集样本,也许只需要5到10分钟的时间,亲自看看这100个样本,并亲自统计一下有多少是狗。根据结果,看看有没有占到5%、50%或者其他东西。这个在5到10分钟之内就能给你估计这个方向有多少价值,并且可以帮助你做出更好的决定,是不是把未来几个月的时间投入到解决错误标记的狗图这个问题。
有时你在做错误分析时,也可以同时并行评估几个想法。如下图。也许你有些想法,知道大概怎么处理这些问题,要进行错误分析来评估这三个想法。
我会做的是建立这样一个表格,在最左边,人工过一遍你想分析的图像集,所以图像可能是从1到100,如果你观察100张图的话。电子表格的一列就对应你要评估的想法,所以狗的问题,猫科动物的问题,模糊图像的问题,我通常也在电子表格中留下空位来写评论。所以记住,在错误分析过程中,你就看看算法识别错误的开发集样本,如果你发现第一张识别错误的图片是狗图,那么我就在那里打个勾,为了帮我自己记住这些图片,有时我会在评论里注释,也许这是一张比特犬的图。如果第二张照片很模糊,也记一下。如果第三张是在下雨天动物园里的狮子,被识别成猫了,这是大型猫科动物,还有图片模糊,在评论部分写动物园下雨天,是雨天让图像模糊的之类的。最后,这组图像过了一遍之后,我可以统计这些算法(错误)的百分比,或者这里每个错误类型的百分比,有多少是狗,大猫或模糊这些错误类型。所以也许你检查的图像中8%是狗,可能43%属于大猫,61%属于模糊。这意味着扫过每一列,并统计那一列有多少百分比图像打了勾。
在这个步骤做到一半时,有时你可能会发现其他错误类型,比如说你可能发现有Instagram滤镜,那些花哨的图像滤镜,干扰了你的分类器。在这种情况下,实际上可以在错误分析途中,增加这样一列,比如多色滤镜 Instagram滤镜和Snapchat滤镜,然后再过一遍,也统计一下那些问题,并确定这个新的错误类型占了多少百分比,这个分析步骤的结果可以给出一个估计,是否值得去处理每个不同的错误类型。
例如,在这个样本中,有很多错误来自模糊图片,也有很多错误类型是大猫图片。所以这个分析的结果不是说你一定要处理模糊图片,这个分析没有给你一个严格的数学公式,告诉你应该做什么,但它能让你对应该选择那些手段有个概念。它也告诉你,比如说不管你对狗图片或者Instagram图片处理得有多好,在这些例子中,你最多只能取得8%或者12%的性能提升。而在大猫图片这一类型,你可以做得更好。或者模糊图像,这些类型有改进的潜力。这些类型里,性能提高的上限空间要大得多。
所以总结一下,进行错误分析,你应该找一组错误样本,可能在你的开发集里或者测试集里,观察错误标记的样本,看看假阳性(false positives)和假阴性(false negatives),统计属于不同错误类型的错误数量。在这个过程中,你可能会得到启发,归纳出新的错误类型,就像我们看到的那样。如果你过了一遍错误样本,然后说,天,有这么多Instagram滤镜或Snapchat滤镜,这些滤镜干扰了我的分类器,你就可以在途中新建一个错误类型。总之,通过统计不同错误标记类型占总数的百分比,可以帮你发现哪些问题需要优先解决,或者给你构思新优化方向的灵感。在做错误分析的时候,有时你会注意到开发集里有些样本被错误标记了,这时应该怎么做呢?我们下一个视频来讨论。
清楚标注错误的数据
你的监督学习问题的数据由输入 x x x和输出标签 y y y构成,如果你观察一下你的数据,并发现有些输出标签 y y y是错的。你的数据有些标签是错的,是否值得花时间去修正这些标签呢?
首先,我们来考虑训练集,事实证明,深度学习算法对于训练集中的随机错误是相当健壮的(robust)。只要你的标记出错的样本,只要这些错误样本离随机错误不太远,有时可能做标记的人没有注意或者不小心,按错键了,如果错误足够随机,那么放着这些错误不管可能也没问题,而不要花太多时间修复它们。
当然你浏览一下训练集,检查一下这些标签,并修正它们也没什么害处。有时候修正这些错误是有价值的,有时候放着不管也可以,只要总数据集总足够大,实际错误率可能不会太高。我见过一大批机器学习算法训练的时候,明知训练集里有 x x x个错误标签,但最后训练出来也没问题。
我这里先警告一下,深度学习算法对随机误差很健壮,但对系统性的错误就没那么健壮了。所以比如说,如果做标记的人一直把白色的狗标记成猫,那就成问题了。因为你的分类器学习之后,会把所有白色的狗都分类为猫。但随机错误或近似随机错误,对于大多数深度学习算法来说不成问题。
现在,之前的讨论集中在训练集中的标记出错的样本,那么如果是开发集和测试集中有这些标记出错的样本呢?如果你担心开发集或测试集上标记出错的样本带来的影响,他们一般建议你在错误分析时,添加一个额外的列,这样你也可以统计标签 y = 1 y=1 y=1错误的样本数。
所以现在问题是,是否值得修正这6%标记出错的样本,我的建议是,如果这些标记错误严重影响了你在开发集上评估算法的能力,那么就应该去花时间修正错误的标签。但是,如果它们没有严重影响到你用开发集评估成本偏差的能力,那么可能就不应该花宝贵的时间去处理。
建议你看3个数字来确定是否值得去人工修正标记出错的数据,我建议你看看整体的开发集错误率,在我们以前的视频中的样本,我们说也许我们的系统达到了90%整体准确度,所以有10%错误率,那么你应该看看错误标记引起的错误的数量或者百分比。所以在这种情况下,6%的错误来自标记出错,所以10%的6%就是0.6%。也许你应该看看其他原因导致的错误,如果你的开发集上有10%错误,其中0.6%是因为标记出错,剩下的占9.4%,是其他原因导致的,比如把狗误认为猫,大猫图片。所以在这种情况下,我说有9.4%错误率需要集中精力修正,而标记出错导致的错误是总体错误的一小部分而已,所以如果你一定要这么做,你也可以手工修正各种错误标签,但也许这不是当下最重要的任务。
我们再看另一个样本,假设你在学习问题上取得了很大进展,所以现在错误率不再是10%了,假设你把错误率降到了2%,但总体错误中的0.6%还是标记出错导致的。所以现在,如果你想检查一组标记出错的开发集图片,开发集数据有2%标记错误了,那么其中很大一部分,0.6%除以2%,实际上变成30%标签而不是6%标签了。有那么多错误样本其实是因为标记出错导致的,所以现在其他原因导致的错误是1.4%。当测得的那么大一部分的错误都是开发集标记出错导致的,那似乎修正开发集里的错误标签似乎更有价值。
如果你还记得设立开发集的目标的话,开发集的主要目的是,你希望用它来从两个分类器 A A A和 B B B中选择一个。所以当你测试两个分类器A和B时,在开发集上一个有2.1%错误率,另一个有1.9%错误率,但是你不能再信任开发集了,因为它无法告诉你这个分类器是否比这个好,因为0.6%的错误率是标记出错导致的。那么现在你就有很好的理由去修正开发集里的错误标签,因为在右边这个样本中,标记出错对算法错误的整体评估标准有严重的影响。而左边的样本中,标记出错对你算法影响的百分比还是相对较小的。
现在如果你决定要去修正开发集数据,手动重新检查标签,并尝试修正一些标签,这里还有一些额外的方针和原则需要考虑。不管用什么修正手段,都要同时作用到开发集和测试集上。如果你打算修正开发集上的部分数据,那么最好也对测试集做同样的修正以确保它们继续来自相同的分布。所以我们雇佣了一个人来仔细检查这些标签,但必须同时检查开发集和测试集。
其次,我强烈建议你要考虑同时检验算法判断正确和判断错误的样本
最后,如果你进入到一个开发集和测试集去修正这里的部分标签,你可能会,也可能不会去对训练集做同样的事情,还记得我们在其他视频里讲过,修正训练集中的标签其实相对没那么重要,你可能决定只修正开发集和测试集中的标签,因为它们通常比训练集小得多,你可能不想把所有额外的精力投入到修正大得多的训练集中的标签,所以这样其实是可以的。
你的开发集和测试集来自同一分布非常重要。但如果你的训练集来自稍微不同的分布,通常这是一件很合理的事情,我会在本周晚些时候谈谈如何处理这个问题。
快速搭建你的第一个系统,并进行迭代
建议如果你想搭建全新的机器学习程序,就是快速搭好你的第一个系统,然后开始迭代。建议你快速设立开发集和测试集还有指标;然后我建议你马上搭好一个机器学习系统原型,然后找到训练集,训练一下,看看效果,开始理解你的算法表现如何,在开发集测试集,你的评估指标上表现如何。当你建立第一个系统后,你就可以马上用到之前说的偏差方差分析,还有之前最后几个视频讨论的错误分析,来确定下一步优先做什么。
所以我希望这些策略有帮助,如果你将机器学习算法应用到新的应用程序里,你的主要目标是弄出能用的系统,你的主要目标并不是发明全新的机器学习算法,这是完全不同的目标,那时你的目标应该是想出某种效果非常好的算法。所以我鼓励你们搭建快速而粗糙的实现,然后用它做偏差/方差分析,用它做错误分析,然后用分析结果确定下一步优先要做的方向。
使用来自不同分布的数据,进行训练和测试
深度学习算法对训练数据的胃口很大,当你收集到足够多带标签的数据构成训练集时,算法效果最好,这导致很多团队用尽一切办法收集数据,然后把它们堆到训练集里,让训练的数据量更大,即使有些数据,甚至是大部分数据都来自和开发集、测试集不同的分布。在深度学习时代,越来越多的团队都用来自和开发集、测试集分布不同的数据来训练,这里有一些微妙的地方,一些最佳做法来处理训练集和测试集存在差异的情况,我们来看看。
例如:
你有一个相对小的数据集,只有10,000个样本来自那个分布(来自应用上传的数据),而你还有一个大得多的数据集来自另一个分布,图片的外观和你真正想要处理的并不一样。但你又不想直接用这10,000张图片,因为这样你的训练集就太小了,使用这20万张图片似乎有帮助。但是,困境在于,这20万张图片并不完全来自你想要的分布,那么你可以怎么做呢?
这里有一种选择,你可以做的一件事是将两组数据合并在一起,这样你就有21万张照片,你可以把这21万张照片随机分配到训练、开发和测试集中。为了说明观点,我们假设你已经确定开发集和测试集各包含2500个样本,所以你的训练集有205000个样本。现在这么设立你的数据集有一些好处,也有坏处。好处在于,你的训练集、开发集和测试集都来自同一分布,这样更好管理。但坏处在于,这坏处还不小,就是如果你观察开发集,看看这2500个样本其中很多图片都来自网页下载的图片,那并不是你真正关心的数据分布,你真正要处理的是来自手机的图片。
你的大部分精力都用在优化来自网页下载的图片,这其实不是你想要的。所以我真的不建议使用第一个选项,因为这样设立开发集就是告诉你的团队,针对不同于你实际关心的数据分布去优化,所以不要这么做。
我建议你走另外一条路,就是这样,训练集,比如说还是205,000张图片,我们的训练集是来自网页下载的200,000张图片,然后如果需要的话,再加上5000张来自手机上传的图片。然后对于开发集和测试集,这数据集的大小是按比例画的,你的开发集和测试集都是手机图。而训练集包含了来自网页的20万张图片,还有5000张来自应用的图片,开发集就是2500张来自应用的图片,测试集也是2500张来自应用的图片。这样将数据分成训练集、开发集和测试集的好处在于,现在你瞄准的目标就是你想要处理的目标,你告诉你的团队,我的开发集包含的数据全部来自手机上传,这是你真正关心的图片分布。我们试试搭建一个学习系统,让系统在处理手机上传图片分布时效果良好。缺点在于,当然了,现在你的训练集分布和你的开发集、测试集分布并不一样。但事实证明,这样把数据分成训练、开发和测试集,在长期能给你带来更好的系统性能。我们以后会讨论一些特殊的技巧,可以处理训练集的分布和开发集和测试集分布不一样的情况。
把你真正关心的数据设成你的开发和测试集。让你的训练集数据来自和开发集、测试集不同的分布,这样你就可以有更多的训练数据。在这些样本中,这将改善你的学习算法。
数据分布不匹配时,偏差与方差的分析
估计学习算法的偏差和方差真的可以帮你确定接下来应该优先做的方向,但是,当你的训练集来自和开发集、测试集不同分布时,分析偏差和方差的方式可能不一样,我们来看为什么。
我们继续用猫分类器为例,我们说人类在这个任务上能做到几乎完美,所以贝叶斯错误率或者说贝叶斯最优错误率,我们知道这个问题里几乎是0%。所以要进行错误率分析,你通常需要看训练误差,也要看看开发集的误差。比如说,在这个样本中,你的训练集误差是1%,你的开发集误差是10%,如果你的开发集来自和训练集一样的分布,你可能会说,这里存在很大的方差问题,你的算法不能很好的从训练集出发泛化,它处理训练集很好,但处理开发集就突然间效果很差了。但如果你的训练数据和开发数据来自不同的分布,你就不能再放心下这个结论了。
所以这个分析的问题在于,当你看训练误差,再看开发误差,有两件事变了。首先算法只见过训练集数据,没见过开发集数据。第二,开发集数据来自不同的分布。而且因为你同时改变了两件事情,很难确认这增加的9%误差率有多少是因为算法没看到开发集中的数据导致的,这是问题方差的部分,有多少是因为开发集数据就是不一样。
为了分辨清楚两个因素的影响,定义一组新的数据是有意义的,我们称之为训练-开发集,所以这是一个新的数据子集。我们应该从训练集的分布里挖出来,但你不会用来训练你的网络。
我们要做的是随机打散训练集,然后分出一部分训练集作为训练-开发集(training-dev),就像开发集和测试集来自同一分布,训练集、训练-开发集也来自同一分布。但不同的地方是,现在你只在训练集训练你的神经网络,你不会让神经网络在训练-开发集上跑后向传播。为了进行误差分析,你应该做的是看看分类器在训练集上的误差,训练-开发集上的误差,还有开发集上的误差。
比如说这个样本中,训练误差是1%,我们说训练-开发集上的误差是9%,然后开发集误差是10%,和以前一样。你就可以从这里得到结论,当你从训练数据变到训练-开发集数据时,错误率真的上升了很多。而训练数据和训练-开发数据的差异在于,你的神经网络能看到第一部分数据并直接在上面做了训练,但没有在训练-开发集上直接训练,这就告诉你,算法存在方差问题,因为训练-开发集的错误率是在和训练集来自同一分布的数据中测得的。所以你知道,尽管你的神经网络在训练集中表现良好,但无法泛化到来自相同分布的训练-开发集里,它无法很好地泛化推广到来自同一分布,但以前没见过的数据中,所以在这个样本中我们确实有一个方差问题。
我们来看一个不同的样本,假设训练误差为1%,训练-开发误差为1.5%,但当你开始处理开发集时,错误率上升到10%。现在你的方差问题就很小了,因为当你从见过的训练数据转到训练-开发集数据,神经网络还没有看到的数据,错误率只上升了一点点。但当你转到开发集时,错误率就大大上升了,所以这是数据不匹配的问题。因为你的学习算法没有直接在训练-开发集或者开发集训练过,但是这两个数据集来自不同的分布。但不管算法在学习什么,它在训练-开发集上做的很好,但开发集上做的不好,所以总之你的算法擅长处理和你关心的数据不同的分布,我们称之为数据不匹配的问题。
如果我们说训练误差是10%,训练-开发误差是11%,开发误差为12%,要记住,人类水平对贝叶斯错误率的估计大概是0%,如果你得到了这种等级的表现,那就真的存在偏差问题了。存在可避免偏差问题,因为算法做的比人类水平差很多,所以这里的偏差真的很高。
最后一个例子,如果你的训练集错误率是10%,你的训练-开发错误率是11%,开发错误率是20%,那么这其实有两个问题。第一,可避免偏差相当高,因为你在训练集上都没有做得很好,而人类能做到接近0%错误率,但你的算法在训练集上错误率为10%。这里方差似乎很小,但数据不匹配问题很大。所以对于这个样本,我说,如果你有很大的偏差或者可避免偏差问题,还有数据不匹配问题。
所以我们讲了如何使用来自和开发集、测试集不同分布的训练数据,这可以给你提供更多训练数据,因此有助于提高你的学习算法的性能,但是,潜在问题就不只是偏差和方差问题,这样做会引入第三个潜在问题,数据不匹配。如果你做了错误分析,并发现数据不匹配是大量错误的来源,那么你怎么解决这个问题呢?但结果很不幸,并没有特别系统的方法去解决数据不匹配问题,但你可以做一些尝试,可能会有帮助,我们来看下一段视频。
处理数据不匹配问题
如果您的训练集来自和开发测试集不同的分布,如果错误分析显示你有一个数据不匹配的问题该怎么办?这个问题没有完全系统的解决方案,但我们可以看看一些可以尝试的事情。如果我发现有严重的数据不匹配问题,我通常会亲自做错误分析,尝试了解训练集和开发测试集的具体差异。技术上,为了避免对测试集过拟合,要做错误分析,你应该人工去看开发集而不是测试集。
但作为一个具体的例子,如果你正在开发一个语音激活的后视镜应用,你可能要看看……我想如果是语音的话,你可能要听一下来自开发集的样本,尝试弄清楚开发集和训练集到底有什么不同。所以,比如说你可能会发现很多开发集样本噪音很多,有很多汽车噪音,这是你的开发集和训练集差异之一。也许你还会发现其他错误,比如在你的车子里的语言激活后视镜,你发现它可能经常识别错误街道号码,因为那里有很多导航请求都有街道地址,所以得到正确的街道号码真的很重要。当你了解开发集误差的性质时,你就知道,开发集有可能跟训练集不同或者更难识别,那么你可以尝试把训练数据变得更像开发集一点,或者,你也可以**收集更多类似你的开发集和测试集的数据。**所以,比如说,如果你发现车辆背景噪音是主要的错误来源,那么你可以模拟车辆噪声数据,我会在下一张幻灯片里详细讨论这个问题。或者你发现很难识别街道号码,也许你可以有意识地收集更多人们说数字的音频数据,加到你的训练集里。可以一起尝试收集更多和真正重要的场合相似的数据,这通常有助于解决很多问题。
如果你的目标是让训练数据更接近你的开发集,那么你可以怎么做呢?
你可以利用的其中一种技术是人工合成数据(artificial data synthesis),我们讨论一下。在解决汽车噪音问题的场合,所以要建立语音识别系统。也许实际上你没那么多实际在汽车背景噪音下录得的音频,或者在高速公路背景噪音下录得的音频。但我们发现,你可以合成。所以假设你录制