C语言每日一练 —— 第22天：零基础学习动态规划

一、前言

    之前的文章中，我有讲过一些经典的动态规划，例如：最长单调子序列、最长公共子序列、最小编辑距离、背包问题、记忆化搜索、区间DP、数位DP，其中不乏一些较难的内容，不太好理解，所以这篇文章，我会对基础的动态规划再做一个梳理，从最简单的线性DP开始讲起，来谈谈零基础如何一步一步搞清楚动态规划。
    点击文末【阅读原文】可跳转到视频讲解。

二、递推

    首先让我们来看一下，零基础学习动态规划前必须要看的一道题。

1、斐波那契数列

1）题目描述

    给定一个 $n(0\le n\le 30)$，求斐波那契数列的第 $n$ 项。

2）算法分析

    斐波那契数列就是一个从 $0$ 和 $1$ 开始，其后每一项都等于前两项的和，就像这样：
$$\begin{gathered} F(0)=0 \\ F(1)=1 \\ F(n)=F(n-1)+F(n-2)，其中n>1 \end{gathered}$$

    拿到这个题目，我们首先来看题目范围，$n$ 最多不超过 30，那是因为斐波那契数的增长速度很快，是指数级别的。所以如果 $n$ 很大，就会超过 c语言 中32位整型的范围。这是一个最基础的递推题，递推公式都已经告诉你了，我们要做的就是利用一个循环来实现这个递推。

3）源码详解

int fib(int n) {
    int i;                      // (1)
    int f[31] = {0, 1};         // (2)
    for(i = 2; i <= n; ++i) {   // (3)
        f[i] = f[i-1] + f[i-2]; // (4)
    }
    return f[n];                // (5)
}

• $(1)$ 首先定义一个循环变量；
• $(2)$ 再定义一个数组记录斐波那契数列的第 $n$ 项，并且初始化第 $0$ 项 和 第 $1$ 项。
• $(3)$ 然后一个 for 循环，从第 2 项开始；
• $(4)$ 利用递推公式逐步计算每一项的值；
• $(5)$ 最后返回第 $n$ 项即可。

4）简单复盘

    递推其实是一种最简单的状态转移，如果对状态的概念还比较模糊，没有关系。接下来的内容，我会不断给你灌输状态的概念，接下来让我们来看另一道题，它是斐波那契数列的简单应用。

2、爬楼梯

1）题目描述

    给定一个 $n(1\le n\le 45)$ 代表总共有 $n$ 阶楼梯，一开始在第 $0$ 阶，每次可以爬 $1$ 或者 $2$ 个台阶，问总共有多少种不同的方法可以爬到楼顶。

2）算法分析

    我们定义一个数组 $f[46]$，其中 $f[i]$ 表示从第 $0$ 阶爬到第 $i$ 阶的方案数。

    由于每次可以爬 $1$ 或者 $2$ 个台阶，所以对于第 $i$ 阶楼梯来说，所以要么是从第 $i-1$ 阶爬过来的，要么是从 $i-2$ 阶爬过来的，如图所示：

    于是得出一个递推公式
$$f[i]=f[i-1]+f[i-2]$$
    我们发现这个就是斐波那契数列，你可以叫它递推公式，也可以叫它状态转移方程。这里的 $f[i]$ 就是状态的概念，从一个状态到另一个状态就叫状态转移。
    当然我们还要考虑初始状态，$f[0]$ 代表从第 $0$ 阶到第 $0$ 阶的方案数，当然就是 $1$ 啦，$f[1]$ 代表从第 $0$ 阶到第 $1$ 阶的方案数，由于只能走 $1$ 阶，所以方案数也是 $1$。

3）源码详解

int climbStairs(int n){
    int i;                      // (1)
    int f[46] = {1, 1};         // (2)
    for(i = 2; i <= n; ++i) {   // (3)
        f[i] = f[i-1] + f[i-2]; // (4)
    }
    return f[n];                // (5)
}

• $(1)$ 首先定义一个循环变量；
• $(2)$ 再定义一个数组 $f[i]$ 代表从第 $0$ 阶爬到第 $i$ 阶的方案数；
• $(3)$ 然后一个 for 循环，从第 2 项开始；
• $(4)$ 利用递推公式逐步计算每一项的值；
• $(5)$ 最后返回第 $n$ 项即可。

4）简单复盘

    通过这道题我们发现，一个问题可以有不同的问法，但是最后解法是相同的。如何把复杂的问题转换成我们学过的内容就是抽象问题的能力，抽象这个词很抽象，需要不断的练习才能领悟其中的精髓。

三、线性DP

    递推也是某种意义上的线性DP，线性DP的最大特征就是状态是用一个一维数组表示的，一般状态转移的时间复杂度为 $O(1)$ 或者 $O(n)$。
    让我们来看一个线性DP的经典例子来加深理解。

1、使用最小花费爬楼梯

1）题目描述

    给定一个 $n(n\le 1000)$，再给定一个 $n$ 个整数的数组 $cost$， 其中 $cost[i]$ 是从楼梯第 $i$ 个台阶向上爬需要支付的费用。一旦支付此费用，即可选择向上爬一个或者两个台阶。
    可以选择从下标为 $0$ 或下标为 $1$ 的台阶开始爬楼梯，请计算并返回达到楼梯顶部的最低花费。

2）算法分析

    我们发现这题和之前的爬楼梯很像，只不过从原来的计算方案数变成了计算最小花费。
    我们尝试用一个数组来表示状态：$f[i]$ 表示爬到第 $i$ 层的最小花费。

由于每次只能爬 $1$ 个或者 $2$ 个台阶，所以 $f[i]$ 这个状态只能从 $f[i-1]$ 或者 $f[i-2]$ 转移过来：
    1）如果从 $i-1$ 爬上来，需要的花费就是 $f[i-1]+cost[i-1]$；
    2）如果从 $i-2$ 爬上来，需要的花费就是 $f[i-2]+cost[i-2]$；
    没有其他情况了，而我们要 求的是最小花费，所以 $f[i]$ 就应该是这两者的小者，得出状态转移方程：
$$f[i]=min(f[i-1]+cost[i-1],f[i-2]+cost[i-2])$$
    然后考虑一下初始情况 $f[0]$ 和 $f[1]$，根据题目要求它们都应该是 0。

3）源码详解

int min(int a, int b) {
    return a < b ? a : b;                   // (1)
}

int minCostClimbingStairs(int* cost, int n){
    int i;                                  // (2)
    int f[1001] = {0, 0};                   // (3)
    for(i = 2; i <= n; ++i) {               // (4)
        f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2]);
    }
    return f[n];                            // (5)
}

• $(1)$ 为了方便求最小值，我们实现一个最小值函数 $min$，直接利用 C语言 的 条件运算符 就可以了；
• $(2)$ 然后开始动态规划的求解，首先定义一个循环变量；
• $(3)$ 再定义一个数组 $f[i]$ 代表从第 $0$ 阶爬到第 $i$ 阶的最小花费，并且初始化第 $0$ 项 和 第 $1$ 项；
• $(4)$ 然后一个for循环，从第 $2$ 项开始，直接套上状态转移方程就能计算每一项的值了；
• $(5)$ 最后返回第 $n$ 项即可；

4）简单复盘

    这道只是最简单的动态规划入门题，比较简单，越简单我们就越能总结出规律。通过做这三道题，我们可以总结出刷动态规划题的大致流程：
    1、设计状态
    2、写出状态转移方程
    3、设定初始状态
    4、执行状态转移
    5、返回最终的解

    让我们尝试做一道进阶题找找感觉。

2、打家劫舍

1）题目描述

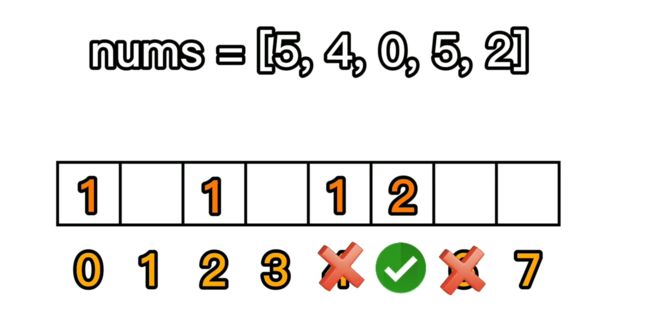
    给定一个整数 $n(1\le n\le 100)$，再给定一个 $n$ 个整数的数组 $nums$，每个整数可以选择取或者不取，如果第 $i$ 个整数取，那么 第 $i-1$ 或者 $i+1$ 个整数就不能取。

    要求按照上述规则选取一些整数，使得选出来的整数得到的总和最大，返回这个最大值。

2）算法分析

    对于 $n$ 个整数而言，每个整数可以选择取或者不取，所以总共有 $2^n$ 次种取法。但是相邻的数不能都取，所以方案数是小于 $2^n$ 次的。然而可以预见还是指数级别的嘛，所以暴力枚举肯定会超时的。
    所以我们定义一个状态数组 $dp[i]$，表示前 $i$ 个整数通过某种选取方案能够获得的最大值。
    1）如果第 $i$ 个整数不取，那么第 $i-1$ 有取和不取两种情况，于是转换成了 $dp[i-1]$ 的子问题；

    2）如果第 $i$ 个整数取，那么第 $i-1$ 个肯定不能取，但是 第 $i-2$ 个整数有取和不取两种情况，于是转换成了 $dp[i-2]$ 的子问题。

    所以状态转移方程如下：
$$dp[i]=max(dp[i-1],dp[i-2]+nums[i])$$
    然后我们来看初始状态，就是以第 $0$ 个元素结尾的最大值。当然就是这样啦：
$$dp[0]=nums[0]$$
    当然为了防止数组下标越界，以第 $1$ 个元素结尾的最大值也需要求出来：
$$dp[1]=max(nums[0],nums[1])$$

3）源码详解

int max(int a, int b) {
    return a > b ? a : b;            // (1)
}

int rob(int* nums, int n){
    int i;                           // (2)
    int dp[110];
    dp[0] = nums[0];                 // (3)
    for(i = 1; i < n; ++i) {         // (4)
        if(i == 1) {                 // (5)
            dp[1] = max(nums[0], nums[1]);
        }else {                      // (6)
            dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
        }
    }
    return dp[n-1];                  // (7)
}

• $(1)$ 首先要求的是最大值，所以我们用条件运算符简单实现一个求最大值的函数；
• $(2)$ 然后开始动态规划的求解，首先定义一个循环变量；
• $(3)$ 定义一个状态数组 $dp[i]$，初始状态 $dp[0]$ 为 $nums[0]$；
• $(4)$ 然后一层循环执行状态转移；
• $(5)$ 为了防止调用 $dp[i-2]$ 时的数组下标越界，当 i == 1的情况需要特殊处理，也比较简单啦，就是要么取第 0 个要么取第 1 个；
• $(6)$ 当 i > 1时直接套用刚才研究出来的状态转移方程就可以啦；
• $(7)$ 最后返回 $dp[n-1]$ 就是我们要求的答案了；

4）简单复盘

    这个题是一个基础线性DP题，和爬楼梯基本是如出一辙。之所以叫线性是因为状态数和时间复杂度呈线性关系，是 O(n) 的。
    每个状态的状态转移的时间复杂度是 $O(1)$，那么什么是 $O(1)$ 呢？简单理解就是状态转移的时间与 $n$ 无关，这道题目中无论 $n$ 多大，$i$ 的状态一定是从 $i-1$ 或者 $i-2$ 转移过来的，所以每次状态转移最多两次计算。$O(1)$ 的含义更多的是代表常数时间复杂度。

3、删除并获得点数

1）题目描述

    给定一个整数 $n(1\le n\le 10^5)$，再给定 $n$ 个不超过 $10^4$ 的整数组成的数组 $nums$， 每个整数可以选择取或者不取。如果 $x$ 取，那么将会获得 $x$ 个点数，取完以后必须删除所有值为 $x-1$ 和 $x+1$ 的整数。
    要求按照上述规则选取一些整数，使得选出来的整数得到的总和最大，返回这个最大值。

2）算法分析

    对于这个问题，我们可以发现整数的范围不超过 $10000$，利用好这个条件是成功解题的关键。由于数字不大，所以我们可以把所有数字都映射到数组里，然后某个数字取了以后相邻的数字不能取，咦？？？这不就是打家劫舍那道题嘛。

3）源码详解

int max(int a, int b) {
    return a > b ? a : b;
}

int rob(int* nums, int n){
    int i;
    int dp[10010];
    dp[0] = nums[0];
    for(i = 1; i < n; ++i) {
        if(i == 1) {
            dp[1] = max(nums[0], nums[1]);
        }else {
            dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
        }
    }
    return dp[n-1];
}

int deleteAndEarn(int* nums, int n){
    int i;                         // (1)
    int sum[10010], val[10010];    // (2)
    memset(sum, 0, sizeof(sum));   // (3)
    for(i = 0; i < n; ++i) {
        ++sum[ nums[i] ];          // (4)
    }
    for(i = 0; i <= 10000; ++i) {
        val[i] = i * sum[i];       // (5)
    }
    return rob(val, 10001);        // (6)
}

• $(1)$ 首先定义一个循环变量；
• $(2)$ 然后定义两个辅助数组 $sum[i]$ 和 $val[i]$， 后面我会解释它们的作用。
• $(3)$ 将 $sum$ 数组利用 $memset$ 归零；
• $(4)$ 一层循环将所有数字映射到 $sum$ 数组中，$sum[i]$ 的值代表的是 $i$ 在数组中的个数；
• $(5)$ 然后填充 $val[i]$，$val[i]$ 的值代表选取 $i$ 这个数以后能够获得的点数，当然就是它本身的值乘上它的个数，即 $i\times sum[i]$；
• $(6)$ 然后直接把 打家劫舍的代码拷过来，修改一下数组范围，直接调用即可；

4）简单复盘

    这个问题，需要一点闹经急转弯，当然这里也存在经验的成分，看到数字范围小于 $10^6$，基本就要想一下是否能够映射到数组下标，从而把问题转换成我们学过的问题。

4、最大子数组和

1）题目描述

    给定一个整数 $n(1\le n\le 10^5)$，再给定一个 $n$ 个整数的数组 $nums$，请找出一个具有 最大和的连续子数组，返回其最大和。

2）算法分析

    对于 $n$ 个整数，总共有多少个子数组呢？我们可以枚举起点、枚举终点，总共有 $n\ast (n+1)/2$ 个子数组，如果枚举所有子数组，并且再对所有子数组求和取最大值，总共有三个 $for$ 循环，时间复杂度是 $O(n^3)$，对于 $10^5$ 的数量级，这个时间复杂度明显是不能接受的。让我们利用动态规划的套路，回忆一下动态规划的刷题流程：
    1、设计状态
    2、写出状态转移方程
    3、设定初始状态
    4、执行状态转移
    5、返回最终的解

    所以我们定义一个状态数组 $dp[i]$ 表示以第 $i$ 个整数结尾的子数组中的最大值，以第 $i$ 个整数结尾的子数组分为两种情况：
    1、和第 $i-1$ 个整数结尾的子数组相连；
    2、和第 $i-1$ 个整数结尾的子数组不相连（就是起点和终点都是第 $i$ 个整数的情况）；
    这两种情况取大者就是我们要求的解，所以我们可以得出状态转移方程如下
$$dp[i]=max(dp[i-1]+nums[i],nums[i])$$
    然后我们来看初始状态，就是以第 $0$ 个元素结尾的最大值，当然就是这样啦
$$dp[0]=nums[0]$$

3）源码详解

int max(int a, int b) {
    return a > b ? a : b;               // (1)
}

int maxSubArray(int* nums, int n){
    int i;                              // (2)
    int dp[100001];                     // (3)
    int maxValue = nums[0];             // (4)
    dp[0] = nums[0];                    // (5)
    for(i = 1; i < n; ++i) {            // (6)
        dp[i] = max(dp[i-1] + nums[i], nums[i]);
        maxValue = max(maxValue, dp[i]);// (7)
    }
    return maxValue;                    // (8)
}

• $(1)$ 定义一个求最大值的函数；
• $(2)$ 定义一个循环变量；
• $(3)$ 定义一个状态数组 $dp[i]$ ；
• $(4)$ 定义一个我们要返回的最大值，初始化为第一个整数的值；
• $(5)$ 计算初始状态 $dp[0]$；
• $(6)$ 利用一层循环，执行状态转移；
• $(7)$ 然后在所有以第 $i$ 个整数结尾的子数组中取一个最大值；
• $(8)$ 最后返回这个最大值就是我们要求的答案了；

4）简单复盘

    这道题显然和前面的题难度有所增加，可以多看几遍，多想想，利用所有的碎片时间来进行学习，迟早会想出来的，那么好好想想吧，祝你好运！

四、总结复盘

1、状态

    如果你学过编译原理，那么你应该会知道 DFA （有限状态自动机），没错，这里的状态就可以理解成状态机中的状态，即 DFA 上的某个结点。

2、状态转移

    状态转移则对应了 DFA 上的边，即从一个状态到另一个状态，边上也有可能有条件，也就对应了状态转移的条件。

3、时间复杂度

    动态规划的时间复杂度分为两部分：状态计算的时间复杂度，每个状态的状态转移时间复杂度。
    所有状态计算的时间复杂度为 $O(a)$，单个状态的状态转移时间复杂度为 $O(b)$，则整个动态规划的求解过程的时间复杂度就是 $O(ab)$。
    线性DP 的状态数就是 $O(n)$，状态转移的时间复杂度一般为 $O(1)$ 或者 $O(n)$，也有 $O(lo{g}_{2}n)$ 的，可能利用二分枚举进行状态转移，比如最长单调子序列。

4、线性DP拓展

    常见的线性DP有最长单调子序列、前缀最值、前缀和、背包问题等等。

5、刷题路线

    可以通过公众号 「 夜深人静写算法 」 回复「 题集 」 获取。