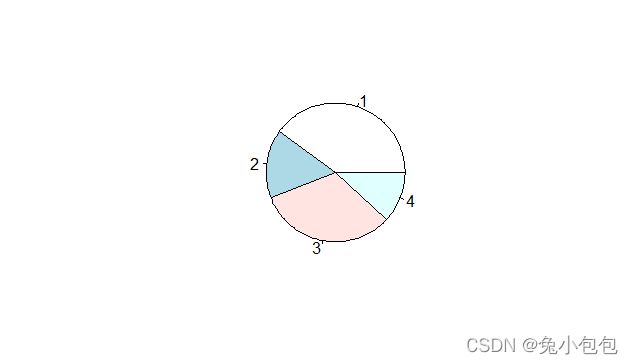R数据分析：方法与案例详解--自学笔记

@[TOC] (目录）

第二章 数据结构与基本运算

2.1 数据类型

数值型（numeric）

整数
小数
科学数

字符型（character）

== 夹杂单引号或者双引号之间==“MR”

逻辑型

==只能读取T （TRUE）或 F (FALSE)值

复数型

a+bi

原始型（raw）

以二进制形式保存数据

默认值（missing value）

不可得到（not available）或 缺失值（missing value）时，相关位置可能会被保留并且赋予一个特定的NA
任何NA的运算结果都是NA
is.na()函数用来检测数据是否缺失

2.2 数据对象

向量（vector）

向量赋值

由有相同基本类型元素组成的序列，相当于一维数组
单个向量中的数据要求必须是相同类型，同一向量中无法混杂不同类型的数据

赋值方法：<-;=;->;assign

assign(“w”,c(1,2,3,4,5))
w
[1] 1 2 3 4 5

用c( )构建向量

v<-paste(“x”,1:5,sep="")
v
[1] “x1” “x2” “x3” “x4” “x5”
paste("today is ",date())
[1] “today is Sun Nov 21 10:14:20 2021”
对于字符向量，一个很重要的函数paste（）可以把自变量对应元素连成一个字符串，长度不想相同时，较短的向量会被重复使用

向量运算

对应向量的每个分量做乘法、除法和乘方运算

x<-c(1,3,5,7,9)
c(1,3,5,7,9)->y
x*y
[1] 1 9 25 49 81
x/y
[1] 1 1 1 1 1
x^2
[1] 1 9 25 49 81
y^x
[1] 1 27 3125 823543 387420489

整数除法

5%/%3
[1] 1

求余数

5%%3
[1] 2

向量运算会对该向量的每一个元素进行同样的运算出现在同一个表达式的向量最好统一长度。如果长度不一，则表达式中短的向量会被循环使用，表达式的值将是一个和最长的向量等长的向量。

c(1,3,5)+c(2,4,6,7,10)
[1] 3 7 11 8 13
Warning message:
In c(1, 3, 5) + c(2, 4, 6, 7, 10) : 长的对象长度不是短的对象长度的整倍数

生成有规则序列

R可以产生正规则序列，最简单的是用“：”符号，就可以产生有规律的正规则序列。

(t<-1:10)
[1] 1 2 3 4 5 6 7 8 9 10
(r<-5:1)
[1] 5 4 3 2 1
2*1:5
[1] 2 4 6 8 10
在表达式运算中，：的运算级别最高
在表达式外面套（）的意思是把结果直接打印出来，不套括号则运算结果保存在t对象里
t<-1:10
t
[1] 1 2 3 4 5 6 7 8 9 10

可以用seq（）产生有规律的各种序列seq（from，to，by）

seq(1,10,2)
[1] 1 3 5 7 9
seq(1,10)
[1] 1 2 3 4 5 6 7 8 9 10
seq(10,1,-1)
[1] 10 9 8 7 6 5 4 3 2 1

关注序列的长度

seq(1,2,length=10)
[1] 1.000000 1.111111 1.222222 1.333333 1.444444 1.555556
[7] 1.666667 1.777778 1.888889 2.000000
seq(1,by=2,length=10)
[1] 1 3 5 7 9 11 13 15 17 19

用各种复杂的方式重复一个对象rep（x，times，…）

rep(c(1,3),4)
[1] 1 3 1 3 1 3 1 3
rep(c(1,3),each=4)
[1] 1 1 1 1 3 3 3 3
rep(1:3,rep(2,3)) rep()的嵌套使用里层的rep（1,3）等价于向量（2，2，2）
[1] 1 1 2 2 3 3

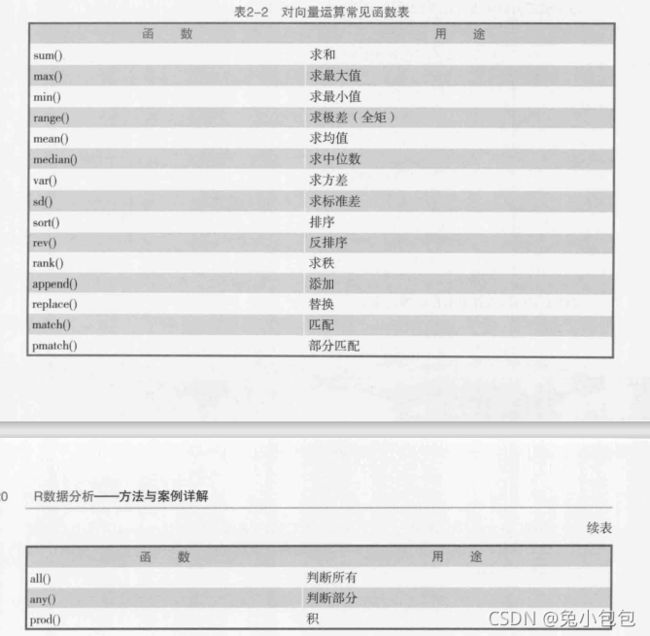
向量的常见函数

向量里元素的个数称为向量的长度（length）。长度为1的向量就是常数（或标量）。函数length（）可以返回向量的长度，mode（）可以返回向量的数据类型，min（）返回向量的最小值，range（）返回向量的范围，which.min(）、which.max（）返回在第几个分量求到最小值和最大值。

x<-c(1,2,3,4,5)
length(x)
[1] 5
mode(x)
[1] “numeric”
min(x)
[1] 1
range(x)
[1] 1 5
which.min(x)
[1] 1

内置函数可以直接对向量进行运算：mean（）求均值，median（）求中位数，var（）求方差，sd（）求标准差。

t<-1:10
mean(t)
[1] 5.5
sd(t)
[1] 3.02765
sort（）对向量排序，rev（）将向量按原方向的反方向排列，rank（）给出向量的秩，prod（）求向量的连乘积，append（）为向量添加元素。
y<-c(2,6,7,3,5)
sort(y)
[1] 2 3 5 6 7
rev(y)
[1] 5 3 7 6 2
rank(y)
[1] 1 4 5 2 3
prod(y)
[1] 1260
append(y,10:15,after = 3)
[1] 2 6 7 10 11 12 13 14 15 3 5

向量索引

向量下标运算：取出向量的某一个元素既可以用x[i]得出，也可以通过赋值语句来改变一个或多个元素的值。

x<-c(1,3,5)
x[2]
[1] 3
(c(1,2,3)+4)[2]
[1] 6
x[2]<-10
x
[1] 1 10 5
x[c(1,3)]<-c(9,11)
x
[1] 9 10 11

对向量进行逻辑运算

x<-c(1,3,5)
x<4
[1] TRUE TRUE FALSE
x[x<4]
[1] 1 3
z<-c(-1,1:3,NA)
z
[1] -1 1 2 3 NA
z[is.na(z)]<-0
z
[1] -1 1 2 3 0
z<-c(-1,1:3,NA)
y<-z[!is.na(z)]
y
[1] -1 1 2 3

对分段函数的定义上

x<-c(-3,-2,-1,0,5,7)
y<-numeric(length(x)) #生成与x向量长度相同的数值型向量
y
[1] 0 0 0 0 0 0
y[x<0]<-1-x[x<0]
y
[1] 4 3 2 0 0 0
y[x>=0]<-1+x[x>=0]
y
[1] 4 3 2 1 6 8

如果下标取的是负整数，则表示删除相应位置的元素

x<-1:10
x[-(1:5)]
[1] 6 7 8 9 10

矩阵

将数据用行和列排列的长方形表格，是二维数组，其单元必须是相同的数据类型。通常用列来表示通的变量，用行表示各个对象。
matrix（data=NA,nrow=1,ncol=1,byrow=FALSE, dimnames=NULL）

matrix(1:12,nrow=4,ncol=3)
[,1] [,2] [,3]
[1,] 1 5 9
[2,] 2 6 10
[3,] 3 7 11
[4,] 4 8 12
matrix(1:12,nrow=4,ncol=3,byrow=T)
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
[4,] 10 11 12
假定A为一个m*n矩阵，则A的转置可以用函数t（）来计算。
类似的若将函数t（）作用于一个向量x，则当做x为列向量，返回结果为一个行向量；若想得到一个列向量，可用t（t（x））
(A<-matrix(1:12,nrow=4,ncol=3))
[,1] [,2] [,3]
[1,] 1 5 9
[2,] 2 6 10
[3,] 3 7 11
[4,] 4 8 12
t(A)
[,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 5 6 7 8
[3,] 9 10 11 12

矩阵计算

A<-B<-matrix(1:12,nrow=3)
A+B
[,1] [,2] [,3] [,4]
[1,] 2 8 14 20
[2,] 4 10 16 22
[3,] 6 12 18 24
3*A
[,1] [,2] [,3] [,4]
[1,] 3 12 21 30
[2,] 6 15 24 33
[3,] 9 18 27 36

B<-t(A)
A%*%B
[,1] [,2] [,3]
[1,] 166 188 210
[2,] 188 214 240
[3,] 210 240 270

取一个方阵的对角元素

A<-matrix(1:16,nrow=4)
diag(A)
[1] 1 6 11 16
diag(diag(A)) 对向量应用
[,1] [,2] [,3] [,4]
[1,] 1 0 0 0
[2,] 0 6 0 0
[3,] 0 0 11 0
[4,] 0 0 0 16
diag(3)
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1

求逆

(A<-matrix(rnorm(16),4,4))
[,1] [,2] [,3] [,4]
[1,] 0.6301784 2.4225384 0.5726452 -0.03666071
[2,] -0.5308961 -0.1890815 0.8882178 0.25320483
[3,] -0.3427778 0.1166931 0.1330065 -2.33152019
[4,] 1.0215506 1.0354465 -1.2353513 2.08501209
solve(A)
[,1] [,2] [,3] [,4]
[1,] 1.04091346 -4.1951340 -3.02955246 -2.8599709
[2,] -0.01396465 1.3982578 1.15670814 1.1234135
[3,] 0.65240603 -1.2592565 -1.56038581 -1.5804721
[4,] -0.11651514 0.6149107 -0.01462486 0.3865359

数组

既可以看做是带有多个下标的且类型相同的元素的集合，也可以看做是向量和矩阵的推广，一维数组就是向量，二维数组就是矩阵。
array（data=NA,dim=length(data）,dimnames=NULL)

(xx<-array(1:24,c(3,4,2)))
, , 1

 [,1] [,2] [,3] [,4]

[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12

, , 2

 [,1] [,2] [,3] [,4]

[1,] 13 16 19 22
[2,] 14 17 20 23
[3,] 15 18 21 24

xx[2,3,2]
[1] 20
xx[2,1:3,2]
[1] 14 17 20
xx[,2,]
[,1] [,2]
[1,] 4 16
[2,] 5 17
[3,] 6 18
dim(xx)
[1] 3 4 2

dim()可以用来将向量换成数组或矩阵

zz=c(2,5,6,8,1,4,6,9,10,7,3,5)
dim(zz)=c(2,2,3)
zz
, , 1

 [,1] [,2]

[1,] 2 6
[2,] 5 8

, , 2

 [,1] [,2]

[1,] 1 6
[2,] 4 9

, , 3

 [,1] [,2]

[1,] 10 3
[2,] 7 5

因子

分类型数据经常要把数据分成不同的水平或因子，如学生的性别包含男和女两个因子。因子代表变量的不同可能水平（即使在数据中不出现），在统计分析中十分有用。
factor（x=character（），levels，labels=levels，exclude=NA，ordered=is.ordered（x））

y<-c(“女”,“男”,“男”,“女”,“女”,“女”,“男”)
(f<-factor(y))
[1] \u5973 \u7537 \u7537 \u5973 \u5973 \u5973 \u7537
Levels: \u7537 \u5973

score<-c(“B”,“C”,“D”,“B”,“A”,“D”,“A”)
(score_o<-ordered(score,levels=c(“D”,“C”,“B”,“A”)))
[1] B C D B A D A
Levels: D < C < B < A

列表

如果一个数据对象需要含有不同的数据类型，则可以采用列表。列表中包含的对象又称为它的分量，分量可以是不同的模式或类型，如一个列表可以包含数值向量、逻辑向量、矩阵、字符和数组等。
list（变量1=分量1，变量2=分量2，…）

x<-c(1,1,2,2,3,3,3)
y<-c(“女”,“男”,“男”,“女”,“女”,“女”,“男”)
z<-c(80,85,92,76,61,95,83)
(LST<-list(class=x,sex=y,score=z))
$class
[1] 1 1 2 2 3 3 3

$sex
[1] “\u5973” “\u7537” “\u7537” “\u5973” “\u5973” “\u5973”
[7] “\u7537”

$score
[1] 80 85 92 76 61 95 83
==注意LST[[]]和LST[]的差别

LST[[3]]
[1] 80 85 92 76 61 95 83
LST[[2]][1:3]
[1] “\u5973” “\u7537” “\u7537”

LST$score[1]80859276619583LST$sc
[1] 80 85 92 76 61 95 83

函数length（）、mode（）、names（）可以返回列表的长度（分量的书目）、数据类型和列表里成分的名字。

数据框

数据库是一种矩阵形式的数据，但数据框中各列可以是不同类型的数据。数据框每列是一个变量，每行是一个观测。数据框既可以看做是矩阵的推广，也可以看做是一种特殊的列表对象。

data.frame(…, row.names=NULL, check.rows=FALSE,…)

(student<-data.frame(x,y,z))
x y z
1 1 \u5973 80
2 1 \u7537 85
3 2 \u7537 92
4 2 \u5973 76
5 3 \u5973 61
6 3 \u5973 95
7 3 \u7537 83
(student<-data.frame(class=x,sex=y,score=z)) #对列进行重新命名
class sex score
1 1 \u5973 80
2 1 \u7537 85
3 2 \u7537 92
4 2 \u5973 76
5 3 \u5973 61
6 3 \u5973 95
7 3 \u7537 83
row.names(student)<-c(“王”,“张”,“赵”,“刘”,“黄”,“孙”,“李”) #对行进行重新命名
student
class sex score
\u738b 1 \u5973 80
\u5f20 1 \u7537 85
\u8d75 2 \u7537 92
\u5218 2 \u5973 76
\u9ec4 3 \u5973 61
\u5b59 3 \u5973 95
\u674e 3 \u7537 83

以数组形式访问

student[, “score”]
[1] 80 85 92 76 61 95 83
student[,3]
[1] 80 85 92 76 61 95 83
student[1:5,1:3]
class sex score
\u738b 1 \u5973 80
\u5f20 1 \u7537 85
\u8d75 2 \u7537 92
\u5218 2 \u5973 76
\u9ec4 3 \u5973 61

以列表形式访问数据框

student$score[1]80859276619583student[["score"]][1]80859276619583student[[3]][1]80859276619583student[student$score>80,]
class sex score
\u5f20 1 \u7537 85
\u8d75 2 \u7537 92
\u5b59 3 \u5973 95
\u674e 3 \u7537 83

数据框绑定attach（）函数

数据框的主要用途是保存统计建模的数据。在使用数据框的变量时可以使用“数据框名$变量名的记法”。但是这样较为麻烦，attach（）函数可以把数据框中的变量“链接”到内存中，将数据框“绑定”入当前的名字空间，从而可以直接用数据中的变量名访问。

第三章 函数与优化

3.2条件控制语句

if/else语句

if（cond）statement-1
if（cond）statement-1 else statement-2

x<-1.5
if(x>2) y=2x else y=3x
y
[1] 4.5
x<-3
if(x>2) y=2x else y=3x
y
[1] 6

ifelse语句

ifelse（cond，statement1，statement2）

x<-1
ifelse(x>2,y<-2x,y<-3x)
[1] 3

switch语句

switch（statement，list）
如果表达式的返回值在1到length（list）之间，则返回列表相应位置的值

switch(1,23,sd(1:5),runif(3)) #返回23,sd(1:5),runif(3)list中的第一个成分
[1] 6
switch(2,23,sd(1:5),runif(3)) #返回第二个成分
[1] 1.581139
switch(3,23,sd(1:5),runif(3))
[1] 0.7357111 0.8724102 0.2977454
当list是有名定义，statement等于变量名时，返回变量名对应的值；否则返回NULL值。
x<-“meat”
switch(x,meat=“chicken”,fruit=“apple”,vegetable=“potato”)
[1] “chicken”

3.3循环语句

for循环

for （ind in expr-1）expr-2

Fibonacci<-NULL
Fibonacci[1]<-Fibonacci[2]<-1
n=16
for (i in 3:n) Fibonacci[i]<-Fibonacci[i-2]+Fibonacci[i-1]
Fibonacci
[1] 1 1 2 3 5 8 13 21 34 55 89 144 233 377
[15] 610 987

while

while（condition）expr

Fibonacci[1]<-Fibonacci[2]<-1
i<-1
while (Fibonacci[i]+Fibonacci[i+1]<1000) {

•    Fibonacci[i+2]<-Fibonacci[i]+Fibonacci[i+1]
  

•    i<-i+1     }
  

Fibonacci
[1] 1 1 2 3 5 8 13 21 34 55 89 144 233 377
[15] 610 987

repeat语句

repeat expr
repeat循环依赖break语句跳出循环

Fibonacci[1]<-Fibonacci[2]<-1
i<-1
repeat {Fibonacci[i+2]<-Fibonacci[i]+Fibonacci[i+1]

•     i<-i+1
  

•     if (Fibonacci[i]+Fibonacci[i+1]>=1000) break}
  

Fibonacci
[1] 1 1 2 3 5 8 13 21 34 55 89 144 233 377
[15] 610 987

编写自己的函数

函数名=function（参数1，参数2…）
{
stataments
return(object)
}

函数名

函数名可以是任何值，但以前定义过的要小心使用，后来定义的函数会覆盖原先定义的函数。一旦你定义了函数名，就可以像使用R的其他函数一样使用它。

std=function(x) sqrt(var(x))
x=c(1,3,5,7,9)
std(x)
[1] 3.162278
std
function(x) sqrt(var(x))

关键词function

告诉R这个新的数据对象是函数

参数

1无参数：有时编写参数只是为了方便，函数每次返回值都是一样的，其输入不是那么重要。

welcome=function() print(“welcome to use R”)
welcome()
[1] “welcome to use R”

2单参数：假如要使你的函数个性化，则可以使用单参数，函数会根据参数的不同，返回值也不同。

welcome.sb=function(names) print(paste(“welcome”, names,“to use R”))
welcome.sb(“Mr fang”)
[1] “welcome Mr fang to use R”

3默认参数：即不输入任何参数

welcome.sb=function(names=“Mr fang”) print(paste(“welcome”, names,“to use R”))
welcome.sb()
[1] “welcome Mr fang to use R”

sim.t=function(n) {

• mu=10;sigma=5;
• x=rnorm(n,mu,sigma)
• (mean(x)-mu)/(sd(x)/sqrt(n))
• }

sim.t(5)
[1] 0.8751291

sim.t=function(n,mu=10,sigma=5) {

• x=rnorm(n,mu,sigma)
• (mean(x)-mu)/(sd(x)/sqrt(n))
• }

sim.t(5)
[1] 0.4513926
sim.t(5,0,1)
[1] -0.7608016
sim.t(5,4)
[1] -0.5832039
sim.t(5,sigma = 100)
[1] 1.175098
sim.t(5,sigma=100,mu=1)
[1] -0.6865917

R语言允许定义一个变量，然后将变量值传递给R的内置函数。这在作图上非常有用。比如编写一个画图函数，允许先定义一个变量x，再用这个变量生成y变量，然后描出他们的图像。

plot.f=function(f,a,b,…){

• xvals=seq(a,b,length=100)
• plot(xvals,f(xvals),…)
• }

plot.f(sin,0,2pi)
curve(sin,0,2pi)
plot.f(exp,-1,1)
plot.f(log,0,1)

函数体和函数返回值

my.averange=function(x) sum(x)/length(x)
my.averange(c(1,2,3))
[1] 2

当函数体的表达式超过一个时，要用{}封起来
可以用return（）返回函数需要的结果，当需要返回多个结果时，一般建议用list形式返回。

vms=function(x) {

• xx=rev(sort(x))
• xx=xx[1:5]
• mean(xx)
• return(list(xbar=mean(xx),top5=xx))
• }

y=c(5,15,32,25,26,28,65,48,3,37,45,54,23,44)
vms(y)
$xbar
[1] 51.2

$top5
[1] 65 54 48 45 44

程序调试

程序运行时间与效率

用R做优化求解

一元函数优化求解

f=function(x) log(x)-x^2
curve(f,xlim = c(0,2))
optimize(f,c(0.1,10),tol=0.0001,maximum = T)
$maximum
[1] 0.7071232

$objective
[1] -0.8465736

第四章 随机数与抽样模拟

4.1一元随机数的产生

均匀分布随机数

runif（n，min，max=1）

runif(3,1,3)
[1] 1.679771 2.910882 2.381824
runif(5) # 默认生成5个【0,1】上的均匀分布随机数
[1] 0.9988105 0.6044897 0.5033955 0.4804998 0.4007253

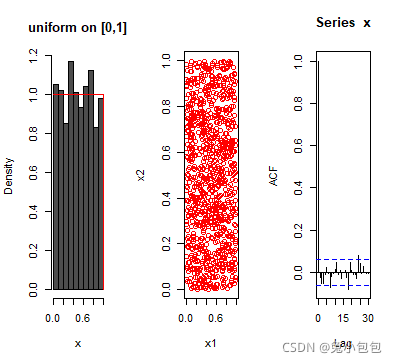
检验runif（）生成的随机数的性质，通过直方图和散点图以及自相关系数图来检验独立同分布。

x=runif(Nsim)
x1=x[-Nsim] #因为要求自相关系数，去掉最后一个数
x2=x[-1] #去掉第一个数
par(mfrow=c(1,3))
hist(x,prob=T,col=gray(0.3),main=“uniform on [0,1]”)
curve(dunif(x,0,1),add=T,col=“red”)
plot(x1,x2,col=“red”)
acf(x) #画自相关系数图

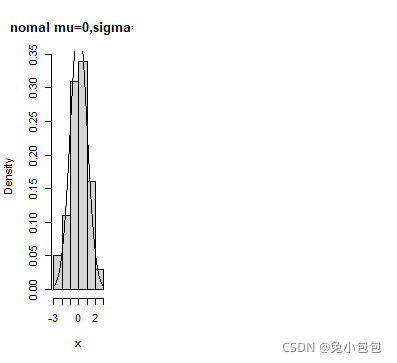
正态分布随机数

rnorm（n，mean=0，sd=1）

rnorm(5,10,5)
[1] -4.586236 7.835159 9.310051 16.012151 8.246510
rnorm(5)
[1] 0.3259324 0.9488270 -1.5844309 -0.8577230
[5] -1.4327578

x=rnorm(100)
hist(x,prob=T,main=“nomal mu=0,sigma=1”)
curve(dnorm(x),add=T)

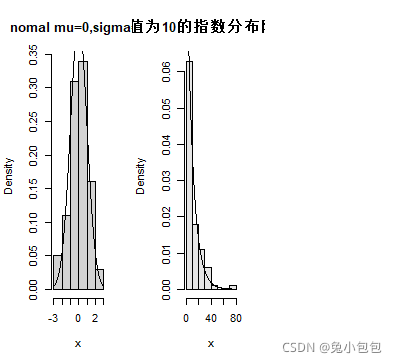
指数分布随机数

rexp（n，lamda=1）

x=rexp(100,1/10)
hist(x,prob=T,col=gray(0.9),main=“均值为10的指数分布随机数”)
curve(dexp(x,1/10),add=T)

离散分布随机数的生成

rbinom(10,size,p)
[1] 0 0 1 1 1 0 1 1 1 1

size=10;p=0.5
rbinom(5,size,p)
[1] 3 4 3 6 6

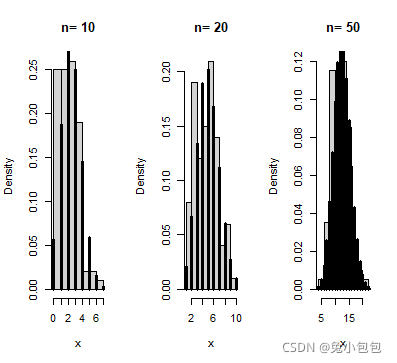
par(mfrow=c(1,3))
p=0.25
for (n in c(10,20,50))

• {x=rbinom(100,n,p)
• hist(x,prob=T,main=paste(“n=”,n))
• xvals=0:n
• points(xvals,dbinom(xvals,n,p),type=“h”,lwd=3)
• }

par(mfrow=c(1,1))

4.2多元随机数的生成

4.3随机抽样

放回与无放回抽样

R可以进行有放回、无放回抽样。
sample（x，n，replace=F，prob=NULL）
x表示总体向量，可以是数值、字符、逻辑向量，n表示样本容量，replace=F表示无放回的抽样（默认），prob可以设置各个抽样单元不同的入样概率，进行不等概率抽样。

sample(1:6,10,rep=T)
[1] 3 4 5 5 4 4 5 2 4 6
sample(c(“H”,“T”),10,rep=T)
[1] “T” “T” “T” “H” “H” “T” “T” “H” “T” “H”

sample(1:6,10,rep=T)
[1] 5 1 4 3 3 1 5 4 3 6
dice=as.vector(outer(1:6,1:6,paste))
sample(dice,5,replace=T)
[1] “5 4” “4 2” “5 5” “2 1” “2 6”
dice=as.vector(outer(1:6,1:6,paste))
dice
[1] “1 1” “2 1” “3 1” “4 1” “5 1” “6 1” “1 2” “2 2”
[9] “3 2” “4 2” “5 2” “6 2” “1 3” “2 3” “3 3” “4 3”
[17] “5 3” “6 3” “1 4” “2 4” “3 4” “4 4” “5 4” “6 4”
[25] “1 5” “2 5” “3 5” “4 5” “5 5” “6 5” “1 6” “2 6”
[33] “3 6” “4 6” “5 6” “6 6”

bootstrap重抽样

属于重复抽样（Resampling）方法。它是以原始数据为基础的模拟抽样统计推断法，其基本思想是;在原始数据的范围内做有放回的再抽样，样本量仍为n，原始数据中每个观察单位每次被抽到的概率相等，为1/n。

faithful
eruptions waiting
1 3.600 79
2 1.800 54
attach(faithful)
sample(eruptions,10,replace=T)
[1] 2.000 4.000 4.483 1.833 1.750 2.000 1.800 3.850 2.083 2.217

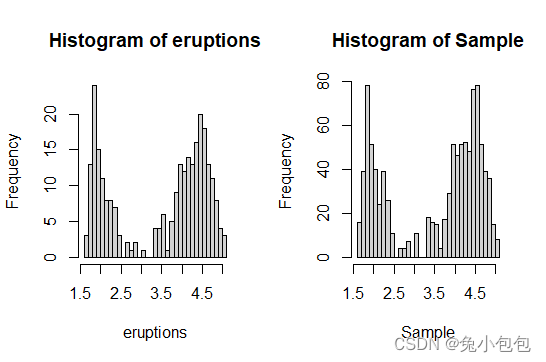
Sample=sample(eruptions,1000,rep=T)
par(mfrow=c(1,2))
hist(eruptions,breaks = 25)
hist(Sample,breaks = 25)
par(mfrow=c(1,1))

4.4统计模拟

几种常见的模拟方法

第五章 数据读写与预处理

5.1数据的读入

直接输入数据

1.c（）函数
把各个值连成一个向量或列表，可以形成数值型向量、字符型向量或者其他类型向量

2.scan（）函数
类似c（）函数，是一种键盘输入数据函数，当输入scan（）并按回车键后，将等待输入数据，数据之间只用空格分开即可（c（）函数要用逗号分开）。输入完成后，再次按回车键，这是数据录入完毕。

x=scan()
1: 1 2 3 4 5 6
7:
Read 6 items

还可以读入外部文本文件
x=scan(file=“dat.txt”)
如果原文件的数据之间有逗号等分隔符，则用scan（）函数读入时应该去掉这些分隔符：
x=scan(file=“dat.txt”, sep=",")

读R包中的数据

在RStudio中，虽然可以直接查看、读取和修改数据，但有一些操作还是需要使用命令来运行。例如，查看当前环境下的数据ls（）、删除数据rm（）、查看所有预先提供的数据data（）、查看某个包所有预先提供的数据data（package=“”）或读入数据data（datasetname）。
如果需要从其他的软件包链接数据，则可以使用参数package。

data(package=“SemiPar”) #查看包的信息
data(copper,package=“SemiPar”) #查看包里的某个数据

从外部文件读入数据

1.读入文本文件
read.table(file,header = logical_value,sep=“delimiter”,row.names = “name”)

2.读入Excel数据
对于一般常用的xls、xlsx数据表，由于该格式较为复杂，因此应尽量避免直接导入。通常的处理办法是将xls数据表转为CSV文件。
read.csv(“file=file.name”,header=TRUE,sep=",",…)

s2=read.csv(file=“student-1.csv”)
s2
class sex score
1 1 女 80
2 1 男 85
3 2 男 92
4 2 女 76
5 3 女 61
6 3 女 95
7 3 男 83

3.读入其他数据格式
library(foreign)
①sas数据
对于sas，R只能读入sas transport format（XPORT）文件。所以，需要把普通的sas数据文件（.ssd和.sas7bdat）转换为transport format（XPORT）文件，再用命令read.xport().
read.xport(“dataname.xpt”)
②spss数据
read.spss()可读入spss数据文件。
==read.spss(“dataname.sav”)==或
install.packages(“Hmmisc”)
library(Hmmisc)
mydataframe<-spss.get(“dataname.sav”,use.value.labels=TRUE)
③Epi info数据
R可读入epi5和6的数据库。
read.epiinfo(“文件名.rec”)
给数据集起一个名称：read.epiinfo(“d:/ttt.rec”)->ttt
④stata数据
R可读入stata5，7和6的数据库。
read.dta(“文件名.dta”)

读入数据文件后，使用数据集名$变量名，既可以使用各个变量。mean（data$age）
便是计算数据集data中变量age的均数。

5.2写出数据

write(x,file=“data”,ncolumns=if(is.character(x)) 1 else 5,append=FALSE,sep=" ")
write.table(x,file=" “,append=FALSE,quote=TRUE,sep=” “,eol=”\n",na=“NA”,dec=".",row.names=TRUE,col.names=TRUE,qmethod=c(“escape”,“double”),fileEncoding=" ")
write.csv()

5.3数据预处理

变量预处理

1创建新变量
var_names=expr
读入数据

cons<-c(5000,5800,6000,10200,8500)
pop<-c(2000,3600,3500,5020,6100)
gnp<-c(6000,7200,7400,11000,9200)

直接进行变换

pgnp<-gnp/pop
psave<-(gnp-cons)/pop

用transform（）函数进行变换。
> data<-data.frame(gnp,cons,pop)

transform(data,pgnp=gnp/pop,psave=(gnp-cons)/pop )
gnp cons pop pgnp psave
1 6000 5000 2000 3.000000 0.5000000
2 7200 5800 3600 2.000000 0.3888889
3 7400 6000 3500 2.114286 0.4000000
4 11000 10200 5020 2.191235 0.1593625
5 9200 8500 6100 1.508197 0.1147541

用with（）函数进行变换。

(pgnp<-with(data,gnp/pop ))
[1] 3.000000 2.000000 2.114286 2.191235 1.508197
(psave<-with(data,(gnp-cons)/pop))
[1] 0.5000000 0.3888889 0.4000000 0.1593625 0.1147541

变量重编码

①将连续性变量进行分组，变成一个离散型变量
②将某个值替换成另外一个值

data(Cars93)
dat<-data.frame(manu=Cars93$Manufacturer,price=Cars93$Price)
head(dat)
manu price
1 Acura 15.9
2 Acura 33.9
3 Audi 29.1
4 Audi 37.7
5 BMW 30.0
6 Buick 15.7

利用【】将price分成不同的取值区间

dat$pricegrade<-NAdat$pricegrade[dat$price>=20]<-"expensive"dat$pricegrade[datKaTeX parse error: Expected 'EOF', got '&' at position 10: price>=12&̲datprice<20]<-“okay”
dat$pricegrade[dat$price<12]<-“cheap”
head(dat)
manu price pricegrade
1 Acura 15.9 okay
2 Acura 33.9 expensive
3 Audi 29.1 expensive
4 Audi 37.7 expensive
5 BMW 30.0 expensive
6 Buick 15.7 okay

使用within（）函数

dat<-within(dat,{

• pricegrade<-NA
• pricegrade[price>=20]<-“expensive”
• pricegrade[price>=12&dat$price<20]<-“okay”
• pricegrade[price<12]<-“cheap”
• })

head(dat)
manu price pricegrade
1 Acura 15.9 okay
2 Acura 33.9 expensive
3 Audi 29.1 expensive
4 Audi 37.7 expensive
5 BMW 30.0 expensive
6 Buick 15.7 okay

使用cut（）函数

dat$pricegrade<-cut(dat$price,c(0,12,20,max(dat$price)))levels(dat$pricegrade)<-c(“cheap”,“okay”,“expensive”)
head(dat)
manu price pricegrade
1 Acura 15.9 okay
2 Acura 33.9 expensive
3 Audi 29.1 expensive
4 Audi 37.7 expensive
5 BMW 30.0 expensive
6 Buick 15.7 okay

将数据直接替换

recode(dat$pricegrade,"‘cheap’=‘A’;‘okay’=‘B’;‘expensive’=‘C’")
[1] B C C C C B C C C C C B A B B B B B C B B C A A B B
[27] B C B B A A A B B B C C A B B B B A A A B C C C C C
[53] A A B B C C C B B A C A B B C B B B C B A A B B C C
[79] A A A B A A B B C A B B C C C
Levels: A B C

变量重命名

一使用交互式编辑器
在命令窗口输入fix（data），会自动调用一个交互式的编辑器，单击变量名，然后在弹出的对话框中将其重命名。
fix(data)

二reshape包中有rename（）函数，可用于修改变量名
dat1 <- rename(dat, c(pricegrade=“grade”))
head(dat1)

三直接通过names（）函数来重命名变量

names(dat)[3] <- “grade”
head(dat)
manu price grade
1 Acura 15.9 okay
2 Acura 33.9 expensive
3 Audi 29.1 expensive
4 Audi 37.7 expensive
5 BMW 30.0 expensive
6 Buick 15.7 okay

变量类型的转换

a <- c(1,2,3);
a
[1] 1 2 3
is.numeric(a)
[1] TRUE
is.vector(a)
[1] TRUE
a <- as.character(a);
a
[1] “1” “2” “3”
is.numeric(a)
[1] FALSE
is.vector(a)
[1] TRUE
is.character(a)
[1] TRUE

日期变量的转换

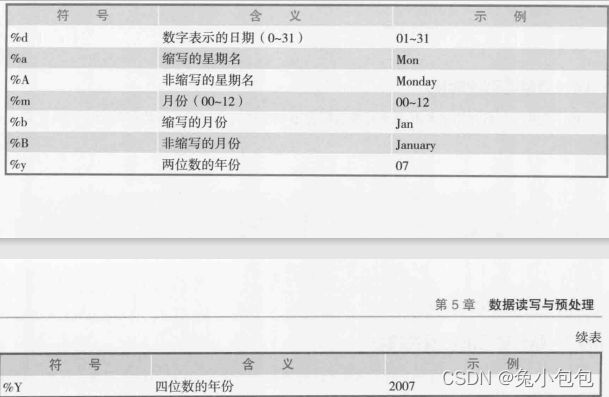
日期值通常以字符串的形式输入到R中，然后转化为数值形式存储的日期变量。函数as.Date()用于执行这种转化。
==as.Date(x,“input_format”),其中x是字符型数据，input——format则给出了用于读入日期的适当格式。

madates <- as.Date(c(“2010-06-22”, “2013-09-14”))
(madates <- as.Date(c(“2010-06-22”, “2013-09-14”)))
[1] “2010-06-22” “2013-09-14”
日期的默认输入格式为yyyy-mm-dd
strDates <- c(“01/05/1965”, “08/16/1975”)
dates <- as.Date(strDates, “%m/%d/%Y”)
dates
[1] “1965-01-05” “1975-08-16”

5.4缺失数据处理

完全随机缺失：数据的缺失是随机的，数据的缺失不依赖任何完全变量或完全变量。缺失情况相对于所有可观测和不可观测的数据来说，在统计意义上是独立的。
随机缺失：数据的缺失不是完全随机的，依赖于其他变量，即一个观测出现缺失值的概率是由数据集中不含缺失值的变量决定的，而不是由含缺失值的变量决定的。
完全非随机缺失：数据的缺失依赖于不完全变量自身，是与缺失数据本身存在某种关联，比如问题设计过于敏感造成的缺失。

缺失数据的识别

缺失值用符号NA表示。
dataframe$age[dataframe$age == 99] <- NA
在进行数据分析前，要确保所有的缺失数据被编码为缺失值，否则分析结果将失去意义。

缺失数据的探索与检验

R提供了一些函数，用于识别包含缺失值的观测。函数is.na()检测缺失值是否存在。

y<-c(1,2,3,NA)
is.na(y)
[1] FALSE FALSE FALSE TRUE

函数complete.cases() 可用来识别矩阵或者数据框中没有缺失值的行。若每行都包含完整的实例，则返回TRUE；若每行有一个或多个缺失值，则返回FALSE。由于逻辑值TRUE和FALSE分别等价于数值1和0，可用sum() 和mean() 来获取关于缺失数据有用的信息。

data(sleep, package= “VIM”) #读取VIM包中的sleep数据
sleep[!complete.cases(sleep),] #提取sleep数据中不完整的行

sum(!complete.cases(sleep))
[1] 20
mean(complete.cases(sleep))
[1] 0.6774194

结果列出了20个含有一个或多个缺失值的观测值，并有67.7%的完整实例。

缺失数据的处理

（1）行删除：可以通过函数 na.omit() 移除所有含有缺失值的观测。na.omit() 可以删除所有含有缺失数据的行。

newsleep <- na.omit(sleep)
sleep[!complete.cases(newsleep),]
[1] BodyWgt BrainWgt NonD Dream Sleep Span
[7] Gest Pred Exp Danger
<0 行> (或0-长度的row.names)

删除缺失值后，观测值变为42个。
行删除法假定数据是MCAR（即完整的观测值只是全数据集的一个随机样本）。此例中则为42个实例为62个样本的一个随机子样本。
如果缺失值所占比例比较小的话, 这一方法十分有效。然而, 这种方法却有很大的局限性。它是以减少样本量来换取信息的完备, 会造成资源的大量浪费, 丢弃了大量隐藏在这些对象中的信息。在样本量较小的情况下, 删除少量对象就足以严重影响到数据的客观性和结果的正确性。因此, 当缺失数据所占比例较大, 特别是当缺失数据非随机分布时, 这种方法可能导致数据发生偏离, 从而得出错误的结论。

（2）均值替换法（Mean Imputation）：我们将变量的属性分为数值型和非数值型来分别进行处理。如果缺失值是数值型的, 就根据该变量在其他所有对象的取值的平均值来填充该缺失的变量值; 如果缺失值是非数值型的, 就根据统计学中的众数原理, 用该变量在其他所有对象的取值次数最多的值来补齐该缺失的变量值。
均值替换法也是一种简便、快速的缺失数据处理方法。使用均值替换法插补缺失数据, 对该变量的均值估计不会产生影响。
但这种方法是建立在完全随机缺失( MCAR ) 的假设之上的, 而且会造成变量的方差和标准差变小。同时，这种方法会产生有偏估计, 所以并不被推崇。

（3）多重插补（Multiple Imputation）：在面对复杂的缺失值问题时，MI是最常用的方法，它将从一个包含缺失值的数据集中生成一组完整的数据集。每个模拟的数据集中，缺失数据将用蒙特卡洛方法来填补。由于多重估算技术并不是用单一的值来替换缺失值, 而是试图产生缺失值的一个随机样本, 这种方法反映出了由于数据缺失而导致的不确定，R中的mice包可以用来执行这一操作。
基于mice包的分析通常按照以下过程分析：
library(mice)
imp <- mice(data, m)
fit <- with(imp, analysis)
pooled <- pool(fit)
summary(pooled)
其中，imp是一个包含m个插补数据集的列表对象，同时还含有完成插补过程的信息。默认m值为5。
analysis是一个表达式对象，用来设定应用于m个插补数据集的统计分析方法，例如线性回归模型的lm()函数、广义线性模型的glm()函数，做广义可加模型的gam()等。
fit是一个包含m个单独统计分析结果的列表对象。
pooled是一个包含这m个统计分析平均结果的列表对象。
library(mice)
data(sleep,package=“VIM”)
imp<-mice(sleep,seed=6666)
fit<-with(imp,lm(Dream~Span+Gest))
pooled<-pool(fit)
summary(pooled)

5.5数据集的合并与拆分

数据框的合并与拆分

有时如果希望分组进行统计分析，或者只分析其中的一部分数据，则可以通过拆分数据集来加以分析，有时又希望把不同组的数据合并起来分析。数据框的拆分与合并是一个互逆的过程。R里拆分数据框和合并数据框很简单，分别用函数unstack( )、stack( )。

data(“PlantGrowth”)
PlantGrowth
weight group
1 4.17 ctrl
2 5.58 ctrl
3 5.18 ctrl
4 6.11 ctrl
27 4.92 trt2
28 6.15 trt2
29 5.80 trt2
30 5.26 trt2
unPG<-unstack(PlantGrowth)
unPG
ctrl trt1 trt2
1 4.17 4.81 6.31
2 5.58 4.17 5.12
3 5.18 4.41 5.54
4 6.11 3.59 5.50
5 4.50 5.87 5.37
6 4.61 3.83 5.29
7 5.17 6.03 4.92
8 4.53 4.89 6.15
9 5.33 4.32 5.80
10 5.14 4.69 5.26
sPG=stack(unPG)
sPG
values ind
1 4.17 ctrl
2 5.58 ctrl
3 5.18 ctrl
4 6.11 ctrl
5 4.50 ctrl
6 4.61 ctrl
7 5.17 ctrl
8 4.53 ctrl
27 4.92 trt2
28 6.15 trt2
29 5.80 trt2
30 5.26 trt2

数据集的合并

要横向合并两个数据框（数据集），可以使用merge()函数。在多数情况下，两个数据框是通过一个或多个共有变量进行联结的（inner join）。例如：
newdata <- merge(dataframeA, dataframeB, by= “ID”)
将dataframeA和dataframeB按照ID进行了合并。
若要直接横向合并两个矩阵或数据框，可以直接使用cbind() 函数，为了让它正常工作，每个对象必须拥有相同的行数，且要以相同的顺序排列。
total <- cbind(A, B)

数据集的抽取

（1）保留变量：从一个大数据集中选择有限数量的变量来创建一个新的数据集。
A．newdata <- dataframe[, c(n:m)]
从dataframe数据框中选择了第n到第m个变量，将行下标留空（，）表示默认选择所有行，并将它们保存到了新的数据框newdata中。
B．vars <- c(“var1”, “var2”, “var3”, “var4” )
newdata <-dataframe[vars]

（2）剔除变量
可以使用如下语句：
A. vars <- names(dataframe) %in% c(“var1”, “var2” )
#x %in% table : 返回的是x中的每个元素是否在table中，是一个bool向量
newdata <-dataframe[!vars]
B. 在知道要删除的变量是第几个变量的情况下，可以使用语句：
newdata <- dataframe[c(-n, -m)] #删除第n和第m个变量
C. leadership$var1<-leadership$var2 <- NULL

（3）选择观测值

newdata1 <- sleep[1:20, ] #选择前20个观测
attach(sleep)
newdata2 <- sleep[which(Sleep>=3 & Sleep <6),] #选择睡眠时间在3~6小时之间的观测
detach(sleep)

（4）subset()函数

newdata3 <- subset(sleep, sleep>=3 & sleep<6, select=c(BodyWgt,Dream, Sleep,Span,Pred,Exp,Danger))
newdata4<- subset(sleep, Pred=3 & sleep<6, select=BodyWgt: Pred)
在第一个示例中，选择了所有睡眠时间在3~6小时之间的观测，且保留了BodyWgt, Dream, Sleep, Span, Pred, Exp, Danger变量。第二个示例选择了Pred为3且睡眠时间小于6小时的观测，且保留了变量BodyWgt到Pred之间的所有列。

第六章 探索性数据分析

6.1主要分析工具

探索性数据分析工具

探索性数据分析的工具包括数据的图形表示和解释。主要的图形表示方法有（括号中为R语言绘图函数）：
1．条图（barplot）：用于分类数据。
2．直方图（hist）、点图（dotchart）、茎叶图（stem）：用于观察数值型分布的形状。
3．箱线图（boxplot）：给出数值型分布的汇总数据，适用于不同分布的比较和拖尾、截尾分布的识别。
4．正态概率图（qqnorm）：用于观察数据是否近似地服从正态分布。
MS=read.csv(“mathstat.csv”)
MS

stem(MS$math)

The decimal point is 1 digit(s) to the right of the |

5 | 4
6 | 00368
7 | 003478
8 | 01134558
9 | 0135

stem(MS$stat)

The decimal point is 1 digit(s) to the right of the |

5 | 68
6 | 68
7 | 1235688
8 | 22246679
9 | 04668

茎叶图的第1位是十分位数，比如：数据成绩的茎叶图里，5|4表示有一位学生的数学成绩为54；6|00368表示有5位学生的成绩在[60,70]之间，其中两位是60分，一位63分，一位66分，一位68分，其余的类似。
从上面的茎叶图中可以看出，数学成绩和统计成绩都不完全是正态分布，如果想要知道统计成绩是否好于数学成绩，该怎么办呢？
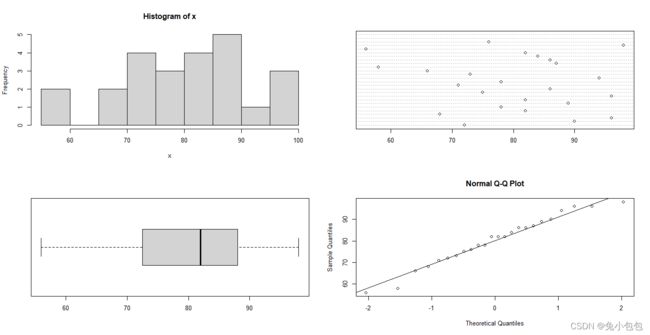
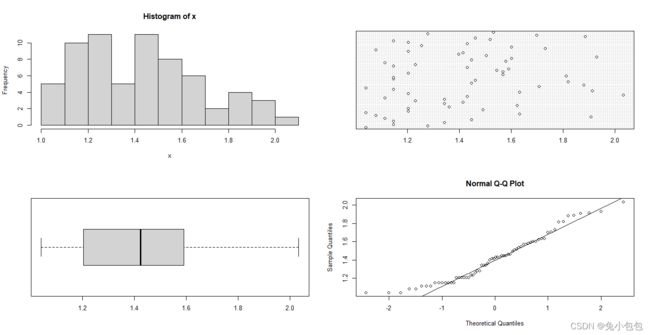
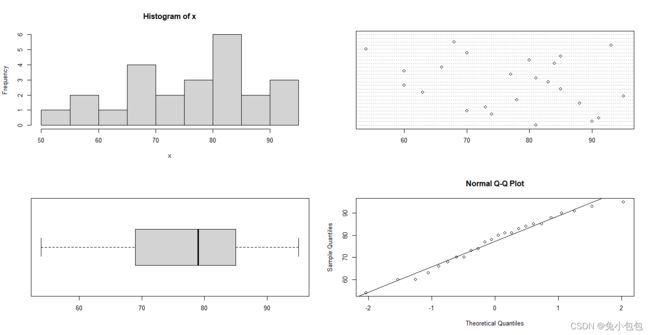
下面将一些常用的进行探索性分析的图形函数整合建立一个拥有探索性数据分析功能的函数EDA ，来对数据进行全面探索性分析：

EDA <- function (x)
{ par(mfrow=c(2,2)) # 同时做4个图（设置作图窗口为2行2列格式）
hist(x); # 直方图
dotchart(x); # 点图
boxplot(x,horizontal=T); # 箱式图，详见6.2.2
qqnorm(x);qqline(x) # 正态概率图
par(mfrow=c(1,1)) # 恢复成单图
}
EDA(MSKaTeX parse error: Expected 'EOF', got '#' at position 13: math) #̲ 探索分析数学成绩 …stat) # 探索分析统计成绩

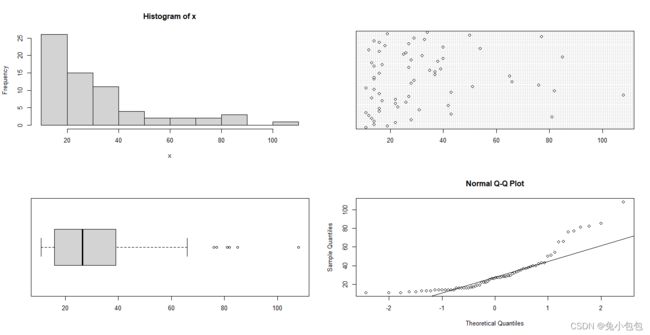
pay=c(11,19,14,22,14,28,13,81,12,43,11,16,31,16,23,42,22,26,17,22,

•   13,27,108,16,43,82,14,11,51,76,28,66,29,14,14,65,37,16,37,35,
  

•   39,27,14,17,13,38,28,40,85,32,25,26,16,12,54,40,18,27,16,14,
  

•   33,29,77,50,19,34)
  

EDA(pay)
正如所预料的那样，我们看到了一个呈严重偏态的分布。此时可以进行数据变换，可以试试对数变换（以10为底）。
log.pay =log10(pay)
EDA(log.pay)

数据的类型

   按照对客观事物测度的程度或精确水平来划分，可将数据的计量尺度从低级到高级、由粗略到精确划分为四种。

在计量尺度的应用中，需要注意的是，同类事物用不同的尺度量化，会得到不同的类别数据。如，农民收入数据按实际填写就是区间数据；按高、中、低收入水平分就是有序；按有无收入计量则是分类；而说某人的收入是另一人的两倍，便是比例数据了。再如，学生成绩按及格、不及格评定是分类；按优、良、中、及格、不及格评定是有序数据；按具体分数评定是区间数据，而平均成绩则是比例数据。
一般地，因为研究的目的和内容不同，计量尺度也会不同。如果不担心损失信息量，就可以降低度量层次。

6.2单变量数据分析

分类型数据

   统计学上把取值范围是有限个值或是一个数列构成的变量称为离散变量，其中表示分类情况的离散变量又称为分类变量。对于分类数据我们可以用频数表，条形图和饼图来描述。
   (1). 分类频数表（table）
   频数表可以描述一个分类变量的数值分布概况。R中的table命令可以生成频数表，它的使用很简单，如果x是分类数据，只要用table（x）就可以生成分类频数表。

x=c(“是”,“否”,“否”,“是”,“是”,“否”,“否”,“是”,“是”)
table(x)
x
否 是
4 5

(2). 条图（Barplot）
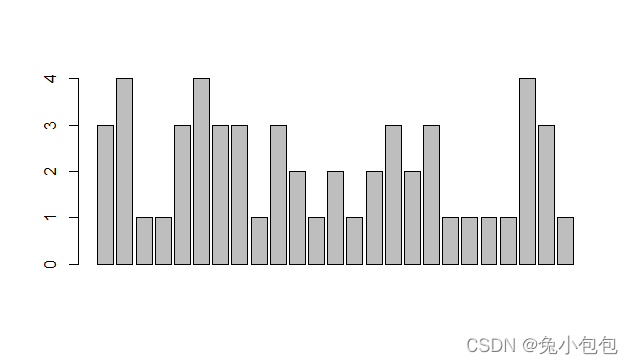
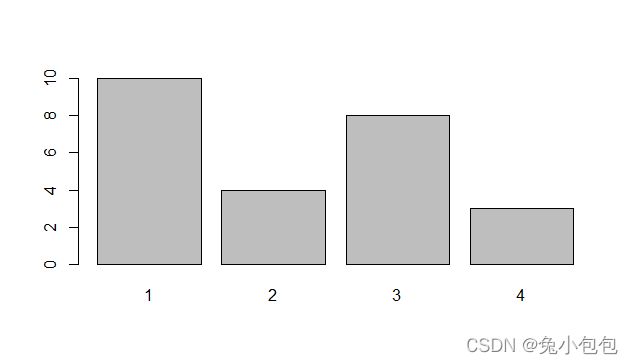
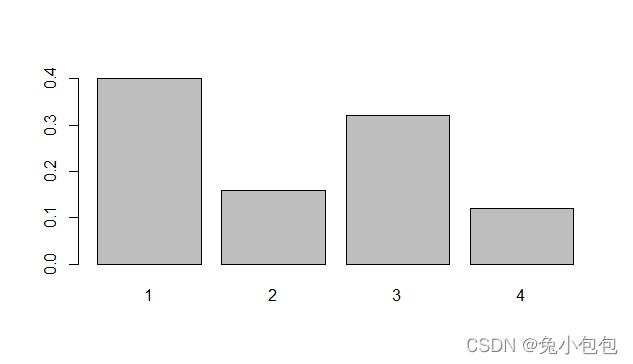
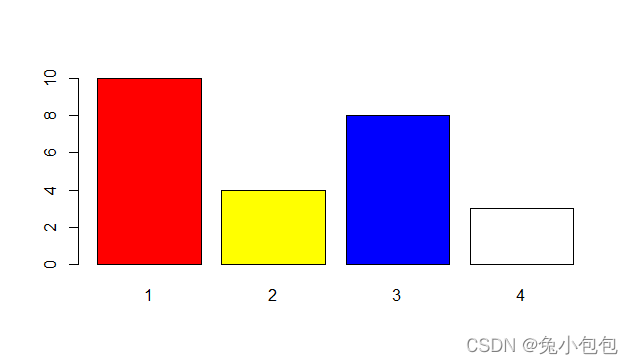
条图的高度可以是频数或频率，图的形状看起来是一样，但是刻度不一样。R画条形图的命令是barplot()。对分类数据作条形图，需先对原始数据分组，否则作出的不是分类数据的条形图。

drink=c(3, 4,1,1,3,4,3,3,1,3,2,1,2,1,2,3,2,3,1,1,1,1,4,3,1)
barplot(drink)
barplot(table(drink))

barplot(table(drink)/length(drink))
barplot(table(drink), col = c(“red”,“yellow”,“blue”,“white”))

（3). 饼图（Pie Graph）
对于分类数据还可以用饼图来描述。饼图用于表示各类别某种特征的构成比情况，它以图形的总面积为100％，扇形面积的大小表示事物内部各组成部分所占的百分比构成比。在R中作饼图也很简单，只要使用命令pie()就可以了，值得注意的一点是，像条形图一样对原始数据作饼图前要先分组。继续利用上面的饮酒者调查数据作饼图。

drink.count=table(drink) #y数据分组后赋值给drink.count。
pie(drink.count)
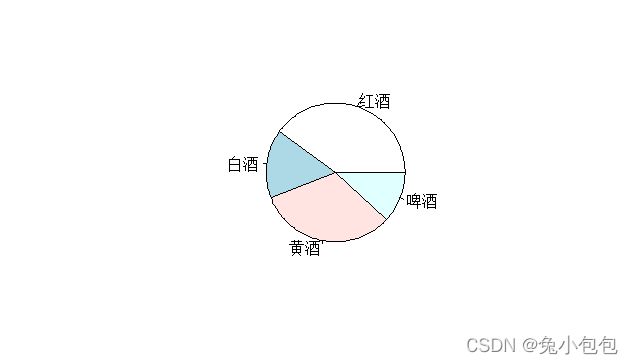
names(drink.count)=c(“红酒”,“白酒”,“黄酒”,“啤酒”)
pie(drink.count)
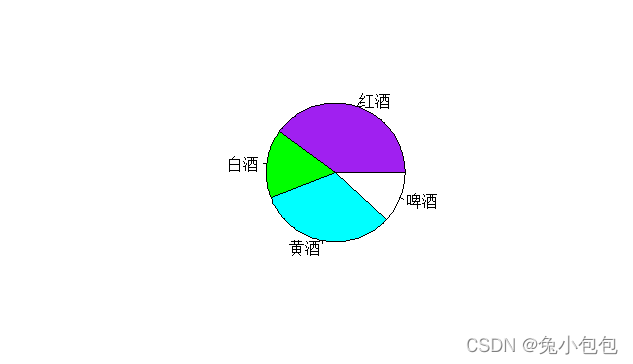
pie(drink.count,col=c(“purple”,“green”,“cyan”,“white”))

数值型数据

   (1). 集中趋势和离散程度
   对于数值型数据，经常要分析一个分布的集中趋势和离散程度，用来描述集中趋势的主要有均值，中位数；描述离散程度的主要有方差、标准差。R可以很简单地得到这些结果，只要一个命令就可以了。求均值、中位数、方差、标准差的命令分别是mean()、median()、var()、sd()。

mean(salary)
[1] 2897.368
median(salary)
[1] 2850
var(salary)
[1] 414853.8
sd(salary)
[1] 644.0915
fivenum(salary)
[1] 2000 2400 2850 3250 4200
summary(salary)
Min. 1st Qu. Median Mean 3rd Qu. Max.
2000 2400 2850 2897 3250 4200

(2). 稳健的集中趋势和离散程度
利用均值和方差描述集中趋势和离散程度往往基于正态分布，而如果数据是长尾或是有异常值时，这时用均值和方差就不能正确地描述集中趋势和离散程度。
用中位数来描述集中趋势则是稳健的，不易受异常值影响。
此外，我们还可以利用截尾均值来描述，用R计算截尾均值很简单：只要在mean函数里对trim参数进行设置就可以了。
方差、标准差对异常值也很敏感， 可以用稳健的四分位间距（IQR）和平均差(mad)来描述离散程度。

salarym=c(salary,15000)
mean(salarym,trim=0.2) #对该部门的工资截去两头20％后的均值
[1] 2870.833
mean(salarym,trim=0.5) #这是对该部门的工资截去两头50％后的均值，实际上这就是中位数
[1] 2875
IQR(salarym)
[1] 925
mad(salarym)
[1] 704.235

(3). 茎叶图（Stem-and-Leaf Graph）
由于绘制直方图时需要先对数据进行分组汇总，因此对样本量较小的情形，直方图会损失一部分信息，此时可以使用茎叶图来进行更精确的描述。茎叶图的形状与功能和直方图非常相似，但它是一种文本化的图形。R里作茎叶图很简单，只要用函数stem（）就可以了。
和直方图相比，茎叶图在反映数据整体分布趋势的同时还能够精确地反映出具体的数值大小，因此在小样本时（情况下）优势非常明显。

stem(salary)

The decimal point is 3 digit(s) to the right of the |

2 | 01234
2 | 556799
3 | 0123
3 | 58
4 | 02

stem(salarym)

The decimal point is 4 digit(s) to the right of the |

0 | 2222223333333334444
0 |
1 |
1 | 5

(4). 对数值数据分组
统计分析中经常要碰到对数值数据进行分组，在R里可以用cut函数对数值数据进行分组。

salaryg=cut(salary,breaks=c(2000,3000,4000,max(salary)))
table(salaryg)
salaryg
(2e+03,3e+03] (3e+03,4e+03] (4e+03,4.2e+03]
11 6 1

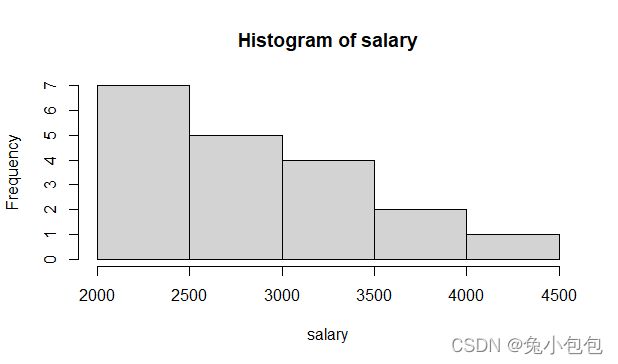
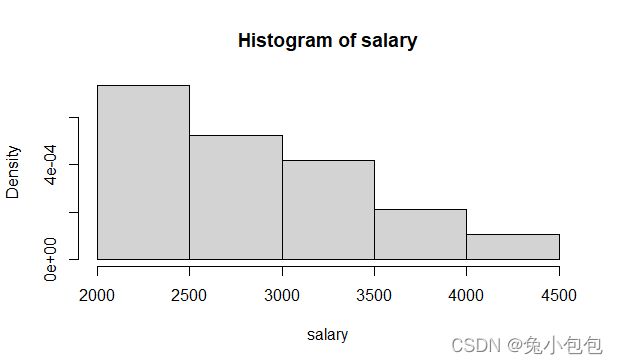
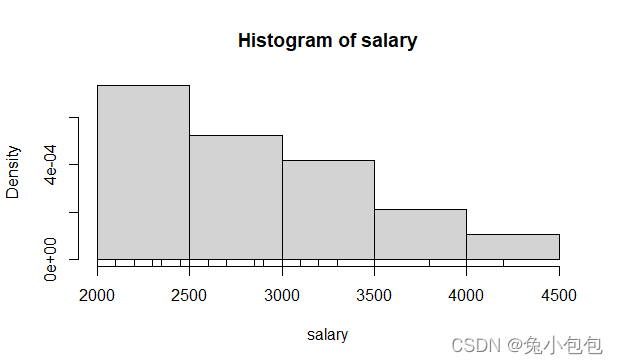
(5). 直方图（Histogram）
直方图用于表示（描述）连续性变量的频数分布，实际应用中常用于考察变量的分布是否服从某种分布类型，如正态分布。图形以矩形的面积表示各组段的频数（或频率），各矩形的面积总和为总频数（或等于1）。R里用来作（做）直方图的函数是hist()，也可以用频率作直方图，在R里作频率直方图很简单，只要把probability参数设置为T可以了，默认为F。

hist(salary)
hist(salary,prob=T)

rug(salary)

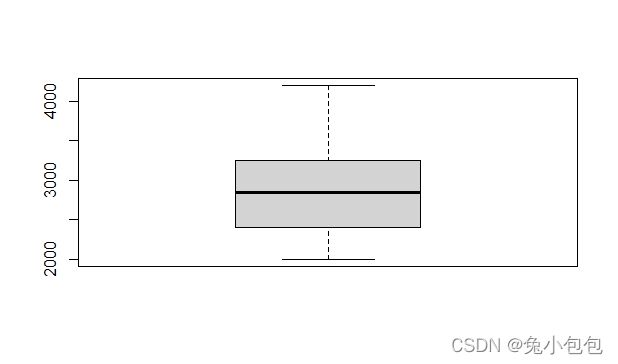
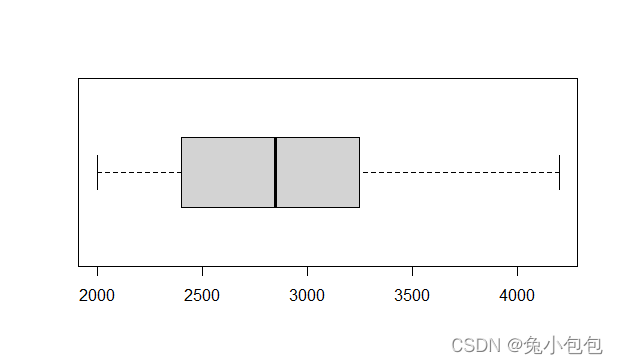
(6). 箱线图（Boxplot Graph）
箱线图是由一个箱子和两根引线构成，可分为垂直型和水平型（详见图6-12），下端引线（垂直型）或左端引线（水平型）表示数据的最小值；箱子的下端（垂直型）或左端（水平型）表示下四分位数；箱子中间的线表示中位数；箱子上端（垂直型）或右端（水平型）表示上四分位数；上端引线（垂直型）或右端引线（水平型）表示最大值。
箱线图和直方图一样都是用于考察连续变量的分布情况，但它的功能和直方图并不重叠，直方图侧重于对一个连续变量的分布情况进行详细考察，而箱线图更注重于勾勒出统计的主要信息（最小值，下四分位数，中位数、上四分位数和最大值），并且便于对多个连续变量同时考察，或者对一个变量分组进行考察，在使用上要比直方图更为灵活，用途也更为广泛。
在R里作箱线图的函数是boxplot( )，而且可以设置垂直型和水平型，默认是垂直型，要得到水平型箱线图，只要把参数horizontal设为T就可以了。

boxplot(salary)
boxplot(salary,horizontal=T)

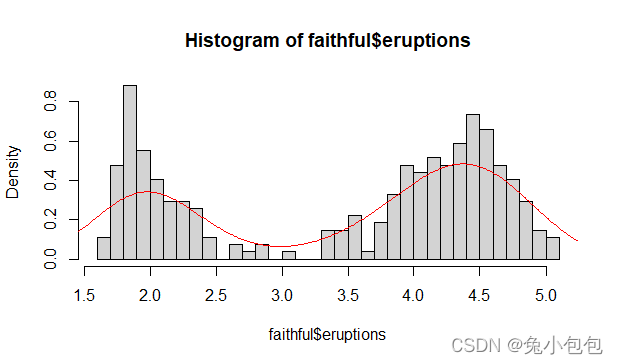
(7). 密度函数线（Densitis）
R语言里的density()函数可以画密度函数线。

hist(faithfulKaTeX parse error: Expected 'EOF', got '#' at position 30: …=T,breaks=25) #̲使用faithful数据框 l…eruptions),col=‘red’)

离群值探索

  离群值（outlier）就是某个或少数几个值明显远离于其他大部分数据。理论上讲，离群值可以出现在各种分布中，但常见的主要出现在具有测量误差（measurement error）的数据或者总体是厚尾（heavy-tailed）分布的数据中。离群值的检验主要有

箱线图
Grubb检验
Dixon’s Q检验

(1).箱线图检验
   如果观测值距箱式图底线Q1（第25百分位数）或顶线Q3（第75百分位数）过远，如超出箱体高度（四分位数间距）的1.5以上，则可视该观测值为离群值。
   boxplot.stats（）可以返回箱线图的有关统计量。
   其用法是boxplot.stats(x, coef = 1.5, do.conf = TRUE, do.out = TRUE)

返回值里，$stats是由5个值组成，第一个值是箱线图的下须线，第二个值是Q1（下四分位数），第三个是中位数，第四个是Q3（上四分位数），最后一个值是箱线图的上须线。$n返回样本量 $conf返回置信区间，默认是95的置信区间。$out返回离群值。

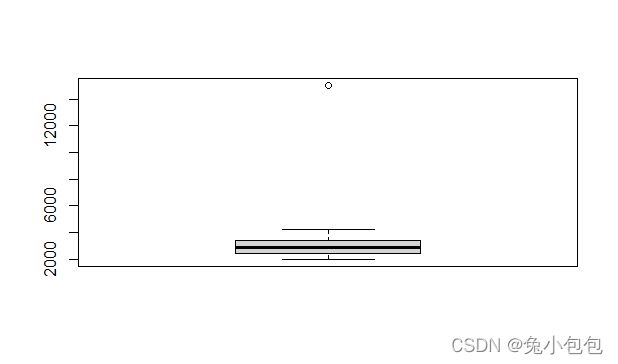
boxplot(salarym)
boxplot.stats(salarym)
$stats
[1] 2000 2400 2875 3400 4200

$n
[1] 20

$conf
[1] 2521.701 3228.299

$out
[1] 15000

(2).Grubbs 检验
Grubbs 检验是由Grubbs F.E.提出来的用来探索来自于正态总体的单变量数据的离群值。Grubbs 检验是基于正态总体的假设，也就说在做检验前需要先检验数据的正态性。Grubbs 检验每次只能检验一个离群值。
Grubbs 检验的假设：
H0：数据集中没有离群值
H1：数据集中至少有一个离群值
R中的outliers包是专门用来做离群值检测的包，其中grubbs.test（）函数可以进行Grubbs 检验,其用法grubbs.test(x, type = 10, opposite = FALSE, two.sided = FALSE)
x是待检验数据，type表示检验类型，10表示检验一个离群值（默认值）,11表示检验两个尾部上的两个离群值，20表示在一个尾部检验两个离群值。Opposite表示检验反方向上的离群值。Two.sided表示是否进行双边检验。

(3).Dixon’s Q 检验
R中outliers包里的dixon.test（）函数可以用做Dixon’s Q 检验。其用法是dixon.test(x, type = 0, opposite = FALSE, two.sided = TRUE)
x是待检验数据，type表示检验类型,根据样本量大小选择不同的类型，具体的选择有：10(样本量 3-7），11（样本量8-10），21（样本量11-13），22（14及以上）。opposite表示检验反方向上的离群值。two.sided表示是否进行双边检验。

6.3双变量数据分析

分类数据对分类数据

(1). 二维表
R的table()函数可以把双变量分类数据整理成二维表形式，table命令处理双变量数据类似于处理单变量数据，只是参数(变量)由原来的一个变成了两个。

smoke=c(“Y”,“N”,“N”,“Y”,“N”,“Y”,“Y”,“Y”,“N”,“Y”)
study=c("<5h",“5-10h”,“5-10h”,">10h",">10h","<5h",“5-10h”,"<5h", “>10h”,“5-10h”)
table(smoke,study)
study
smoke <5h >10h 5-10h
N 0 2 2
Y 3 1 2

对于二维表，我们经常要计算某个数据占行、列汇总数的比例或是占总的比例，也就是边缘概率。R可以很简单地计算这些比例，用函数prop.table( )，其句法是：prop.table(x, margin)，当margin=1时，表示各个数据占行汇总数的比例，margin=2表示各个数据占列汇总数的比例，省略时，表示占总和的比例。

tab=table(smoke,study)
prop.table(tab,1)
study
smoke <5h >10h 5-10h
N 0.0000000 0.5000000 0.5000000
Y 0.5000000 0.1666667 0.3333333

(2). 复杂（复式）条图
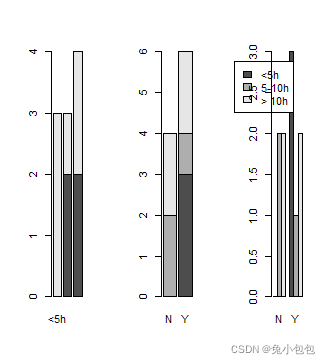
条图用等宽直条的长短来表示相互独立的各指标数值大小，该指标可以是连续性变量的某汇总指标，也可以是分类变量的频数或构成比。各（组）直条间的间距（距离）应相等，其宽度一般与直条的宽度相等或为直条宽度的一半。R作条形图的函数是barplot( )，不过在作条形图前需对数据进行分组。

par(mfrow=c(1,3)) #设置图形窗口以一行三列形式输出
barplot(table(smoke,study)) #以study为分类变量作条形图
barplot(table(study,smoke)) #以smoke为分类变量作条形图
barplot(table(study,smoke),beside=T,legend.text=c("<5h",“5-10h”, “> 10h”)) # 设置图例

其中main参数用来为图像添加标题，此外，还可以用sub添加副标题。beside参数设置为False时，作出的图是分段式条形图，True时作出的条形图是并列式，R默认的是False。参数legend.text为图添加图例说明。

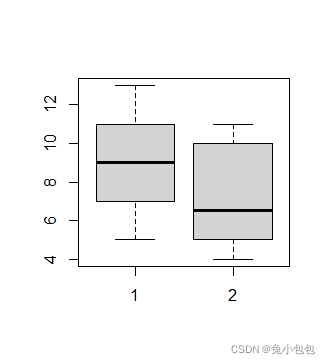
分类数据对数据

x=c(5,5,13,7,11,11,9,8,9)
y=c(11,8,4,5,9,5,10,5,4,10)
boxplot(x,y)

数值型数据对数值型数据

比较两个数值变量的方法很多，可以从不同角度去比较。比如对两个独立的数值变量，可以比较它们的分布是否相同，也可以分析是否存在着某种相关关系、回归关系等。
(1). 散点图
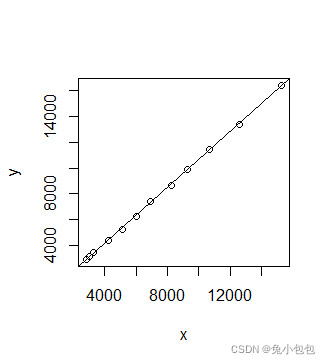
简单分析两个数值变量的关系，经常使用散点图，在R里画散点图非常简单，只要用plot( )函数就可以了。

data.entry(c(NA)) #用数据编辑器编辑数据
plot(x,y) #做散点图
abline(lm(y~x)) #添加趋势线)

(2). 相关系数
相关系数用来反映两个数值变量的相关程度。经济变量之间的关系，大体可分为两类：
（1）确定性关系：研究的是确定现象非随机变量间的关系。
（2）统计相关关系：研究的是非确定现象随机变量间的关系。
注意：
①不线性相关并不意味着不相关；
②有相关关系并不意味着一定有因果关系；
③相关分析研究一个变量对另一个（些）变量的统计依赖关系，但它们并不意味着一定有因果关系。
④相关分析对称地对待任何（两个）变量，两个变量都被看作是随机的。

Person相关系数的取值范围是[-1,1]，当-1 < r < 0，表示具有负线性相关，越接近-1，负相关性越强。0 < r < 1，表示具有正线性相关，越接近1，正相关性越强。r = -1表示具有完全负线性相关，r = 1表示具有完全正线性相关 r = 0表示两个变量不具有线性相关性。

cor(x,y)
[1] 0.9997906
cor(y,x)
[1] 0.9997906
cor(x,y,method = “spearman”)
[1] 1

6.4多变量数据分析

访问数据框数据

在统计分析中经常碰到多变量数据，对于多变量数据，经常以类似电子表格的形式储存，以列表示变量，行表示观察值或样品。R使用数据框（data frame）形式储存多变量数据，关于数据框我们在第2.6.6节里已介绍了一些基础知识。在这里我们再深入地介绍一下如何访问数据框数据以及数据框拆分等问题。
(1). 数据框绑定“attach”
在前面我们已经接触过了attach( )和detach( )函数，但没有详细介绍它们的作用，其实这两个函数是应用数据框时很有用的工具。attach( )函数将数据框“连接（绑定）”入当前的名字空间，从而可以直接用数据框中的变量名访问而不必用“数据框名$变量名”这种格式。当变量较多时，通常将其存为一个文本文件。

yx=read.table(“reg1.txt”,header=T)
yx
t y x
1 1990 2937 2822
2 1991 3149 2990
…
11 2000 13395 12582
12 2001 16386 15301

该数据框有三个变量，对于数据框的变量我们不能直接引用，要用“数据框名$变量名”的格式，或是利用attach( )把数据框“连接（绑定）”入当前的名字空间。

x
错误：找不到这个目标对象"x"
yx$x
[1] 2822 2990 3297 4255 5127 6038 6910 8234 9263 10683 12582 15301
attach(yx)
x
[1] 2822 2990 3297 4255 5127 6038 6910 8234 9263 10683 12582 15301
detach() ##要取消连接，用函数detach（）即可。
x
错误：找不到这个目标对象"x"

R语言的名字空间管理是比较独特的。它在运行时保持一个变量搜索路径表，在读取某个变量时到这个变量搜索路径表中由前向后查找，找到最前一个。在赋值时总是在位置1赋值（除非有另外的特别指定）。读取某个变量的默认位置是在变量搜索路径表的位置2，rm( )默认去掉位置2上的数据，并（而）不删除原始数据。

x=“That’s wrong”
x
[1] “That’s wrong”
rm(x)
x #注意这里显示的是上个例子中yx数据集里的x变量
[1] 2822 2990 3297 4255 5127 6038 6910 8234 9263 10683 12582 15301
detach()
x
错误：找不到这个目标对象"x"

(2). 以数组形式访问
   其实，数据框可看作是特殊的数组，因此我们可以以数组形式访问数据框。数组是储存数据的一种有效方法，可以按行或列访问，就像电子表格一样，但输入的数据必须是同一类型。数据框之所以可以看作数组是因为数据框的列表示变量、行表示样本观察数，因此我们可以访问指定的行或列，在2.6.6我们介绍了可以利用“数组名[行，列]”的形式访问。
   > yx[,"y"]         #返回y变量的所有样本观察数

[1] 2937 3149 3483 4349 5218 6242 7408 8651 9876 11444 13395 16386

yx[,1] #返回第一列变量的所有样本观察数
[1] 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
yx[1:5,1:3] #返回第1至第5行，第1至第3列的观察数
t y x
1 1990 2937 2822
2 1991 3149 2990
3 1992 3483 3297
4 1993 4349 4255
5 1994 5218 5127
yx[1,]
t y x
1 1990 2937 2822
yx[1,2] #返回第2变量的第1个样本观察数
[1] 2937
yx[,] #返回所有行所有列数据

(3). 以列表形式访问数据框
列表是比数据框更为一般、更为广泛。列表是对象的集合，而且这些对象可以是不同类型的。数据框是特殊的列表，数据框的列看作向量，而且要求是同一类型对象。可以以列表形式访问数据框，只要在列表名称后面加$符号，再写上变量名就可以了。如：

yxKaTeX parse error: Expected 'EOF', got '#' at position 11: x #̲返回x变量的所有样本观察数 […形式访问外，还可以用列表名[[变量名(号)]]形式访问：
yx[[‘y’]] #返回y变量的所有样本观察数
[1] 2937 3149 3483 4349 5218 6242 7408 8651 9876 11444 13395 16386
yx[[1]] #返回t变量的所有样本观察数
[1] 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001

列表还可以筛选出符合我们条件的数据，比如对上面的数据要得到1998后的资料，可以按如下的方法得到（去做）。

yx[yx$t>‘1998’,]
t y x
9 1998 9876 9263
10 1999 11444 10683
11 2000 13395 12582
12 2001 16386 15301

多变量的数据分析

(1). 多维列联表
前面介绍了用table( )函数生成一、二维表，其实table( )函数还可以生成多维表，假如存在x、y、z三个变量，table(x,y)则生成x、y二维表，table(x,y,z)生成每个z值关于x、y的二维表（由于计算机作三维及三维以上的表格不方便，所以就用这种方式显示，类似于多维数组显示方式）。

library(MASS)
data(Cars93)
attach(Cars93)
names(Cars93)
[1] “Manufacturer” “Model”
[3] “Type” “Min.Price”
[5] “Price” “Max.Price”
[7] “MPG.city” “MPG.highway”
[9] “AirBags” “DriveTrain”
[11] “Cylinders” “EngineSize”
[13] “Horsepower” “RPM”
[15] “Rev.per.mile” “Man.trans.avail”
[17] “Fuel.tank.capacity” “Passengers”
[19] “Length” “Wheelbase”
[21] “Width” “Turn.circle”
[23] “Rear.seat.room” “Luggage.room”
[25] “Weight” “Origin”
[27] “Make”
price=cut(Price,c(0,12,20,max(Price))) #把Price按区间分成三组levels(price)=c(“cheap”,“okay”,“expensive”) ＃对price的因子命名
mpg=cut(MPG.highway,c(0,20,30,max(MPG.highway)))
levels(mpg)=c(“gas guzzler”,“oky”,“miser”)
table(Type)
Type
Compact Large Midsize Small Sporty Van
16 11 22 21 14 9
table(price,Type)
Type
price Compact Large Midsize Small Sporty Van
(0,12] 3 0 0 18 1 0
(12,20] 9 3 8 3 9 8
(20,61.9] 4 8 14 0 4 1
table(price,Type,mpg)
, , mpg = gas guzzler

       Type

price Compact Large Midsize Small Sporty Van
(0,12] 0 0 0 0 0 0
(12,20] 0 0 0 0 0 2
(20,61.9] 0 0 0 0 0 0

, , mpg = oky

       Type

price Compact Large Midsize Small Sporty Van
(0,12] 1 0 0 4 0 0
(12,20] 5 3 6 0 6 6
(20,61.9] 4 8 14 0 4 1

, , mpg = miser

       Type

price Compact Large Midsize Small Sporty Van
(0,12] 2 0 0 14 1 0
(12,20] 4 0 2 3 3 0
(20,61.9] 0 0 0 0 0 0

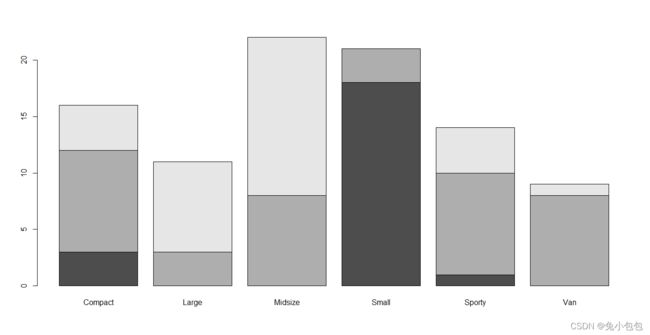
(2). 复式条形图
多变量数据统计分析中经常用到复式条形图，复式条形图是指两条或两个以上小直条组成的条形图。与简单条形图相比，复式条形图多考察了一个分组因素，常用于考察比较两组研究对象的某观察指标。作复式条形图之前应先对数值数据进行分组，然后用table( )函数作频数表。作复式条形图的函数是barplot( )，R默认的分段式复式条形图，要作并列式复式条形图，要设置参数beside＝TRUE。

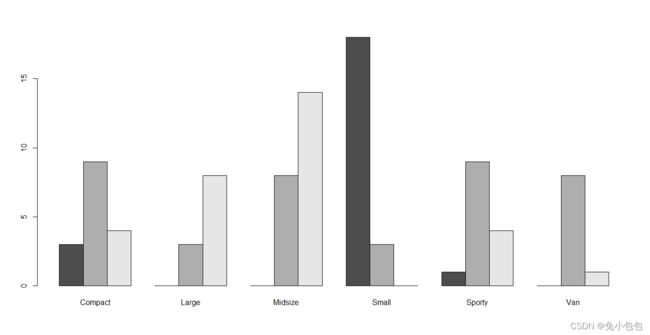
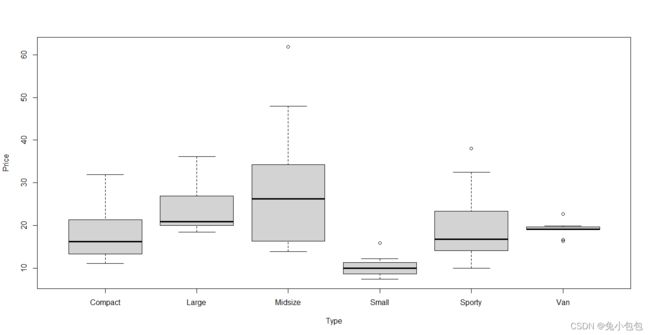
(3). 并列箱线图
对于多变量数据经常要用到箱线图来分析各个变量的分布情况。R作箱线图的函数是boxplot( )，其用法前面已经介绍过了，这里主要通过几个例子来分析一下如何作多变量的箱线图。

(4). 点带图（stripchart）
箱线图经常用来比较各变量的分布情况，尤其是当每个变量都有很（较）多的观察值时，点带图也可以用来比较各变量的分布情况，但主要用在样本观察值比较少时。R作点带图的函数是stripchart( )，对于双变量数据其用法是stripchart（z～t），z变量在t变量上的分布情况，不同的是这里z变量刻度在x轴上，而t变量在y轴上。
stripchart(Type~price)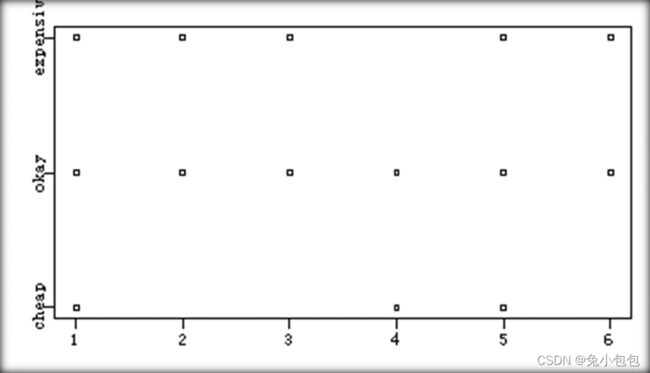
（1）重叠散点图
有时出于研究的需要，需将两个或多组两个变量的散点图绘制在同一个图中，这样可以更好比较它们之间的相关关系，这时就可以绘重叠散点图。

plot(iris[,1],iris[,3],type=“n”) # 绘制iris第1和第3列的散点图，不显示点type=“n”
text(iris[,1],iris[,3],cex=0.6) # 显示样本序号，缩小字体cex=0.6

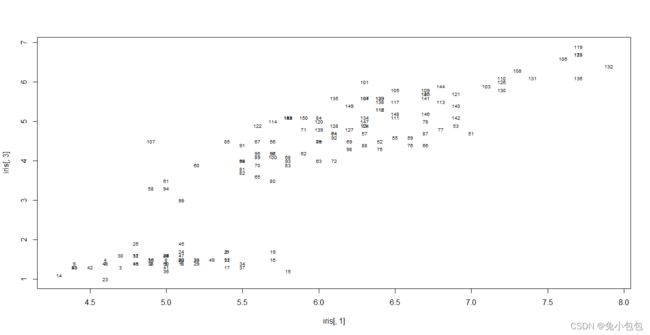
（2）矩阵式散点图
当欲同时考察三个或三个以上的数值变量间的相关关系时一一绘制它们之间的简单散点图，十分麻烦。利用矩阵式散点图比较合适，这样可以快速发现多个变量间主要相关性，这一点在多元线性回归显得尤为重要。R作矩阵式散点图的函数是pairs（）。
> pairs(iris)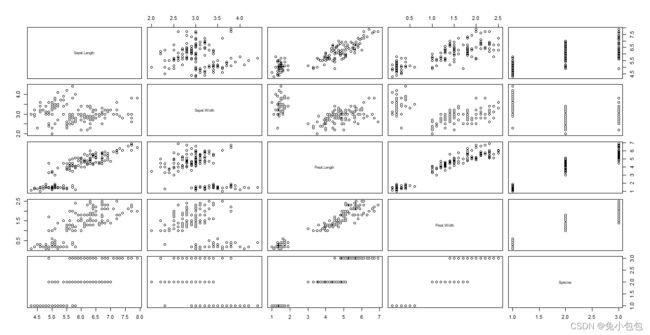

第七章参数假设检验

假设检验的基本思想

在数学推导上，参数假设检验是与区间估计是相联系的，而在方法上，二者又有区别。对于区间估计，人们主要是通过数据推断未知参数的取值范围；而对于假设检验，人们则是做出一个关于未知参数的假设，然后根据观察到的样本判别该假设是否正确。在R中，区间估计和假设检验使用的是同一个函数。

u.test<-function(a,mu,thegma)

• { Se=thegma/sqrt(length(a))
• u=(mean(a)-mu)/Se
• p=2*(1-pnorm(abs(u)))
• return(list(u=u, p=p))
• }

a<-c(4.89,5.99,5.89,6.22,4.79,5.47,4.50,6.61,4.25,6.67,4.46,4.50,6.97,5.39,

•  4.56,5.03,2.54,5.27,4.48,4.05)
  

u.test(a,5,1)
$u
[1] 0.5657252

$p
[1] 0.5715806

正态总体单样本参数假设检验

均值的检验

1方差已知情形

u.test<-function(a,mu,thegma,alternative=“twoside”)

• { Se=thegma/sqrt(length(a))
• u=(mean(a)-mu)/Se
• if (alternative==“twoside”) p=2*(1-pnorm(abs(u)))
• else if (alternative==“less”) p=pnorm(u)
• else p=1-pnorm(u)
• return(list(u=u, p=p))
• }

b=c(22,24,21,24,23,24,23,22,21,25)
u.test(b,25,2.4,alternative=“less”) #左侧检验
$u
[1] -2.766993

$p
[1] 0.002828799

2方差未知情形

x=c(50.2,49.6,51.0,50.8,50.6,49.8,51.2,49.7,51.5,50.3,51.0,50.6)
t.test(x,mu=50,alternative =“greater”)

One Sample t-test

data: x
t = 2.9564, df = 11, p-value = 0.006529
alternative hypothesis: true mean is greater than 50
95 percent confidence interval:
50.20609 Inf
sample estimates:
mean of x
50.525

方差检验

x=c(512.952899108198, 503.85274864927, 495.06951127009, 477.193305294993,

• 509.400520346022, 493.249014260413, 492.456674317536, 530.078195416527, 
  

• 498.757258963417, 522.657000900506, 510.041124496973, 490.505063978937, 
  

• 536.24855605503, 530.039965979141, 495.559165160148, 466.840695851664, 
  

• 510.702680801237, 524.485012890925, 490.37616974915, 485.579333872921
  

• )

var.test1<-function(x, sigma2){

• n<-length(x)
• S2=var(x)
• df=n-1
• chi2<-df*S2/sigma2;
• P<-pchisq(chi2,df)
• data.frame(var=S2, df=df, chisq2=chi2, P_value=P)
• }

var.test1(x,400)
var df chisq2 P_value
1 346.8209 19 16.47399 0.3745438

7.3正态总体双样本参数假设检验

双样本方差的检验（方差齐性检验）

x1=c(24, 29, 39, 40, 32, 32, 31, 44, 37, 37, 50, 28, 24, 48, 25, 40, 32, 34, 35, 41)
x2=c(44, 34, 36, 38, 30, 30, 35, 38, 40, 46, 38, 35, 38, 36, 38, 40, 34, 37, 40, 46)
var.test(x1,x2)

F test to compare two variances

data: x1 and x2
F = 2.9283, num df = 19, denom df = 19, p-value =
0.02385
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
1.159058 7.398216
sample estimates:
ratio of variances
2.928304

两样本均值检验

1两独立样本t检验
Step1在作两样本均值检验时，需要验证样本是否服从正态分布，即正态性检验。
Step2判断两个样本是否有相同的方差，可以根据方差齐次检验判别。
Step 3 t检验判断均值。对于R软件中，两个独立样本检验两种情况都用一个函数，t.test。
用法如下： t.test（x1,x2,var.equal=T） #方差齐次条件满足时。
t.test（x1,x2） #默认方差非齐次时。

x1=c(48,47,44,45,46,47,43,47,42,48)
x2=c(36,45,47,38,39,42,36,42,46,35)
var.test(x1,x2)

F test to compare two variances

data: x1 and x2
F = 0.22732, num df = 9, denom df = 9, p-value =
0.03793
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.05646413 0.91520616
sample estimates:
ratio of variances
0.2273243

t.test(x1,x2)

Welch Two Sample t-test

data: x1 and x2
t = 3.2882, df = 12.891, p-value = 0.005939
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1.746412 8.453588
sample estimates:
mean of x mean of y
45.7 40.6

2两配对样本t检验

before = c(94.5,101,110,103.5,97,88.5,96.5,101,104,116.5)
after = c(85,89.5,101.5,96,86,80.5,87,93.5,93,102)
t.test(before,after,paired=T)

Paired t-test

data: before and after
t = 14.164, df = 9, p-value = 1.854e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
8.276847 11.423153
sample estimates:
mean of the differences
9.85

7.4比例假设

单样本比例检验

proptest<-function(x,n,p,alternative)

• { Se=sqrt(p*(1-p)/n)
• u=(x/n-p)/Se
• if (alternative==“twoside”) p=2*(1-pnorm(abs(u)))
• else if (alternative==“less”) p=pnorm(u)
• else p=1-pnorm(u)
• return(list(u=u, p=p))
• }

proptest(45,100,0.5,alternative=“twoside”)
$u
[1] -1

$p
[1] 0.3173105

proptest(450,1000,0.5,alternative=“twoside”)
$u
[1] -3.162278

$p
[1] 0.001565402

两样本比例检验

prop.test(c(45,56),c(45+35,56+47))

2-sample test for equality of proportions with
continuity correction

data: c(45, 56) out of c(45 + 35, 56 + 47)
X-squared = 0.010813, df = 1, p-value = 0.9172
alternative hypothesis: two.sided
95 percent confidence interval:
-0.1374478 0.1750692
sample estimates:
prop 1 prop 2
0.5625000 0.5436893

第八章非参数检验

8.1图示法

1直方图
2茎叶图
3Q-Q图
仅用于验证正态性
以标准正态分布的分位数为横坐标，以处在相同百分位的样本分位数为纵坐标，把样本表现在直角坐标系中的散点。如果资料服从正态分布，则样本点应该呈一条围绕第一象限对角线的直线。也可以用累计概率来作图，成为P-P，但相较之下以Q-Q图为佳，效率较高。
4经验分布图
5箱式图

8.2卡方检验

卡方分布

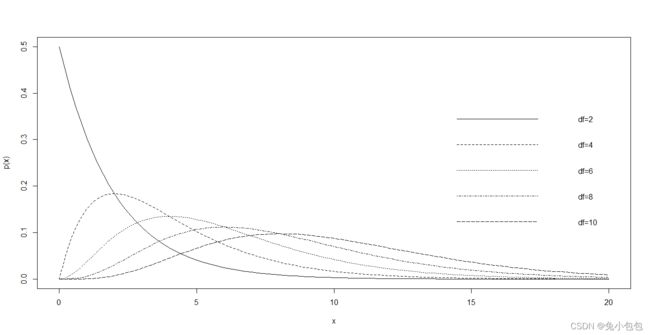
x=seq(0,20,0.1) #生成x序列
curve(dchisq(x,2),0,20,ylab=“p(x)”)
curve(dchisq(x,4),add=T,lty=2)
curve(dchisq(x,6),add=T,lty=3)
curve(dchisq(x,8),add=T,lty=4)
curve(dchisq(x,10),add=T,lty=5)
legend(13,0.4,c(“df=2”,“df=4”,“df=6”,“df=8”,“df=10”), lty=1:5, bty=“n”)

卡方拟合优度检验

卡方拟合优度检验(Chi-squared goodness of fit tests)用来检验样本是否来自于特定类型分布的一种假设检验。

1离散型分布验证

freq = c(22,21,22,27,22,36)
probs = c(1,1,1,1,1,1)/6 # 指定理论概率(多项分布)
chisq.test(freq,p=probs)

Chi-squared test for given probabilities

data: freq
X-squared = 6.72, df = 5, p-value = 0.2423

freq = c(100,110,80,55,14)
probs = c(29,21,17,17,16)/100
chisq.test(freq,p=probs)

Chi-squared test for given probabilities

data: freq
X-squared = 55.395, df = 4, p-value = 2.685e-11

2连续型分布验证

x<-c(159.8,178.5,168.9,183.2,174.0,160.9,180.0,171.7,152.4,174.3,170.2,185.3,169.6,160.1,158.9,164.6, 172.2, 168.0, 182.1, 171.1)
fn=table(cut(x,breaks=c(min(x),160,170,180,190,max(x))))
F=pnorm(c(min(x),160,170,180,190,max(x)),170,8)
P=c(F[1],F[2]-F[1],F[3]-F[2],F[4]-F[3],1-F[4])
chisq.test(fn,p=P)

Chi-squared test for given probabilities

data: fn
X-squared = 26.537, df = 4, p-value = 2.466e-05

卡方独立性检验

卡方独立性检验(Chi-squared tests of independence)，在原假设两个因素相互独立的前提下，比较两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。基于这一原理，构造同前章节中的卡方统计量来检验列联表中的两个因子是否相互独立。

yesbelt = c(12813,647,359,42)
nobelt = c(65963,4000,2642,303)
chisq.test(rbind(yesbelt,nobelt))

Pearson's Chi-squared test

data: rbind(yesbelt, nobelt)
X-squared = 59.224, df = 3, p-value = 8.61e-13

卡方两样本同质检验

卡方同质性检验(Chi-squared tests for homogeneity)，检验各行是否来自同一个总体。直观地，如果各行因子来自于相同的总体，每一类的出现概率应该是差不多的，而卡方统计量则将再次帮助我们解释“差不多” 的含义。

die.fair = sample(1:6,100,p=c(1,1,1,1,1,1)/6,rep=T) # 均匀骰子
die.bias = sample(1:6,100,p=c(.5,.5,1,1,1,2)/6,rep=T) # 不均匀骰子
res.fair = table(die.fair);res.bias = table(die.bias)
count=rbind(res.fair,res.bias)
count
1 2 3 4 5 6
res.fair 15 15 16 17 12 25
res.bias 12 8 18 16 10 36
chisq.test(count)

Pearson's Chi-squared test

data: count
X-squared = 4.7771, df = 5, p-value = 0.4437

chisq.test(count)$exp # 获得期望频数
1 2 3 4 5 6
res.fair 13.5 11.5 17 16.5 11 30.5
res.bias 13.5 11.5 17 16.5 11 30.5

8.3秩和检验

秩的概念

x = c(21240,4632, 22836,5484,5052,5064,6972,7596,14760,15012, 18720, 9480, 4728, 67200,52788)
(Ri = rank(x))
[1] 12 1 13 5 3 4 6 7 9 10 11 8 2 15 14

单样本符号秩检验

x = c(21240,4632, 22836,5484,5052,5064,6972,7596,14760,15012, 18720, 9480, 4728, 67200,52788)
stem(x)

The decimal point is 4 digit(s) to the right of the |

0 | 55555789559
2 | 13
4 | 3
6 | 7

wilcox.test (x, mu=5080)

Wilcoxon signed rank exact test

data: x
V = 109, p-value = 0.003357
alternative hypothesis: true location is not equal to 5080

两独立秩和检验

两样本wilcoxon秩和检验也可由函数wilcox.test完成，其本质是一种非参数的检验方法，用法和单样本检验相似。
假定第一个样本有m个观测值，第二个有n个观测值。把两个样本混合之后把这m+n个观测值按升幂排序，记下每个观测值在混合排序下面的秩。再分别把两个样本所得到的秩相加。记第一个样本观测值的秩的和为W1，而第二个样本秩的和为W2。这两个值可以互相推算，称为Wilcoxon统计量。
该统计量的分布和两个总体分布无关。由此分布可以得到p值。直观上看，如果W1与W2之中有一个显著地大，则可以选择拒绝原假设。该检验需要的唯一假定就是两个总体的分布有类似的形状，但不一定要求分布是对称的。

多个独立样本秩和检验

Kruskal-Wallis检验为非参数检验，可在数据非正态的情况下代替单因素方差分析。它的使用方式和用Wilcoxen符号秩检验代替t检验是一样的。另外它也是一个基于原始数据秩的检验，故不要求数据的正态性。
当你不肯定单因素检验中的正态性假定是否成立时，便可考虑Kruskal-Wallis检验。

kruskal.test(weight ~ group,data=PlantGrowth)

Kruskal-Wallis rank sum test

data: weight by group
Kruskal-Wallis chi-squared = 7.9882, df = 2,
p-value = 0.01842

scores = c(4,3,4,5,2,3,4,5,4,4,5,4,4,4,5,5,4,5,4,4,5,5,4,5,3,4,2,4,4,5,3,4,2,2,1,1)
person = c(1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,2)
boxplot(scores~person) #做一个箱线图比较分布
kruskal.test(scores ~ person)

Kruskal-Wallis rank sum test

data: scores by person
Kruskal-Wallis chi-squared = 6.9383, df = 2,
p-value = 0.03114

多个相关样本的秩和检验

X=matrix(c(20.3,21.2,18.2,18.6,18.5,25.6,24.7,19.3,19.3,20.7, 24.0, 23.1,20.6,19.8,21.4),5)
friedman.test(X)

Friedman rank sum test

data: X
Friedman chi-squared = 7.6, df = 2, p-value =
0.02237

8.4 K-S检验

K-S单样本总体分布验证

检验是否服从已知参数的连续型分布

x=rnorm(50)
y=runif(50,0,1)
ks.test(x, “pnorm”, mean=0, sd=1)

One-sample Kolmogorov-Smirnov test

data: x
D = 0.13431, p-value = 0.3003
alternative hypothesis: two-sided

ks.test(y, “punif”, 0,1 )

One-sample Kolmogorov-Smirnov test

data: y
D = 0.15158, p-value = 0.1812
alternative hypothesis: two-sided

ks.test(x,“pexp”,0.5)

One-sample Kolmogorov-Smirnov test

data: x
D = 0.44256, p-value = 1.934e-09
alternative hypothesis: two-sided

K-S两独立样本同质检验

x1=c(48,47,44,45,46,47,43,47,42,48)
x2=c(36,45,47,38,39,42,36,42,46,35)
boxplot(x1,x2,horizontal=T,names=c(“x1”,“x2”))
ks.test(x1,x2)

Two-sample Kolmogorov-Smirnov test

data: x1 and x2
D = 0.6, p-value = 0.05465
alternative hypothesis: two-sided

8.5常用正态性检验

偏度、峰度检验法

1用样本偏度、峰度的极限分布做检验
偏度(Skewness)反映单峰分布的对称性。峰度(Kurtosis)反映分布峰的尖峭程度。


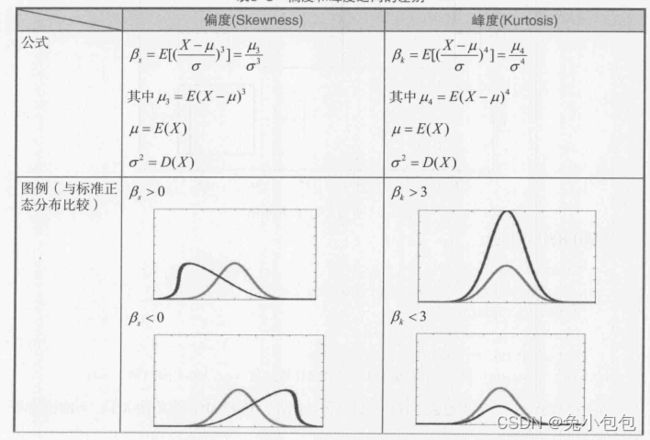
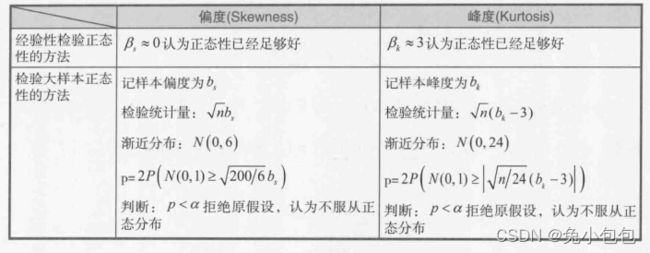
2Jarque-Bera检验（偏度和峰度的联合分布检验法）

Shapiro-Wilk（W检验）

1一元正态性检验
夏皮洛—威尔克(Shapiro-Wilk)检验也称为W检验，这个检验当8≤n≤50时可以使用。过小样本n<8对偏离正态分布的检验不太有效。大样本可以使用后面介绍的K-S检验。
2多元正态分布检验

其他常用正态检验

1AD正态性检验
2Cramer-von Mises正态性检验
3Lilliefors正态性检验
4Pearson卡方正态性检验
5Shapiro-Francia正态性检验

第九章方差分析

t检验用于检验两个独立正态总体均值是否相等，当要同时检验多个总体的均值是否存在差异，就不能用t检验，需用利用方差分析（Analysis of Variance，简称ANOVA），其本质也是一种均值假设检验，通过对方差来源进行分解，判别某一个或多个因素下各个水平的因变量均值是否有明显的差异，从而判别哪些因素对因变量有显著影响。

9.1单因素方差分析

方差分析是对全部样本观察值的差异（用样本方差来衡量）进行分解，将某种因素下各样本观察值之间可能存在的系统性误差与随机误差加以比较，据以推断各总体之间是否存在显著性差异。单因素方差分析就是只考虑一个因素对结果的影响。

在R语言中做单因素方差分析（one-way analysis of variance）的函数为oneway.test。它要求有一变量观测值（本例为income），而另一个因子来描述分类情况（本例为group）

sta<-c(3306,6496,3996,5572,4887,5084,6168,4740,4250,4031,

•    3955,5291,4995,4398,4392,3475,4643,5562,3159,4403)
  

Fina<- c(3882,4663,2429,5399,5127,3896,4039,4576,4012,3214,

•      4525,4938,3716,4248,5318,2891,2737,3395,4053,6495)
  

Trade<-c(4502,3222,3651,3189,4246,5004,4652,6058,2889,3567,

•      2409,3710,4681,4485,3441,3356,3922,4455,2790, 4023)
  

income<-c(sta,Fina,Trade)
group<-c(rep(1,20),rep(2,20),rep(3,20))
oneway.test(income ~ group, var.equal=T)

One-way analysis of means

data: income and group
F = 3.1857, num df = 2, denom df = 57, p-value =
0.0488

data(PlantGrowth)
oneway.test(weight ~ group, data=PlantGrowth, var.equal=T)

One-way analysis of means

data: weight and group
F = 4.8461, num df = 2, denom df = 27, p-value =
0.01591

更多有关分析的详细信息可通过函数anova和aov按下面的方式得到。应用函数anova需要在线性模拟函数lm产生的结果基础上调用它。

anova(lm(weight ~ group, data=PlantGrowth))
Analysis of Variance Table

Response: weight
Df Sum Sq Mean Sq F value Pr(>F)
group 2 3.7663 1.8832 4.8461 0.01591 *
Residuals 27 10.4921 0.3886
Signif. codes:
0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

summary(aov(weight ~ group, data=PlantGrowth))
Df Sum Sq Mean Sq F value Pr(>F)
group 2 3.766 1.8832 4.846 0.0159 *
Residuals 27 10.492 0.3886

---

Signif. codes:
0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

9.2两因素方差分析

不考虑交互作用的两因素方差分析

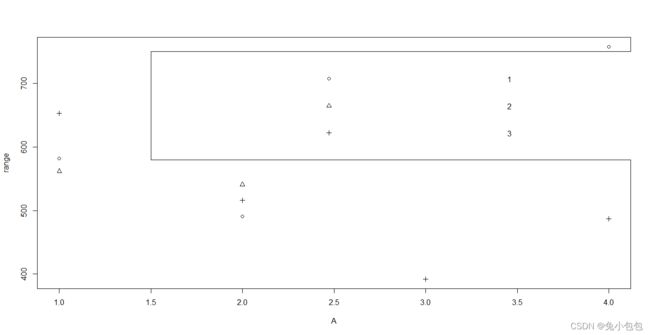
range=c(582,562,653,491,541,516,601,709,392,758,582,487)
A=c(1,1,1,2,2,2,3,3,3,4,4,4)
B=c(1,2,3,1,2,3,1,2,3,1,2,3)
plot(range~A,pch=B) # pch 不同符号表示
legend(1.5,750,legend=1:3,pch=B) #（1.5,750）处添加图例
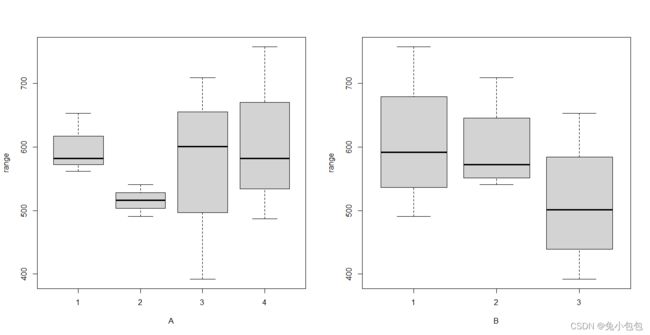
par(mfrow=c(1,2))
boxplot(range~A,xlab=“A”); boxplot(range~B,xlab=“B”)
par(mfrow=c(1,1))
A = factor(A) ; B = factor(B) # 首先将A、B声明（转换）成因子
(range.aov <- aov(range ~ A + B )) # 拟合方差分析模型
Call:
aov(formula = range ~ A + B)

Terms:
A B Residuals
Sum of Squares 15759.00 22384.67 73198.00
Deg. of Freedom 3 2 6

Residual standard error: 110.4521
Estimated effects may be unbalanced

summary(range.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 3 15759 5253 0.431 0.739
B 2 22385 11192 0.917 0.449
Residuals 6 73198 12200

A=c(1,2,3,4,1,2,3,4,1,2,3,4)
B=c(1,1,1,1,2,2,2,2,3,3,3,3)
A = factor(A) ; B = factor(B)
aov(beef ~ A + B )
Call:
aov(formula = beef ~ A + B)

Terms:
A B Residuals
Sum of Squares 588.2500 112.1667 1412.5000
Deg. of Freedom 3 2 6

Residual standard error: 15.34329
Estimated effects may be unbalanced

beef.aov <- aov(beef ~ A + B )
summary(beef.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 3 588.3 196.08 0.833 0.523
B 2 112.2 56.08 0.238 0.795
Residuals 6 1412.5 235.42

考虑交互作用的两因素方差分析

单因素ANOVA是用于处理（总体）平均值相等的假设检验，无重复双因素ANOVA用分块来说明无总体变化，也是一种总体平均值相等的假设检验。这一节讲述有重复双因素ANOVA，它可用于检验两总体的效果。该检验适用于析因实验。这里限制为完全的随机化设计中的双因子。
如果A、B两因素存在交互影响，这种交互作用也可能对各观察值组水平的差异产生影响，这就需要对每种水平的组合进行若干次独立观察。故这种方差分析也称为重复观察的两因素方差分析 >Y=c(60.7,61.1,61.5,61.3,61.6,62.0,61.7,61.1,61.5,60.8,61.7,61.2,62.2,62.8,62.1,61.7,60.6,60.3,60.6,61.0,61.4,61.5,60.7,60.9)

A=c(rep(1,8),rep(2,8),rep(3,8))
B=c(1,1,2,2,3,3,4,4, 1,1,2,2,3,3,4,4, 1,1,2,2,3,3,4,4)
A=factor(A); B=factor(B)
rate.aov <- aov(Y ~ A+B+A*B)
rate.aov
Call:
aov(formula = Y ~ A + B + A * B)

Terms:
A B A:B Residuals
Sum of Squares 3.083333 3.630000 0.300000 1.140000
Deg. of Freedom 2 3 6 12

Residual standard error: 0.3082207
Estimated effects may be unbalanced

summary(rate.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 2 3.083 1.542 16.228 0.000387 ***
B 3 3.630 1.210 12.737 0.000487 ***
A:B 6 0.300 0.050 0.526 0.778290
Residuals 12 1.140 0.095

---

Signif. codes:
0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Y=c(2.8,2.73,2.04,1.33,1.58,1.23,

•     + 3.29,2.68,1.5,1.4,1,1.82,
  

•     + 2.54,2.59,3.15,2.88,1.92,1.33)
  

A=c(rep(1,6),rep(2,6),rep(3,6))
B=c(1,1,2,2,3,3, 1,1,2,2,3,3, 1,1,2,2,3,3)
A=factor(A); B=factor(B)
aov(Y ~ A + B + A*B)
Call:
aov(formula = Y ~ A + B + A * B)

Terms:
A B A:B Residuals
Sum of Squares 0.816044 5.028211 2.272489 1.054750
Deg. of Freedom 2 2 4 9

Residual standard error: 0.3423367
Estimated effects may be unbalanced

ad.aov <- aov(Y ~ A + B + A*B)
summary(ad.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 2 0.816 0.4080 3.482 0.075867 .
B 2 5.028 2.5141 21.452 0.000376 ***
A:B 4 2.272 0.5681 4.848 0.023161 *
Residuals 9 1.055 0.1172

---

Signif. codes:
0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

第十章线性回归模型

回归分析是对客观事物数量依存关系的分析，是统计中的一个常用的方法，被广泛的应用于社会经济现象变量之间的影响因素和关联的研究。根据自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

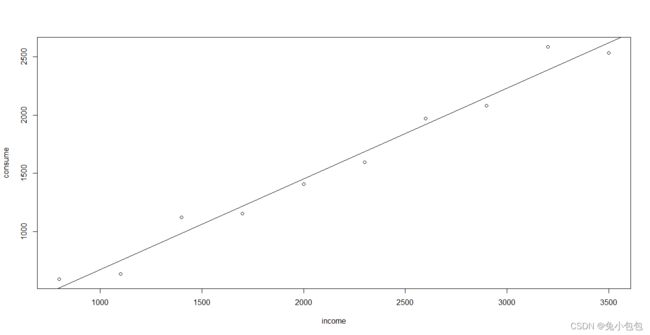
consume=c(594,638,1122,1155,1408,1595,1969,2078,2585,2530)
income=c(800,1100,1400,1700,2000,2300,2600,2900,3200,3500)
cor(income,consume)
[1] 0.9882517
plot(income,consume)
abline(lm(consume~income))

10.2一元线性回归

一元线性回归概述

回归分析(regression analysis)是研究一个变量关于另一个（些）变量的具体依赖关系的计算方法和理论。
通常前一个变量被称为被解释变量（Explained Variable）或因变量（Dependent Variable）或响应变量（Response），后一个（些）变量被称为解释变量（Explanatory Variable）或自变量（Independent Variable）或者协变量（Covariate）。因变量往往又更加形象地称之为输出变量（Output variable），自变量称为输入变量（Input variable）。
由于变量间关系的随机性，回归分析关心的是根据解释变量的已知或给定值，考察被解释变量的总体均值，即当解释变量取某个确定值时，被解释变量所有可能出现的对应值的平均值。

一元线性回归的参数估计

1普通最小二乘估计（OLS）

高斯—马尔可夫定理(Gauss-Markov theorem)：在给定经典线性回归的假定下，最小二乘估计量是具有最小方差的线性无偏估计量（best linear unbiased estimator, BLUE）

2极大似然估计（MLE）
极大似然估计(Maximum Likelihood Estimation, MLE)的基本原理是，当从模型总体随机 抽取n组样本观测值后，最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大。

3参数估计量的概率分布及随机干扰项方差的估计

一元线性回归模型的检验

1拟合优度检验
拟合优度检验是对回归拟合值与观测值之间拟合程度的一种检验。度量拟合优度的指标主要是判定系数（可决系数）
2变量显著性检验

一元线性回归模型的预测

1点预测
对于拟合得到的一元线性回归模型, 在给定样本以外的解释变量的观测值 ，可以得到被解释变量的预测值，可以此作为其条件均值或个别值的一个近似估计，称之为为点预测。

2区间预测

一元线性回归模型综合案例

10.3多元线性回归

多元线性回归模型的检验

1拟合优度检验
拟合优度检验是对回归拟合值与观测值之间拟合程度的一种检验。度量拟合优度的指标主要是判定系数（可决系数）

2方程总体显著性检验
方程的整体显著性检验，旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断。一般使用F检验。

3单个变量显著性检验

多元线性回归的预测

1单值预测
2区间预测

多元线性回归综合案例

第十一章线性回归模型的扩展

11.1多重共线性

多重共线性的定义和后果

解释变量间存在线性关系。
关于模型中解释变量之间的关系主要有三种：
（1） 解释变量间毫无线性关系，变量间相互正交。
（2）解释变量间完全共线性，此时模型参数将无法估计。
（3） 解释变量间存在一定程度的线性关系。实际中碰到的主要是这种情形。当相关性较弱时，可能影响不大，但是随着解释变量间的共线性程度加强，对参数估计值的准确性、稳定性带来影响。

多重共线性检验

多重共线性的克服

1逐步回归
逐步回归主要分为向前逐步回归（forward）、向后逐步回归(backward)和向后向前逐步回归（both）。逐步回归本身并不是一种新的回归或者参数的估计方法，所用到的参数估计方法都是原来的，是从众多的变量中选出最优模型的变量的一套方法。

2岭回归

11.2异方差

异方差的定义和后果

回归参数估计量不再具有有效性，会对模型的F检验和t检验
带来问题。

异方差性的检验

（一）散点图与残差图
定性分析主要利用散点图和残差图的形状来初步判断异方差的存在性。散点图和残差图呈“喇叭”型分布，说明数据可能存在递增型异方差。但定性分析只能提供一个主观、初略的判断，还需进一步借助更加精确的检验方法。

（二）Goldfeld-Quandt检验
Goldfeld-Quandt检验是Goldfeld-Quandt于1965年提出的，所要检验的问题为具有同方差还是递增型异方差。

（三）Glejser检验
既可以检验递增型异方差，也可以检验递减型异方差。

（四）White检验

异方差性的克服

1广义最小二乘法
2取对数

11.3序列相关性

序列相关性的定义和后果

序列相关性的检验

（一）定性分析法
若残差序列图与图11-15类似，或者残差散点图与图11-16类似，则说明 存在正自相关；若残差序列图与图11-17类似，或者残差散点图与图11-18类似，则说明 存在负自相关。

（二）DW（Durbin-Watson）检验法

序列相关性的克服

序列相关系数的估计

第十二章 非线性回归模型

非线性回归分析是线性回归分析的扩展，由于非线性回归的参数估计涉及非线性优化问题，计算比较困难，因此在计算机诞生前较少研究。20世纪七八十年代以来，随着计算机技术的发展，非线性回归的参数估计计算困难得到了克服，统计推断和预测分析技术也有很大发展。非线性回归分析也开始受到更多的重视，现在已经成为统计学、计量经济学研究的热点之一。

12.2可线性化的非线性回归

Cobb-Douglas生产函数

dat=read.csv(file=“douglas.csv”)
lm1=lm(log(y)~log(x2)+log(x3),data=dat)
summary(lm1)

Call:
lm(formula = log(y) ~ log(x2) + log(x3), data = dat)

Residuals:
Min 1Q Median 3Q Max
-0.15920 -0.02914 0.01179 0.04087 0.09640

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.3385 2.4495 -1.363 0.197939
log(x2) 1.4988 0.5398 2.777 0.016758 *
log(x3) 0.4899 0.1020 4.800 0.000433 ***

Signif. codes:
0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.07481 on 12 degrees of freedom
Multiple R-squared: 0.889, Adjusted R-squared: 0.8705
F-statistic: 48.07 on 2 and 12 DF, p-value: 1.867e-06

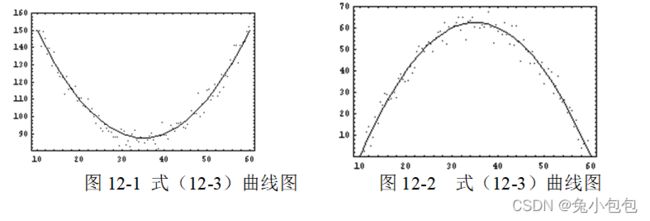
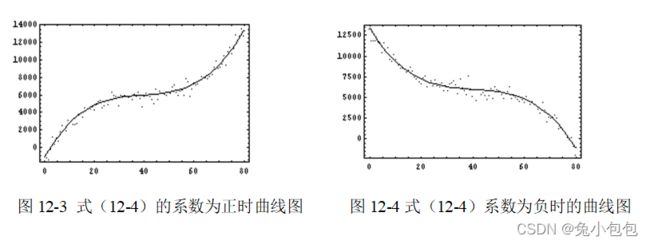
多项式方程模型

x = c(100,200,300,450,600,800,1000)
y = c(253, 337,395,451,495,534,574)
lm.1 = lm(y ~ x) # 一次模型 y=a+bx
lm.2 = lm(y ~ x + I(x^2)) # 二次模型 y=a+bx+cx2
lm.3 = lm(y ~ x + I(x^2) + I(x^3)) # 三次模型 y=a+bx+cx2+dx3
summary(lm.1)$coefEstimateStd.Errortvalue(Intercept)269.466073424.1842101611.142232x0.33412680.041806247.992271Pr(>|t|)(Intercept)0.0001015488x0.0004951455summary(lm.2)$coef
Estimate Std. Error t value
(Intercept) 2.002120e+02 1.695062e+01 11.811481
x 7.061816e-01 7.567631e-02 9.331607
I(x^2) -3.410076e-04 6.754293e-05 -5.048753
Pr(>|t|)
(Intercept) 0.0002940767
x 0.0007341536
I(x^2) 0.0072374199
summary(lm.3)$coefEstimateStd.Errortvalue(Intercept)1.554847e+028.182083e+0019.003076x1.118596e+006.453789e-0217.332397I(x^2)-1.254302e-031.360356e-04-9.220394I(x^3)5.550306e-078.183596e-086.782234Pr(>|t|)(Intercept)0.0003181899x0.0004185186I(x^2)0.0026985540I(x^3)0.0065518838plot(x,y)lines(x,fitted(lm.1),lty=1)lines(x,fitted(lm.2),lty=2)lines(x,fitted(lm.3),lty=3)legend(700,400,c("直线","二次曲线","三次曲线"),lty=1:3)summary(lm.1)$r.squared
[1] 0.9274062
summary(lm.2)$r.squared[1]0.9901534summary(lm.3)$r.squared
[1] 0.9993971

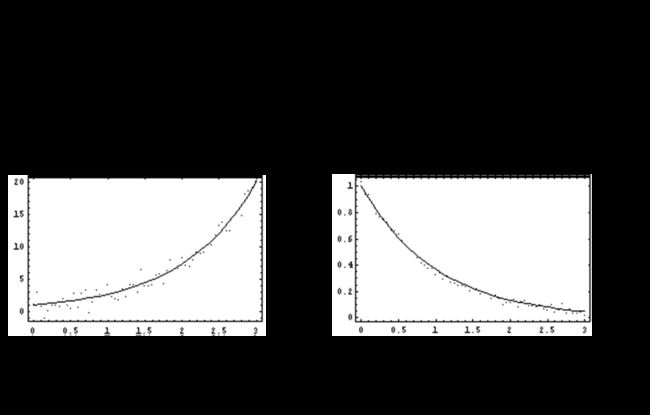
指数函数模型

12.3不可线性化的非线性回归

实际上，非线性最小二乘估计和非线性极大似然估计都是非线性优化的问题，非线性优化有多种算法，比如有格点搜索法、二次爬坡法、高斯牛顿法和牛顿拉夫森法等。

非线性模型的参数估计与迭代算法

初始值选取

在利用迭代算法进行非线性回归参数估计时，初始值的选择是一个值得重视的问题，如果我们想要得到较好的结果和提高工作效率，必须认真对待参数估计值的选择。但参数初始值的选择并没有一般法则。尽量接近参数真实值或最终估计值，最好是参数真实值的一致估计，是正确的初始值选择原则。但该原则的实用价值不大，因为参数真实值不可能知道，而一致估计量正是我们要求出的最小二乘估计量。在实践中，人们常常运用的是如下的经验方法：
１、利用参数的经济意义。
2、模型函数在特定点的性质。
3、降维法。

收敛性

12.4非线性回归评价和假设检验

可决定系数

参数显著性的F检验

似然比检验

第十三章 二元选择模型

前面我们探讨了连续型的因变量建模分析，但实际中，并非所有的变量都是连续型的数据，有时因变量是离散型的数据，这时候我们需要用广义线性模型（generalized linear model, GLM）。
离散因变量（Discrete Dependent Variable）是指取值为0、1、2….等离散值的变量。在多数情况下，这些取值一般没有实际的意义，仅代表某一事件的发生，或者是用于描述某一事件发生的次数。根据取值的特点，离散因变量可以分为二元变量（binary variable）、多分变量和计数变量(count variable)。二元变量的取值一般为1和0，当取值为1时表示某件事情的发生，取值为0则表示不发生，比如信用卡客户发生违约的记为1，不违约的记为0。因变量为二元变量的模型称为二元选择模型(Binary Choice Model)。

13.2线性概率（LP）模型原理

13.3Probit模型原理

Logit模型原理

13.5边际效应分析

13.6最大似然估计（MLE）

13.7似然比检验和拟合优度

13.8案例

13.9扩展案例

第十四章多元选择模型

多分变量所取的离散值个数多于两个，如果各种结果之间没有自然顺序的话，称为无序变量。多分变量为因变量的模型称为多元选择模型(Multinomial Model)，其中又有有序选择模型(Ordered Model)、条件模型(Conditional Model)、嵌套模型(Nested Model)等分类。

14.1有序选择模型

14.2多元无序logit模型

14.3嵌套logit模型

第十五章

计数变量主要用于描述某一事件发生的次数，它仅取整数值。例如，每户家庭的子女数。因变量为计数变量的模型称为计数模型(Count Model)。
受限因变量（limited dependent variable）是指因变量的观测值是连续的，但是受到某种限制，其抽样并非完全随机的，得到的观测值并不完全反应因变量的真实情况。选择性样本（selective sample）是受限因变量的主要形式，其样本观测值是在选择性限制的情况下抽取的。受限因变量常见的两类数据：截断（truncation）数据和审查（Censoring）数据。受限因变量模型主要包括截断模型(Truncated Model)和审查模型(Censored Data)两类。这两类模型多应用在调查数据的分析当中。

15.1计数模型

15.2受限因变量模型

第十六章分位数回归

第十七章高级统计绘图

17.1绘制地图

地图毫无疑问是展示地理信息数据时最直观的工具，尤其是当地图和统计量结合时，其功效则会进一步加强。在本书的第一章中曾经提到过John Snow的地图，注意图中不仅标示出了霍乱发生的地点，每个地点的死亡人数也用点的数目标示了出来。历史上还有不少类似的使用地图的例子，而在今天，地理信息系统(GIS)已经成为研究空间和地理数据的热门工具，地图的应用也是屡见不鲜。
地图的本质是多边形，而多边形的边界则由地理经纬度数据确定。R中的附加包 maps (Brownrigg，2010)是目前比较完善的地图程序包之一，因此本节主要介绍该程序包

17.2高级绘图工具–ggplot2

ggplot2它是一个有着完整的一套图形语法所支持的软件包，其语法基于《Grammar of Graphics》（Wilkinson，2005）一书。该绘图包的特点在于并不去定义具体的图形（如直方图，散点图），而是定义各种底层组件（如线条、方块）来合成复杂的图形，这使它能以非常简洁的函数构建各类图形，而且默认条件下的绘图品质就能达到出版要求。
首先在ggplot2的语法中，有几个概念需要了解：
图层（Layer）：图层允许用户一步步的构建图形，方便单独对图层进行修改、增加、甚至改动数据。
标度（Scale）：标度是一种函数，它控制了数学空间到图形元素空间的映射。一组连续数据可以映射到X轴坐标，也可以映射到一组连续的渐变色彩。一组分类数据可以映射成为不同的形状，也可以映射成为不同的大小。
坐标系统（Coordinate）：坐标轴可以进行变换以满足不同的需要，除直角坐标外还有对数坐标、极坐标等。
位面（Facet）：很多时候需要将数据按某种方法分组，分别进行绘图。位面就是控制分组绘图的方法和排列形式。

散点图

一般对于一系列观测值的图形描述，可以用散点图来直观表达。这里基本的散点图绘制可以使用qplot()函数# 第十八章 如何制作自己的R包
R包提供了一个加载所需代码、数据和文件的集合。R软件自身就包含大约30种不同功能的包，这些基本包提供了R软件的基本功能。与此同时，R作为一个开源软件，它提供了各种统计计算函数，从而方便使用者能够灵活机动的进行数据分析，甚至创造出符合特定需要的新统计计算方法，而这些函数大多是以包的形式提供，这些都是世界各地R用户自己编写的，并上传到网上分享。因此，制作出属于用户自己的R包，并与全世界的R用户共享是一件非常有意思的事情。
library(ggplot2)
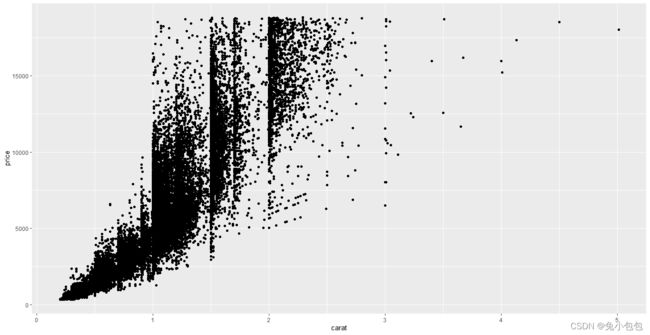
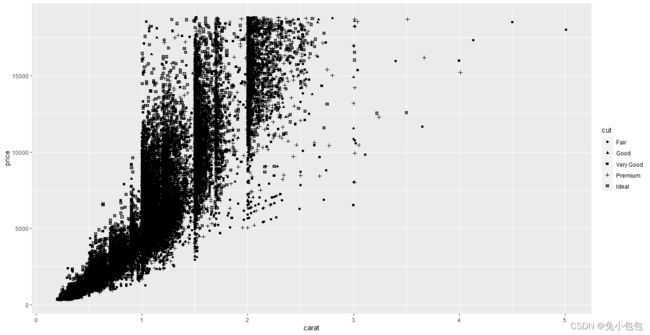
qplot(carat,price,data=diamonds)
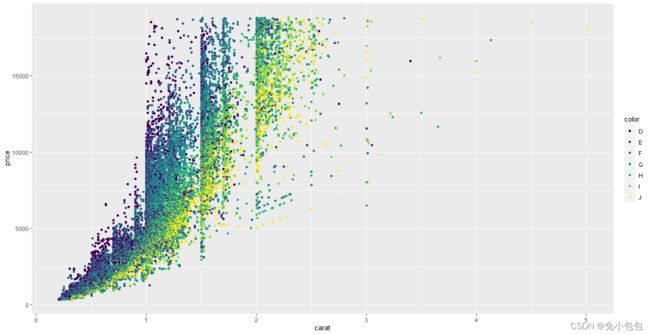
qplot(carat,price,data=diamonds,colour=color)
qplot(carat,price,data=diamonds,shape=cut)
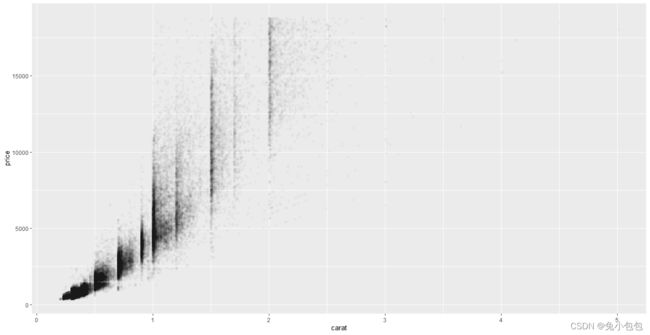
qplot(carat,price,data=diamonds,alpha= I(1/50))
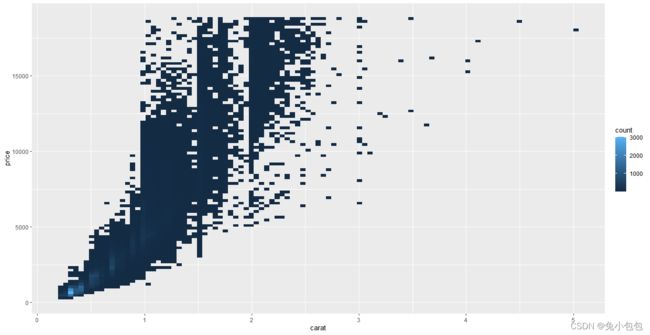
p <- ggplot(diamonds, aes(carat, price))
p + stat_bin2d(bins = 100)

散点图上添加平滑曲线

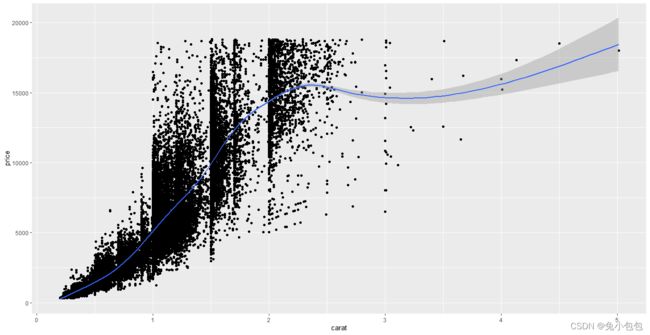
为了展示数据的趋势，一般需要在散点图上面添加一条平滑的曲线。这里可以通过添加smooth对象传递给geom参数，它会将这些图按照顺序进行重叠
qplot(carat,price,data=diamonds,geom=c(“point”,“smooth”))
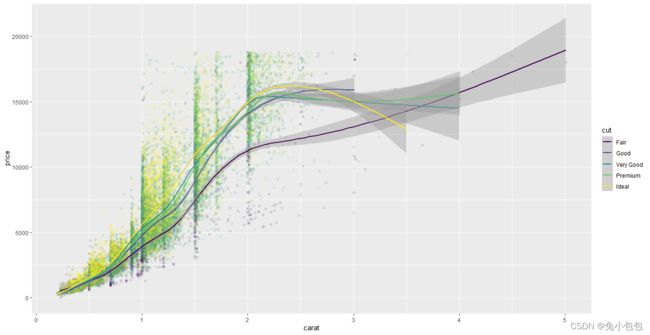
p <- ggplot(diamonds, aes(carat, price,colour=cut))
p + geom_point(alpha=0.1) + geom_smooth()

条形图和箱线图

对于离散型变量，频数一般可以使用条形图来绘制，并且不需要像基础图形下面使用barchart先对数据进行汇总。这里直接使用geom=”bar“即可，并且如果需要对数据分组，可以使用wight来表达。

qplot(color,data=diamonds,geom=“bar”)
qplot(color,data=diamonds,geom=“bar”,weight=carat)+scale_y_continuous(“carat”)
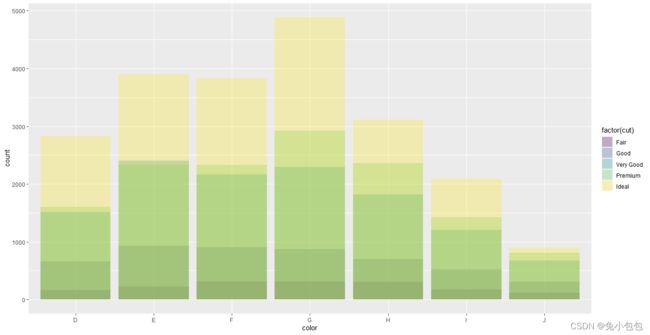
p <- ggplot(data=diamonds,aes(x=color,fill=factor(cut)))
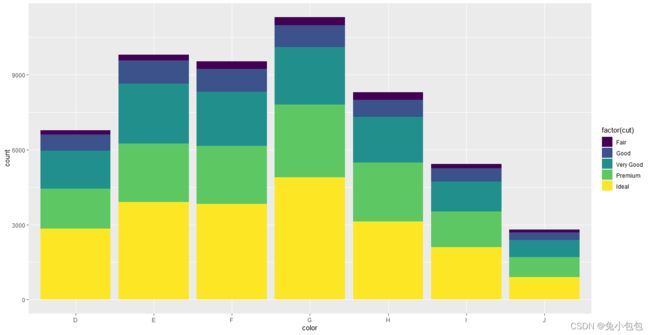
p + geom_bar(position=‘stack’)
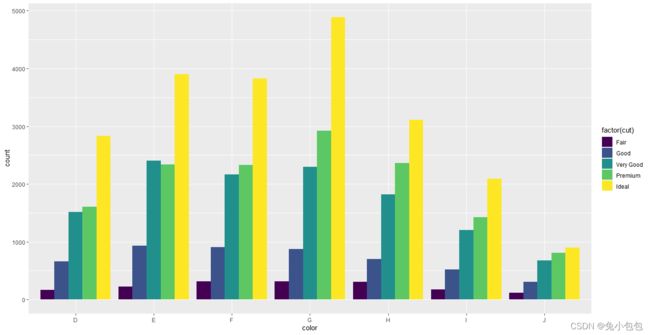
p + geom_bar(position=‘dodge’)
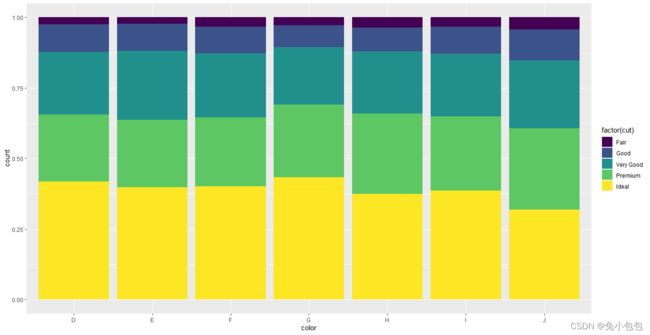
p + geom_bar(position=‘fill’)
p + geom_bar(position=‘identity’,alpha=0.3)


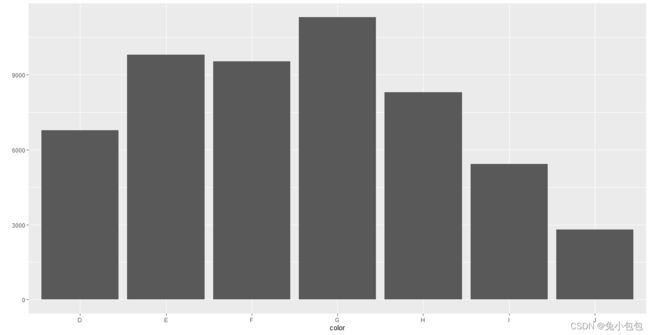
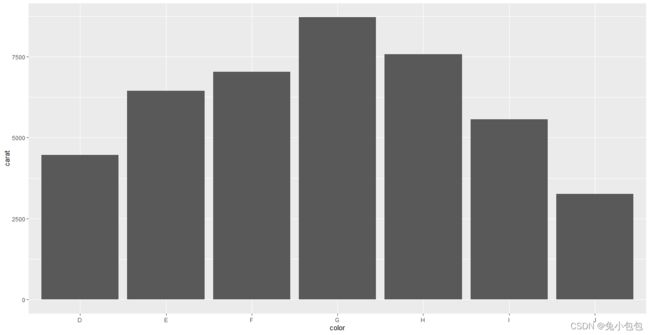
还可以对条形图分组并绘制不同类型的条形图。一般调整的参数有stack、dodge、fill、identity，stack方式是将不同年份数据堆叠放置；dodge方式是将不同年份的数据并列放置；fill方式和stack类似，但Y轴不再是计数，而是以百分比显示；identity方式是不做任何改变直接显示出来，所以需要设置透明度才能看得清楚,默认是stack

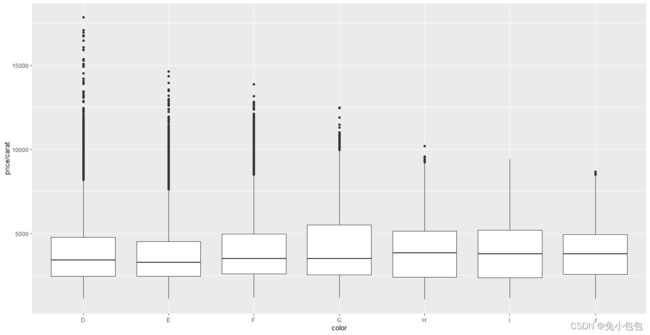
qplot(color,price/carat,data=diamonds,geom=“boxplot”)
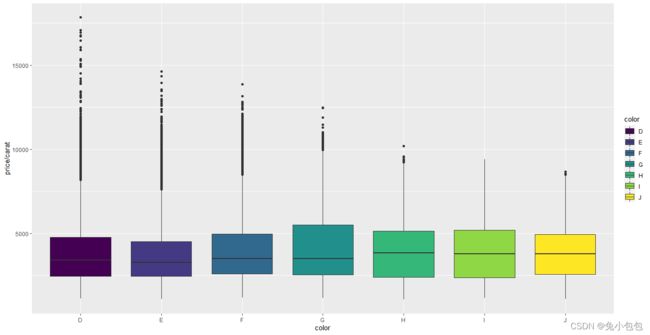
p<- ggplot(diamonds,aes(color,price/carat,fill=color))
p + geom_boxplot()
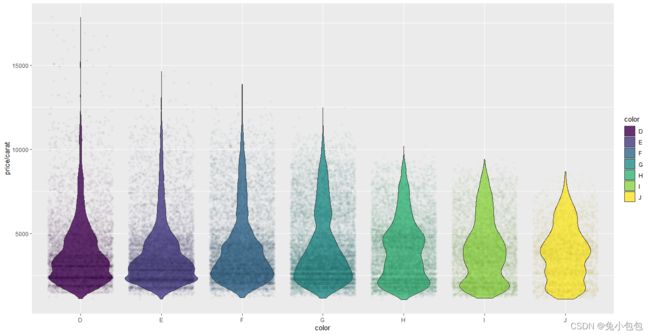
p + geom_violin(alpha=0.8,width=0.9) + geom_jitter(shape= 21, alpha = 0.03)

直方图和密度曲线图

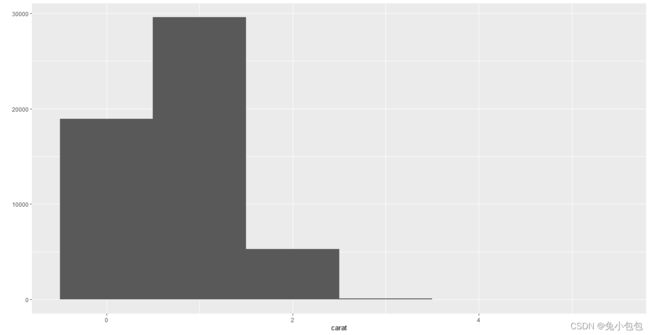
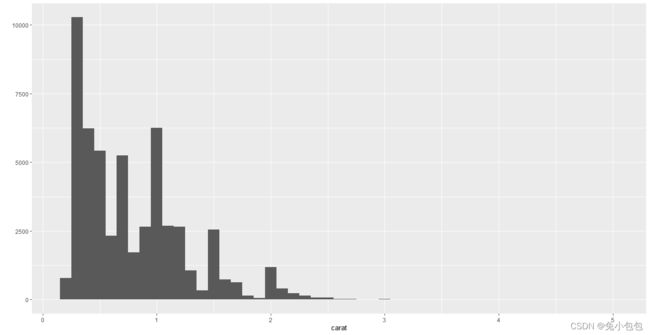
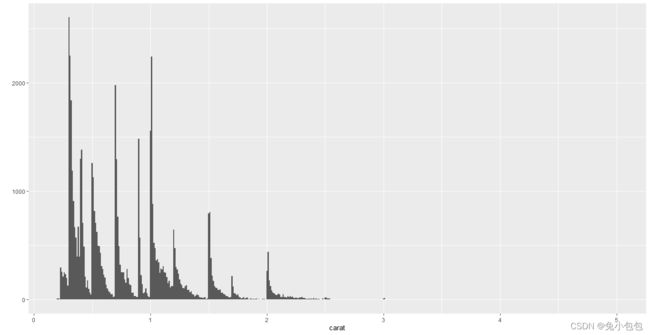
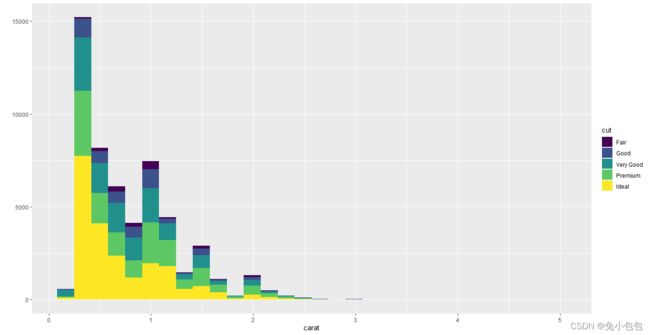
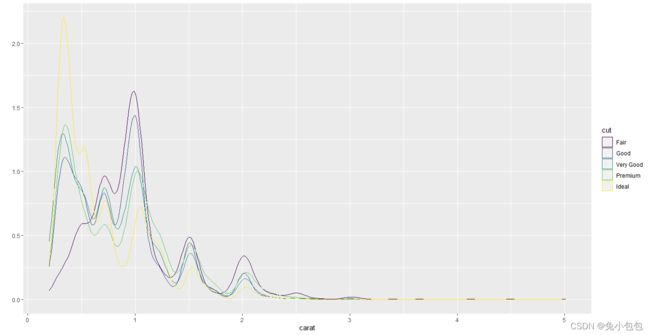
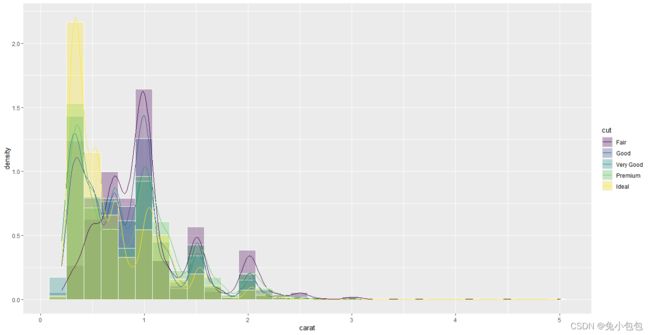
一般对于连续性数据我们会只用直方图或者密度曲线图来绘制。这里只需在qplot()上面添加参数geom=”histogram”和geom=”density”。来进行实现。其中，直方图的组距使用binwidth参数来进行调整，密度曲线的平滑程度则使用adjust参数来进行设定
qplot(carat,data=diamonds,geom=“histogram”,fill=cut)
qplot(carat,data=diamonds,geom=“density”,colour=cut)
p <- ggplot(diamonds, aes(carat))
p + geom_histogram(position = ‘identity’,alpha=0.3,aes(y = …density…,fill = cut),color=“white”) + stat_density(geom = ‘line’, position = ‘identity’, aes(colour = cut))

时间序列图

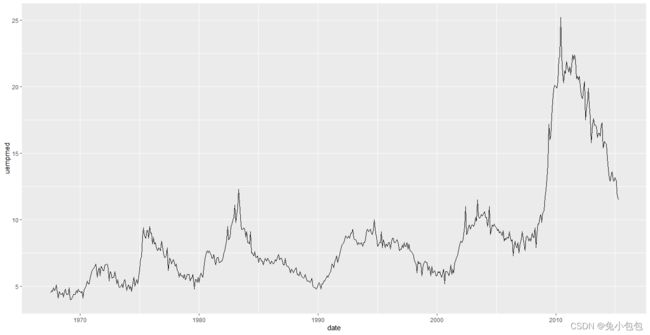
qplot(date,uempmed,data=economics,geom=“line”)

图形标注

unemp <- qplot(date, uempmed, data=economics, geom=“line”)
presidential <- presidential[-(1:3),]
unemp + geom_vline(aes(xintercept = as.numeric(start)), data = presidential)

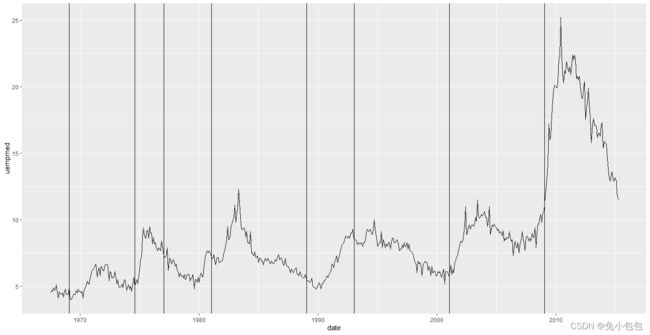
library(scales)
xr <- range(economics$date)yr<-range(economics$uempmed)
unemp + geom_rect(aes(NULL,NULL,xmin=start,xmax=end,fill=name),ymin=yr[1],ymax=yr[2],data=presidential,alpha=0.2)

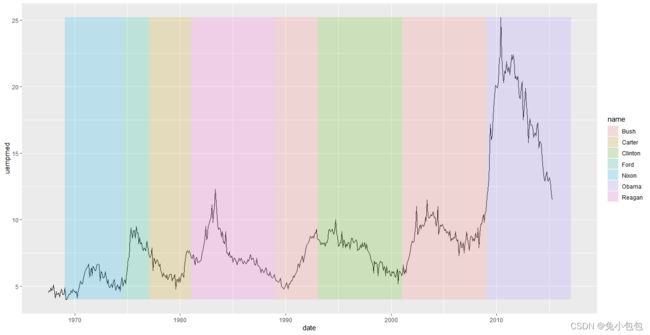
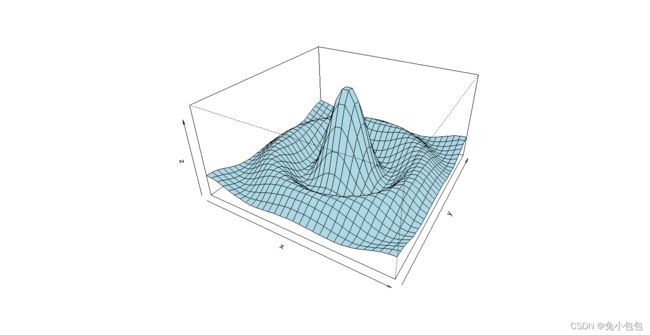
17.3三维图形与等高线图

三维图形

x <- seq(-10, 10, length= 30)
y <- x
f <- function(x, y) { r <- sqrt(x^2+y2); 10 * sin®/r }
z <- outer(x, y, f)
z[is.na(z)] <- 1
op <- par(bg = “white”)
persp(x, y, z, theta = 30, phi = 30, expand = 0.5, col = “lightblue”)

17.4词云

在目前流行的文本挖掘中，词云(world cloud)是一个常用的对文本词汇频次进行表现的形式。一般通过文字字号的大小来表示词频的多少，还可以使用不同颜色加以区分。

17.5散点图矩阵与关系矩阵图

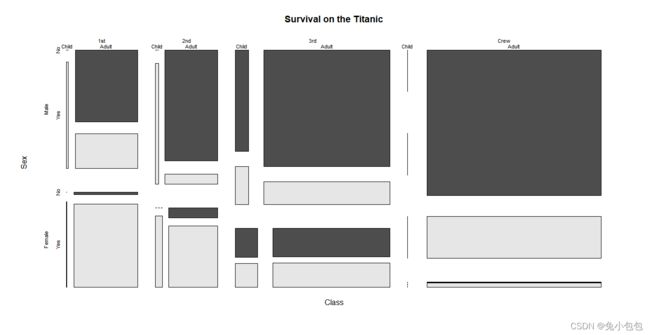
17.6马赛克图

ftable(Titanic)
require(stats)
library(graphics)
mosaicplot(Titanic, main = “Survival on the Titanic”, color = TRUE)

18.1R包基础

| package (包的名字)
|–DESCRIPTION (描述文件，包括包名、版本号、标题、描述、依赖关系等)
|–NAMESPACE (包的命名空间文件)
|–R (函数源码)
|–function1.R
|–function2.R
|–man (帮助文档，存放函数说明文件的目录)
|–function1.Rd
|–Package.Rd

DESCRIPTION包含以下基本内容：
Package: package name /表示包的名称
Type: Package /表示R-Project的类型，R包对应的为“Package”
Title: What the package does (short line) /标题，简要描述R包功能
Version: 1.0 /记录R包的版本信息
Date: when the package is built /记录R包的制作时间
Author: Who wrote it /记录R包的作者
Maintainer: Who to complain to [email protected] /记录R包的维护者
Description: More about what it does (maybe more than one line) /详细描述R包的功能
License: What license is it under? /表示R包的使用许可

包的命名空间NAMESPACE是R包管理包内对象的一个途径，它可以帮助R包的作者控制保内的哪些函数对象是对用户可见的，哪些对象是从别的包导入（import），哪些对象从包中导出（export）。当我们在写一个R包时，有时候会涉及到许多函数，但是其中一些函数可能只是为了方便其它函数的编写而被抽象独立出来的子函数，这些子函数只需要被R包中的其他函数调用，对于外界用户而言并没有什么帮助，因此它们不需要对外界用户可见。NAMESPACE文件就提供了这样一个功能，我们可以通过在包的根目录下创建一个NAMESPACE文件，通过写上export(函数名)来导出那些需要对用户可见的函数。自R 2.14.0开始，所有的R包都必须有命名空间，如果没有的话，R也会自动创建。

R文件夹下存放的是R包中所涉及到的，以.r格式保存的函数源文件。
man文件夹下存放的是Rd文件，也就是R帮助的源代码，一般情况下，R会自动创建与R目录下的函数对应的.Rd文件以及一个额外的用以描述整个R包情况xxx-Package.Rd文件。

18.2在windows中制作R包

1制作R包前的环境配置
首先确保正确安装R软件，RGUI或者Rstudio，注意安装路 径以及软件语言最好选择英文以避免可能因为语言出现的错误。
目前最新版本的RGUI为R-3.0.2，RGUI的下载地址为(厦门大学镜像)：
http://mirrors.xmu.edu.cn/CRAN/bin/windows/base/
目前最新版本的Rstudio为RStudio v0.98，下载地址为：
http://www.rstudio.com/ide/download/
而制作R包的工具软件主要有Rtools，MikTeX或Ctex (如果不需要pdf的帮助手册，则不需要安装)

其中，Rtools是制作R包最重要也是最主要的工具，Rtools包含了windows环境下制作R包的一系列工具，其中包括：
CYGWIN，用以在windows环境模拟UNIX环境。
MinGW编译器，用以编译C和Fortran语言。
Perl编译器，用以编译Perl语言。
最新版本的Rtools的下载地址为(厦门大学镜像)：
http://mirrors.xmu.edu.cn/CRAN/bin/windows/Rtools/

在完成上述软件的安装后，我们需要对文件的启动路径进行设置从而使得可以通过cmd命令行直接调用Rtools等相应软件。
具体操作为：右键点击计算机>属性>高级系统设置>环境变量>系统变量 PATH一项，点击“编辑”，检查是否具有以下路径。通常软件在安装时已经自动配置好了启动路径。如果没有，需要手工添加，如图18-1所示
在完成上述步骤之后，打开cmd命令行窗口，输入R cmd –help 以检测R环境是否成功配置，正确配置后返回的结果如图18-2所示

2编写R程序
在Windows下编写R程序包通常包括以下几步：
①编写.r函数源代码，也就是用来生成R程序包的函数脚本。
在本文的演示中，假如现在我们已经有了一个编好的R函数Hello，用来在屏幕上输出问候：
hello<-function(name)
{
print(paste(“Hello”,name))
}
存成了r脚本的格式,文件名为Hello.r
②利用R软件自带的package.skeleton()函数，生成R包中的Description 文件和帮助文件.rd。
③按要求填写生成的Description 文件和帮助文件.rd
④在windows cmd的命令行中输入相应的命令，生成zip文件或者.tar.gz,并进行相应的检查。

18.3 在RStudio中制作R包

打开Rstudio，利用左上方的菜单，Rstudio>File>New Project，打开新项目。选择New Directory为待创建的R包建立新的工作路径，选择R package，如图18-5所示。
在接下来的操作页面中输入与R包有关的信息，如包名，源文件链接，以及创建R包的工作路径，如图18-6所示
填选上述信息之后，点击“Creat Project”，在右下角展开如下工作页面，如图18-7所示
可直接点选对应的文件，打开编辑窗口编辑文件内容，文件的格式要求与前文一致，如图18-8所示。
在编辑好DESCRIPTION，hello.Rd，hello-package.Rd等文件后。点击Build按钮，如图18-9所示。
Build & Reload 和 Check 选项提供了 R CMD的可视化操作，点选Check之后就相当于执行了Rcmd的 build 和 check 指令。执行结果将会显示于菜单下方窗口，如图18-10所示。
最后，我们会在先前创建工程时设定好的工作路径下找到被创建好的R包。将R包载入后执行得到如下结果：

library(hello)
hello(“world”)
[1] “Hello world”