深度学习入门-基于python的理论与实现（五）误差反向传播法

回顾

上一章中我们介绍了神经网络的学习，并通过梯度下降法来实现最优参数，但是计算量大，耗费时间，误差反向传播法能够高效计算权重参数。我们先通过计算图来理解这个概念，然后通过数学式加深理解。

1 计算图

上面的称为正向传播，与之对应的就是反向传播。

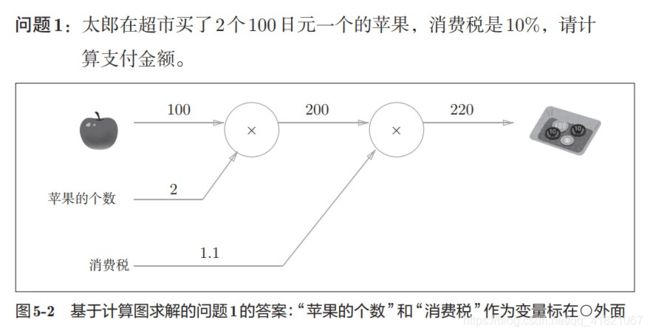
1.1局部计算

局部计算就是不关心之前的 数字是怎么来的，只要把两个数字相加就可以了。
例如我们买了100个苹果，和其他4000元的东西，我们不需要知道4000是怎么来的，把4000和苹果的价钱相加就可。
局部计算把复杂的全局计算分解。

1.2 计算图的优点是什么

1）局部计算可以简化全局计算
2）可以保存计算过程中的数据
3）也就是今天要引入的反向传播，通过计算图的反向传播来计算导数。

1.3 反向传播的导数是怎么求？

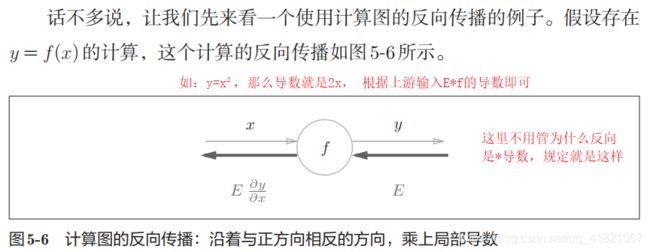
上面是通过链式法则来求得的，什么是链式法则？

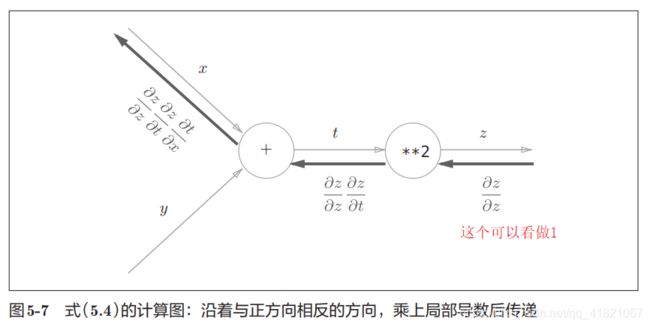
之前学过高等数学的时候也讲过这个，

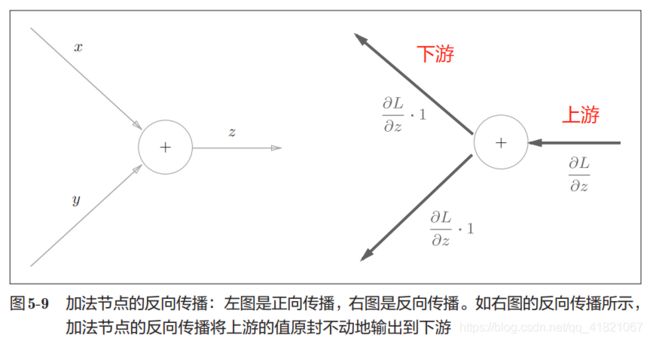
1.3.1加法节点的反向传播

所以加法节点的反向传播就是直接乘1

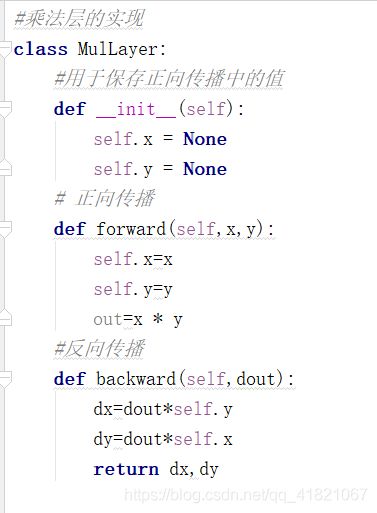
1.3.2 乘法节点的反向传播

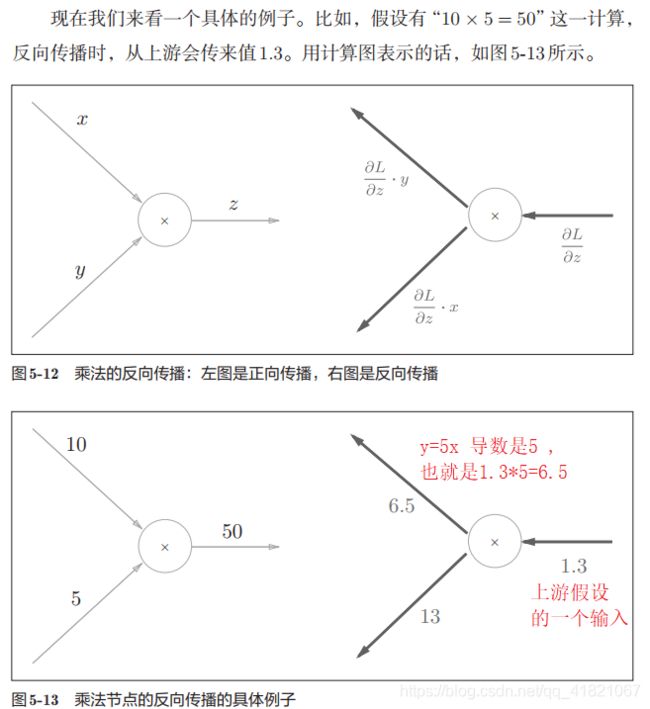
所以乘法节点的反向传播就是乘以另一边的值，也就是对向相乘输出，
1.35=6.5
1.310=13

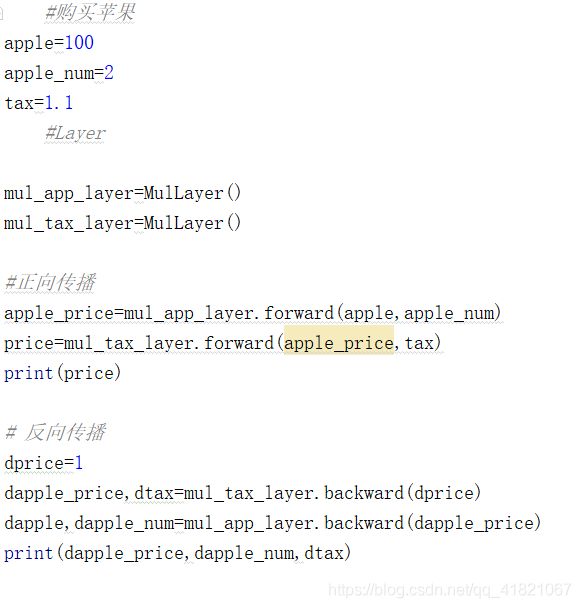
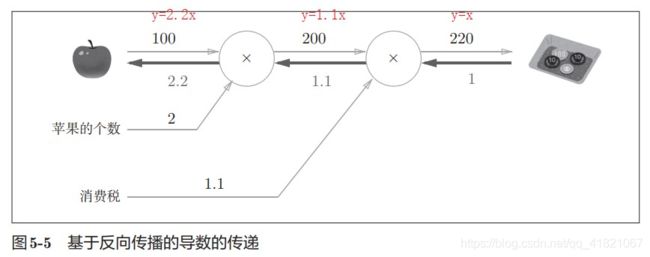
1.3.3 购买苹果的反向传播

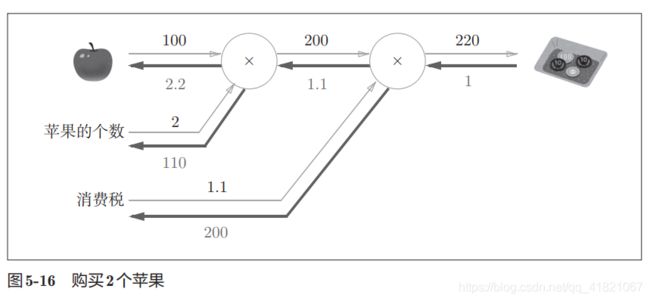
其中根据乘法的反向传播可以知道1.12=2.2
1.1100=110。

1.3.4神经网络中层的概念

我们可以知道，层是神经网络中的功能单位，如sigmod,Affine,都是用层来进行实现的，所以实现乘法节点的是乘法层，实现加法节点的是加法层。

2 简单层的实现

2.1参数

forward:正向传播
backward:反向传播

2.2 乘法层的实现-购买两个苹果实例

用上面类中的方法实现购买苹果

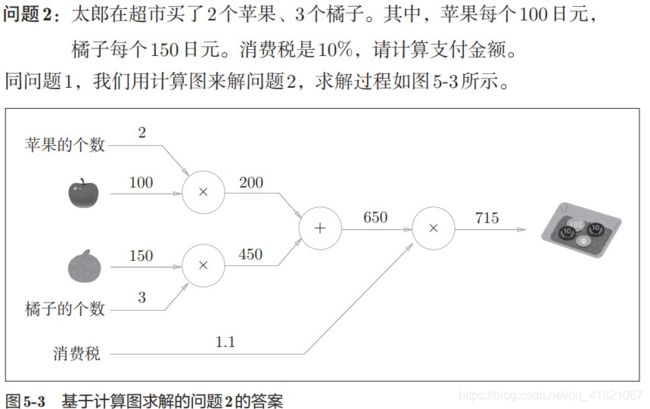
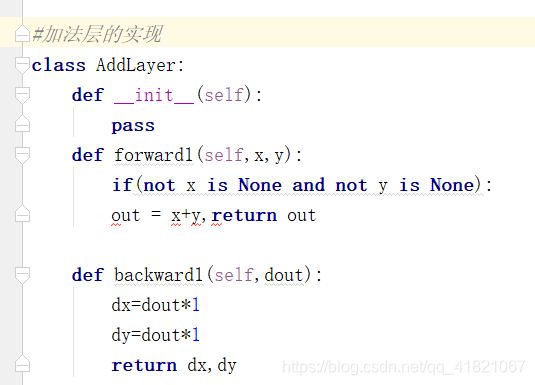
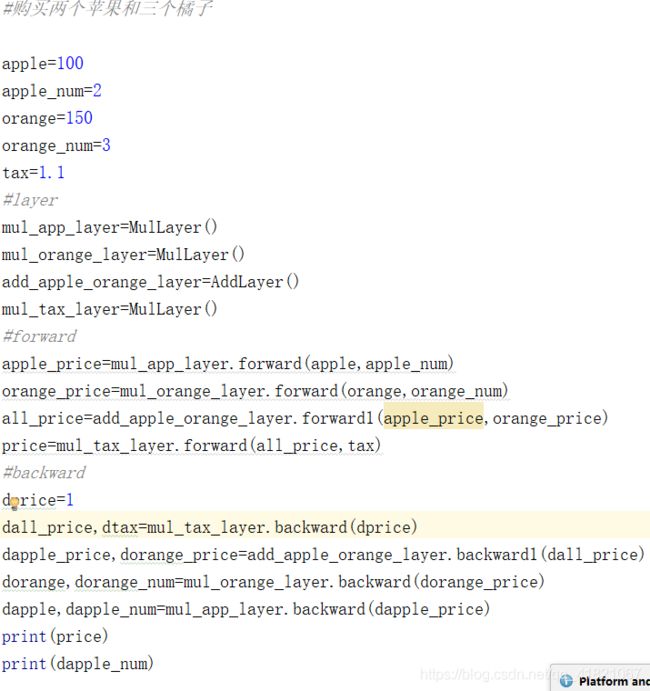
2.3加法层实现-购买两个苹果和三个橘子实例

将计算图的思想应用到神经网络中，把构成神经网络的层看为一个实现类，先来看激活函数的ReLu层和Sigmoid层

2.4 ReLu层

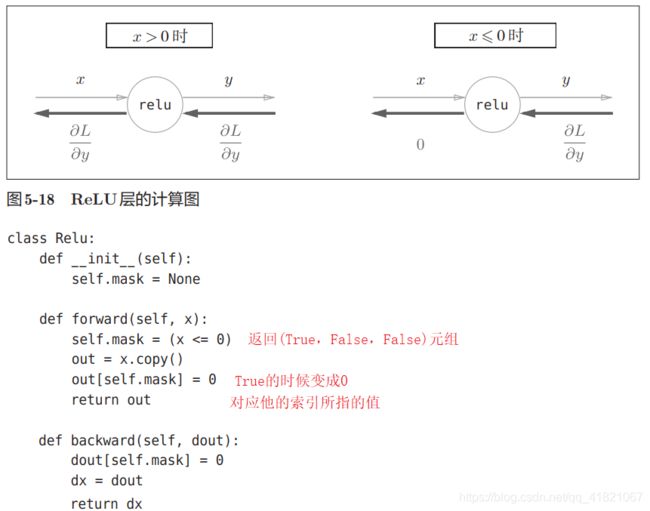
在上面的代码中。如果x<=0就为TRUE，x>0就为False,当为TRUE的时候就输出为0，也就是当x<=0的时候输出为0，当x>0 的时候输出x。

参数

mask.是一个值为TRUE或者FALSE的数组，当x<=0的时候保存为TRUE，当x>0的时候保存为FALSE。

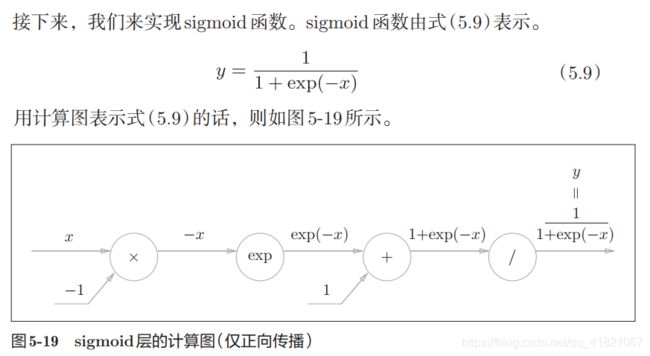
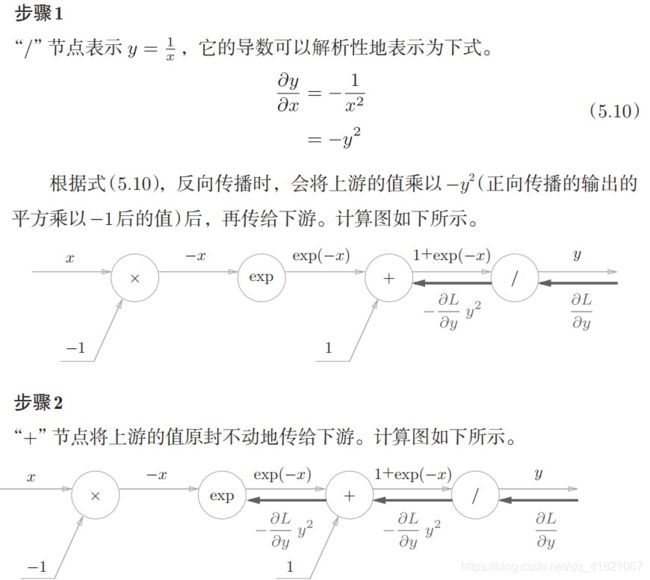
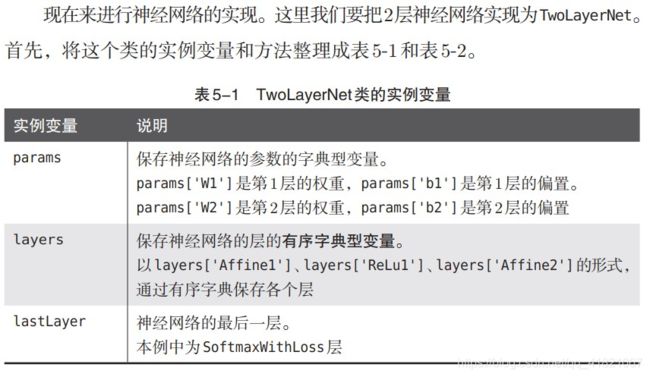
2.5 sigmoid层

2.6 Affine/Softmax层的实现

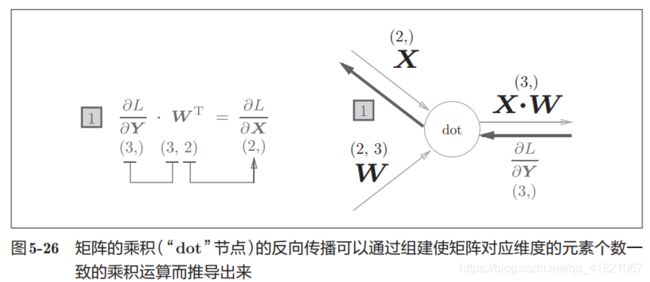
2.6.1 Affine层

神经网络正向传播的计算称为‘’仿射变换‘’，这里将仿射变换称为Affine层
其实就是神经网络中的隐藏层，




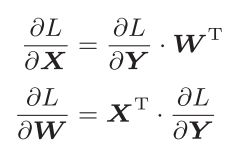
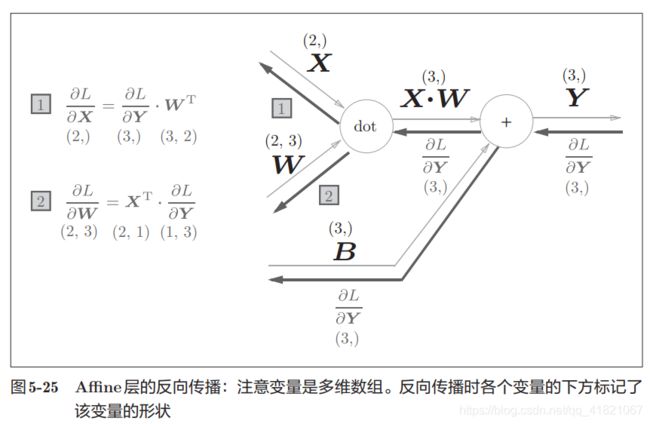
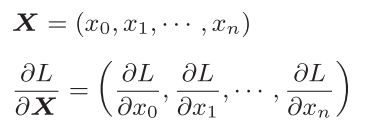
这里要注意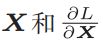
的形状是相同的，这样的话才可以乘积运算。

2.6.2 多个变量输入的Affine层

2.6.3 Softmax-with-Loss层

softmax函数就是将输出正规化后再输出（加起来之和为1），平时不使用，在计算反向传播的时候是要用到的。

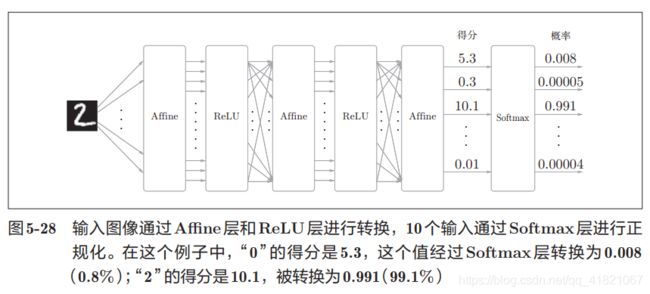
因为在这里考虑到损失函数的交叉熵误差，所以称为Softmax-with-Loss层，计算图如下：

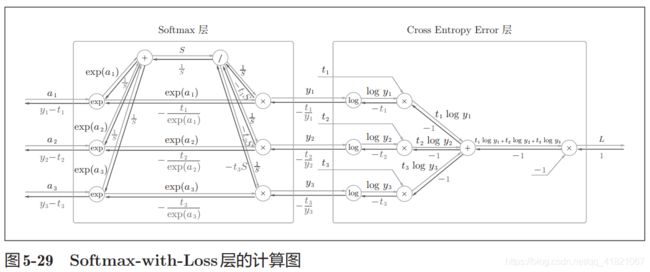
上图因为复杂只给出了结果，如图先用softmax将输入值正规化，然后交叉熵层接收，输出损失L。
下面是简化 的计算图。

在反向传播是（y1-t1,y2-t2,y3-t3）这样的结果，其中t是监督数据，在神经网络的学习过程中我们是为了得到最优。也就是使得输出y 接近监督数据t ,这里反向传播就会告诉神经网络的前一层，也就是神经网络的学习。
在上面的过程中不必纠结反向传播的值是怎么得到的，我们只需要知道可以根据yi-ti来计算梯度。

小结

Affine层计算的是隐藏层的梯度，Softmax-with-Loss层计算的是输出层的梯度

3 误差反向传播的实现

神经网络学习的步骤
1）从训练数据中选出一部分数据
2） 计算损失函数各个权重参数的梯度
3）将权重参数沿着梯度的方向进行更新
4）重复1,2，3步骤

之前的微分可以求得梯度函数，也是时间复杂度高，用误差反向传播就可以快速高效的计算梯度。

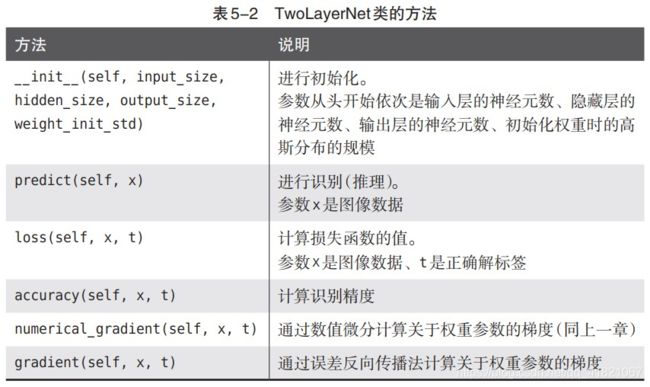
在这里我们实现神经网络就要用到之前的两层神经网络类：TwoLayerNet

这里把梯度的计算改为反向传播
先导入有序字典

根据字典的顺序逐一计算正向传播值

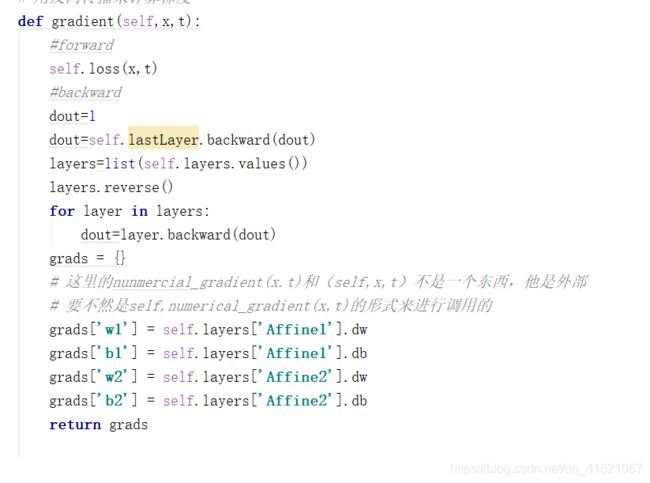
反向传播的上泳默认为1，然后逐一计算反向传播值。

3.1 误差反向传播的梯度确认

利用上一节求得的数学公式求解后的梯度（正确）和误差反向传播求解后的梯度值来做一个对比。

计算后的误差几乎为0，所以说反向传播计算的梯度是正确的。

3.2使用误差反向传播法的反向学习

不同的就是通过误差反向传播求梯度这个

总结

先介绍计算图，利用计算图介绍了神经网络中的误差反向传播法，通过各个层的实现来构成一个神经网络，使用层来进行模块化，神经网络中可以自由组装层，构架个性化网络。