DL-Pytorch-notes 01

基本概念

训练集、测试集、验证集

训练集是用来训练模型内参数的数据集。
验证集用于在训练过程中检验模型的状态，收敛情况。验证集通常用于调整超参数，根据几组模型验证集上的表现决定哪组超参数拥有最好的性能。同时验证集在训练过程中还可以用来监控模型是否发生过拟合，一般来说验证集表现稳定后，若继续训练，训练集表现还会继续上升，但是验证集会出现不升反降的情况，这样一般就发生了过拟合。所以验证集也用来判断何时停止训练，训练集会被多次使用以调参。
测试集用来评价模型泛化能力，即之前模型使用验证集确定了超参数，使用训练集调整了参数，最后使用一个从没有见过的数据集来判断这个模型是否Work，测试集只使用一次。

训练集比作学生的课本，学生根据课本里的内容来掌握知识；验证集比作作业，通过作业可以知道不同学生学习情况、进步的速度快慢；测试集比作考试，考的题是平常都没有见过，考察学生举一反三的能力。
一般来说，我们把数据分成这样的三份：训练集（60%），验证集（20%），测试集（20%）。验证集不是必须的。

损失函数

损失函数用于衡量模型输出的估计值与真实值之间的误差，通常会选取一个非负数作为误差，且数值越小表示误差越小，一个常用的选择是平方函数。

优化算法

当模型和损失函数形式较为简单时，上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解（analytical solution）。本节使用的线性回归和平方误差刚好属于这个范畴。然而，大多数深度学习模型并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解（numerical solution）。
小批量随机梯度下降（mini-batch stochastic gradient descent）在深度学习中被广泛使用。它的算法很简单：先选取一组模型参数的初始值，如随机选取；接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量（mini-batch）BB，然后求小批量中数据样本的平均损失有关模型参数的导数（梯度），最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。

线性回归输出是一个连续值，因此适用于回归问题；softmax回归的输出是离散值，因此适用于分类问题，两者都是单层神经网络。

线性回归的神经网络及代码实现

    def stop(self):
        # stop the timer and record time into a list
        self.times.append(time.time() - self.start_time) #.append用于在self.times列表中添加一个元素
        return self.times[-1]

这是一个计时器的定义片段，.append()用于在类中self.times 列表添加一个元素。

线性回归模型的从零开始的实现

w.requires_grad_(requires_grad=True) 
b.requires_grad_(requires_grad=True) #权重和偏差的初始化

# training
for epoch in range(num_epochs):  # training repeats num_epochs times
    # in each epoch, all the samples in dataset will be used once
    
    # X is the feature and y is the label of a batch sample
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()  
        # calculate the gradient of batch sample loss 
        l.backward()  
        # using small batch random gradient descent to iter model parameters
        sgd([w, b], lr, batch_size)  
        # reset parameter gradient
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

对一个数据将其属性.requires_grad设置为True，它将开始追踪(track)在其上的所有操作（这样就可以利用链式法则进行梯度传播了）。完成计算后，可以调用对结果数据调用.backward()来完成所有梯度计算，对被求导数据调用如b.grad获得以上一系列运算中关于改变量的梯度，也即此Tensor的梯度将累积到.grad属性中。需要注意的是，每一次运行反向传播，梯度都会累加之前的梯度，所以一般在反向传播前需要将梯度清零，操作如b.grad.data.zero_()。

线性回归模型使用pytorch的简洁实现

import torch
from torch import nn
import numpy as np
torch.manual_seed(1)

print(torch.__version__)
torch.set_default_tensor_type('torch.FloatTensor')

torch.manual_seed(1)用于设计随机初始化种子的，要知道神经网络都需要初始化，那么怎么初始化才能保证每次初始化之后都相同，这时候使用同样的随机初始化种子就可以保证。
读取数据集

import torch.utils.data as Data

batch_size = 10

# combine featues and labels of dataset
dataset = Data.TensorDataset(features, labels)

# put dataset into DataLoader
data_iter = Data.DataLoader(
    dataset=dataset,            # torch TensorDataset format
    batch_size=batch_size,      # mini batch size
    shuffle=True,               # whether shuffle the data or not
    num_workers=2,              # read data in multithreading
)

torch.utils.data是pytorch用于实现数据自由读取的一个包，Data.TensorDataset用于把数据放在数据库中，Data.DataLoader用于从数据库中每次抽出batch size个样本进行训练，shuffle=True表示抽取数据是随机的。
定义模型

class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()      # call father function to init 
        self.linear = nn.Linear(n_feature, 1)  # function prototype: `torch.nn.Linear(in_features, out_features, bias=True)`

    def forward(self, x):
        y = self.linear(x)
        return y
    
net = LinearNet(num_inputs)
print(net)

首先，关于python类的一些相关知识可以查看：python类，而本例用的是一个继承类的方法，class LinearNet(nn.Module):表明线性网络是继承自nn.Module这个父类，并且在子类中如果重写了__init__ 时，要继承父类的构造方法，可以使用 super关键字，如super(子类，self).__init__(参数1，参数2，....),详情见子类继承父类初始化。
如果有多层网络叠加，可以使用.Sequential()来定义模型，如下：

# ways to init a multilayer network
# method one
net = nn.Sequential(
    nn.Linear(num_inputs, 1)
    # other layers can be added here
    )

# method two
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......

# method three
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
          ('linear', nn.Linear(num_inputs, 1))
          # ......
        ]))

初始化模型参数

from torch.nn import init

init.normal_(net[0].weight, mean=0.0, std=0.01)
init.constant_(net[0].bias, val=0.0)  # or you can use `net[0].bias.data.fill_(0)` to modify it directly

初始化模型参数详情见pytorch nn.init参数初始化方法。
定义损失函数和优化函数

loss = nn.MSELoss()    # nn built-in squared loss function
                       # function prototype: `torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')`

import torch.optim as optim

optimizer = optim.SGD(net.parameters(), lr=0.03)   # built-in random gradient descent function
print(optimizer)  # function prototype: `torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)`

训练

num_epochs = 3
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        output = net(X)
        l = loss(output, y.view(-1, 1))
        optimizer.zero_grad() # reset gradient, equal to net.zero_grad()
        l.backward()
        optimizer.step()
    print('epoch %d, loss: %f' % (epoch, l.item()))

训练步骤为：确定超参数（训练周期为3，优化学习率为0.03），从数据库中提取批次数据，网络输出，计算损失函数，优化器梯度清零，反向求导，优化参数。

softmax回归的神经网络及代码实现

既然分类问题需要得到离散的预测输出，一个简单的办法是将输出值$o_i$当作预测类别是$i$的置信度，并将值最大的输出所对应的类作为预测输出，即输出 $\underset{i}{\mathrm{argmax}}{o}_i$。例如，如果$o_1,o_2,o_3$分别为$0.1,10,0.1$，由于$o_2$最大，那么预测类别为2。
那么直接使用输出层的输出有两个问题：
1. 一方面，由于输出层的输出值的范围不确定，我们难以直观上判断这些值的意义。例如，刚才举的例子中的输出值10表示“很置信”图像类别为猫，因为该输出值是其他两类的输出值的100倍。但如果$o_1=o_3=10^3$，那么输出值10却又表示图像类别为猫的概率很低。
2. 另一方面，由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。
因此，引入softmax函数可以解决以上问题它通过下式将输出值变换成值为正且和为1的概率分布：

$${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3=\text{softmax}(o_1,o_2,o_3)$$

其中

$$\hat{y}1=\frac{\exp (o_1)}{{\sum }_{i=1}^3\exp (o_i)},\hat{y}2=\frac{\exp (o_2)}{{\sum }_{i=1}^3\exp (o_i)},\hat{y}3=\frac{\exp (o_3)}{{\sum }_{i=1}^3\exp (o_i)}.$$

容易看出${\hat{y}}_1+{\hat{y}}_2+{\hat{y}}_3=1$且$0\le {\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3\le 1$，因此${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3$是一个合法的概率分布。这时候，如果${\hat{y}}_2=0.8$，不管${\hat{y}}_1$和${\hat{y}}_3$的值是多少，我们都知道图像类别为猫的概率是80%。此外，我们注意到

$$\underset{i}{\mathrm{argmax}}{o}_i=\underset{i}{\mathrm{argmax}}{\hat{y}}_i$$

因此softmax运算不改变预测类别输出。
此处采用交叉熵损失函数，假设训练数据集的样本数为$n$，交叉熵损失函数定义为
$$\ell (\mathbf{\Theta })=\frac{1}{n}\sum _{i=1}^{n}H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right),其中H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)=-\sum _{j=1}^q{y}_j^{(i)}\log {\hat{y}}_j^{(i)},$$

其中$\mathbf{\Theta }$代表模型参数。同样地，如果每个样本只有一个标签，那么交叉熵损失可以简写成$\ell (\mathbf{\Theta })=-(1/n){\sum }_{i=1}^n\log {\hat{y}}_{y^{(i)}}^{(i)}$。从另一个角度来看，我们知道最小化$\ell (\mathbf{\Theta })$等价于最大化$\exp (-n\ell (\mathbf{\Theta }))={\prod }_{i=1}^n{\hat{y}}_{y^{(i)}}^{(i)}$，即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。

获取Fashion-MNIST训练集和读取数据

这里会使用torchvision包，它是服务于PyTorch深度学习框架的，主要用来构建计算机视觉模型。torchvision主要由以下几部分构成：

1. torchvision.datasets: 一些加载数据的函数及常用的数据集接口；
2. torchvision.models: 包含常用的模型结构（含预训练模型），例如AlexNet、VGG、ResNet等；
3. torchvision.transforms: 常用的图片变换，例如裁剪、旋转等；
4. torchvision.utils: 其他的一些有用的方法。
   get dataset

mnist_train = torchvision.datasets.FashionMNIST(root='/home/kesci/input/FashionMNIST2065', train=True, download=True, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='/home/kesci/input/FashionMNIST2065', train=False, download=True, transform=transforms.ToTensor())

class torchvision.datasets.FashionMNIST(root, train=True, transform=None, target_transform=None, download=False)

• root（string）– 数据集的根目录，其中存放processed/training.pt和processed/test.pt文件。
• train（bool, 可选）– 如果设置为True，从training.pt创建数据集，否则从test.pt创建。
• download（bool, 可选）– 如果设置为True，从互联网下载数据并放到root文件夹下。如果root目录下已经存在数据，不会再次下载。
• transform（可被调用 , 可选）– 一种函数或变换，输入PIL图片，返回变换之后的数据。如：transforms.RandomCrop。
• target_transform（可被调用 , 可选）– 一种函数或变换，输入目标，进行变换。

其余均类似线性网络进行训练操作，不过训练过程中需要将$28\ast 28$的图像展平为$1\ast 784$的数据向量进行训练。
训练过程中有个函数需要了解一下：view()函数，以二维数组为例：
a.view(-1)表示将数组a的数据展成一个行向量，a.view(-1，n)表示先确定$a$有n列，-1处代表对应计算出的行数，同理，a.view(n,-1)表示先确定$a$有n行，-1处代表对应计算出的列数。

多层感知机

如果多层感知机的每层都是仿射变换的话，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络，即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价，因此需要在隐藏层引入激活函数（非线性）。
多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号，多层感知机按以下方式计算输出：

$$\begin{array}{rl}\mathbf{H}& =\varphi (\mathbf{X}{\mathbf{W}}_h+{\mathbf{b}}_h),\\ \mathbf{O}& =\mathbf{H}{\mathbf{W}}_o+{\mathbf{b}}_o,\end{array}$$

其中$\varphi$表示激活函数。

多层感知机pytorch实现

与线性回归和softmax回归最大的区别在于网络的模型：

num_inputs, num_outputs, num_hiddens = 784, 10, 256
    
net = nn.Sequential(
        d2l.FlattenLayer(),
        nn.Linear(num_inputs, num_hiddens),
        nn.ReLU(),
        nn.Linear(num_hiddens, num_outputs), 
        )
    
for params in net.parameters():
    init.normal_(params, mean=0, std=0.01)

训练

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,root='/home/kesci/input/FashionMNIST2065')
loss = torch.nn.CrossEntropyLoss()

optimizer = torch.optim.SGD(net.parameters(), lr=0.5)

num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)

文本预处理

文本是一类序列数据，一篇文章可以看作是字符或单词的序列，本节将介绍文本数据的常见预处理步骤，预处理通常包括四个步骤：

1. 读入文本
2. 分词
3. 建立字典，将每个词映射到一个唯一的索引（index）
4. 将文本从词的序列转换为索引的序列，方便输入模型

读入文本

import collections
import re

def read_time_machine():
    with open('/home/kesci/input/timemachine7163/timemachine.txt', 'r') as f:
        lines = [re.sub('[^a-z]+', ' ', line.strip().lower()) for line in f]
    return lines


lines = read_time_machine()
print('# sentences %d' % len(lines))

with open('/home/kesci/input/timemachine7163/timemachine.txt', 'r') as f:中open打开文本文件并创建类型为f（可迭代）；
strip()方法用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列；
lower()将大写字母变换为小写字母；
re.sub(pattern, repl, string, count=0, flags=0)pattern：表示正则表达式中的模式字符串；repl：被替换的字符串（既可以是字符串，也可以是函数）；string：要被处理的，要被替换的字符串；count：匹配的次数, 默认是全部替换；flags：具体用处不详。
因此这一段读取文本命令操作为：先将每行文本的空格或者换行符去除，之后将文本中的大写字母全部变换为小写字母，最后将变换后的文本中非小写英文字母的字符串替换为空格。

分词

def tokenize(sentences, token='word'):
    """Split sentences into word or char tokens"""
    if token == 'word':
        return [sentence.split(' ') for sentence in sentences]
    elif token == 'char':
        return [list(sentence) for sentence in sentences]
    else:
        print('ERROR: unkown token type '+token)

tokens = tokenize(lines)
tokens[0:2]

Out[2]
[['the', 'time', 'machine', 'by', 'h', 'g', 'wells', ''], ['']]

定义了一个函数tokenize(sentences, token='word'):，sentences是个列表，列表中的每个元素是个句子，token='word'token是个标志，指代要做哪一个级别的分词，此处word指代要做单词级别的分词；所以如果做单词级别的分词，就在每个sentence的单词之间用空格符分开，如果做字符级别的分词，就直接把字符串转换为一个列表。

用现有方法分词

text = "Mr. Chen doesn't agree with my suggestion."

用spaCy方法分词
详情见spaCy自然语言处理
通过加载模型来创建一个pipeline。 Spacy 提供了许多不同的模型 , 模型中包含了语言的信息- 词汇表，预训练的词向量，语法和实体。
下面将加载默认的模型 english-core-web。nlp 对象将要被用来创建文档，访问语言注释和不同的 nlp 属性，相当于一个pipeline，根据这个pipeline来对text进行分词操作。

import spacy
nlp = spacy.load('en_core_web_sm')
doc = nlp(text)
print([token.text for token in doc])

输出结果：

['Mr.', 'Chen', 'does', "n't", 'agree', 'with', 'my', 'suggestion', '.']

用NLTK方法分词
在NLTK包中有个用于分词的函数 word_tokenize，将要分词的文本载入后对该文本使用word_tokenize函数即可完成分词操作。

from nltk.tokenize import word_tokenize
from nltk import data
data.path.append('/home/kesci/input/nltk_data3784/nltk_data')
print(word_tokenize(text))

输出结果：

['Mr.', 'Chen', 'does', "n't", 'agree', 'with', 'my', 'suggestion', '.']

语言模型

一段自然语言文本可以看作是一个离散时间序列，给定一个长度为$T$的词的序列$w_1,w_2,\dots ,w_T$，语言模型的目标就是评估该序列是否合理，即计算该序列的概率：
$$\begin{array}{rl}P\left(w_1,w_2,\dots ,w_T\right)& =\prod _{t=1}^{T}P\left(w_t|w_1,\dots ,w_{t-1}\right)\\ & =P\left(w_1\right)P\left(w_2|w_1\right)\cdots P\left(w_T|w_1{w}_2\cdots w_{T-1}\right)\end{array}$$
例如，一段含有4个词的文本序列的概率
$$P\left(w_1,w_2,w_3,w_4\right)=P\left(w_1\right)P\left(w_2|w_1\right)P\left(w_3|w_1,w_2\right)P\left(w_4|w_1,w_2,w_3\right)$$
语言模型的参数就是词的概率以及给定前几个词情况下的条件概率。设训练数据集为一个大型文本语料库，如维基百科的所有条目，词的概率可以通过该词在训练数据集中的相对词频来计算，例如，$w_1$的概率可以计算为：

$$\hat{P}\left(w_1\right)=\frac{n\left(w_1\right)}{n}$$

其中$n(w_1)$为语料库中以$w_1$作为第一个词的文本的数量，$n$为语料库中文本的总数量。

类似的，给定$w_1$情况下，$w_2$的条件概率可以计算为：

$$\hat{P}\left(w_2|w_1\right)=\frac{n\left(w_1,w_2\right)}{n\left(w_1\right)}$$

其中$n(w_1,w_2)$为语料库中以$w_1$作为第一个词，$w_2$作为第二个词的文本的数量。

n元语法

序列长度增加，计算和存储多个词共同出现的概率的复杂度会呈指数级增加。$n$元语法通过马尔可夫假设简化模型，马尔科夫假设是指一个词的出现只与前面$n$个词相关，即$n$阶马尔可夫链（Markov chain of order $n$），如果$n=1$，那么有$P(w_3\mid w_1,w_2)=P(w_3\mid w_2)$。基于$n-1$阶马尔可夫链，我们可以将语言模型改写为

$$P(w_1,w_2,\dots ,w_T)=\prod _{t=1}^{T}P(w_t\mid w_{t-(n-1)},\dots ,w_{t-1}).$$

以上也叫$n$元语法（$n$-grams），它是基于$n-1$阶马尔可夫链的概率语言模型。例如，当$n=2$时，含有4个词的文本序列的概率就可以改写为：
$$\begin{array}{rl}P\left(w_1,w_2,w_3,w_4\right)& =P\left(w_1\right)P\left(w_2|w_1\right)P\left(w_3|w_1,w_2\right)P\left(w_4|w_1,w_2,w_3\right)\\ & =P\left(w_1\right)P\left(w_2|w_1\right)P\left(w_3|w_2\right)P\left(w_4|w_3\right)\end{array}$$

当$n$分别为1、2和3时，我们将其分别称作一元语法（unigram）、二元语法（bigram）和三元语法（trigram）。例如，长度为4的序列$w_1,w_2,w_3,w_4$在一元语法、二元语法和三元语法中的概率分别为
$$\begin{array}{rl}& P\left(w_1,w_2,w_3,w_4\right)=P\left(w_1\right)P\left(w_2\right)P\left(w_3\right)P\left(w_4\right)\\ & P\left(w_1,w_2,w_3,w_4\right)=P\left(w_1\right)P\left(w_2|w_1\right)P\left(w_3|w_2\right)P\left(w_4|w_3\right)\\ & P\left(w_1,w_2,w_3,w_4\right)=P\left(w_1\right)P\left(w_2|w_1\right)P\left(w_3|w_1,w_2\right)P\left(w_4|w_2,w_3\right)\end{array}$$

当$n$较小时，$n$元语法往往并不准确。

语言模型

假设序列$w_1,w_2,\dots ,w_T$中的每个词是依次生成的，我们有

语言模型数据集

读取数据集

with open('/home/kesci/input/jaychou_lyrics4703/jaychou_lyrics.txt') as f:
    corpus_chars = f.read()
print(len(corpus_chars))
print(corpus_chars[: 40])
corpus_chars = corpus_chars.replace('\n', ' ').replace('\r', ' ')
corpus_chars = corpus_chars[: 10000]

建立字符索引

idx_to_char = list(set(corpus_chars)) # 去重，得到索引到字符的映射
char_to_idx = {char: i for i, char in enumerate(idx_to_char)} # 字符到索引的映射
vocab_size = len(char_to_idx)
print(vocab_size)

corpus_indices = [char_to_idx[char] for char in corpus_chars]  # 将每个字符转化为索引，得到一个索引的序列
sample = corpus_indices[: 20]
print('chars:', ''.join([idx_to_char[idx] for idx in sample]))
print('indices:', sample)

list(set(corpus_chars))中，set() 函数创建一个无序不重复元素集，可进行关系测试，删除重复数据，还可以计算交集、差集、并集等，list()方法用于将元组转换为列表（注：元组与列表是非常类似的，区别在于元组的元素值不能修改，元组是放在括号中，列表是放于方括号中）。
enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。 i, char in enumerate(idx_to_char)用于枚举每一个字符和每一个字符的下标。
char: i是一个字典的推导式，用于构造一个字典。
[char_to_idx[char] for char in corpus_chars]将语料中的每一个字符转化为其对应的索引得到一个索引序列，然后取出前20个索引。
[idx_to_char[idx] for idx in sample])将索引对应的字符提出，join()将提取出的字符进行拼接。
输出结果为：

1027
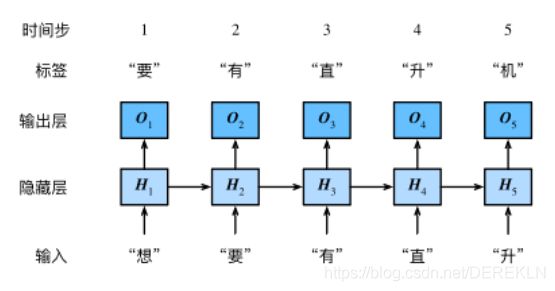
chars: 想要有直升机 想要和你飞到宇宙去 想要和
indices: [1022, 648, 1025, 366, 208, 792, 199, 1022, 648, 641, 607, 625, 26, 155, 130, 5, 199, 1022, 648, 641]

时序数据的采样

随机采样
下面的代码每次从数据里随机采样一个小批量。其中批量大小batch_size是每个小批量的样本数，num_steps是每个样本所包含的时间步数。
在随机采样中，每个样本是原始序列上任意截取的一段序列，相邻的两个随机小批量在原始序列上的位置不一定相毗邻。

import torch
import random
def data_iter_random(corpus_indices, batch_size, num_steps, device=None):
    # 减1是因为对于长度为n的序列，X最多只有包含其中的前n - 1个字符
    num_examples = (len(corpus_indices) - 1) // num_steps  # 下取整，得到不重叠情况下的样本个数
    example_indices = [i * num_steps for i in range(num_examples)]  # 每个样本的第一个字符在corpus_indices中的下标
    random.shuffle(example_indices)

    def _data(i):
        # 返回从i开始的长为num_steps的序列
        return corpus_indices[i: i + num_steps]
    if device is None:
        device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    
    for i in range(0, num_examples, batch_size):
        # 每次选出batch_size个随机样本
        batch_indices = example_indices[i: i + batch_size]  # 当前batch的各个样本的首字符的下标
        X = [_data(j) for j in batch_indices]
        Y = [_data(j + 1) for j in batch_indices]
        yield torch.tensor(X, device=device), torch.tensor(Y, device=device)

my_seq = list(range(30))
for X, Y in data_iter_random(my_seq, batch_size=2, num_steps=6):
    print('X: ', X, '\nY:', Y, '\n')

输出：

X:  tensor([[ 6,  7,  8,  9, 10, 11],
        [12, 13, 14, 15, 16, 17]]) 
Y: tensor([[ 7,  8,  9, 10, 11, 12],
        [13, 14, 15, 16, 17, 18]]) 

X:  tensor([[ 0,  1,  2,  3,  4,  5],
        [18, 19, 20, 21, 22, 23]]) 
Y: tensor([[ 1,  2,  3,  4,  5,  6],
        [19, 20, 21, 22, 23, 24]]) 

相邻采样
在相邻采样中，相邻的两个随机小批量在原始序列上的位置相毗邻。

def data_iter_consecutive(corpus_indices, batch_size, num_steps, device=None):
    if device is None:
        device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    corpus_len = len(corpus_indices) // batch_size * batch_size  # 保留下来的序列的长度
    corpus_indices = corpus_indices[: corpus_len]  # 仅保留前corpus_len个字符
    indices = torch.tensor(corpus_indices, device=device)
    indices = indices.view(batch_size, -1)  # resize成(batch_size, )
    batch_num = (indices.shape[1] - 1) // num_steps
    for i in range(batch_num):
        i = i * num_steps
        X = indices[:, i: i + num_steps]
        Y = indices[:, i + 1: i + num_steps + 1]
        yield X, Y

同样的设置下，打印相邻采样每次读取的小批量样本的输入X和标签Y。相邻的两个随机小批量在原始序列上的位置相毗邻。

for X, Y in data_iter_consecutive(my_seq, batch_size=2, num_steps=6):
    print('X: ', X, '\nY:', Y, '\n')

输出：

X:  tensor([[ 0,  1,  2,  3,  4,  5],
        [15, 16, 17, 18, 19, 20]]) 
Y: tensor([[ 1,  2,  3,  4,  5,  6],
        [16, 17, 18, 19, 20, 21]]) 

X:  tensor([[ 6,  7,  8,  9, 10, 11],
        [21, 22, 23, 24, 25, 26]]) 
Y: tensor([[ 7,  8,  9, 10, 11, 12],
        [22, 23, 24, 25, 26, 27]]) 

相邻采样与循环神经网络的结构有关系。

循环神经网络基础

one-hot向量

我们需要将字符表示成向量，这里采用one-hot向量。假设词典大小是$N$，每次字符对应一个从$0$到$N-1$的唯一的索引，则该字符的向量是一个长度为$N$的向量，若字符的索引是$i$，则该向量的第$i$个位置为$1$，其他位置为$0$。下面分别展示了索引为0和2的one-hot向量，向量长度等于词典大小。

def one_hot(x, n_class, dtype=torch.float32):
    result = torch.zeros(x.shape[0], n_class, dtype=dtype, device=x.device)  # shape: (n, n_class)
    result.scatter_(1, x.long().view(-1, 1), 1)  # result[i, x[i, 0]] = 1
    return result

在def one_hot(x, n_class, dtype=torch.float32)中，x是一个一维向量，它的每一个元素都是一个字符的索引；n_class是字典的大小。
scatter() 和 scatter_() 的作用是一样的，只不过 scatter() 不会直接修改原来的 Tensor，而 scatter_() 会。PyTorch 中，一般函数加下划线代表直接在原来的 Tensor 上修改scatter(dim, index, src) 的参数有 3 个。dim：沿着哪个维度进行索引;index：用来 scatter 的元素索引;src：用来 scatter 的源元素，可以是一个标量或一个张量。
即x是一个索引向量，x的长度对应result数组的行数，在第一个维度（即行）上索引，第i行索引到的第x[i]个元素scatter为1，得到了一个one-hot二维数组（批量数，字典长度）。

我们每次采样的小批量的形状是（批量大小, 时间步数）。由于处理小批量的过程是循环的，也就是一个时间步一个时间步的处理，相当于每一次处理小批量矩阵的一列。
下面的函数将这样的小批量变换成数个形状为（批量大小, 词典大小）的矩阵，矩阵个数等于时间步数。也就是说，时间步$t$的输入为${\mathbf{X}}_t\in {\mathbb{R}}^{n\times d}$，其中$n$为批量大小，$d$为词向量大小，即one-hot向量长度（词典大小）。

def to_onehot(X, n_class):
    return [one_hot(X[:, i], n_class) for i in range(X.shape[1])]

X = torch.arange(10).view(2, 5)
inputs = to_onehot(X, vocab_size)
print(len(inputs), inputs[0].shape)

X为小批量，n_class为字典大小。[one_hot(X[:, i], n_class) for i in range(X.shape[1])]每次取出批量矩阵的一列组成一个one-hot矩阵。

初始化模型参数

num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
# num_inputs: d
# num_hiddens: h, 隐藏单元的个数是超参数
# num_outputs: q

def get_params():
    def _one(shape):
        param = torch.zeros(shape, device=device, dtype=torch.float32)
        nn.init.normal_(param, 0, 0.01)
        return torch.nn.Parameter(param)

    # 隐藏层参数
    W_xh = _one((num_inputs, num_hiddens))
    W_hh = _one((num_hiddens, num_hiddens))
    b_h = torch.nn.Parameter(torch.zeros(num_hiddens, device=device))
    # 输出层参数
    W_hq = _one((num_hiddens, num_outputs))
    b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device))
    return (W_xh, W_hh, b_h, W_hq, b_q)

需要注意的是：隐藏单元是个超参数！

定义模型

函数rnn用循环的方式依次完成循环神经网络每个时间步的计算，也即循环神经网络的前向计算。

def rnn(inputs, state, params):
    # inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    for X in inputs:
        H = torch.tanh(torch.matmul(X, W_xh) + torch.matmul(H, W_hh) + b_h)
        Y = torch.matmul(H, W_hq) + b_q
        outputs.append(Y)
    return outputs, (H,)

# inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵：一个形状为(batch_size, vocab_size)的矩阵只代表了批量中的一列，可以理解为有n行语句，这一个矩阵只代表这个语句矩阵的一列字符，而语句是个时间序列，语句长度就是时间步长，所以输入和输出都是时间步长个矩阵，也就是inputs和outputs皆为num_steps个形状为(batch_size, vocab_size)的矩阵。
state是一个元组，其实在rnn模型中状态只有一个，也即隐藏状态。但是在后续介绍LSTM时状态不止一个，所以此处将state定义为一个元组。

函数init_rnn_state初始化隐藏变量，这里的返回值是一个元组。

def init_rnn_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )

此函数最终返回的也是一个元组，原因同上。

裁剪梯度

循环神经网络的梯度是通过后向传播得到的，结果是一个幂的形式，幂的指数是时间步数，因此循环神经网络中较容易出现梯度衰减或梯度爆炸，这会导致网络几乎无法训练。裁剪梯度（clip gradient）是一种应对梯度爆炸的方法。假设我们把所有模型参数的梯度拼接成一个向量 $\mathbf{g}$，并设裁剪的阈值是$\theta$。裁剪后的梯度

$$\min \left(\frac{\theta }{\Vert \mathbf{g}\Vert },1\right)\mathbf{g}$$

的$L_2$范数不超过$\theta$。

def grad_clipping(params, theta, device):
    norm = torch.tensor([0.0], device=device)
    for param in params:
        norm += (param.grad.data ** 2).sum()
    norm = norm.sqrt().item()
    if norm > theta:
        for param in params:
            param.grad.data *= (theta / norm)

定义预测函数

以下函数基于前缀prefix（含有数个字符的字符串）来预测接下来的num_chars个字符。这个函数稍显复杂，其中我们将循环神经单元rnn设置成了函数参数，这样在后面小节介绍其他循环神经网络时能重复使用这个函数。

def predict_rnn(prefix, num_chars, rnn, params, init_rnn_state,
                num_hiddens, vocab_size, device, idx_to_char, char_to_idx):
    state = init_rnn_state(1, num_hiddens, device)
    output = [char_to_idx[prefix[0]]]   # output记录prefix加上预测的num_chars个字符
    for t in range(num_chars + len(prefix) - 1):
        # 将上一时间步的输出作为当前时间步的输入
        X = to_onehot(torch.tensor([[output[-1]]], device=device), vocab_size)
        # 计算输出和更新隐藏状态
        (Y, state) = rnn(X, state, params)
        # 下一个时间步的输入是prefix里的字符或者当前的最佳预测字符
        if t < len(prefix) - 1:
            output.append(char_to_idx[prefix[t + 1]])
        else:
            output.append(Y[0].argmax(dim=1).item())
    return ''.join([idx_to_char[i] for i in output])

给定模型参数和前缀prefix来预测接下来的字符，预测思路：
首先利用模型处理前缀得到一个隐藏状态H，隐藏状态H中就记录了关于prefix的训练信息。由于模型在处理prefix的最后一个字符的时候已经对下一个字符进行了预测，因此这个预测可以作为下一个时刻的输入。重复这个过程知道模型预测出了num_chars个字符为止。

困惑度

我们通常使用困惑度（perplexity）来评价语言模型的好坏。回忆一下“softmax回归”一节中交叉熵损失函数的定义。困惑度是对交叉熵损失函数做指数运算后得到的值。特别地，

• 最佳情况下，模型总是把标签类别的概率预测为1，此时困惑度为1；
• 最坏情况下，模型总是把标签类别的概率预测为0，此时困惑度为正无穷；
• 基线情况下，模型总是预测所有类别的概率都相同，此时困惑度为类别个数。

显然，任何一个有效模型的困惑度必须小于类别个数。在本例中，困惑度必须小于词典大小vocab_size。

定义模型训练函数

跟之前章节的模型训练函数相比，这里的模型训练函数有以下几点不同：

1. 使用困惑度评价模型。
2. 在迭代模型参数前裁剪梯度。
3. 对时序数据采用不同采样方法将导致隐藏状态初始化的不同。

def train_and_predict_rnn(rnn, get_params, init_rnn_state, num_hiddens,
                          vocab_size, device, corpus_indices, idx_to_char,
                          char_to_idx, is_random_iter, num_epochs, num_steps,
                          lr, clipping_theta, batch_size, pred_period,
                          pred_len, prefixes):
    if is_random_iter:
        data_iter_fn = d2l.data_iter_random
    else:
        data_iter_fn = d2l.data_iter_consecutive
    params = get_params()
    loss = nn.CrossEntropyLoss()

is_random_iter参数用来判断使用哪种采样方法，随机采样or相邻采样。相邻采样的特点是两个相邻的batch在训练数据上是连续的，所以如果采用相邻采样，只需在每个epoch开始的时候初始化隐藏状态。但是这也带来一个问题，就是在同一个epoch中，随着batch的增大，模型的损失函数关于隐藏变量的梯度传播得更远，计算开销也更大。所以为了减小计算开销，一般是在每个batch开始的时候把隐藏状态从计算图当中分离出来。

    for epoch in range(num_epochs):
        if not is_random_iter:  # 如使用相邻采样，在epoch开始时初始化隐藏状态
            state = init_rnn_state(batch_size, num_hiddens, device)
        l_sum, n, start = 0.0, 0, time.time()
        data_iter = data_iter_fn(corpus_indices, batch_size, num_steps, device)
        for X, Y in data_iter:
            if is_random_iter:  # 如使用随机采样，在每个小批量更新前初始化隐藏状态
                state = init_rnn_state(batch_size, num_hiddens, device)
            else:  # 否则需要使用detach函数从计算图分离隐藏状态
                for s in state:
                    s.detach_()
            # inputs是num_steps个形状为(batch_size, vocab_size)的矩阵
            inputs = to_onehot(X, vocab_size)
            # outputs有num_steps个形状为(batch_size, vocab_size)的矩阵
            (outputs, state) = rnn(inputs, state, params)
            # 拼接之后形状为(num_steps * batch_size, vocab_size)
            outputs = torch.cat(outputs, dim=0)
            # Y的形状是(batch_size, num_steps)，转置后再变成形状为
            # (num_steps * batch_size,)的向量，这样跟输出的行一一对应
            y = torch.flatten(Y.T)
            # 使用交叉熵损失计算平均分类误差
            l = loss(outputs, y.long())
            
            # 梯度清0
            if params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            l.backward()
            grad_clipping(params, clipping_theta, device)  # 裁剪梯度
            d2l.sgd(params, lr, 1)  # 因为误差已经取过均值，梯度不用再做平均
            l_sum += l.item() * y.shape[0]
            n += y.shape[0]

        if (epoch + 1) % pred_period == 0:
            print('epoch %d, perplexity %f, time %.2f sec' % (
                epoch + 1, math.exp(l_sum / n), time.time() - start))
            for prefix in prefixes:
                print(' -', predict_rnn(prefix, pred_len, rnn, params, init_rnn_state,
                    num_hiddens, vocab_size, device, idx_to_char, char_to_idx))

循环神经网络的简洁实现

定义模型

我们使用Pytorch中的nn.RNN来构造循环神经网络。在本节中，我们主要关注nn.RNN的以下几个构造函数参数：

• input_size - The number of expected features in the input x
• hidden_size – The number of features in the hidden state h
• nonlinearity – The non-linearity to use. Can be either ‘tanh’ or ‘relu’. Default: ‘tanh’
• batch_first – If True, then the input and output tensors are provided as (batch_size, num_steps, input_size). Default: False

这里的batch_first决定了输入的形状，我们使用默认的参数False，对应的输入形状是 (num_steps, batch_size, input_size)。

forward函数的参数为：

• input of shape (num_steps, batch_size, input_size): tensor containing the features of the input sequence.
• h_0 of shape (num_layers * num_directions, batch_size, hidden_size): tensor containing the initial hidden state for each element in the batch. Defaults to zero if not provided. If the RNN is bidirectional, num_directions should be 2, else it should be 1.
  若没有对h_0进行设置，则默认为0。

forward函数的返回值是：

• output of shape (num_steps, batch_size, num_directions * hidden_size): tensor containing the output features (h_t) from the last layer of the RNN, for each t.
• h_n of shape (num_layers * num_directions, batch_size, hidden_size): tensor containing the hidden state for t = num_steps.

现在我们构造一个nn.RNN实例，并用一个简单的例子来看一下输出的形状。

rnn_layer = nn.RNN(input_size=vocab_size, hidden_size=num_hiddens)
num_steps, batch_size = 35, 2
X = torch.rand(num_steps, batch_size, vocab_size)
state = None
Y, state_new = rnn_layer(X, state)
print(Y.shape, state_new.shape)

torch.Size([35, 2, 256]) torch.Size([1, 2, 256])

定义一个完整的基于循环神经网路的语言模型。

class RNNModel(nn.Module):
    def __init__(self, rnn_layer, vocab_size):
        super(RNNModel, self).__init__()
        self.rnn = rnn_layer
        self.hidden_size = rnn_layer.hidden_size * (2 if rnn_layer.bidirectional else 1) 
        self.vocab_size = vocab_size
        self.dense = nn.Linear(self.hidden_size, vocab_size)

    def forward(self, inputs, state):
        # inputs.shape: (batch_size, num_steps)
        X = to_onehot(inputs, vocab_size)
        X = torch.stack(X)  # X.shape: (num_steps, batch_size, vocab_size)
        hiddens, state = self.rnn(X, state)
        hiddens = hiddens.view(-1, hiddens.shape[-1])  # hiddens.shape: (num_steps * batch_size, hidden_size)
        output = self.dense(hiddens)
        return output, state

其中X = torch.stack(X) # X.shape: (num_steps, batch_size, vocab_size)用于将每个小批量的数据X堆叠起来，即按照时间维度扩展。
类似的，我们需要实现一个预测函数，与前面的区别在于前向计算和初始化隐藏状态。

def predict_rnn_pytorch(prefix, num_chars, model, vocab_size, device, idx_to_char,
                      char_to_idx):
    state = None
    output = [char_to_idx[prefix[0]]]  # output记录prefix加上预测的num_chars个字符
    for t in range(num_chars + len(prefix) - 1):
        X = torch.tensor([output[-1]], device=device).view(1, 1)
        (Y, state) = model(X, state)  # 前向计算不需要传入模型参数
        if t < len(prefix) - 1:
            output.append(char_to_idx[prefix[t + 1]])
        else:
            output.append(Y.argmax(dim=1).item())
    return ''.join([idx_to_char[i] for i in output])

接下来实现训练函数，这里只使用了相邻采样。

def train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
                                corpus_indices, idx_to_char, char_to_idx,
                                num_epochs, num_steps, lr, clipping_theta,
                                batch_size, pred_period, pred_len, prefixes):
    loss = nn.CrossEntropyLoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)
    model.to(device)
    for epoch in range(num_epochs):
        l_sum, n, start = 0.0, 0, time.time()
        data_iter = d2l.data_iter_consecutive(corpus_indices, batch_size, num_steps, device) # 相邻采样
        state = None
        for X, Y in data_iter:
            if state is not None:
                # 使用detach函数从计算图分离隐藏状态
                if isinstance (state, tuple): # LSTM, state:(h, c)  
                    state[0].detach_()
                    state[1].detach_()
                else: 
                    state.detach_()
            (output, state) = model(X, state) # output.shape: (num_steps * batch_size, vocab_size)
            y = torch.flatten(Y.T)
            l = loss(output, y.long())
            
            optimizer.zero_grad()
            l.backward()
            grad_clipping(model.parameters(), clipping_theta, device)
            optimizer.step()
            l_sum += l.item() * y.shape[0]
            n += y.shape[0]
        

        if (epoch + 1) % pred_period == 0:
            print('epoch %d, perplexity %f, time %.2f sec' % (
                epoch + 1, math.exp(l_sum / n), time.time() - start))
            for prefix in prefixes:
                print(' -', predict_rnn_pytorch(
                    prefix, pred_len, model, vocab_size, device, idx_to_char,
                    char_to_idx))

习题知识点摘录

• 批量训练的过程中，参数是以批为单位更新的，每个批次内模型的参数都是一样的。
• 循环神经网络通过不断循环使用同样一组参数来应对不同长度的序列，故网络的参数数量与输入序列长度无关。
• 隐藏状态的值不能并行计算，后一个时间步的隐藏状态是基于此前的所有隐藏状态获得的。
• 一个随机分类模型（基线模型）的困惑度等于分类问题的类别个数，有效模型的困惑度应小于类别个数。
• 采用的采样方法不同会导致隐藏状态初始化方式发生变化，采用相邻采样仅在每个训练周期开始的时候初始化隐藏状态是因为相邻的两个批量在原始数据上是连续的，随机采样中每个样本只包含局部的时间序列信息，因为样本不完整所以每个批量需要重新初始化隐藏状态。