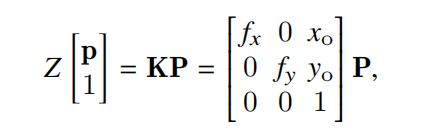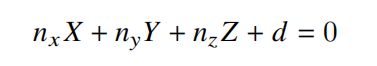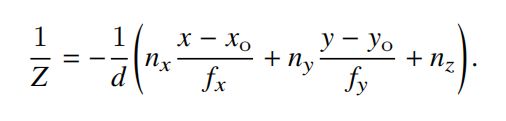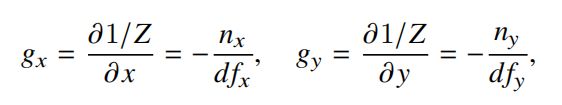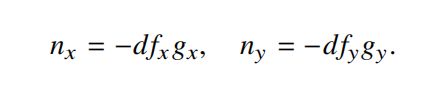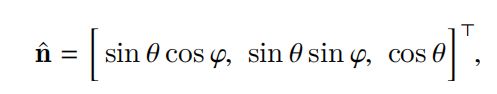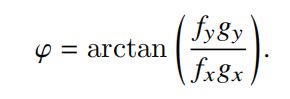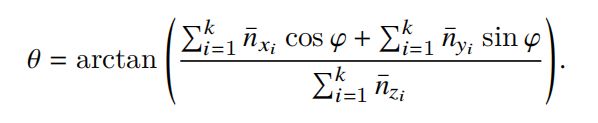道路检测 | SNE-RoadSeg论文阅读
道路检测 | SNE-RoadSeg: Incorporating Surface Normal Information into Semantic Segmentation for Accurate Freespace Detection论文阅读
论文地址:https://arxiv.org/abs/2008.11351
开源代码:https://github.com/hlwang1124/SNE-RoadSeg
论文作者及研究团队概述:
Rui (Ranger) Fan:Postdoc Fellow at UC San Diego
Hengli Wang:Ph.D. candidate at HKUST
Peide Cai:Ph.D. candidate at HKUST
Ming Liu:Associate Professor at HKUST
文章目录
- 道路检测 | SNE-RoadSeg: Incorporating Surface Normal Information into Semantic Segmentation for Accurate Freespace Detection论文阅读
-
-
- 1.整体框架概述
- 2.SNE模块
- 3.实验
-
- 3.1评估SNE
- 3.2评估SNE-RoadSeg
- 4.消融实验
- 5.总结
-
1.整体框架概述
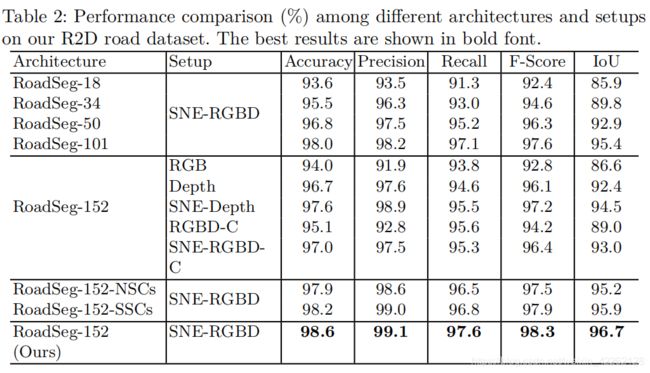
在这篇论文中,首先介绍了一个名为表面法线估计器( surface normal estimator ,SNE)的新型模块,该模块可以从密集的深度/视差图像中高精度和高效率地推断出表面法线信息。这个思想基于将所检测的空间假设为一个地面平面,在这个平面上,各点具有相似的表面法线。 此外,提出了一种称为RoadSeg的数据融合CNN架构,该架构可以从RGB图像和推断出的表面法线信息中提取并融合特征,以进行准确的自由空间检测。同时,出于研究目的,作者发布了在不同光照和天气条件下收集的大规模合成自由空间检测数据集,名为Ready-to-Drive(R2D)道路数据集。
本文提出的SNE-RoadSeg整体框架如下图所示,它由SNE模块,一个RGB编码器,一个表面法线编码器和一个具有紧密连接的跳跃连接的解码器组成。 首先采用RGB编码器和表面法线编码器分别从RGB图像和推断的表面法线信息中提取特征图,提取的RGB和表面法线特征图通过逐元素求和进行分层融合。然后通过密集连接的跳跃连接在融合器中再次融合特征图,以恢复特征图的分辨率。在RoadSeg的末尾,使用一个Sigmoid层来生成用于语义驾驶场景分割的概率图。
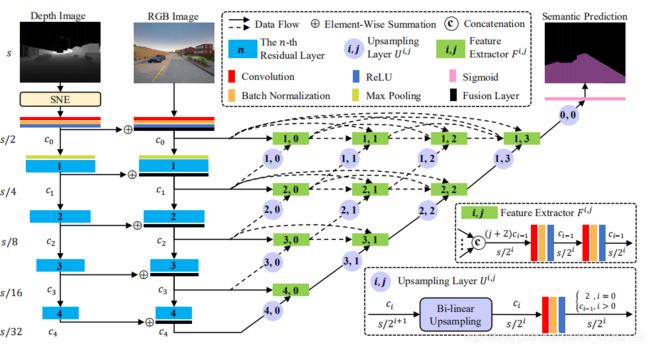
本文使用ResNet作为RGB和表面法线编码器的主干网络,它们的结构彼此相同。具体来说,初始块由卷积层,批处理归一化层和ReLU激活函数层组成。然后,依次采用最大池化层和四个残差层,以逐渐降低分辨率并增加特征图通道的数量。ResNet具有五种体系结构:ResNet-18,ResNet-34,ResNet-50,ResNet-101和ResNet-152。RoadSeg对于ResNet-18和ResNet-34,c0-c4的通道数分别为64、64、128、256和512,对于ResNet-50,ResNet-101和ResNet-152,c0-c4的通道数分别为64、256、512、1024和2048。
解码器由两类不同的模块组成:特征提取器和上采样层,这两类模块密集连接,实现灵活的特征融合。采用特征提取器从融合后的特征图中提取特征,并保证特征图分辨率不变。
2.SNE模块
这部分是这篇论文的核心部分,提出了一种利用深度图估计表面法线信息的方法。整体思路是对于有一幅深度图,可以联系CCS坐标获得每个pixel的三维信息,在此基础上利用Sobel算子或者其他梯度算子计算水平和垂直梯度以此获得法线信息的x,y方向分量。既然是是深度图,那就可以用一个邻域来估计z方向的法向量分量,这里采用K-D tree选出8个近邻点来求邻域中像素的深度差得到法向量。
下面具体分析这一部分:
对于一幅深度图像来说,其包含的信息就是空间中每个点的深度信息,在CCS坐标中可以用照相机内矩阵将二维的点的坐标与三维点的坐标相关联。即:
其中K为照相机内矩阵,x0、y0为图像中心点,fx和fy为水平焦距和垂直焦距。
求解法向量最简单的方法是通过三维点的坐标去拟合一个空间平面方程,即:
这样X,Y,Z的系数就是法向量的三个分量。结合上边的两个式子可以求出1/Z即逆深度图:
用上述的逆深度图式子分别对x,y求微分,即通过卷积求逆深度图的水平和垂直分量,这样就可以得到想要的点的法线信息的x,y分量。
用选出的所求点的k个近邻点的坐标值的偏移量代入到逆深度图的式子中可以得到k个z方向的法线分量,那么此时对于某一个点来说,估计出的法线信息就有如下k个,即:
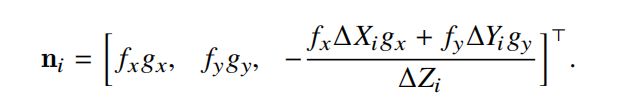
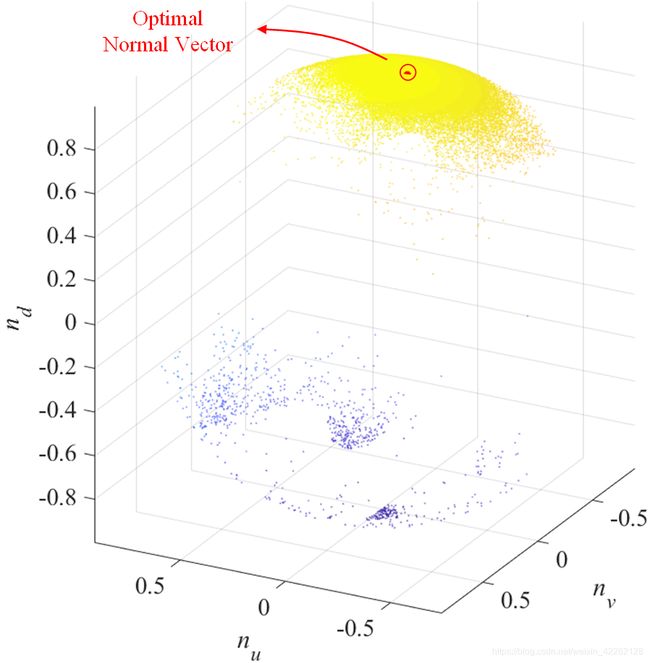
此时对上述的法线信息做一个归一化,得到k个单位向量,这些单位向量的起点是一致的,那么就可以认为这些向量的终点落在一个以起点为圆心半径为1的球体上,而我们要求解的最优法向量一定是坐在这些k个向量分布最密集的地方,如下图所示:
基于这个理论,将欧式坐标下的法线信息转化为球坐标,即:
式子中的θ表示倾角,φ表示方位,求解最优的法向量通过最小化动量的方式得到最终的法线信息结果。
整个SNE模块的代码如下所示:
import torch
import torch.nn as nn
import torch.nn.functional as F
class SNE(nn.Module):
"""Our SNE takes depth and camera intrinsic parameters as input,
and outputs normal estimations.
"""
def __init__(self):
super(SNE, self).__init__()
def forward(self, depth, camParam):
h,w = depth.size()
v_map, u_map = torch.meshgrid(torch.arange(h), torch.arange(w))
v_map = v_map.type(torch.float32)
u_map = u_map.type(torch.float32)
Z = depth # h, w
Y = Z.mul((v_map - camParam[1,2])) / camParam[0,0] # h, w
X = Z.mul((u_map - camParam[0,2])) / camParam[0,0] # h, w
Z[Y <= 0] = 0
Y[Y <= 0] = 0
Z[torch.isnan(Z)] = 0
D = torch.div(torch.ones(h, w), Z) # h, w
Gx = torch.tensor([[0,0,0],[-1,0,1],[0,0,0]], dtype=torch.float32)
Gy = torch.tensor([[0,-1,0],[0,0,0],[0,1,0]], dtype=torch.float32)
Gu = F.conv2d(D.view(1,1,h,w), Gx.view(1,1,3,3), padding=1)
Gv = F.conv2d(D.view(1,1,h,w), Gy.view(1,1,3,3), padding=1)
nx_t = Gu * camParam[0,0] # 1, 1, h, w
ny_t = Gv * camParam[1,1] # 1, 1, h, w
phi = torch.atan(torch.div(ny_t, nx_t)) + torch.ones([1,1,h,w])*3.141592657
a = torch.cos(phi)
b = torch.sin(phi)
diffKernelArray = torch.tensor([[-1, 0, 0, 0, 1, 0, 0, 0, 0],
[ 0,-1, 0, 0, 1, 0, 0, 0, 0],
[ 0, 0,-1, 0, 1, 0, 0, 0, 0],
[ 0, 0, 0,-1, 1, 0, 0, 0, 0],
[ 0, 0, 0, 0, 1,-1, 0, 0, 0],
[ 0, 0, 0, 0, 1, 0,-1, 0, 0],
[ 0, 0, 0, 0, 1, 0, 0,-1, 0],
[ 0, 0, 0, 0, 1, 0, 0, 0,-1]], dtype=torch.float32)
sum_nx = torch.zeros((1,1,h,w), dtype=torch.float32)
sum_ny = torch.zeros((1,1,h,w), dtype=torch.float32)
sum_nz = torch.zeros((1,1,h,w), dtype=torch.float32)
for i in range(8):
diffKernel = diffKernelArray[i].view(1,1,3,3)
X_d = F.conv2d(X.view(1,1,h,w), diffKernel, padding=1)
Y_d = F.conv2d(Y.view(1,1,h,w), diffKernel, padding=1)
Z_d = F.conv2d(Z.view(1,1,h,w), diffKernel, padding=1)
nz_i = torch.div((torch.mul(nx_t, X_d) + torch.mul(ny_t, Y_d)), Z_d)
norm = torch.sqrt(torch.mul(nx_t, nx_t) + torch.mul(ny_t, ny_t) + torch.mul(nz_i, nz_i))
nx_t_i = torch.div(nx_t, norm)
ny_t_i = torch.div(ny_t, norm)
nz_t_i = torch.div(nz_i, norm)
nx_t_i[torch.isnan(nx_t_i)] = 0
ny_t_i[torch.isnan(ny_t_i)] = 0
nz_t_i[torch.isnan(nz_t_i)] = 0
sum_nx = sum_nx + nx_t_i
sum_ny = sum_ny + ny_t_i
sum_nz = sum_nz + nz_t_i
theta = -torch.atan(torch.div((torch.mul(sum_nx, a) + torch.mul(sum_ny, b)), sum_nz))
nx = torch.mul(torch.sin(theta), torch.cos(phi))
ny = torch.mul(torch.sin(theta), torch.sin(phi))
nz = torch.cos(theta)
nx[torch.isnan(nz)] = 0
ny[torch.isnan(nz)] = 0
nz[torch.isnan(nz)] = -1
sign = torch.ones((1,1,h,w), dtype=torch.float32)
sign[ny > 0] = -1
nx = torch.mul(nx, sign).squeeze(dim=0)
ny = torch.mul(ny, sign).squeeze(dim=0)
nz = torch.mul(nz, sign).squeeze(dim=0)
return torch.cat([nx, ny, nz], dim=0)
3.实验
3.1评估SNE
用平均角度误差(average angular error)来量化SNE模块的准确性,通过与已有的法线信息估计方法SRI和LINE-MOD对比发现SNE的准确性在室内和室外场景下均优于这两种已有方法。定性和定量的分析如下图所示:
3.2评估SNE-RoadSeg
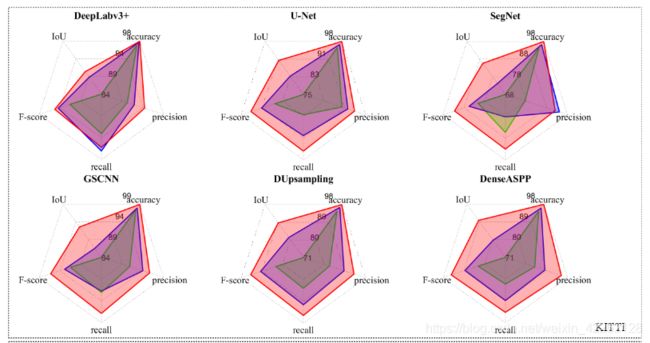
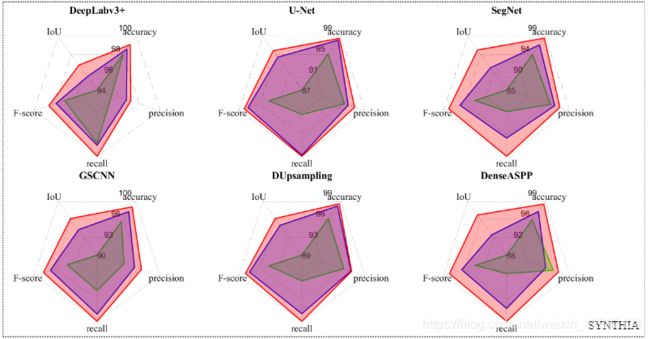
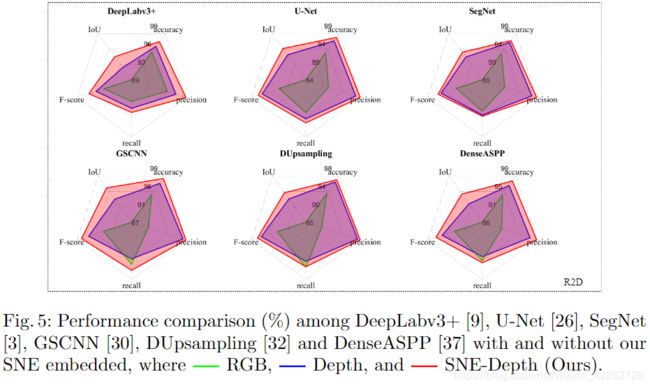
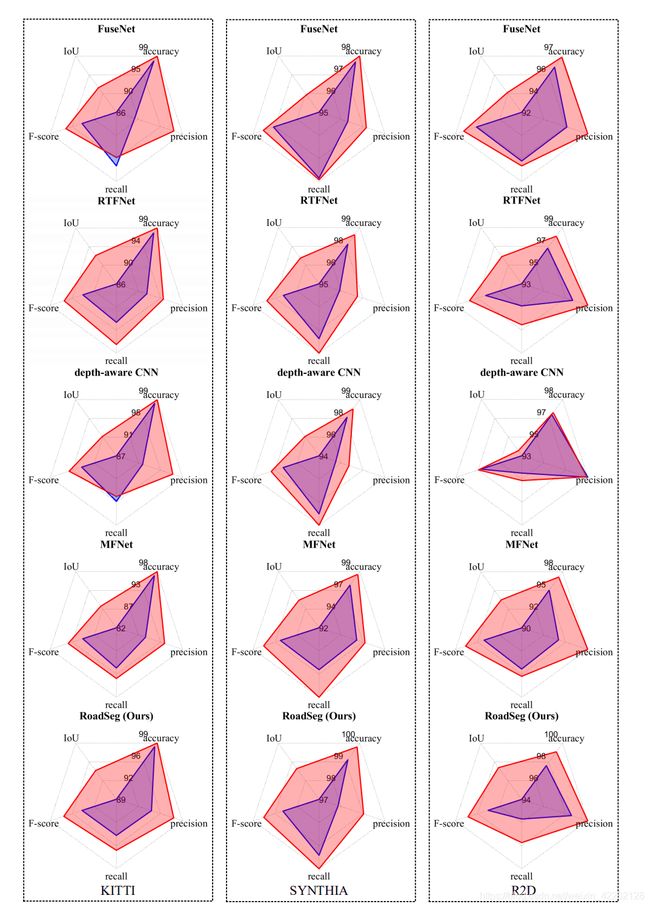
上面的两幅图像是对比了SYNTHIA道路数据集和R2D数据集后得到的结果示例。其中(i)RGB,(ii)Depth,(iii)SNE-Depth,(iv)RGBD,(v)SNE-RGBD;(1)Deep Labv3+,(2)U-Net,(3)SegNet,(4)GSCNN,(5)DUpsampling,(6)DenseASPP,(7)FuseNet,(8)RTFNet,(9)Depth-aware CNN,(10)MFNet和(11)RoadSeg。通过实验发现,CNN架构以RGB图像作为输入很大程度上受到光照条件的制约,并且对于嵌入SNE模块和不嵌入SNE模块最终的效果也有明显的差别。
从上边几幅图可以看出,嵌入SNE的方法对于单模态CNN在IoU上提升2-12%,F-score提升1-7%;对于数据融合的CNN架构在IoU上提升1-7%,在F-score提升1-4%。确确实实证明了SNE模块使得道路区域高度可分。而且也可以看到,SNE-RoadSeg架构也优于上述其他CNN架构,在IoU上提升1.4-14.7%,F-score提升0.7-8.8%,证明了使用密集连接的跳跃连接可以帮助实现灵活的特征融合并且平滑梯度流可以产生道路检测的精确结果。
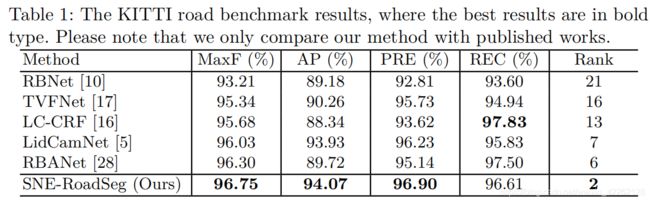
由上图和表格可以看出,SNE-RoadSeg在MaxF,AP,PRE上都达到了最高的精度,总体在KITTI上排名第二。
4.消融实验
5.总结
这篇论文的主要贡献包括:1、提出了SNE一种表面法线估计方法,可以从深度/视差图中高精度、高效率的推断表面法线信息;2、提出了一个名为SNE-RoadSeg的数据融合CNN架构,通过融合从RGB以及法线图像提取的特征中高精度的实现道路检测;3、发布了一个用于自动驾驶道路检测的合成数据集R2D。为了证明SNE模块的灵活性与有效性将其嵌入到十个最先进的CNN架构中评估了它们在道路检测中的性能,证明了其可以提高这些CNN的性能同时也证明了SNE-RoadSeg在道路检测上的性能更优。