图像处理: OpenCV编程详解(C++) 【持续更新中】

原创不易，请勿抄袭
作者联系方式 : QQ:993678929

---

一. 开发环境配置

Visual Studio 2019 + opencv
这里仅记录配置过程中可能遇到的问题

1. 由于找不到 opencv_world450.dll，无法继续执行代码。重新安装程序可能会解决此问题。

找到 C:\opencv\build\x64\vc15\bin 文件夹，将其中的opencv_videoio_ffmpeg450_64.dll opencv_videoio_msmf450_64.dll opencv_world450.dll 三个dll文件复制到C:\Windows\System32目录下（如果VS需要使用debug模式编译运行则把带d的dll也一同复制）

2. 在VS项目属性中添加包含目录和库目录以及添加链接器输入的附加依赖项时注意选择配置和平台
   
   Debug和Release分别对应带d和不带d的lib文件（opencv_world450d.lib和opencv_world450.lib ）
   而x64和x86则应该根据你所安装的opencv版本对应的平台来选择

---

二. 图像的数字化

1.构造Mat类

#include 

using namespace cv;

int main()
{
	
	Mat m1 = Mat(4, 2, CV_64FC(1));     //构造一个4列2行（宽4 高2）的double类型矩阵
	Mat m2 = Mat(Size(4,2),CV_64FC(1));  //这种写法也可以，同样的效果
	Mat m3 = (Mat_<int>(4, 2) << 1, 2, 3, 4, 5, 6，7，8);  //快速构造小型单通道矩阵（int类型）并初始化。
	Mat m4; 
	m4.create(4,2,CV_64FC1);   //调用Mat的成员函数create构造单通道矩阵
	Mat m_one = Mat::ones(4, 2, CV_32FC1);  //构造4列 2行的单通道1矩阵
	Mat m_zero = Mat::zeros(4, 2, CV_32FC1);  //构造4列 2行的单通道1矩阵
	return 0;
}

构造m1时传入的三个参数，4表示矩阵的列数（宽度），2表示矩阵的行数（高度）
而在CV_64FC(1)中:
64F表示将要构造的Mat对象中每一个数值占用64bit且是浮点数，即占8字节的double类型，32F就是占4字节（32bit）的float类型
C(n)表示通道数，当n=1时，即构造单通道矩阵（二维矩阵）,当n>1时构造的是n通道矩阵（三维矩阵），可理解为由n个二维矩阵叠加形成的三维矩阵
后面几种初始化方式里CV_64FC1等末尾的1也是表示通道数

2. 常用属性/函数

m为一个Mat对象。
m.rows m的行数
m.cols m的列数
m.dims m的维数，单通道是二维矩阵，多通道是三维矩阵

• m.channels() m的通道数
• m.total() m的面积（行数乘以列数），与通道数无关
• m.at(r,c) 第r行，第c列的值，从0开始（即矩阵的第一个数是第0行第0列）。<>中的数据类型应与m中存储的数据类型一致。
  下面的程序构造了一个2行4列的矩阵并遍历输出它的每个元素

#include 
#include 

using namespace cv;
using namespace std;

int main()
{
	Mat m = (Mat_<float>(2, 4) << 1, 2, 3, 4, 5, 6,7,8);
	for (int r = 0; r < m.rows; r++)
	{
		for (int c = 0; c < m.cols; c++)
			cout << m.at<float>(r, c) << ' ';
		cout << endl;
	}
	return 0;
}

输出：

1 2 3 4
5 6 7 8

• m.isContinuous() 若为真则m中行与行是连续存储
• m.ptr(r) 指向第r行首地址的指针。下面的代码演示了通过ptr函数遍历Mat,输出和上面的完全相同

for (int r = 0; r < m.rows; r++)
	{
		const float* ptr = m.ptr<float>(r);
		for (int c = 0; c < m.cols; c++)
			cout << ptr[c] << " ";
		cout << endl;
	}

• m.row(r) 返回m的第r行，返回值仍是一个单通道的Mat

• m.col(c) 返回m的第c列，返回值仍是一个单通道的Mat

• split(mm,planes) 分离多通道矩阵mm为多个单通道矩阵并保存在动态数组planes中，其中planes的声明为

	std::vector<Mat> planes;

（注：需要#include ）

• merge(planes,n,mm) 将n个单通道Mat合并为一个多通道Mat，其中mm为多通道Mat，planes为Mat数组，n为planes数组的长度，即有几个单通道Mat
  以三通道矩阵为例，plane定义如下:

Mat planes[] = {plane0,plane1,plane2};

也可以使用merge函数的重载:
merge(planes,mm) 其中planes为std::vector动态数组，mm为Mat类对象

对矩阵的某个部分进行处理时经常需要获取其连续行或者连续列，或者说矩阵的子矩阵:

• m.rowRange(Range(i,j)) 获取m的第i到第j-1行，返回值为一个Mat
  其中Range(i,j) 表示连续整数序列 [ i , j ) 注意这是一个左闭右开区间，类似于python中的range
  示例:

Mat r_range=m.rowRange(Range(1,4));  //获取m的第1~第3行 

也可以直接使用它的重载，不写Range:

Mat r_range=m.rowRange(1,4);  //效果同上

那么类似的也有获取Mat连续列的函数:

• m.colRange(Range(i,j)) 用法同上，不再赘述

需要注意的是，上面两个函数返回的子矩阵是对原矩阵的引用。即如果修改子矩阵r_range，原矩阵相应地也会被改变。如果不想改变原矩阵中的值，即想要获取一个拷贝的子矩阵，可以使用clone函数：

• m.clone() 返回m的拷贝
  即：

Mat r_range=m.rowRange(1,4).clone();   //获取m的第1~3行构成的矩阵

这样获得的r_range和原矩阵m就没有任何联系了

---

3. 运算

• 加减乘

OpenCV重载了Mat类矩阵加 减 乘法的运算符，因此，矩阵的加 减 乘 只需要：
Mat dst = src1 + src2; src1和src2必须为行列数相同的矩阵否则会引发异常
下面的例子演示了两个uchar类型的矩阵相加之后输出结果
uchar取值范围为0~255，是图像处理中常用的数据类型

	Mat src1 = (Mat_<uchar>(2, 3) << 243, 123, 32, 23, 2, 65);
	Mat src2 = (Mat_<uchar>(2, 3) << 100, 53, 72, 238, 26, 64);
	Mat dst = a + b;
	for (int i = 0; i < dst.rows; i++)
	{
		for (int j = 0; j < dst.cols; j++)
			printf("%d ",dst.at<uchar>(i, j));
		cout << endl;
	}

运行结果：

255 176 104
255 28 129

当相加结果超过255时会截断成255
当我们把上面第三行的+号改成-号之后运行结果如下：

143 70 0
0 0 1

相减结果小于0时截断成0
注意矩阵的乘法只能用于float和double类型的Mat对象，且必须满足矩阵乘除法的数学规定。否则会在运行时产生异常

• 点乘 点除
  矩阵的的点乘可以用成员函数mul
  Mat dst=src1.mul(src2)
  即用src1的每一个元素乘以src2对应位置上的元素。src1和src2的数据类型必须一致，没有矩阵乘法那样的类型限制

点除直接使用/运算符，没有矩阵乘法那样的类型限制

• 指数，对数
  注意这里的指数和对数运算是对矩阵中每一个元素进行的。
  pow(src,k,dst) 指数运算，将src的k次方保存在dst中，k必须为整数。
  示例:

	Mat src = (Mat_<uchar>(2, 2) << 1, 3, 4, 16);
	Mat dst;
	pow(src, 2, dst);
	cout << dst << endl;

输出：(因为是uchar类型，所以大于255的截断成255了，这是本文最后一次解释）

[  1,   9;
  16, 255]

当k不为整数时，Mat的类型需为float或double，否则会产生运行时异常

4. 读取图像并转换为Mat（图像数字化）

imread函数的定义如下
Mat imread( const String& filename, int flags = IMREAD_COLOR );
该函数以指定的模式（flag）读取图像文件，定义在头文件中
flags允许的值：
IMREAD_COLOR 彩色图像
IMREAD_GRAYSCALE 灰度图像（如果filename指定的是彩色图像，则会转换成灰度图像显示）
IMREAD_ANYCOLOR 任意图像（自适应）
示例：

	Mat img = imread("1.jpg",IMREAD_ANYCOLOR);  //读取同目录下的1.jpg文件
	if (!img.empty())
	{
		string title = "Picture";
		namedWindow(title, WINDOW_AUTOSIZE); //新建一个标题为title的窗口，根据内容自适应大小
		imshow(title,img);   //将img显示在标题为title的窗口中
		waitKey(0);  //等待任意按键关闭图像，如果不加这个则窗口会一闪而过
	}

运行效果：（PS : 这是我的QQ头像）

• 单通道Mat灰度图像
  我们打开windows自带的画图软件，先把画布的大小调整为20x20像素
  然后我们来画一个简单的笑脸：
  
  保存为smile.bmp
  然后我们来读取图像并打印Mat的值：

#include 
#include 
#include 
using namespace cv;
using namespace std;
int main()
{
	Mat img = imread("smile.bmp",IMREAD_ANYCOLOR);
	if (!img.empty())
	{
		string title = "Picture";
		namedWindow(title, WINDOW_AUTOSIZE);
		imshow(title,img);
		waitKey(0);
		cout << img << endl;
	}
	return 0;
}	

我们画的图像显示出来的了，很小，因为我们这里没有缩放，20*20=400个像素在如今1080P的屏幕上就是很小一块，如果你用的是2K或者更高分辨率的屏幕它会小得更离谱
随便按一个键：

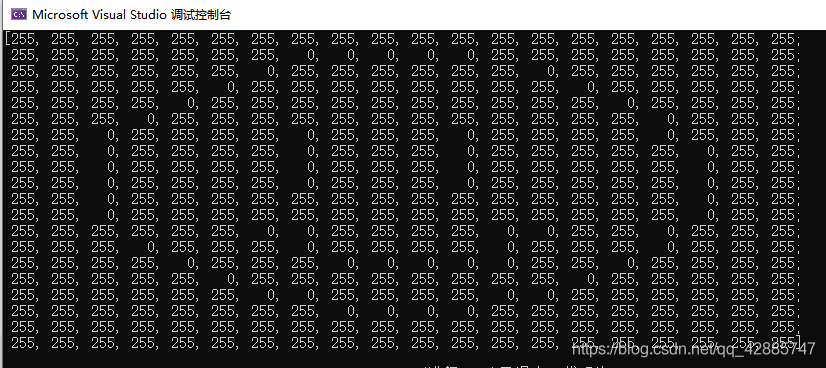
看，我们得到的正是一个20*20的矩阵，每个数字代表着对应的像素点的颜色，255是纯白色，0是纯黑色，在这里255和0也勾勒出了一个笑脸的模样。这就是图像数字化的魅力。
我们可以把img里的255全改成一个小一点的灰度值（灰度值越小颜色越深）再显示：

#include 
#include 
#include 
using namespace cv;
using namespace std;
int main()
{
	Mat img = imread("smile.bmp",IMREAD_ANYCOLOR);
	string title = "Picture";
    namedWindow(title, WINDOW_NORMAL);  //WINDOW_NORMAL模式下的窗口可以被用户改变大小
	for (int r = 0; r < img.rows; r++)
	{
		for (int c = 0; c < img.cols; c++)
			if (img.at<uchar>(r, c) == 255)
				img.at<uchar>(r, c) = 200;
		
	}
	cout << img << endl;
	imshow(title, img);
	waitKey(0);
	return 0;
}	

看，背景变灰了
我们再试试颜色反转：
（修改上面的for循环）

for (int r = 0; r < img.rows; r++)
	{
		for (int c = 0; c < img.cols; c++)
			img.at<uchar>(r, c) = 255 - img.at<uchar>(r, c);
	}

• 三通道（R,G,B）Mat 彩色图像
  如果读取的图像是彩色图像则得到的Mat是一个三通道矩阵，我们应该先分离三个通道，分别进行处理之后再合并成一个Mat。在opencv2\core.hpp中定义了
  void split(InputArray m, OutputArrayOfArrays mv);
  这样一个函数可以将多通道的Mat的每个通道分离出来并保存在传入的vector中
  因此我们还需要 #include
  而使用
  void merge(InputArrayOfArrays mv, OutputArray dst);
  则可以将传入的Mat动态数组合并成一个多通道的Mat (dst)
  还拿我的QQ头像为例吧，我们来实现一个将彩色图片颜色反转的效果

#include 
#include 
#include 
#include 
using namespace cv;
using namespace std;

int main()
{
	Mat img = imread("1.jpg",IMREAD_ANYCOLOR);
	string title = "Picture";
    namedWindow(title, WINDOW_AUTOSIZE);
	vector<Mat> planes;
	split(img,planes);
	for(int i=0;i<3;i++)
		for (int r = 0; r < planes[i].rows; r++)
		{
			for (int c = 0; c < planes[i].cols; c++)
				planes[i].at<uchar>(r, c) = 255 - planes[i].at<uchar>(r, c);
		}
	Mat merge_img;
	merge(planes,merge_img);
	imshow(title, merge_img);
	waitKey(0);
	return 0;
}	

效果如下：

分离得到的planes数组中，
planes[0]是B（蓝色）通道，
planes[1]是G（绿色）通道，
planes[2]是R（红色）通道。

---

三.图像的仿射变换

在本节中，我会首先介绍图形仿射变换的数学原理，再介绍如何使用代码处理实际图像。

先来看看百度百科的定义：

仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

简单来说，我们知道图像中的每个像素点的坐标都可以用向量来表示，在一定的规则下对所有向量（向量空间）进行线性变换就可以实现视觉上图像的几何变化，如平移，放大缩小，旋转等

我们用一个向量(x,y)来表示任意像素点(u,v)变换后的坐标，则任何仿射变换都可以用以下矩阵运算来表示:
(如果不知道的话请先学习矩阵和矩阵的基本运算)

$$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)\left(\begin{array}{c}u\\ v\end{array}\right)+\left(\begin{array}{c}{a}_{13}\\ a_{23}\end{array}\right)$$

即：
$$x=a_{11}u+a_{12}v+a_{13}$$

$$y=a_{21}u+a_{22}v+a_{23}$$

上式化简一下可以直接用一次矩阵乘法来表示:
$$\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)(\ast )$$
为了方便我们约定
$$A=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ 0& 0& 1\end{array}\right)$$
并且把A叫做仿射变换矩阵，简称仿射矩阵

需要注意的是在计算机中坐标轴是这样的，左上角是原点，竖直向下是y轴正方向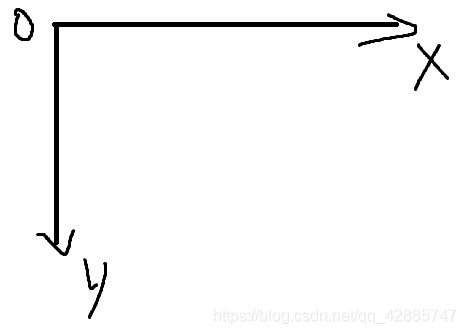

---

1. 平移

平移是最简单的仿射变换，显然在(*)式中有
$$a_{12}=a_{21}=0,$$

$$a_{11}=a_{22}=1$$
仿射矩阵为
$$\left(\begin{array}{ccc}1& 0& d_x\\ 0& 1& d_y\\ 0& 0& 1\end{array}\right)$$

因为平移后的坐标的横坐标显然与平移前的纵坐标无关，且显然不会乘以倍率，那么就只有$d_x,d_y$决定了x,y方向上的平移量，经过平移后的坐标:
$$x=u+d_x,y=v+d_y$$

---

2. 放大和缩小

首先要注意的是缩放操作有一个中心点。中心点的选取会直接影响缩放后的图形的位置，我来画个图你们就明白了：

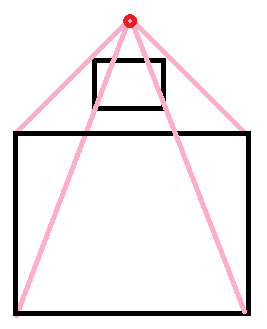
（画的有点丑不要介意）

如果以图像的左上顶点(0,0)为中心点进行缩放，我们可以使用以下仿射矩阵:

s表示scale, $s_x$ 和 $s_y$ 分别表示横纵坐标的放大倍率
缩放后的坐标：
$$x=u{s}_x,y=v{s}_y$$

如果缩放的中心点不是原点，我们可以先将图像平移到中心点与原点重合的位置，缩放后再平移回去。设缩放中心点为（x0,y0）
这一过程可以很方便地用仿射矩阵来表示:
$$\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)=\left(\begin{array}{ccc}1& 0& x_0\\ 0& 1& y_0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}{s}_x& 0& 0\\ 0& s_y& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}1& 0& -x_0\\ 0& 1& -y_0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)$$
注意先进行的变换就离原坐标(u,v,1)最近，进行一次变换就是一次矩阵左乘。

---

3.旋转