基于FPGA的Winograd CNN加速器

Winograd算法

winograd算法，它的本质就是通过减少卷积运算中的乘法，来减少计算量。我们以3x3,s=1的卷积为例，讲讲Winograd算法的具体流程。
一个$r\times s$的卷积核，和一个输入特征图进行卷积运算，得到$m\times n$的输出，我们记为：
$F(m\times n,r\times s)$
其计算量为
$\mu (F(m\times n,r\times s))=(m+r-1)\ast (n+s-1)$
和普通的直接卷积($m\ast n\ast r\ast s$)相比,计算量减少了
$\frac{m\ast n\ast r\ast s}{(m+r-1)\ast (n+s-1)}$
当$m>>r,n>>s$时，上式近似等于$r\ast s$
Winograd 的证明方法较为复杂，要用到数论中的一些知识，但是，使用起来很简单。只需要按照如下公式计算:

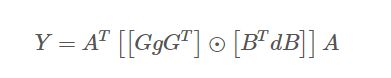
其中,$⨀$表示哈达玛乘积，$A,B,G$为相应的变换矩阵，根据输出大小和卷积核大小不同有不同的定义，但是是提前确定了的。每种输出大小和卷积核的 $A,G,B$ 具体是多少，可以通过 https://github.com/andravin/wincnn 的脚本计算。$g$为$r\times r$的卷积核，$d$为$(m+r-1)\times (m+r-1)$的输入特征块
这里只给出$m=2，r=3$的情况下，$A,B,G$相应的值：

F(2x2,3x3)更具体的计算流程可参考博客

HLS设计

因为我们加速的是VGG16网络，整个网络只包含3x3,s=1的卷积、2x2的最大池化和全连接层，因此我们只实现了两个IP核

其中，fc负责计算全连接层，WinogradConv负责计算卷积、激活函数，并且该卷积层后若还接了一个池化层，则也会进行池化运算。我们着重关注WinogradConv IP核。

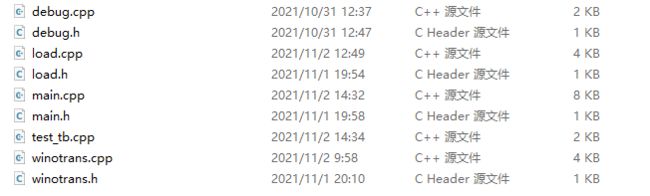
上图是该IP的代码结构，其中load.cpp用于加载和写回数据，winotrans.cpp用于计算输入特征的Winograd变换和输出特征的逆变换，在该加速器的设计中，我们对权重预先做了Winograd变换，因此权重直接加载即可，main.cpp是该设计的顶层文件，为了掩盖数据传输时间，我们在加载输入和计算之间作了乒乓操作：

void compute_output(data_t* in1,data_t* in2,data_t* in3,data_t* in4, data_t* weight1,
		data_t* weight2,data_t* weight3,data_t* weight4,
		data_t fm_out_buff[Tm][16][N][N], int m, int r, int c,int ch_in,int fsize) {
	/***************************************************/
#pragma HLS ARRAY_PARTITION variable=fm_out_buff complete dim=1
	data_t in_buff1[16][Tn][N][N];
#pragma HLS ARRAY_PARTITION variable=in_buff1 complete dim=2
	data_t in_buff2[16][Tn][N][N];
#pragma HLS ARRAY_PARTITION variable=in_buff2 complete dim=2
	data_t wt_buff1[Tm][Tn][N][N];
#pragma HLS ARRAY_PARTITION variable=wt_buff1 complete dim=2
#pragma HLS ARRAY_PARTITION variable=wt_buff1 complete dim=1
	data_t wt_buff2[Tm][Tn][N][N];
#pragma HLS ARRAY_PARTITION variable=wt_buff2 complete dim=2
#pragma HLS ARRAY_PARTITION variable=wt_buff2 complete dim=1
	//
	for(int i=0;i<16;i++)
			for(int r=0;r<N;r++)
					for(int c=0;c<N;c++){
	#pragma HLS PIPELINE II=1
						 for(int m=0;m<Tm;m++){
	#pragma HLS UNROLL
							   fm_out_buff[m][i][r][c]=(data_t)0.0;
						}
					}
	//
	bool pp=true;
	int n=0;
	load_wrapper(in1,in2,in3,in4,weight1,weight2,weight3,weight4,r,c,m,n,ch_in,fsize,in_buff1,wt_buff1);
	for (n = Tn; n < ch_in; n += Tn) {
#pragma HLS LOOP_TRIPCOUNT min=127 max=127 avg=127
        if(pp){
            load_wrapper(in1,in2,in3,in4,weight1,weight2,weight3,weight4,r,c,m,n,ch_in,fsize,in_buff2,wt_buff2);
            compute_wrapper(in_buff1, wt_buff1, fm_out_buff);
            pp=false;
        }
        else{
            load_wrapper(in1,in2,in3,in4,weight1,weight2,weight3,weight4,r,c,m,n,ch_in,fsize,in_buff1,wt_buff1);
            compute_wrapper(in_buff2, wt_buff2, fm_out_buff);
            pp=true;
        }
	}
	if(pp){
        compute_wrapper(in_buff1, wt_buff1, fm_out_buff);
	}
	else{
        compute_wrapper(in_buff2, wt_buff2, fm_out_buff);
	}
}

同时，我们也在计算和写回数据之间作了乒乓操作：

void pingpongWinogradConv(data_t* in1,data_t* in2,data_t* in3,data_t* in4, data_t* weight1,
		data_t* weight2,data_t* weight3,data_t* weight4,
		data_t* bias, data_t* out, int ch_out, int ch_in, int fsize,int pool) {
#pragma HLS INTERFACE s_axilite port=pool bundle=CTRL
#pragma HLS INTERFACE m_axi depth=100 port=bias offset=slave bundle=W max_read_burst_length=256
#pragma HLS INTERFACE s_axilite port=return bundle=CTRL
#pragma HLS INTERFACE s_axilite port=fsize bundle=CTRL
#pragma HLS INTERFACE s_axilite port=ch_in bundle=CTRL
#pragma HLS INTERFACE s_axilite port=ch_out bundle=CTRL
#pragma HLS INTERFACE m_axi depth=1536 port=out offset=slave bundle=OUT max_write_burst_length=256
#pragma HLS INTERFACE m_axi depth=4608 port=weight1 offset=slave bundle=W1 max_read_burst_length=256
#pragma HLS INTERFACE m_axi depth=768 port=in1 offset=slave bundle=IN1 max_read_burst_length=256
#pragma HLS INTERFACE m_axi depth=4608 port=weight2 offset=slave bundle=W2 max_read_burst_length=256
#pragma HLS INTERFACE m_axi depth=768 port=in2 offset=slave bundle=IN2 max_read_burst_length=256
#pragma HLS INTERFACE m_axi depth=4608 port=weight3 offset=slave bundle=W3 max_read_burst_length=256
#pragma HLS INTERFACE m_axi depth=768 port=in3 offset=slave bundle=IN3 max_read_burst_length=256
#pragma HLS INTERFACE m_axi depth=4608 port=weight4 offset=slave bundle=W4 max_read_burst_length=256
#pragma HLS INTERFACE m_axi depth=768 port=in4 offset=slave bundle=IN4 max_read_burst_length=256
	//
	data_t fm_out_buff1[Tm][16][N][N];
#pragma HLS ARRAY_PARTITION variable=fm_out_buff1 complete dim=1
	data_t fm_out_buff2[Tm][16][N][N];
#pragma HLS ARRAY_PARTITION variable=fm_out_buff2 complete dim=1
	data_t bias_buff[1024/Tm][Tm];
#pragma HLS ARRAY_PARTITION variable=bias_buff complete dim=2
	int m, i, j, next_m, next_i, next_j;
	m = i = j = 0;
	bool pingpong = true;
	//
	memcpy((data_t*)bias_buff,(const data_t*)bias,sizeof(data_t)*ch_out);
	compute_output(in1,in2,in3,in4, weight1,weight2,weight3,weight4, fm_out_buff1, m,i,j ,ch_in, fsize);
	while (true) {
#pragma HLS LOOP_TRIPCOUNT min=255 max=255 avg=255
		next_block(i, j, m, next_i, next_j, next_m, fsize, ch_out);
		if (next_m + Tm > ch_out)
			break;
		if (pingpong) {
			compute_output(in1,in2,in3,in4, weight1,weight2,weight3,weight4, fm_out_buff2, next_m, next_i, next_j, ch_in, fsize);
			write_back(out, fm_out_buff1,bias_buff[m/Tm], m, i, j, fsize,pool);
			pingpong = false;
		}
		else {
			compute_output(in1,in2,in3,in4, weight1,weight2,weight3,weight4, fm_out_buff1, next_m, next_i, next_j, ch_in, fsize);
			write_back(out, fm_out_buff2,bias_buff[m/Tm], m, i, j, fsize,pool);
			pingpong = true;
		}
		m = next_m;
		i = next_i;
		j = next_j;
	}
	if (pingpong) {
		write_back(out, fm_out_buff1, bias_buff[m/Tm],m, i, j, fsize,pool);
	}
	else {
		write_back(out, fm_out_buff2,bias_buff[m/Tm], m, i, j, fsize,pool);
	}
}

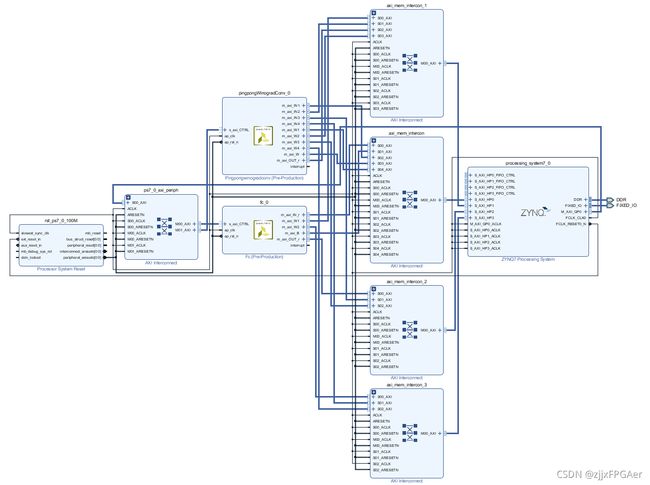
Block Design

SDK设计

我们将图片和权重存在SD卡中，以供zynq的ps端读取，读取完成后，ps通过调用IP核，启动PL端的加速器。以下是源代码的结构

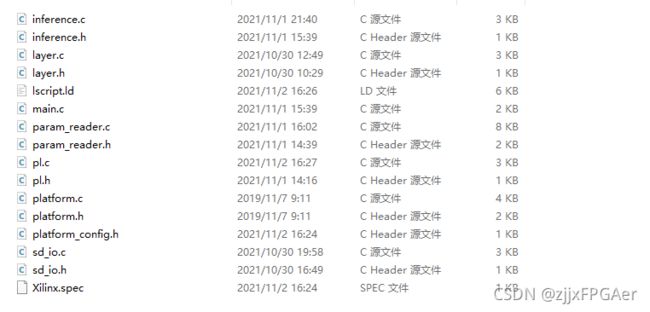
sd_io.c，param_reader.c用于从SD卡读取权重和图片，pl.c用于调用PL端IP核进行加速计算,layer.c,inference.c为PL端推理代码，main.c为主函数所在文件
以下是推理部分代码，我们设置了3个buffer：out1q,out2q,out3q，用于存储中间结果，同时通过memalign函数实现地址的8字节对齐，以配合HLS代码中的大位宽读写。

void inference_test(XPingpongwinogradconv *hls_conv,XFc *hls_fc,FData* fdata,FWeight* fw){
    //
    short* out1q=(short*)memalign(8,1000000*sizeof(short));
    short* out2q=(short*)memalign(8,1000000*sizeof(short));
    short* out3q=(short*)memalign(8,1000000*sizeof(short));
    int correct=0;
    XTime tEnd, tCur;
    u32 tUsed;
    for(int i=0;i<100;i++){
    	printf("i=%d\n",i);
    	XTime_GetTime(&tCur);
        //block1,32x32,64
        pl_conv(hls_conv,fdata->images+i*32*32*3,fw->winoweight[0],fw->bias[0],out1q,3,64,32,0);
        pl_conv(hls_conv,out1q,fw->winoweight[1],fw->bias[1],out3q,64,64,32,1);
        //block2,16x16,128
        pl_conv(hls_conv,out3q,fw->winoweight[2],fw->bias[2],out2q,64,128,16,0);
        pl_conv(hls_conv,out2q,fw->winoweight[3],fw->bias[3],out3q,128,128,16,1);
        //block3,8x8,256
        pl_conv(hls_conv,out3q,fw->winoweight[4],fw->bias[4],out1q,128,256,8,0);
        pl_conv(hls_conv,out1q,fw->winoweight[5],fw->bias[5],out2q,256,256,8,0);
        pl_conv(hls_conv,out2q,fw->winoweight[6],fw->bias[6],out1q,256,256,8,0);
        //block4,8x8,512
        pl_conv(hls_conv,out1q,fw->winoweight[7],fw->bias[7],out2q,256,512,8,0);
        pl_conv(hls_conv,out2q,fw->winoweight[8],fw->bias[8],out1q,512,512,8,0);
        pl_conv(hls_conv,out1q,fw->winoweight[9],fw->bias[9],out2q,512,512,8,0);
        //block5,8x8,512
        pl_conv(hls_conv,out2q,fw->winoweight[10],fw->bias[10],out1q,512,512,8,0);
        pl_conv(hls_conv,out1q,fw->winoweight[11],fw->bias[11],out2q,512,512,8,0);
        pl_conv(hls_conv,out2q,fw->winoweight[12],fw->bias[12],out1q,512,512,8,0);
        pl_fc(hls_fc,out1q,fw->weight[13],fw->bias[13],out2q);
        //argmax
        short max=-10000;
        int max_idx=-1;
        for(int k=0;k<10;k++){
            if(out2q[k]>max){
                max=out2q[k];
                max_idx=k;
            }
        }
        XTime_GetTime(&tEnd);		//��ȡ����ʱ��
		tUsed = ((tEnd-tCur)*1000000)/(COUNTS_PER_SECOND); //����õ���ʱus
		printf("time elapsed is %d us\r\n",tUsed);
        //check
        if(max_idx==fdata->labels[i]){
            printf("right\n");
            correct++;
        }
        else
            printf("error\n");

    }
    printf("test acc is %f \%",correct/100.0);
}

上板测试结果

可以看到，单张图片推理用时285ms左右。