QDD基础网络系列（1）——ShuffleNet

论文地址https://arxiv.org/pdf/1707.01083.pdf

前言：

最近感觉自己写的博客，比较肤浅浮于表面，所以决定要写一个系列，没有想太多，但是希望能够用两三个月的时间，把这个系列介绍好，算给自己打基础了就。

正文

相信咱们这个领域的应该都知道前几天Geoffrey Hinton， Yann LeCun，和Yoshua Bengio共同获得了2019年的图灵奖，心疼Ng三秒，毕竟忙着和媳妇儿开公司呢。言归正传被近些年来随着神经网络的崛起，网络的层数是越来越深，结构是越来越复杂，需要的计算资源也是开始动辄出现几百块的需求了。那在这种情况下，工业界就说，如果我需要在我的手机上，cpu端或者ARM框架下使用，怎么办。这就有很多的解决办法，比如剪支，比如模型压缩，或者直接设计小体量的模型。

于是这篇ShuffleNet是旷世的孙老师他们提出的一种计算高效的CNN模型，以及近期提出的Mobilenet和SqueezeNet等模型就提供了一种可行的解决方案。这几个网络可以应用于移动端，但是shufflenet在性能以及速度方面比较其他的网络都有较大的提升。

那么到底是如何实现ShuffleNet的呢？作者一共提出了这两个问题，解决了这两个问题就能弄明白这个网络了：

一 pointwise group convolution

1）我相信大部分同学看到这个词和我本人一样是蒙蔽的，这里面有很大的讲究，让我来慢慢讲给你听。

首先这个pointwise convolution，又称为逐点卷积，深度可分离卷积。

这是常见的卷积形式：举个例子，假设有一个3×3大小的卷积层，要求输入为16通道、输出为32通道。那么显而易见我们就需要32个3*3的卷积核，每个卷积核携带的参数量是3*3*16,那么这个卷积过程所需要的参数量即使(3×3×16)×32 =4068

而深度可分离卷积（逐点卷积）可以分为如上图所示的两个过程：①用16个3×3大小的卷积核（1通道）分别与输入的16通道的数据做卷积（这里使用了16个1通道的卷积核，输入数据的每个通道用1个3×3的卷积核卷积），得到了16个通道的特征图，我们说该步操作是depthwise（逐层）的，在叠加16个特征图之前，②接着用32个1×1大小的卷积核（16通道）在这16个特征图进行卷积运算，将16个通道的信息进行融合（用1×1的卷积进行不同通道间的信息融合），我们说该步操作是pointwise（逐像素）的。这样我们可以算出整个过程使用了3×3×16+（1×1×16）×32 =656个参数。

2）group convolution

下面开始介绍group convolution：分组卷积，最早在AlexNet中出现，由于当时的硬件资源有限，训练AlexNet时卷积操作不能全部放在同一个GPU处理，因此作者把feature maps分给多个GPU分别进行处理，最后把多个GPU的结果进行融合。

这是一般我们看到的卷积的过程，一般的卷积过程是对于整个图像进行的，输入H1×W1×C1；而卷积核大小为h1×w1，一共有C2个，然后卷积得到的输出数据就是H2×W2×C2。这里我们假设输出和输出的分辨率是不变的。我们可以看到这是把整个图片一次性读入，对于系统的存储会有一些要求。

上图所示就是分组卷积的示意图：图中将输入数据分成了2组（组数为g），需要注意的是，这种分组只是在深度上进行划分，即某几个通道编为一组，这个具体的数量由（C1/g）决定。因为输出数据的改变，相应的，卷积核也需要做出同样的改变。即每组中卷积核的深度也就变成了（C1/g），而卷积核的大小是不需要改变的，此时每组的卷积核的个数就变成了（C2/g）个，而不是原来的C2了。

从一个具体的例子来看，Group conv本身就极大地减少了参数。比如当输入通道为256，输出通道也为256，kernel size为3×3，不做Group conv参数为256×3×3×256。实施分组卷积时，若group为8，每个group的input channel和output channel均为32，参数为8×32×3×3×32，是原来的八分之一。而Group conv最后每一组输出的feature maps应该是以concatenate的方式组合。
Alex认为group conv的方式能够增加 filter之间的对角相关性，而且能够减少训练参数，不容易过拟合，这类似于正则的效果。

二 channel shuffle

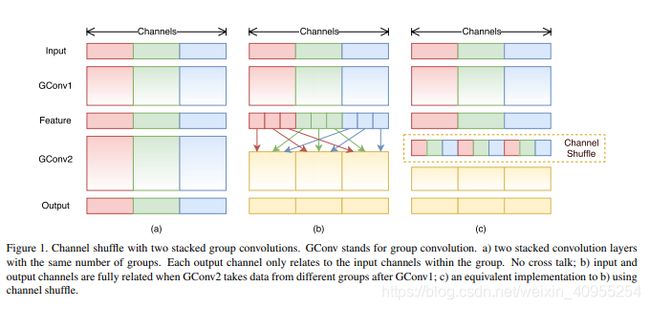
分组卷积存在另外一个弊端，如图1-a所示，其中GConv是group convolution，这里分组数是3。可以看到当堆积GConv层后一个问题是不同组之间的特征图是不通信的，这就好像分了三个互不相干的路，大家各走各的，这目测会降低网络的特征提取能力

为了实现通道间的信息交流，规避上述弊端：如图1-b所示，你可以对group convolution之后的特征图进行“重组”，这样可以保证接下了采用的group convolution其输入来自不同的组，因此信息可以在不同组之间流转。这个操作等价于图2-c，即group convolution之后对channels进行shuffle，但并不是随机的，其实是“均匀地打乱”。在程序上实现channel shuffle是非常容易的：假定将输入层分为  组，总通道数为  ，首先你将通道那个维度拆分为  两个维度，然后将这两个维度转置变成  ，最后重新reshape成一个维度。channel shuffle操作还有一个好处是能保证端到端的训练。

这是我看到网上画的一张比较有意思的图（我借用一下，如有侵权，联系删，末尾引用）

好啦，重点内容就将这么多啦

我知道你们在等代码：https://github.com/MG2033/ShuffleNet

里面还有几个bug，调不出来的私聊我啦。

拜拜

参考：

1卷积原理：几种常用的卷积（标准卷积、深度卷积、组卷积、扩展卷积、反卷积）

2 CNN模型之ShuffleNet

3 轻量级网络--ShuffleNet论文解读

学术交流可以关注我的公众号，后台留言，粉丝不多，看到必回。卑微小钱在线祈求