轻量级网络——ShuffleNetV2
文章目录
- 1.ShuffleNetV2的介绍
- 2.ShuffleNetV2的四条实用指南
-
- G1) Equal channel width minimizes memory access cost (MAC)
- G2) Excessive group convolution increases MAC
- G3) Network fragmentation reduces degree of parallelism
- G4) Element-wise operations are non-negligible
- 3.ShuffleNetV2的结构
-
- Channel Split and ShuffleNet V2
- Analysis of Network Accuracy
- 4.ShuffleNetV2的性能统计
- 5.ShuffleNetV2的pytorch实现
回顾: 轻量级网络——ShuffleNetV1
paper链接:ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design
关键内容:
ShuffleNetV2中提出了一个关键点,之前的轻量级网络都是通过计算网络复杂度的一个间接度量,即FLOPs为指导。通过计算浮点运算量来描述轻量级网络的快慢。但是从来不直接考虑运行的速度。在移动设备中的运行速度不仅仅需要考虑FLOPs,还需要考虑其他的因素,比如内存访问成本(memory access cost)和平台特点(platform characterics)。
所以,ShuffleNetV2直接通过控制不同的环境来直接测试网络在设备上运行速度的快慢,而不是通过FLOPs来判断。
1.ShuffleNetV2的介绍
在之间轻量级网络的发展中,为了度量计算复杂度,一个广泛使用的度量标准是浮点运算的数量(FLOPs)。然而,FLOPs是一个间接的指标。这值是一个近似,但通常不等同于我们真正关心的直接指标,比如速度或延迟。
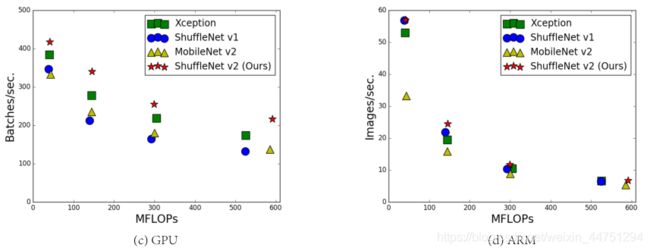
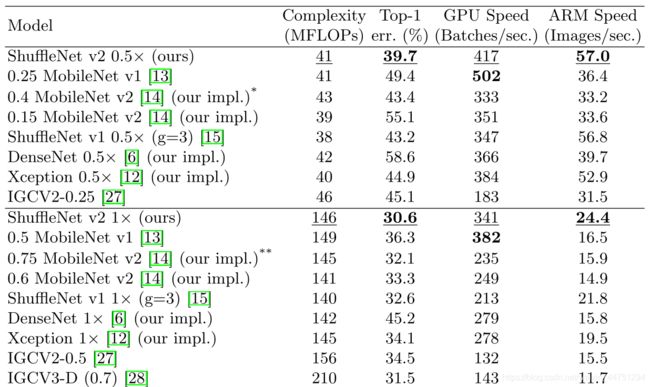
如上图,具有相似FLOPs的网络却具有不同的网速。因此,使用FLOPs作为计算复杂度的唯一指标是不够的,可能会导致次优化设计。
间接(FLOPs)和直接(速度)指标之间的差异可以归结为两个主要原因。首先,FLOPs没有考虑到几个对速度有相当大影响的重要因素。其中一个因素就是内存访问成本(MAC)。在某些操作(如组卷积)中,这种代价构成了运行时的很大一部分。它可能会成为具有强大计算能力的设备的瓶颈,例如gpu。在设计网络体系结构时,不应该简单地忽略这个代价。另一个是并行度。在相同的FLOPs下,具有高并行度的模型可能比另一个具有低并行度的模型快得多。
其次,由于平台的不同是,使用相同的FLOPs操作可能有不同的运行时间。我们不能肯定地认为3 × 3 conv比1 × 1 conv慢9倍。因为最新的CUDNN库专门针对3 × 3 conv进行了优化。
因为,ShuffleNetv2提出了设计应该考虑两个原则:
- 应该使用直接度量(如速度)而不是间接度量(如FLOPs。
- 这些指标应该在目标平台上进行评估。(也就是实事求是)
然后,ShuffleNetv2根据这两个原则,提出了四种有效的网络设计原则:
- G1: Equal channel width minimizes memory access cost (MAC)
- G2: Excessive group convolution increases MAC
- G3: Network fragmentation reduces degree of parallelism
- G4: Element-wise operations are non-negligible
在计算复杂度为40M FLOPs的情况下,ShuffleNet v2的精度分别比ShuffleNet v1和MobileNet v2高3.5%和3.7%
2.ShuffleNetV2的四条实用指南
整个运行时被分解为不同的操作,如图2所示。我们注意到FLOPs度量只考虑了卷积部分。虽然这一部分消耗的时间最多,但其他操作包括data I/O、data shuffle和element-wise operations(AddTensor、ReLU等)也占用了相当多的时间。因此,FLOPs并不是对实际运行时的足够准确的估计。

G1) Equal channel width minimizes memory access cost (MAC)
当卷积层的输入特征矩阵与输出特征矩阵channel相等时MAC最小(保持FLOPs不变时)
现代网络通常采用depthwise separable convolutions ,其中pointwise convolution(即1 × 1卷积)占了复杂性的大部分。研究了1 × 1卷积的核形。形状由两个参数指定:输入通道c1和输出通道c2的数量。设h和w为feature map的空间大小,1 × 1卷积的FLOPs为 B = h ∗ w ∗ c 1 ∗ c 2 B = h*w*c_{1}*c_{2} B=h∗w∗c1∗c2.内存访问成本(MAC),即内存访问操作数,为
M A C = h w ( c 1 + c 2 ) + c 1 ∗ c 2 MAC = hw(c_{1}+c_{2})+c_{1}*c_{2} MAC=hw(c1+c2)+c1∗c2
这两个术语分别对应于输入/输出特性映射的内存访问和内核权重。其实这条公式可以看成由三个部分组成:第一部分是 h w c 1 hwc_{1} hwc1,对应的是输入特征矩阵的内存消耗;第二部分是 h w c 2 hwc_{2} hwc2,对应的是输出特征矩阵的内存消耗。第三部分是 c 1 ∗ c 2 c_{1}*c_{2} c1∗c2,对应的是卷积核的内存消耗。
由均值不等式 c 1 + c 2 2 ≥ c 1 c 2 \frac{c_{1}+c_{2}}{2} ≥ \sqrt{c_{1}c_{2}} 2c1+c2≥c1c2得出:
M A C ≥ 2 h w c 1 c 2 + c 1 c 2 ≥ 2 h w B + B h w \begin{aligned} MAC &≥ 2hw\sqrt{c_{1}c_{2}}+c_{1}c_{2} \\ &≥2\sqrt{hwB} + \frac{B}{hw} \end{aligned} MAC≥2hwc1c2+c1c2≥2hwB+hwB
其中: B = h w c 1 c 2 B = hwc_{1}c_{2} B=hwc1c2因此,MAC有一个由FLOPs给出的下限。当输入和输出通道的数量相等时,它达到下界。
为了验证上述结论,进行了如下实验。一个基准网络由10个构件重复堆叠而成。每个块包含两个卷积层。第一个卷积层由c1输入通道和c2输出通道组成,第二个则相反,输入通道是c2输出通道是c1。

表1通过改变比率c1: c2报告了在固定总FLOPs时的运行速度。可见,当c1: c2接近1:1时,MAC变小,网络评估速度加快。
G2) Excessive group convolution increases MAC
当GConv的groups增大时(保持FLOPs不变时),MAC也会增大
组卷积是现代网络体系结构的核心。它通过将所有通道之间的密集卷积改变为稀疏卷积(仅在通道组内)来降低计算复杂度(FLOPs)。一方面,它允许在一个固定的FLOPs下使用更多的channels,并增加网络容量(从而提高准确性)。然而,另一方面,增加的通道数量导致更多的MAC。
M A C = h w ( c 1 + c 2 ) + c 1 c 2 g = h w c 1 + B g c 1 + B h w \begin{aligned} MAC &= hw(c_{1}+c_{2}) + \frac{c_{1}c_{2}}{g} \\ &= hwc_{1} + \frac{Bg}{c_{1}} + \frac{B}{hw} \end{aligned} MAC=hw(c1+c2)+gc1c2=hwc1+c1Bg+hwB
其中g为分组数, B = h w c 1 c 2 / g B = hwc_{1}c_{2}/g B=hwc1c2/g为FLOPs。不难看出,给定固定的输入形状c1× h × w,计算代价B, MAC随着g的增长而增加

很明显,使用大量的组数会显著降低运行速度。例如,在GPU上使用8group比使用1group(标准密集卷积)慢两倍以上,在ARM上慢30%。这主要是由于MAC的增加。所以使用比较大组去进行组卷积是不明智的。对速度会造成比较大的影响。
G3) Network fragmentation reduces degree of parallelism
网络设计的碎片化程度越高,速度越慢
虽然这种碎片化结构已经被证明有利于提高准确性,但它可能会降低效率,因为它对GPU等具有强大并行计算能力的设备不友好。它还引入了额外的开销,比如内核启动和同步。

为了量化网络分片如何影响效率,我们评估了一系列不同分片程度的网络块。具体来说,每个构造块由1到4个1 × 1的卷积组成,这些卷积是按顺序或平行排列的。每个块重复堆叠10次。块结构上图所示。
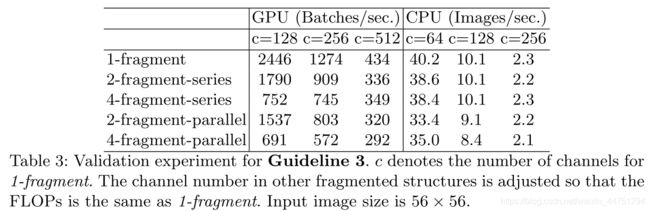
表3的结果显示,在GPU上碎片化明显降低了速度,如4-fragment结构比1-fragment慢3倍。在ARM上,速度降低相对较小。
一个比较容易理解为啥4-fragment结构比较慢的说法是,4-fragment结构需要等待每个分支处理完之后再进行下一步的操作,也就是需要等待最慢的那一个。所以,效率是比较低的。
G4) Element-wise operations are non-negligible
Element-wise操作带来的影响是不可忽视的

轻量级模型中,元素操作占用了相当多的时间,特别是在GPU上。这里的元素操作符包括ReLU、AddTensor、AddBias等。将depthwise convolution作为一个element-wise operator,因为它的MAC/FLOPs比率也很高
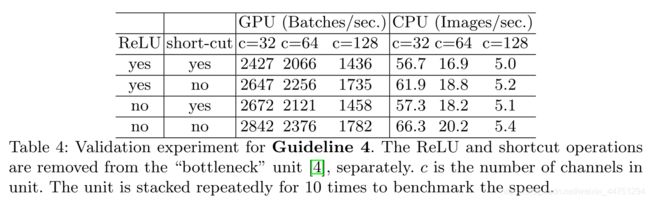
可以看见表4中报告了不同变体的运行时间。我们观察到,在移除ReLU和shortcut后,GPU和ARM都获得了大约20%的加速。
这里主要突出的是,这些操作会比我们想象当中的要耗时。
总结:
基于上述准则和实证研究,我们得出结论:一个高效的网络架构应该
- 1)使用“平衡”卷积(等信道宽度);
- 2)了解使用群卷积的代价;
- 3)降低碎片化程度;
- 4)减少元素操作。
这些理想的属性依赖于平台特性(如内存操作和代码优化),这些特性超出了理论FLOPs。在实际的网络设计中应该考虑到这些因素。而轻量级神经网络体系结构最新进展大多基于FLOPs的度量,没有考虑上述这些特性。
3.ShuffleNetV2的结构
Channel Split and ShuffleNet V2
回顾ShuffleNetV1的结构,其主要采用了两种技术:pointwise group convolutions与bottleneck-like structures。然后引入“channel shuffle”操作,以实现不同信道组之间的信息通信,提高准确性。
both pointwise group convolutions与bottleneck structures均增加了MAC,与G1和G2不符合。这一成本是不可忽视的,特别是对于轻型机型。此外,使用太多group违反G3。shortcut connection中的元素element-wise add操作也是不可取的,违反了G4。因此,要实现高模型容量和高效率,关键问题是如何在不密集卷积和不过多分组的情况下,保持大量的、同样宽的信道。
其中图c对应stride=1的情况,图d对应stride=2的情况
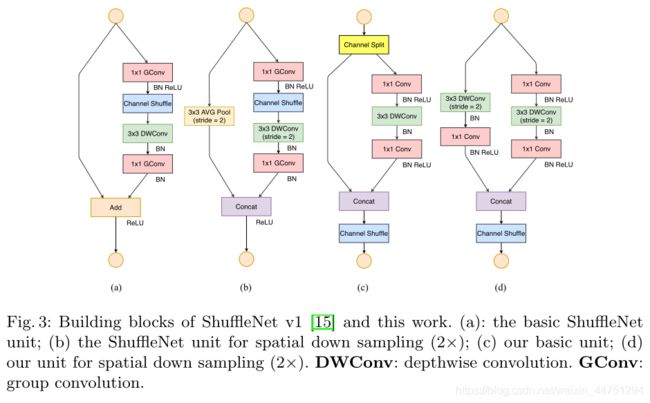
为此,ShuffleNetV2做出了改进,如图( c )所示,在每个单元的开始,c特征通道的输入被分为两个分支(在ShuffleNetV2中这里是对channels均分成两半)。根据G3,不能使用太多的分支,所以其中一个分支不作改变,另外的一个分支由三个卷积组成,它们具有相同的输入和输出通道以满足G1。两个1 × 1卷积不再是组卷积,而改变为普通的1x1卷积操作,这是为了遵循G2(需要考虑组的代价)。卷积后,两个分支被连接起来,而不是相加(G4)。因此,通道的数量保持不变(G1)。然后使用与ShuffleNetV1中相同的“channels shuffle”操作来启用两个分支之间的信息通信。需要注意,ShuffleNet v1中的“Add”操作不再存在。像ReLU和depthwise convolutions 这样的元素操作只存在于一个分支中。
对于空间下采样,单元稍作修改,移除通道分离操作符。因此,输出通道的数量增加了一倍。具体结构见图(d)。所提出的构建块( c )( d )以及由此产生的网络称为ShuffleNet V2。基于上述分析,我们得出结论,该体系结构设计是高效的,因为它遵循了所有的指导原则。积木重复堆叠,构建整个网络。
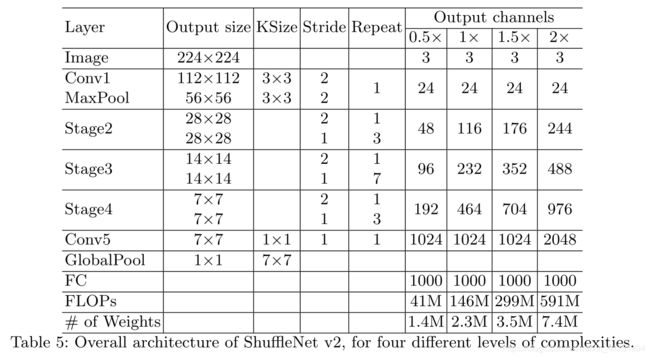
总体网络结构类似于ShuffleNet v1,如表所示。只有一个区别:在全局平均池之前增加了一个1 × 1的卷积层来混合特性,这在ShuffleNet v1中是没有的。与下图类似,每个block中的通道数量被缩放,生成不同复杂度的网络,标记为0.5x,1x,1.5x,2x
Analysis of Network Accuracy
ShuffleNet v2不仅高效,而且准确。主要有两个原因:
- 首先,每个构建块的高效率使使用更多的特征通道和更大的网络容量成为可能
- 第二,在每个块中,有一半的特征通道直接穿过该块并加入下一个块。这可以看作是一种特性重用,就像DenseNet和CondenseNet的思想一样。
4.ShuffleNetV2的性能统计
5.ShuffleNetV2的pytorch实现
参考github代码:代码与ShuffleNetV1类似
import torch
import torch.nn as nn
import torchvision
# 3x3DW卷积(含激活函数)
def Conv3x3BNReLU(in_channels,out_channels,stride,groups):
return nn.Sequential(
nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=3, stride=stride, padding=1, groups=groups),
nn.BatchNorm2d(out_channels),
nn.ReLU6(inplace=True)
)
# 3x3DW卷积(不激活函数)
def Conv3x3BN(in_channels,out_channels,stride,groups):
return nn.Sequential(
nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=3, stride=stride, padding=1, groups=groups),
nn.BatchNorm2d(out_channels)
)
# 1x1PW卷积(含激活函数)
def Conv1x1BNReLU(in_channels,out_channels):
return nn.Sequential(
nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=1, stride=1),
nn.BatchNorm2d(out_channels),
nn.ReLU6(inplace=True)
)
# 1x1PW卷积(不含激活函数)
def Conv1x1BN(in_channels,out_channels):
return nn.Sequential(
nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=1, stride=1),
nn.BatchNorm2d(out_channels)
)
# 划分channels: dim默认为0,但是由于channnels位置在1,所以传参为1
class HalfSplit(nn.Module):
def __init__(self, dim=0, first_half=True):
super(HalfSplit, self).__init__()
self.first_half = first_half
self.dim = dim
def forward(self, input):
# 对input的channesl进行分半操作
splits = torch.chunk(input, 2, dim=self.dim) # 由于shape=[b, c, h, w],对于dim=1,针对channels
return splits[0] if self.first_half else splits[1] # 返回其中的一半
# channels shuffle增加组间交流
class ChannelShuffle(nn.Module):
def __init__(self, groups):
super(ChannelShuffle, self).__init__()
self.groups = groups
def forward(self, x):
'''Channel shuffle: [N,C,H,W] -> [N,g,C/g,H,W] -> [N,C/g,g,H,w] -> [N,C,H,W]'''
N, C, H, W = x.size()
g = self.groups
return x.view(N, g, int(C / g), H, W).permute(0, 2, 1, 3, 4).contiguous().view(N, C, H, W)
# ShuffleNet的基本单元
class ShuffleNetUnits(nn.Module):
def __init__(self, in_channels, out_channels, stride, groups):
super(ShuffleNetUnits, self).__init__()
self.stride = stride
# 如果stride = 2,由于主分支需要加上从分支的channels,为了两者加起来等于planes,所以需要先减一下
if self.stride > 1:
mid_channels = out_channels - in_channels
# 如果stride = 2,mid_channels是一半,直接除以2即可
else:
mid_channels = out_channels // 2
in_channels = mid_channels
# 进行两次切分,一次接受一半,一次接受另外一半
self.first_half = HalfSplit(dim=1, first_half=True) # 对channels进行切半操作, 第一次分: first_half=True
self.second_split = HalfSplit(dim=1, first_half=False) # 返回输入的另外一半channesl,两次合起来才是完整的一份channels
# 两个结构的主分支都是一样的,只是3x3DW卷积中的stride不一样,所以可以调用同样的self.bottleneck,stride会自动改变
self.bottleneck = nn.Sequential(
Conv1x1BNReLU(in_channels, in_channels), # 没有改变channels
Conv3x3BN(in_channels, mid_channels, stride, groups), # 升维
Conv1x1BNReLU(mid_channels, mid_channels) # 没有改变channels
)
# 结构(d)的从分支,3x3的DW卷积——>1x1卷积
if self.stride > 1:
self.shortcut = nn.Sequential(
Conv3x3BN(in_channels=in_channels, out_channels=in_channels, stride=stride, groups=groups),
Conv1x1BNReLU(in_channels, in_channels)
)
self.channel_shuffle = ChannelShuffle(groups)
def forward(self, x):
# stride = 2: 对于结构(d)
if self.stride > 1:
x1 = self.bottleneck(x) # torch.Size([1, 220, 28, 28])
x2 = self.shortcut(x) # torch.Size([1, 24, 28, 28])
# 两个分支作concat操作之后, 输出的channels便为224,与planes[0]值相等
# out输出为: torch.Size([1, 244, 28, 28])
# stride = 1: 对于结构(c)
else:
x1 = self.first_half(x) # 一开始直接将channels等分两半,x1称为主分支的一半,此时的x1: channels = 112
x2 = self.second_split(x) # x2称为输入的另外一半channels: 此时x2:: channels = 112
x1 = self.bottleneck(x1) # 结构(c)的主分支处理
# 两个分支作concat操作之后, 输出的channels便为224,与planes[0]值相等
# out输出为: torch.Size([1, 244, 28, 28])
out = torch.cat([x1, x2], dim=1) # torch.Size([1, 244, 28, 28])
out = self.channel_shuffle(out) # ShuffleNet的精髓
return out
class ShuffleNetV2(nn.Module):
# shufflenet_v2_x2_0: planes = [244, 488, 976] layers = [4, 8, 4]
# shufflenet_v2_x1_5: planes = [176, 352, 704] layers = [4, 8, 4]
def __init__(self, planes, layers, groups, is_shuffle2_0, num_classes=5):
super(ShuffleNetV2, self).__init__()
# self.groups = 1
self.groups = groups
# input: torch.Size([1, 3, 224, 224])
self.stage1 = nn.Sequential(
# 结构图中,对于conv1与MaxPool的stride均为2
Conv3x3BNReLU(in_channels=3, out_channels=24, stride=2, groups=1), # torch.Size([1, 24, 112, 112])
nn.MaxPool2d(kernel_size=3, stride=2, padding=1) # torch.Size([1, 24, 56, 56])
)
self.stage2 = self._make_layer(24, planes[0], layers[0], True) # torch.Size([1, 244, 28, 28])
self.stage3 = self._make_layer(planes[0], planes[1], layers[1], False) # torch.Size([1, 488, 14, 14])
self.stage4 = self._make_layer(planes[1], planes[2], layers[2], False) # torch.Size([1, 976, 7, 7])
# 0.5x / 1x / 1.5x 输出为1024, 2x 输出为 2048
self.conv5 = nn.Conv2d(in_channels=planes[2], out_channels=1024*is_shuffle2_0, kernel_size=1, stride=1)
self.global_pool = nn.AdaptiveAvgPool2d(1) # torch.Size([1, 976, 1, 1])
self.dropout = nn.Dropout(p=0.2) # 丢失概率为0.2
# 0.5x / 1x / 1.5x 输入为1024, 2x 输入为 2048
self.linear = nn.Linear(in_features=1024*is_shuffle2_0, out_features=num_classes)
self.init_params()
# 此处的is_stage2作用不大,以为均采用3x3的DW卷积,也就是group=1的组卷积
def _make_layer(self, in_channels, out_channels, block_num, is_stage2):
layers = []
# 在ShuffleNetV2中,每个stage的第一个结构的stride均为2;此stage的其余结构的stride均为1.
# 对于stride =2 的情况,对应结构(d): 一开始无切分操作,主分支经过1x1——>3x3——>1x1,从分支经过3x3——>1x1,两个分支作concat操作
layers.append(ShuffleNetUnits(in_channels=in_channels, out_channels=out_channels, stride= 2, groups=1 if is_stage2 else self.groups))
# 对于stride = 1的情况,对应结构(c): 一开始就切分channel,主分支经过1x1——>3x3——>1x1再与shortcut进行concat操作
for idx in range(1, 2):
layers.append(ShuffleNetUnits(in_channels=out_channels, out_channels=out_channels, stride=1, groups=self.groups))
return nn.Sequential(*layers)
# 何凯明的方法初始化权重
def init_params(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight)
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d) or isinstance(m, nn.Linear):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
# input: torch.Size([1, 3, 224, 224])
def forward(self, x):
x = self.stage1(x) # torch.Size([1, 24, 56, 56])
x = self.stage2(x) # torch.Size([1, 244, 28, 28])
x = self.stage3(x) # torch.Size([1, 488, 14, 14])
x = self.stage4(x) # torch.Size([1, 976, 7, 7])
x = self.conv5(x) # torch.Size([1, 2048, 7, 7])
x = self.global_pool(x) # torch.Size([1, 2048, 1, 1])
x = x.view(x.size(0), -1) # torch.Size([1, 2048])
x = self.dropout(x)
out = self.linear(x) # torch.Size([1, 5])
return out
def shufflenet_v2_x2_0(**kwargs):
planes = [244, 488, 976]
layers = [4, 8, 4]
model = ShuffleNetV2(planes, layers, 1, 2)
return model
def shufflenet_v2_x1_5(**kwargs):
planes = [176, 352, 704]
layers = [4, 8, 4]
model = ShuffleNetV2(planes, layers, 1, 1)
return model
def shufflenet_v2_x1_0(**kwargs):
planes = [116, 232, 464]
layers = [4, 8, 4]
model = ShuffleNetV2(planes, layers, 1, 1)
return model
def shufflenet_v2_x0_5(**kwargs):
planes = [48, 96, 192]
layers = [4, 8, 4]
model = ShuffleNetV2(planes, layers, 1, 1)
return model
if __name__ == '__main__':
model = shufflenet_v2_x2_0()
# model = shufflenet_v2_x1_5()
# model = shufflenet_v2_x1_0()
# model = shufflenet_v2_x0_5()
# print(model)
input = torch.randn(1, 3, 224, 224)
out = model(input)
print(out.shape)
torch.save(model.state_dict(), "shufflenet_v2_x2_0.mdl")
参考资料:
https://www.bilibili.com/video/BV15y4y1Y7SY
https://arxiv.org/pdf/1807.11164.pdf