机器学习（四）：逻辑回归实战——信用卡欺诈检测

1、数据

数据链接在此
https://pan.baidu.com/s/1APgU4cTAaM9zb8_xAIc41Q密码: xgg7

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
data = pd.read_csv("creditcard.csv")
data.head()

• time表示交易持续的时间；
• v1、v2、v3…v28表示特征；
• Amount表示交易额金额；
• Class 这列0代表是正常样本,1代表异常样本

count_classes = pd.value_counts(data['Class'], sort = True).sort_index() # 对class这列出现的数字进行统计
count_classes.plot(kind = 'bar') #  画条形图
plt.title('Fraud class histogram')
plt.xlabel("Class")
plt.ylabel("Frequency")

2、样本不均衡解决方案

可以看到正常样本0很多，异常样本1非常少，这种样本数据不均衡，可以有两种解决方案。
（1）下采样。将数据变得同样少，可以随机选择0的数据，变得和1的数据一样多。
（2）过采样。将数据变得同样多，对1的样本数据生成数列，让生成的数据与0的样本数据一样多。

首先需要将Amount那一列数据处理成（-1，1）区间的

from sklearn.preprocessing import StandardScaler
# reshape(-1,1)前面的-1可自动识别有几行，第二个1表示一列
data['normAmount'] = StandardScaler().fit_transform(data['Amount'].reshape(-1, 1))
data = data.drop(['Time','Amount'],axis=1)# 丢弃这两列
data.head()

举例：下采样

# ix / loc 可以通过行号和行标签进行索引
X = data.ix[:, data.columns != 'Class']# 前面的“：”表示所有行，后面表示列名不为Class的所有列
y = data.ix[:, data.columns == 'Class']
#class为1的有多少个
number_records_fraud = len(data[data.Class == 1])
fraud_indices = np.array(data[data.Class == 1].index)

normal_indices = data[data.Class == 0].index
# 随机选择和class为1的个数相同的class为0的行
random_normal_indices = np.random.choice(normal_indices,number_records_fraud,replace=False)
random_normal_indices = np.array(random_normal_indices)

# 合并数据
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])

under_sample_data = data.iloc[under_sample_indices,:]

X_undersample = under_sample_data.ix[:,under_sample_data.columns != 'Class']
y_undersample = under_sample_data.ix[:,under_sample_data.columns == 'Class']

print("Percentage of normal transactions: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
print("Percentage of fraud transactions: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
print("Total number of transactions in resampled data: ", len(under_sample_data))

输出结果：

Percentage of normal transactions:  0.5
Percentage of fraud transactions:  0.5
Total number of transactions in resampled data:  984

3、交叉验证

它的主体思想是将原始数据进行分组，一部分作为训练集，一部分作为验证集。利用训练集训练出模型，利用验证集来测试模型，以评估分类模型的性能。

K折交叉验证：这里的k折是把数据分为k组，将k-1组作为训练集训练出一个模型，然后将剩下的一组用做测试集。

举例子：将源数据切分为了1、2、3三个数据集

• 第一次：数据集1，2作为训练集，3作为测试集
• 第二次：数据集1，3作为训练集，3作为测试集
• 第三次：数据集2，3作为训练集，3作为测试集
  最后求均值

from sklearn.cross_validation import train_test_split
# sklearn.cross_validation是交叉验证模块，train_test_split对原始数据集进行切分
# 整个原始数据集，test_size=0.3表示把30%的数据作为测试集
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3, random_state = 0)
print("Number transactions train dataset: ", len(X_train))
print("Number transactions test dataset: ", len(X_test))
print("Total number of transactions: ", len(X_train)+len(X_test))
# 下采样的数据
X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample ,y_undersample ,test_size = 0. ,random_state = 0)
print("")
print("Number transactions train dataset: ", len(X_train_undersample))
print("Number transactions test dataset: ", len(X_test_undersample))
print("Total number of transactions: ", len(X_train_undersample)+len(X_test_undersample))

输出：

Number transactions train dataset:  199364
Number transactions test dataset:  85443
Total number of transactions:  284807

Number transactions train dataset:  688
Number transactions test dataset:  296
Total number of transactions:  984

4、模型评估方法

假设有1000个病人的数据,要对1000个病人进行分类,有哪些是癌症的?哪些不是患有癌症的?假设其中有990个人不患癌症,10个人是患癌症。
（1）将1000个样本输入到模型中，精度=990/1000=99%
（2）召回率recall：表示根据目标制定衡量的标准，在一个只有10人的样本里，查到2个人患癌症，那召回率为0.2

5、正则化惩罚

比如有两个训练模型，A模型：ø1、ø2、ø3…ø10，B模型：ø1、ø2、ø3…ø10，这两个模型的recall值都是等于90%。A模型的原点浮动比较大,呈波浪形，B模型的原点浮动比较小。
一般都希望得到B模型这样的，之后在测试集上训练使得过度拟合（过度拟合的意思是在训练集表达效果很好，但是在测试集表达效果很差）的风险更小。从而引入正则化，惩罚模型的ø，大力度惩罚A模型，小力度惩罚B模型。
（1）L2正则化
惩罚：损失函数+1/2w*w
对于A模型，w值浮动大，计算出来的值就大
（2）L1正则化
惩罚：损失函数+|w|

可以设置当前惩罚力度有多大，比如0.1倍的L2正则化

#Recall = TP/(TP+FN)
from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report 
# 这里的KFold是指交叉验证的时候,可以选择做几倍的交叉验证; cross_val_score值是指交叉验证评估得到的结果
def printing_Kfold_scores(x_train_data,y_train_data):
    # 将数据集切分为5份
    fold = KFold(len(y_train_data),5,shuffle=False)
    # 正则惩罚力度
    c_param_range = [0.01, 0.1, 1, 10, 100]
    
    results_table = pd.DataFrame(index = range(len(c_param_range),2), columns = ['C_parameter','Mean recall score'])
    results_table['C_parameter'] = c_param_range
    
    j=0
    # 找到最好的一个c参数
    for c_param in c_param_range:
        print('-------------------------------------------')
        print('C parameter: ', c_param)
        print('-------------------------------------------')
        print('')
        
        recall_accs = []
        for iteration, indices in enumerate(fold,start=1):
            # 传入C这个惩罚力度，方式可选l1或则l2
            lr = LogisticRegression(C=c_param,penalty = 'l1')
            # 对模型进行训练
            lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
            # 预测
            y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)
            
            recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
            recall_accs.append(recall_acc)
            print('Iteration', iteration,': recall score = ',recall_acc)
        results_table.ix[j,'Mean recall score']=np.mean(recall_accs)
        j += 1
        print('')
        print('Mean recall score ', np.mean(recall_accs))
        print('')

    best_c = results_table.loc[results_table['Mean recall score'].idxmax()]['C_parameter']
    
    # Finally, we can check which C parameter is the best amongst the chosen.
    print('*********************************************************************************')
    print('Best model to choose from cross validation is with C parameter = ', best_c)
    print('*********************************************************************************')
    
    return best_c

best_c = printing_Kfold_scores(X_train_undersample,y_train_undersample)

-------------------------------------------
C parameter:  0.01
-------------------------------------------

Iteration 1 : recall score =  0.958904109589
Iteration 2 : recall score =  0.931506849315
Iteration 3 : recall score =  1.0
Iteration 4 : recall score =  0.972972972973
Iteration 5 : recall score =  0.954545454545

Mean recall score  0.963585877285

-------------------------------------------
C parameter:  0.1
-------------------------------------------

Iteration 1 : recall score =  0.835616438356
Iteration 2 : recall score =  0.86301369863
Iteration 3 : recall score =  0.966101694915
Iteration 4 : recall score =  0.945945945946
Iteration 5 : recall score =  0.909090909091

Mean recall score  0.903953737388

-------------------------------------------
C parameter:  1
-------------------------------------------

Iteration 1 : recall score =  0.849315068493
Iteration 2 : recall score =  0.86301369863
Iteration 3 : recall score =  0.983050847458
Iteration 4 : recall score =  0.945945945946
Iteration 5 : recall score =  0.909090909091

Mean recall score  0.910083293924

-------------------------------------------
C parameter:  10
-------------------------------------------

Iteration 1 : recall score =  0.86301369863
Iteration 2 : recall score =  0.890410958904
Iteration 3 : recall score =  0.983050847458
Iteration 4 : recall score =  0.945945945946
Iteration 5 : recall score =  0.924242424242

Mean recall score  0.921332775036

-------------------------------------------
C parameter:  100
-------------------------------------------

Iteration 1 : recall score =  0.86301369863

通过结果可以看出,当惩罚参数是0.01,recall的值最高.

6、混淆矩阵

混淆矩阵是由一个坐标系组成的,有x轴以及y轴,在x轴里面有0和1,在y轴里面有0和1.x轴表达的是预测的值,y轴表达的是真实的值。

def plot_confusion_matrix(cm, classes,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
#     plt.yticks(tick_marks, classes)
    
    thresh = cm.max() / 2.
    for i,j in itertools.product(range(cm.shape[0]),range(cm.shape[1])):
        plt.text(j,i,cm[i,j],
                 horizontalalignment="center",
                 color="white" if cm[i, j]>thresh else "black")
    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')


import itertools
lr = LogisticRegression(C = best_c,penalty = 'l1')
lr.fit(X_train_undersample, y_train_undersample.values.ravel())
y_pred_undersample = lr.predict(X_test_undersample.values)

# 计算混淆矩阵
cnf_matrix = confusion_matrix(y_test_undersample,y_pred_undersample)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset:", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# 画图
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix,
                      classes=class_names,
                      title='Confusion matrix')
plt.show()

输出结果：

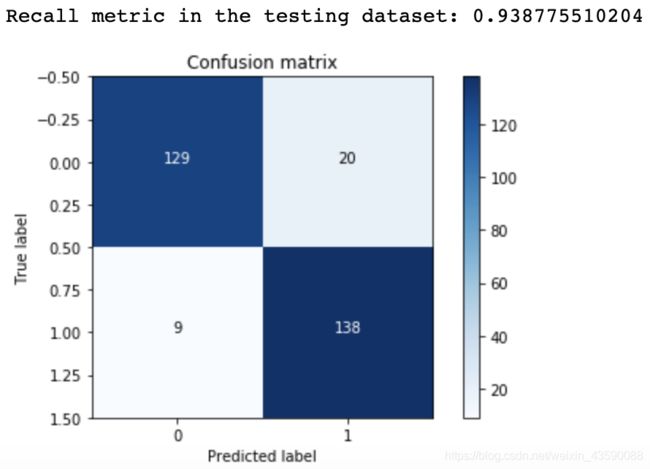
真实为1，预测为1，得到结果是137；真实为1，预测为0，得到结果是10，计算召回率为recall=138/(138+9)
真实为1，预测为1，得到结果是137；真实为0，预测为0，得到结果是129，计算精度为（129+138）/（129+20+9+138）

以上是在下采样数据集上进行的测试，样本只有200多个，所以还需要在原始数据集上进行操作。

lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred = lr.predict(X_test.values)

# 采用原始数据集
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# 画图
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()

输出：

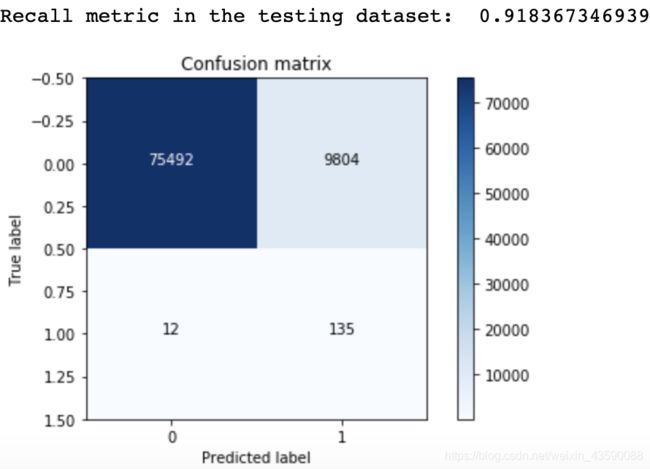
由图可知，召回率的值变化不大，能够达到标准，但是精度值变化很大，找出的9804个无辜样本很影响精度值。

7、逻辑回归阈值对于结果的影响

自定义阈值，研究不同阈值对结果的影响。

lr = LogisticRegression(C = 0.01, penalty='l1')
lr.fit(X_train_undersample, y_train_undersample.values.ravel())
y_pred_undersample_proba = lr.predict_proba(X_test_undersample.values)

threshholds = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]

plt.figure(figsize=(10,10))

j=1
for i in threshholds:
    y_test_predictions_high_recall = y_pred_undersample_proba[:,1] > i
    plt.subplot(3,3,j)
    j+=1
    #计算混淆矩阵
    cnf_matrix = confusion_matrix(y_test_undersample,y_test_predictions_high_recall)
    np.set_printoptions(precision=2)
    print("Recall metric in the testing dataset:", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
    class_names = [0,1]
    plot_confusion_matrix(cnf_matrix
                         ,classes=class_names
                         ,title='Threshhold>=%s'%i)

结果如下：


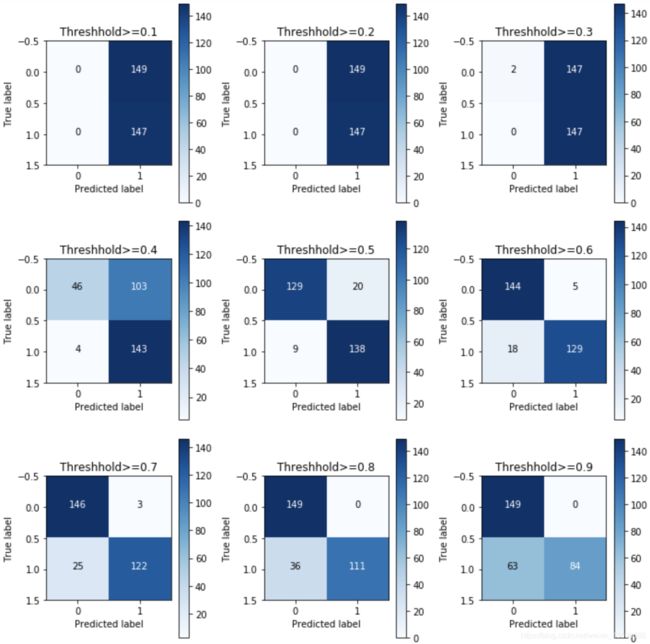
由图可见，阈值越大，误杀值越小，精度变高，但是召回率变小。

8、SMOTE算法

以上操作都是下采样，主要用于模型回归的评估以及参数的选择，下面主要介绍过采样，比如是将100个样本扩展为500个样本。
（1）SMOTE算法

举例：要将一个样本变为5个样本，首先计算它与相邻的5个样本之间的距离，于是新值等于原始值加上距离乘以随机数。
（2）代码实现
需要安装imblearn这个包，遇到问题，在当前的channels中找不到这个包，解决方案http://wenda.chinahadoop.cn/question/6764

import pandas as pd
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split

credit_cards = pd.read_csv('creditcard.csv')
columns = credit_cards.columns
# 删去class那一列
features_columns = columns.delete(len(columns)-1)
features=credit_cards[features_columns]
labels=credit_cards['Class']

features_train, features_test,labels_train, labels_test = train_test_split(features,
                                                                           labels,
                                                                           test_size=0.2,
                                                                           random_state=0)
# 用SMOTE进行数据生成,首先实例化一个对象,叫oversampler,SMOTE可以不使用参数,但是要使每次生成的数据都是一样的,可以random_state=0.
oversampler = SMOTE(random_state=0)
it_sample(features_train,labels_train)传进来的是训练集的x以及训练集的y
os_features, os_labels = oversampler.fit_sample(features_train,labels_train)
# 这里是计算lable1的有多少个
len(os_labels[os_labels==1])

结果如下：
共有227454个.lable0的也有20多万个,因此样本就均衡了

227454

可以看召回率是多少

os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
best_c = printing_Kfold_scores(os_features,os_labels)

结果如下：

-------------------------------------------
C parameter:  0.01
-------------------------------------------

Iteration 1 : recall score =  0.890322580645
Iteration 2 : recall score =  0.894736842105
Iteration 3 : recall score =  0.968861347792
Iteration 4 : recall score =  0.957111924468
Iteration 5 : recall score =  0.958419889867

Mean recall score  0.933890516976

-------------------------------------------
C parameter:  0.1
-------------------------------------------
Iteration 1 : recall score =  0.890322580645
Iteration 2 : recall score =  0.894736842105
Iteration 3 : recall score =  0.970410534469
Iteration 4 : recall score =  0.960156516196
Iteration 5 : recall score =  0.959178289973

Mean recall score  0.934960952678

-------------------------------------------
C parameter:  1
-------------------------------------------

Iteration 1 : recall score =  0.890322580645
Iteration 2 : recall score =  0.894736842105
Iteration 3 : recall score =  0.970543321899
Iteration 4 : recall score =  0.960321385784
Iteration 5 : recall score =  0.960541211901

Mean recall score  0.935293068467

-------------------------------------------
C parameter:  10
-------------------------------------------

Iteration 1 : recall score =  0.890322580645
Iteration 2 : recall score =  0.894736842105
Iteration 3 : recall score =  0.970432665708
Iteration 4 : recall score =  0.959628933514
Iteration 5 : recall score =  0.960815994548

Mean recall score  0.935187403304

-------------------------------------------
C parameter:  100
-------------------------------------------

Iteration 1 : recall score =  0.890322580645
Iteration 2 : recall score =  0.894736842105
Iteration 3 : recall score =  0.970499059422
Iteration 4 : recall score =  0.960321385784
Iteration 5 : recall score =  0.95657335048

Mean recall score  0.934490643687

*********************************************************************************
Best model to choose from cross validation is with C parameter =  1.0
*********************************************************************************

通过以上的结果可以知道recall值平均算下来大概是0.934

混淆矩阵

lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(os_features,os_labels.values.ravel())
y_pred = lr.predict(features_test.values)

# Compute confusion matrix
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)

print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))

# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=class_names
                      , title='Confusion matrix')
plt.show()

结果：

由图可知，误杀值为517，比使用下采样的误杀值少很多，精度提高，但是召回率偏低。

总结：对于样本不均衡数据,要利用越多的数据越好，下采样误杀率很高,这是模型本身自带的一个问题。因为0和1一样少,会存在潜在的意识是原始数据0和1的数据一样少,导致误杀率偏高.过采样的结果偏好一些,虽然recall偏低了一点,但是整体的效果还是不错的。

参考：https://www.jianshu.com/p/ad394fecedbf