算法设计与分析 实验三 回溯法求解地图填色问题

一、实验目的与要求

1、实验基本要求：

（1）掌握回溯法算法设计思想。
（2）掌握地图填色问题的回溯法解法。

2、实验亮点：

（1）通过回溯法完成了实验，并验证了结果的正确性。
（2）在使用回溯法的基础上，从贪心剪枝，置换剪枝，向前探查剪枝，矩阵记录和选择邻接表进行数据存储5个方面对程序进行优化，大幅降低程序运行时间并在附件中上传了所有实验过程中的输出结果并对结果都进行了验证。
（3）通过实际操作与理论分析结合的方式，从图规模，合法涂色数，图的边密度和图的连通分量四个方面分析对比算法的效率。
（4）有针对性地探究了找到全部可行解的方法。
（5）最后思考并探究了轮换等有效剪枝策略，极大提高算法效率。

二、实验内容与方法

背景知识：
为地图或其他由不同区域组成的图形着色时，相邻国家/地区不能使用相同的颜色。 我们可能还想使用尽可能少的不同颜色进行填涂。一些简单的“地图”（例如棋盘）仅需要两种颜色（黑白），但是大多数复杂的地图需要更多颜色。
每张地图包含四个相互连接的国家时，它们至少需要四种颜色。1852年，植物学专业的学生弗朗西斯·古思里（Francis Guthrie）于1852年首次提出“四色问题”。他观察到四种颜色似乎足以满足他尝试的任何地图填色问题，但他无法找到适用于所有地图的证明。这个问题被称为四色问题。长期以来，数学家无法证明四种颜色就够了，或者无法找到需要四种以上颜色的地图。直到1976年德国数学家沃尔夫冈·哈肯（Wolfgang Haken）（生于1928年）和肯尼斯·阿佩尔（Kenneth Appel，1932年-2013年）使用计算机证明了四色定理，他们将无数种可能的地图缩减为1936种特殊情况，每种情况都由一台计算机进行了总计超过1000个小时的检查。
他们因此工作获得了美国数学学会富尔克森奖。在1990年，哈肯（Haken）成为伊利诺伊大学（University of Illinois）高级研究中心的成员，他现在是该大学的名誉教授。
四色定理是第一个使用计算机证明的著名数学定理，此后变得越来越普遍，争议也越来越小 更快的计算机和更高效的算法意味着今天您可以在几个小时内在笔记本电脑上证明四种颜色定理。

问题描述：
我们可以将地图转换为平面图，每个地区变成一个节点，相邻地区用边连接，我们要为这个图形的顶点着色，并且两个顶点通过边连接时必须具有不同的颜色。附件是给出的地图数据，请针对三个地图数据尝试分别使用5个（le450_5a），15个（le450_15b），25个（le450_25a）颜色为地图着色。

三、实验步骤与过程

1、未优化的回溯：

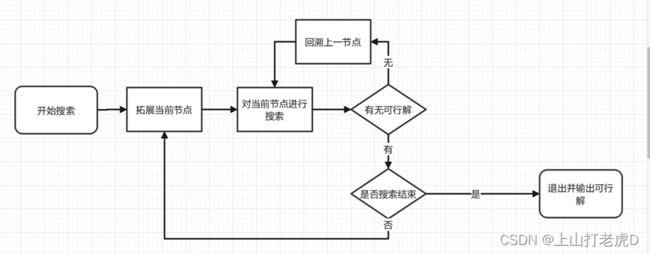
（1）算法描述：

a. 拓展当前节点，并对当前节点进行搜索
b. 判断当前节点是否存在可行解，如果存在则进入c，如果不存在，则回溯上一节点，并进入a
c. 判断是否搜索结束，如果结束则直接输出结果并停止搜索；如果未结束，则进入a
d. 当全部搜索完毕后仍不存在可行解，则输出无解

未经过优化的回溯算法流程图大致如下

（2）编程实现

大致代码如下：

void dfs(int x) {
    //如果已经涂完整个地图，即找到可行解
    if (x > n) {
        ans++;
        return;
    }
    //对每个点进行涂色
    for (int i = 1; i <= m; i++) {
        color[x] = i;//模拟涂色
        //进行涂色的合法性检测
        for (int j = 1; j <= x; j++) {
            if (g[j][x] && color[j] == color[x]) {
                b = 1;
                break;//非法，重新染色
            }
        }
        if (b) {
            b = 0;
        } else {
            dfs(x + 1);//当前解合法，对当前节点进行拓展搜索
        }
    }
}

（3）运行并测试：

为了对算法进行测试，我选择了实验时给定的如下地图数据，并进行填涂尝试。

①图像数据文字化：
由于对于代码而言，不能够存储图像，因此需要将图像数据转为邻接矩阵进行图的存储。

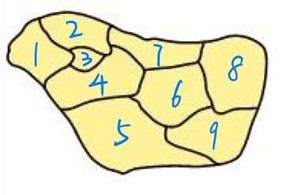
将每个小块看成图的一个点，将图与图之间的邻接关系映射成点与点之间的连边。

②进行小数据试涂：
采用输入流将每个连边读入后调用函数进行计算，并通过输出流将结果输出（全部运行结果在‘result’->‘9_4_480.txt’中）并利用系统函数进行计时，可得对于这个给定地图，未优化的回溯在0.8544ms下找到全部480个解。

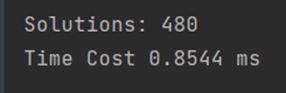
③涂色正确性检验：
完成了对地图的涂色后，务必对算法进行正确性检验以证明我们的涂色方案是正确的。

易知，涂色的正确性检验即检测所填涂地图中相邻的边的涂色是否相同，如果相同则为非法涂色，如果所有相邻点涂色都不同则涂色合法。

检测方法也相对简单，仅需遍历整个边集，并依次对相邻点进行颜色检验即可。通过检验，②中试涂的480个结果全部正确。证明回溯算法具有正确性。
④大数据试涂：
完成了小数据下的试涂后，尝试对大数据进行涂色，不过发现对附件中450点使用5色填涂不能在短时间内运行结束，并且运行比较长一段时间（12h+）也很难得到结果。这说明，常规的回溯算法只适用于数量级较小的数据，回溯算法亟待优化。

2、对回溯进行优化（本部分中时间消耗均为完备搜索的时间消耗）：

从上面的实验中，我们可以知道，常规的回溯算法耗时很长，而且搜索效率较慢，只能处理较低数量级的数据。因此需要对算法进行一系列优化。通过对运算过程的分析与计算，提出了如下几种可行的优化方案：（每种优化方案均进行了测试，并将测试结果存在‘result’文件夹中）

（1）贪心剪枝策略：

①算法描述：
通过分析，我们不难发现，对于搜索过程中产生的搜索树最大深度一定，但分支数很大，因此需要采用策略去降低搜索树的分支个数，从而对搜索树进行剪枝。
通过分析，我们可以知道，对于每次搜索出的节点，拓展的节点为当前的可行解个数。而且，分支产生的越早，分支就会产生的越多。因此，需要降低搜索树树根处分支数，尽量将分支数靠近叶子节点，从而进行贪心剪枝。

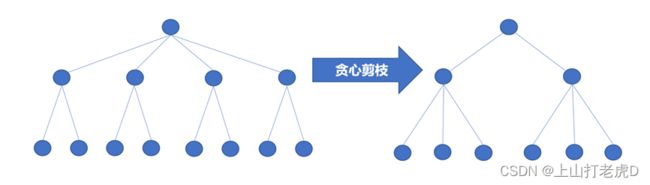
通过分析可以得知，不论从哪个点开始搜索，得到的可行解不变。因此，只需从度数大的点开始搜起，并依次按照点度数降序顺序依次搜索，直至搜索到最后一个点即可。

②具体实现：
本算法的具体实现相对简单，只需在最开始读入图数据之后，进行搜索之前按照点度数降序排序对图进行重构，再进行搜索即可。

//比较点度数函数
bool comp(const MapNode tmp1, const MapNode tmp2) {
    return tmp1.value < tmp2.value;
}
//排序重构函数
void arraySort() {

        sort(vArray + 1, vArray + vNum + 1, comp);
        for (int i = 1; i <= vNum; i++) {
            oldToNew[vArray[i].id] = i;
            newToOld[i] = vArray[i].id;
        }
    }

③运行并测试：
对给定的大数据（450点5色）进行填涂，并将可行解全部输出，将程序运行20次取时间平均值做表如下：

优化前	优化后
449.4s	109.4s

这证明，使用贪心算法进行优化是切实有效的优化方式，但算法的运行时间仍然比较长，需要进一步优化。

（2）置换剪枝策略：

①算法描述：
通过观察第一次优化输出的可行解，我们不难发现，在起始搜索点的不同涂色方案下的可行解个数相同，这是因为对于第一个搜索点而言，不同涂色下的各个填涂方案是对称的。即对于在涂色$x_0$下的解向量$S_0=(x_0,x_1,x_2,x_3,\dots )$，可以映射出$n-1$（n为可用颜色数）个等效可行解。因此搜索时只需固定第一个点，并将搜索出来的可行解个数乘以可用颜色数即可。大约可以将实际运行时间缩短至原来的$\frac{1}{n}$（$n$为可用颜色数）。
②具体实现：
本算法的具体实现很简单，只需在搜索时固定第一个颜色即可

③运行并测试：
对给定的大数据（450点5色）进行填涂，并将可行解全部输出，将程序运行20次取时间平均值做表如下：

优化前	优化后
679s	140.4s

这证明，使用置换剪枝策略进行优化是切实有效的优化方式，但算法的运行时间仍然比较长，需要进一步优化。

（3）向前探查剪枝策略：

①算法描述：
在搜索过程中，对于一些无解的节点，可以做到提前探查，即拓展节点前先对是否存在可行解进行检查，如果不存在可行解，则剪枝并返回。

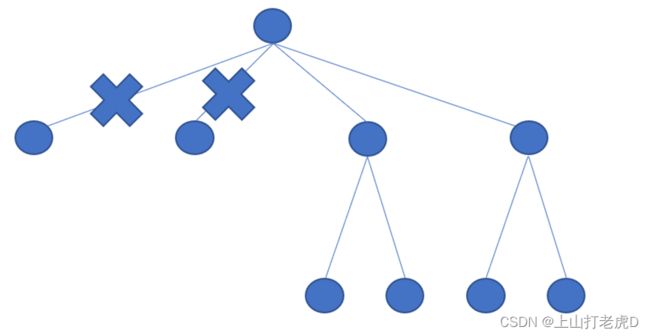
②具体实现：
在本题中，采用了colorMatrix数组对每个点可以使用的颜色进行计数。并在回溯搜索时对当前点的合法颜色进行检测，如果没有则直接返回，无需拓展。

③运行并测试：
对给定的大数据（450点5色）进行填涂，并将可行解全部输出，将程序运行20次取时间平均值做表如下：

优化前	优化后
264.1s	249.5s

这证明，使用向前探查剪枝策略进行优化是有效的优化方式，但优化并不十分明显。

（4）矩阵记录可行解避免多次搜索

①算法描述：
在进行回溯搜索过程中，每次对点进行颜色合法性检查时都要遍历当前点，每一次每一层的搜索都需要检查合法性，成千上万次操作将大大提高这部分的时间消耗。而每次拓展节点时，新节点与原节点都会有公共边，因而点的可用性不会差别特别大，因此，可以设计一个数组对每个点的可用性进行检测并存储，从而避免多次对可用性的检测。

②具体实现：
为了存储每个点的颜色可用性，设置了colorMatrix进行存储。其中，colorMatrix[i][1]表示第i点1颜色是否可用（可用为1，反之为0），colorMatrix[j][2]表示第j点2颜色是否可用（可用为1，反之为0）。特殊地，colorMatrix[i][0]表示第i点共有几种可用颜色
因此对于每个点回溯时，只需通过colorMatrix遍历点i的可用颜色，再删除邻接点colorMatrix可用颜色并继续搜索即可。完成搜索则恢复该可用颜色即可。

a.搜索函数：

//backtrack to search
void backtrack(Map &map, int index, int rest) {
    //judge if find the solution
    if (rest == 0) {
        //store the solution
        result.push_back(vector<int>(map.colorArray + 1, map.colorArray + 1 + map.vNum));
        for (int i = 0; i < map.vNum; i++) {
            ofs << result[result.size() - 1][i];
        }
        ofs << endl;
        return;
    }
    //dissatisfied solution: check each valid color
    for (int i = 0; i < map.colorType; i++) {
        if (map.colorMatrix[index][i + 1] == 0) {
            //if the color solution is invalid
            if (deleteColor(map, index, i) != -1) {
                recoverColor(map, index, i);
                continue;
            }
            //search point[index]
            map.colorArray[index] = i;
            //backtrack to search
            backtrack(map, next(map), rest - 1);
            //recover the validation of the color and return
            map.colorArray[index] = -1;
            recoverColor(map, index, i);
        }
    }
    return;
}

首先回溯函数中对是否为解进行判断，如果是解，则将结果存入结果容器中，并直接返回。
如果当前不为可行解，且当前点没有合法可用颜色，则进入下一个点的判断。如果有可用颜色，则对当前节点的可用颜色进行拓展，并使用colorMatrix对颜色情况进行记录，搜索前删除该可用颜色，搜索后恢复该可用颜色。

b.恢复颜色函数：

void recoverColor(Map &map, int index, int color) {
    MapNode candidate = map.vArray[index];
    MapNode *tmp = candidate.next;
    while (tmp) {
        int candidateIndex = tmp->value;
        //if the point is uncolored and its adjacent point is not colored with that color
        if (map.colorArray[candidateIndex] == -1 && map.colorMatrix[candidateIndex][color + 1] == 1 + index) {
            map.colorMatrix[candidateIndex][color + 1] = 0;
            if (map.colorMatrix[candidateIndex][0] == 0) {
                map.colorMatrix[candidateIndex][0]++;
                return;
            }
            map.colorMatrix[candidateIndex][0]++;
        }
        tmp = tmp->next;
    }
}

对于每个搜索的点，当他下一个邻接点不为空时，则进行搜索。首先判断当该点未涂色且该点邻接点颜色合法时，则可以认为该点的当前涂色合法，将colorMatrix对应值加一并返回即可。

c.删除颜色函数：

int deleteColor(Map &map, int index, int color) {
    MapNode candidate = map.vArray[index];
    MapNode *tmp = candidate.next;
    while (tmp) {
        int candidateIndex = tmp->value;
        //if the point is uncolored and its adjacent point is not colored with that color
        if (map.colorArray[candidateIndex] == -1 && map.colorMatrix[candidateIndex][color + 1] == 0) {
            map.colorMatrix[candidateIndex][color + 1] = 1 + index;
            map.colorMatrix[candidateIndex][0]--;
            if (map.colorMatrix[candidateIndex][0] == 0)
                return candidateIndex;
        }

        tmp = tmp->next;
    }
    return -1;
}

对于每个搜索点，如果该点的下一个邻接点的可涂色颜色为0，则返回当前点的序号，如果不存在下一个邻接点，则返回-1。对于邻接点可涂颜色不为0的情况，则更新邻接点可涂颜色直至搜索到末端点。

（5）数据结构的选择：

①算法描述：
对于储存图的数据结构，常见的有邻接表和邻接矩阵两种。因此如何选择合适的数据结构也将从一定程度上节省程序的运行时间。

对于邻接矩阵，寻找相邻区域时需要遍历所有区域；对于邻接表而言，可以直接获取相邻区域。由于本地搜索程序与深度优先搜索类似，而采用邻接表的深度优先搜索的时间复杂度为$O(n+e)(e为边数)$，采用邻接矩阵的深度优先搜索的时间复杂度为$O(n^2)$。因此在搜索时，可以采用邻接表进行搜索。但对于邻接表而言，对于一些数据的存储没有邻接矩阵方便，因此可以采用邻接矩阵和邻接表共用的方式对图结构进行存储。
②具体实现：

struct Map {
    int vNum;          //number of vertex
    MapNode *vArray;   //adjacency list
    int *colorArray;   //store type of color, -1 for uncolored
    int colorType;     //type of color
    int *oldToNew;     //change after sort by degree, origin id-> new id
    int *newToOld;     //change after sort by degree, new id-> origin id
    bool **matrix;     //adjacency matrix
    int **colorMatrix; //store the validation of each point and number of valid colors
};

使用colorMatrix二维矩阵存储各个点的颜色可用情况，使用vArry存储邻接表，使用colorArray存储点的涂色情况。

③运行并测试：
对给定的大数据（450点5色）进行填涂，并将可行解全部输出，将程序运行20次取时间平均值做表如下：

优化前	优化后
240.5s	169.4s

这证明，使用邻接表存储数据并进行优化是有效的优化方式。

3、时间与效率分析：

利用以上算法优化，完成不同规模下数据的试涂色记录并整理如下（搜索结果在‘result’文件夹中）：

（1）三组数据的涂色：

①得到第一个可行解：

	450点5色	450点15色	450点25色
时间消耗	860.1ms	386.4ms	210.6ms

可以看到随着可用颜色的增多，涂色消耗时间依次缩短。这是由于可用颜色更多，搜索过程中更容易搜索到可行解，无需进行多次搜索就可以找到可行解。

②得到全部可行解（15色和25色全部可行解个数超过10^9无法一定时间内得到完备搜索结果）：

	450点5色
时间消耗	61.199s
可行解个数	3840

可以看到采用贪心剪枝，置换剪枝，向前探查剪枝，矩阵记录并选择邻接表进行数据存储这5种优化后，实现了从最开始未优化时短时间内无法完成完备搜索变为在一分钟左右的时间即可完成全部搜索，算法的效率得到极大提升。

（2）自行生成地图涂色并分析：

通过随机数，自行生成了不同规格的地图，对于每个地图，均将程序运行10次并取平均值作为实际值。对于每次比较时，均需要保证其余变量的值不变，在有解的情况下，分析统计作表如下：

①图规模对运行时间的影响：

	100点5色	200点5色	300点5色	400点5色
时间消耗	1,943ms	10,673ms	24,164ms	60,561ms

图的规模极大影响了搜索的规模，规模小的图要比规模大的图的搜索时间小的多。
通过上图，可以看到，当地图规模成线性级增长时，时间消耗大致成指数型增长。并且，随着数量级的增长，指数增长速率放缓，这是因为多种剪枝策略对大数据下优化作用更明显。

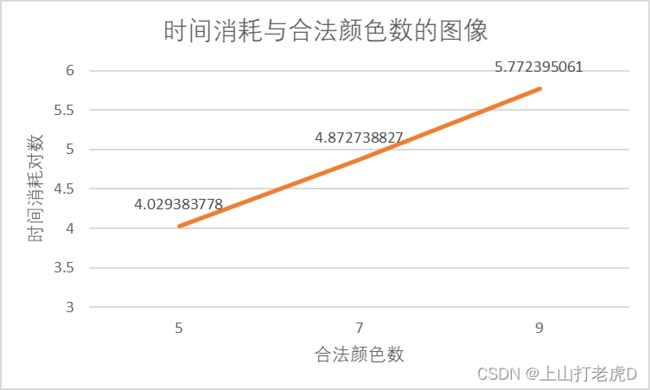
②合法涂色数对运行时间的影响：

	200点5色	200点7色	200点9色
时间消耗	10.7s	74.6s	592.1s

合法的颜色数极大的影响了搜索的规模，合法颜色少的图要比合法颜色多的图的搜索时间小的多。
通过分析可知，若对于某图涂色的存在可行解向量$S_0=(x_0,x_1,x_0,x_0,\dots )$则$S_1=(x_1,x_0,x_1,x_1,\dots )(交换x_0,x_1)$则存在$n!$种等效可行解向量。因此，当合法颜色数增多时，可行解数量大致成阶乘型（指数）增加。
此外，随着合法颜色数的增长，指数增长速率增大，这是因为由于合法颜色数的增加导致可剪枝数降低，搜索树成指数级增长，剪枝策略的优化作用减弱。

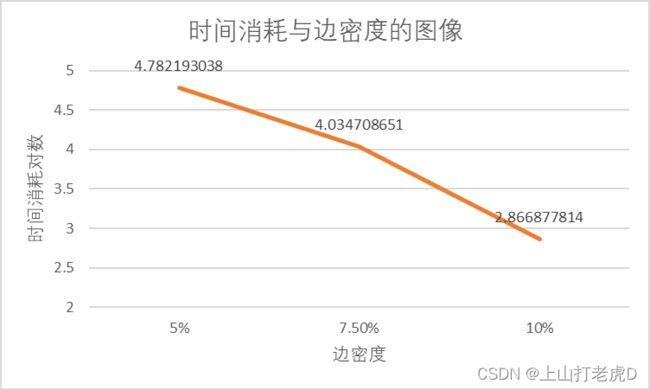
③图的边密度对运行时间的影响（在400点5色下进行测试）：

	边密度5%	边密度7.5%	边密度10%
时间消耗	60,561ms	10,832ms	736ms

边密度影响了可行解的个数，也影响了剪枝的效率。边密度越大，剪枝效率越高。边密度越小，搜索树的每一支就会更深。
从上图以及上表中可以看出，随着边密度的提高，时间消耗指数级急速降低。这是剪枝效率大大提升的原因。

④图的连通分量对运行时间的影响（在400点5色下进行测试）：

联通分量	1	3	5
时间消耗	60,561ms	54,831ms	48,265ms

联通分量从一定程度上影响了搜索树的规模。当搜索过程中搜索完一个极大连通图后，搜素会从下一个极大连通图的最大度节点开始搜索，而不是从原节点上继续拓展，类似于重新从根节点伸展出一颗新的搜索树，降低了上一级的节点拓展。从一定程度上节省了时间。
通过分析上图以及上表，可以看到连通分量确实对图的运行时间有影响，并且连通分量越大，算法运行时间越短。

四、实验结论或体会

1. 常规算法的算法效率往往较低，需要进行优化
2. 对于回溯搜索算法，搜索时应优先选择限制较多的分支进行拓展搜索
3. 可以通过数学方法对算法进行优化。例如本实验中借助图论中轮换的思想完成了优化。
4. 除了算法本身，选择合适的数据结构也可以在一定程度上降低程序的运行时间。
5. 算法优化过程中，算法的正确性验证必不可少。在本题中，每种优化策略都经过了理论和实际进行验证。

五、思考

轮换替换思想的推广：

1、算法描述：

通过对运行结果中可行解的分析以及对涂色逻辑的分析我们可以知道，对于m个合法颜色，规模为n的图的一个解向量如果为$$S_0=(c_0,c_1,c_0,c_2\dots )(c_0,c_1,c_2\dots 互异颜色)$$，则$$S_1=(c_1,c_0,c_1,c_2\dots ),S_2=(c_1,c_2,c_1,c_0\dots )\dots$$也都为可行解。
即对于已经找到的可行解，可以通过轮换获得更多可行解。由于颜色之间满足互异性原则，且解向量中的颜色满足全排列性质。因此确定一个可行解，可映射出$A_n^n=n!$个可行解。通过这个规律可以在短时间内获取巨大数量级的可行解。对于5色，找到一个可行解等于找到$A_5^5=5!=120$个可行解；对于$15$色，找到一个可行解等于找到$A_1{5}^{1}5=15!=1,307,674,368,000$个可行解；对于$25$色，找到一个可行解等于找到$A_2{5}^{2}5=25!=15,511,210,043,330,985,984,000,000$个可行解。
此外，对于不可行的搜索节点也同理，当找到搜索树的某一枝无解后，可以利用轮换，将所有等效解全部剪枝剪掉，这大大降低了程序的运行时间。

2、运行并测试：

采用轮换进行剪枝的策略和上面几种已经介绍的剪枝策略，对450点5色地图进行涂色并计时，发现仅需要不到一秒的时间即可完成全部3840个点的搜索，与之前大约一分钟左右的时间相比，算法效率得到极大提升。

附录：

除以上尝试外，我还进行了一些其他的尝试，经过若干种算法的优化，最终可以在$60ms$内搜出3840个全部可行解，将具体代码附上如下：

#include 
#include 

using namespace std;

#define COLOR 5    //颜色数
#define VERTEX 90     //点数
#define EDGE 500   //边数

class Vertex {
public:
    int color;
    int state[COLOR + 1];  //颜色状态，1为可选，非1为不可选
    int choice;  //可选颜色数，即state中1的数量
    int restrain;  //相邻数量
    Vertex() {
        color = 0;
        for (int i = 0; i < COLOR + 1; ++i) {
            state[i] = 1;
        }
        choice = COLOR;
        restrain = 0;
    }
};


//int map[VERTEX + 1][VERTEX + 1];  //图的邻接矩阵
int map2[VERTEX + 1][256];  //图的邻接表
long long int sum = 0;   //记录解的个数
long Start;
long End;


int ColorFirst(Vertex *S) {
    int maxRestrain = 0, maxIndex = 0;
    for (int i = 1; i <= VERTEX; ++i) {
        if (S[i].restrain > maxRestrain) {
            maxRestrain = S[i].restrain;
            maxIndex = i;
        }
    }
    S[maxIndex].color = 1;
    maxRestrain = 0;
    int next = 0;
    for (int k = 1; k <= map2[maxIndex][0]; ++k) {
        int j = map2[maxIndex][k];
        S[j].choice--;
        S[j].restrain--;
        S[j].state[1] = -maxIndex;
        if (S[j].restrain > maxRestrain) {
            maxRestrain = S[j].restrain;
            next = j;
        }
    }
    return next;
}

int getNext(Vertex *S) {
    int min = COLOR;
    int next = 0;
    for (int i = 1; i <= VERTEX; ++i) {
        if (S[i].color == 0) {
            if (S[i].choice == min) {
                if (S[i].restrain > S[next].restrain) {
                    min = S[i].choice;
                    next = i;
                }
            } else if (S[i].choice < min) {
                min = S[i].choice;
                next = i;
            }
        }
    }
    return next;
}

//搜索函数
int DFS(Vertex *S, int now, int count, int used) {
    if (count == VERTEX) //到达叶子,找到一个着色方案
    {
        /*End = clock();
        cout << End - Start << endl;
        for (int i = 1; i <= VERTEX; i++) //输出该着色方案
            cout << S[i].color << " ";
        cout << endl;
        exit(1);*/

        sum += S[now].choice;

        /*if (sum > 1000000000) {
            End = clock();
            cout << End - Start << endl;
            exit(1);
        }*/

        return S[now].choice;

    } else {
        int s = 0;
        for (int i = 1; i <= COLOR; i++) {
            if (S[now].state[i] == 1) {
                int ss = 0;
                S[now].color = i;
                bool isNew = i > used;
                //剪枝
                for (int k = 1; k <= map2[now][0]; ++k) {
                    int j = map2[now][k];
                    if (S[j].color == 0 && S[j].state[i] == 1) {
                        /*S[j].state[i] = -now;
                        S[j].choice--;
                        S[j].restrain--;*/
                        if (S[j].choice == 1) {
                            goto BACK;
                        } else {
                            S[j].state[i] = -now;
                            S[j].choice--;
                            S[j].restrain++;
                        }
                    }
                }
                if (isNew)
                    ss = DFS(S, getNext(S), count + 1, used + 1);
                else
                    ss = DFS(S, getNext(S), count + 1, used);

                BACK:
                for (int k = 1; k <= map2[now][0]; ++k) {
                    int j = map2[now][k];
                    if (S[j].state[i] == -now) {
                        S[j].choice++;
                        S[j].restrain++;
                        S[j].state[i] = 1;
                    }
                }
                S[now].color = 0;
                if (isNew) {
                    s += ss * (COLOR - used);
                    sum += ss * (COLOR - used - 1);
                    break;
                }
                s += ss;
            }
        }
        if (sum > 100000000) {
            End = clock();
            cout << End - Start << endl;
            exit(1);
        } else
            return s;
    }
}

int main() {
    Vertex S[VERTEX + 1];
    FILE *fp;
    int command;
    cin >> command;
    if (command == 1) {
        if ((fp = fopen("G:\\MapData\\MapR_5_90_500.txt", "r")) == NULL)  //打开文件
        {
            printf("Can not open file!\n");
            exit(1);
        }
    } else if (command == 2) {
        if ((fp = fopen("G:\\MapData\\MapR_5_100_500.txt", "r")) == NULL)  //打开文件
        {
            printf("Can not open file!\n");
            exit(1);
        }
    } else if (command == 3) {
        if ((fp = fopen("G:\\MapData\\MapR_5_110_500.txt", "r")) == NULL)  //打开文件
        {
            printf("Can not open file!\n");
            exit(1);
        }
    } else if (command == 4) {
        if ((fp = fopen("G:\\MapData\\MapR_5_120_500.txt", "r")) == NULL)  //打开文件
        {
            printf("Can not open file!\n");
            exit(1);
        }
    }
    int u, v;
    char ch;
    for (int i = 1; i <= EDGE; i++) {
        fscanf(fp, "%c%d%d\n", &ch, &u, &v);
//        map[u][v] = map[v][u] = 1;
        map2[u][0]++;
        map2[u][map2[u][0]] = v;
        map2[v][0]++;
        map2[v][map2[v][0]] = u;
        S[u].restrain++;
        S[v].restrain++;
    }

    cout << "OK" << endl;
    fclose(fp);
    Start = clock();
    int a = DFS(S, getNext(S), 1, 0);
    End = clock();
    cout << "TIME:" << End - Start << endl;
    cout << "ANSWER:" << a << endl;
    return 0;
}