回溯法求地图填色实验(剪枝)
回溯法求地图填色(剪枝)
文章目录
- 回溯法求地图填色(剪枝)
-
- (一) 问题求解
-
-
- 思维风暴(之前瞎想的,可以跳过)
-
- (二)算法思想:回溯
-
- 伪代码:
- 时间复杂度分析:
- (三)剪枝方向
-
- 1. 下层节点选取
-
- 1) 按邻边个数降序选取
- 2) 搜寻邻边时以分支少优先
- 2.向前探查
-
- 1) 探查1步
- 2) 探查2步
- 3) 探查多步
- 3. 数学等效
-
- 1) 利用完全子图 × 阶乘数
- 2) 利用颜色等效 × 等效数
- 总结
(一) 问题求解
我们可以将地图转换为平面图,每个地区变成一个节点,相邻地区用边连接,我们要为这个图形的顶点着色,并且两个顶点通过边连接时必须具有不同的颜色。
思维风暴(之前瞎想的,可以跳过)
关键: 如何提前探知不可行的解?
- 第一个展开的节点怎么选择?下一层又怎么选择?
- 以邻接关系为标准:
- 以顶点序号0展开:每次选择邻边的节点(DFS) (默认无影响)
- 以邻边个数为标准:
- 以邻边个数最少的展开:由于先前填色产生的约束最少,导致下一层选择的情况会增多,(负优化)
- 以邻边个数最多的展开:由于先前填色产生的约束最多,导致下一层选择的情况会减少(合法性判断),得到优化。
-
如何通过一个节点的填色判断不可行? (结束条件)
设置每个顶点的可能性大小(如填四色就为0,1,2,3,4),每次填色之后就判断周边的节点可能性是否为0,若为0则不可行。
-
展开节点使用什么颜色? 优先已填颜色数量最小的颜色?
由于每次填色均在一个for循环中填色,暂时不能理解是否有效。
-
是否能够通过 可能性大小 而决定下层填色节点的优先级 来提前探测到 结束条件。
- 由于已有第一种遍历方法,且图中节点个数多,填色种类少(4色,15色,25色),单单使用可能性大小的区别度不大。所以不能单纯摈弃第一种方法而以可能性作为下层节点选择的判断,因为单单使用可能性大小的区别度不大。
- 如果兼容第一种方法的话,可以选择在邻边个数相同的情况下,再以可能性大小作为优先级来选择下层节点。
- 如果兼容选择的话,需要以可能性大的优先还是以可能性小的优先?
- 以可能性大的优先:?
- 以可能性小的优先:优先探测可能性为1的点附近是否有该点唯一的颜色,如果有,则剪枝。(比如1号节点填了红色,导致2号节点只有蓝色的可能性,那么我就探测2号节点附近是否有蓝色的节点。)
- 如果兼容选择的话,需要以可能性大的优先还是以可能性小的优先?
- 如果只要求方案总数,而不要求具体方案的话
以四色为例,第一个点就有四种可能。由对称性知,如果第一个节点涂上红色的方案数有x种,那么涂上其他三色中的任意一种也会得到相同的方案数x。即:
总方案数 = 第一个节点的第一种方案数 × 颜色种类数
假如原方法时间为1。那么此方法可以固定变为: 1/颜色种类数 的时间
- 细枝末节 如果相邻节点已有 唯一可能性的颜色 或者 也只剩下唯一的同色可能性
- 可以排除,但是回溯时的恢复需要考虑全面。
- 颜色数量 占比可以吗 ? 比如某种颜色填涂次数超过了全部节点的70%,我就直接pass掉该方案。
- 数据结构存储是否会带来时间的提升,比如是用链表还是用矩阵?(当然两个一起更好了。)
后续才知道的总结:必须通过邻边来选取下层节点,便于后续剪枝!
邻边 --> 好剪枝 --> 大规模肯定用
(二)算法思想:回溯
对一个节点进行填色时,如果颜色合法,则填下一层节点。如果所填颜色非法,则回溯到上一层节点重新填色。直至地图所有节点填色完毕。
伪代码:
void paint ( v , color )
setColor( v , color )
if ( v == num -1) sum++
else
for ( c = 1 to colorNum)
if ( legal(v+1,c) ) //如果颜色合法
paint ( v+1,c) //涂色
deleteColor(v+1,c) //涂完回溯
时间复杂度分析:
由于每层节点涂色时有colorNum种颜色选择,需递归n层节点才能得出解。故时间复杂度:
T ( n ) = O ( c o l o r N u m n ) T(n) = O(colorNum ^n) T(n)=O(colorNumn)
可见时间复杂度为指数级,故涂色大规模地图时不得不需要减少解空间来缩小所需时间。
(三)剪枝方向
1. 下层节点选取
1) 按邻边个数降序选取
策略概述:以邻边个数降序排序所有顶点,从最大度数的顶点开始涂色,下一层节点涂度数次多的节点,直到涂到最少度数的节点。
优点:虽然不按邻边搜寻节点,但是此方法可以在前几步就对地图节点产生了相对最多的约束。无需数学等效,跑小规模的示例地图(9顶点)仅需3ms。
缺点:此方法不适用于顶点个数大的大规模图。涂色失败后为了更改周边邻点往往会向上回溯多层直到邻边节点的涂色层数。如图1所示,数字代表涂色层数,当涂色到第55层节点时,由于判断第58层节点没有可涂颜色了,所以得回退更改28层的颜色。但是为了更改第28层节点的颜色,需要从55层向上回溯,然而每次回溯到其余合法层,仍会换种颜色向下涂色到55层。造成大量时间的浪费。
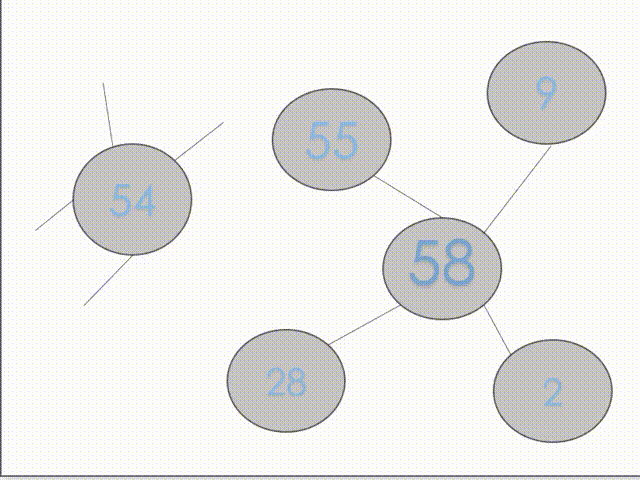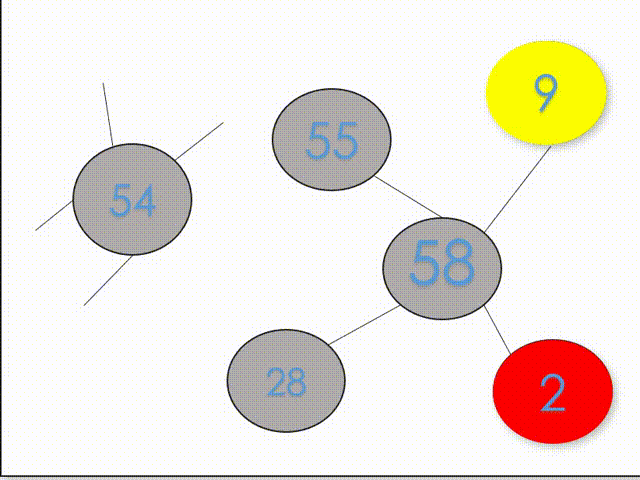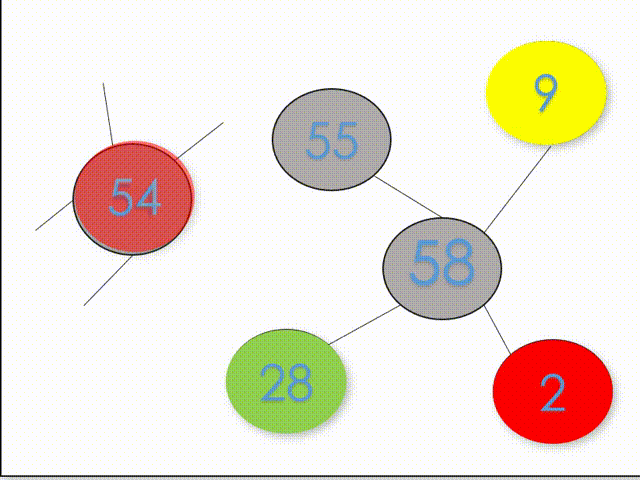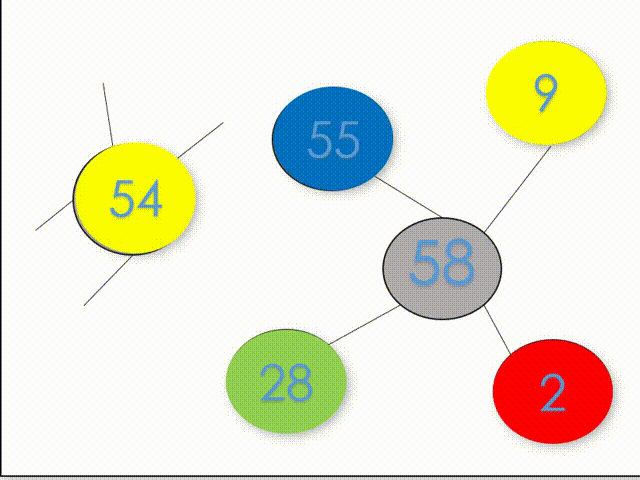
2) 搜寻邻边时以分支少优先
策略概述:优先搜索可涂颜色数最小的节点(MRV),如果可涂颜色相同则优先搜索邻边数量最多的节点(DH)。
优点:容易导致失败的变量先赋值,可以早些发现是否注定失败。如果可涂颜色少的节点注定失败,可以提前回溯,否则会先涂其他颜色的节点后才发现失败。
剪枝节选伪代码:(以插入排序得到最优节点)
//遍历未涂色邻接点存入数组next[num]
void sort(int next[], int num) { //排序next[]数组后得到最优先的节点下标放入next[0]
for (i = 1 to num )
key = next [i]
for (j = i – 1 downTo= 0) {//可能性小的优先 || 邻边小的优先
if ((colorEnableNum[next [j]] > colorEnableNum[key])
|| ((colorEnableNum[next[j]]==colorEnableNum[key])&&(adjoin[next[j]]< adjoin[key]) ) )
next[j + 1] = next[j]//若前面数据较大,则往后移动一位
else
break
next[j + 1] = key //前面数据小于key时,将key插入到数组中。
(可以按此思路改成归并)
2.向前探查
1) 探查1步
如图2所示两种失败情况,通过对点1涂蓝色后,探查周边邻接点是否没可涂色的可能性,或者邻接点是否仅剩蓝色可涂而造成冲突。这样可以提前预知失败而停止回溯。
2) 探查2步
对点1涂黄色后,如果导致周边邻接点2号的可填涂颜色仅剩一种颜色—蓝色,那么可以继续沿着上述思路探查2号邻接点3的可能性。
3) 探查多步
递归通过前两步,可以设计向前探查的递归函数,但实际运行后,发现重复递归探查运行时间无较大改善,甚至导致运行代码增多而导致时间增大。
分析发现递归探查的剪枝可能性小,且容易覆盖第1步探查的剪枝效果导致效率无提升。(排除)
算法真代码:
//填色并减少周边节点可填涂颜色后
bool checkPointIColorJ(int i, int j) {
node *q = list[i]->next;
int k;
while (q != nullptr) { //k 是 点i 的邻接点
k = q->index;
if (colorEnableNum[k] == 0) { //如果k的可填色数为0
// cout << "2";
return false;
} else if (colorEnableNum[k] == 1 && colorP[k][j] == true) { //如果k和i都只能涂同一个色
return false;
} else if (colorEnableNum[k] == 1 ) { //此时k只能填其他色
int w;
int nowColor;
for (w = 0; w < colorType; w++) {
if (colorP[k][w] == true) {
nowColor = w;//仅剩nowColorP色可涂
break;
}
}
node *p = list[k]->next;
while (p != nullptr) { //找到与k相邻接的w
w = p->index;
if (w != i) {
if (colorKind[w] == nowColor) { //如果k的唯一可能颜色已经被填
return false;
}
if (colorEnableNum[w] == 1 && colorP[w][nowColor] == true) { //k 和 w 都只能涂一个色
return false;
}
}
p = p->next;
}
}
q = q->next;
}
return true;
}
3. 数学等效
1) 利用完全子图 × 阶乘数
剪枝概述:由于填涂颜色的对称性,四种颜色之间可以建立一个一一对应的双射关系,,使得颜色轮换后仍满足填色方案。第一个节点四种颜色均等效,第二个节点剩余三种颜色等效…只要找到一个4阶完全子图(在大规模的图中出现概率大),就能实现方案数乘可涂颜色总数的阶乘得到全部方案数。
优点:利用完全n阶子图就能直接乘n!的等效方案数,效率提升显著。
缺点:需要提前找到n阶完全子图。
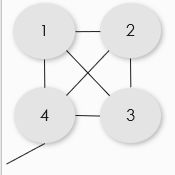
如上图所示,找到4阶完全子图(同时也是4色)即可使用
总方案数 = (4!) × (后续方案数)。
2) 利用颜色等效 × 等效数
剪枝概述:某点填色的时候,如果填到该点 有x种颜色从未被使用过,那么这x种颜色是等效的。如果一条分支中第一次使用 某颜色 ,剩余从未被使用过颜色数为y,就可以找到一种解方案乘y得到所有解。
优点:无需找到完全子图。
缺点:不能直接乘阶乘,仍有部分方案数需要求解,提升的效率较第一种方案低。
算法伪代码:
//准备涂color色
unUseColorNum = getUnUseColorNum()
if (unUseColor[color] == false) //如果color色从未用过
unUseColor[color] = true
sum += paint(v , color) * unUseColorNum
else //用过该色则不使用数学等效
sum += paint(v,color)
总结
- 回溯法的实质是一种蛮力法,通过在解空间遍历所有的解得出结果。而地图填色是一种解空间随颜色或者顶点数增多而指数型增长的问题。使用回溯法的时候就需要通过剪枝来减少解空间。
- 如果找到了colorNum阶完全子图并且仅仅求m种方案数的话,只要colorNum阶乘超过m的话只需求得一解即可(后续解轮换得到)。这或许就是为什么那么多论文算法都只是求1个解而已的原因吧。