python实现knn分类算法和贝叶斯分类算法(数据集为UCI Iris和UCI Bank Marketing)
问题描述:分类算法是解决分类问题的方法,是数据挖掘、机器学习和模式识别中一个重要的研究领域。分类算法通过对已知类别训练集的分析,从中发现分类规则,以此预测新数据的类别。分类算法的应用非常广泛,银行中风险评估、客户类别分类、文本检索和搜索引擎分类、安全领域中的入侵检测以及软件项目中的应用等等。
内容提要:针对教师指定的两类公用数据集(纯数值型例如UCI Iris, 混杂型数据例如UCI Bank Marketing),学生至少实现两种分类算法,并比较分析结果原因。本次实验主要内容包括数据处理、算法实现和评价方法。鼓励与其他方法尤其是业界领先算法进行比较分析,鼓励创新设计求解方法。
实验步骤:
1.读取数据,并做预处理。
2.至少实现两种分类算法,选择评价方法比较结果并分析原因
3.选择适当可视化方法显示结果。
数据集:
UCI Iris:链接:https://pan.baidu.com/s/10T_FWQbHgdTDJtUBMP_wyA
提取码:gk32
UCI Bank Marketing:链接:https://pan.baidu.com/s/1HzEvVeCV5LTiMQmtFzD9jw
提取码:b0p4
一、knn分类算法原理
参考了一篇博客,非常详细,容易理解。
机器学习之knn最邻近分类算法
UCI Bank Marketing数据处理参考文章
1.UCI Iris数据集用knn算法分类
import csv
import random
import math
import operator
import matplotlib.pyplot as plt
#加载鸢尾花数据集 filename(数据存放路径)
def LoadIristdataset(filename):
with open(filename,'rt') as csvfile:
lines=csv.reader(csvfile)
dataset=list(lines)
for x in range(len(dataset)):
for y in range(4):
dataset[x][y]=float(dataset[x][y])
return dataset
#拆分数据集 dataset(要拆分的数据集) split(训练集所占比例) testset(测试集) trainingset(训练集)
def SplitDataset(dataset,split,testset,trainingset):
for x in range(len(dataset)):
if random.random()<=split:
trainingset.append(dataset[x])
else:
testset.append(dataset[x])
#计算欧式距离 instance1(第一个坐标点) instance2(第二个坐标点) length(特征值个数)
def euclideanDistance(instance1,instance2,length):
distance=0
for x in range(length):
distance += pow((instance1[x] - instance2[x]), 2)
return math.sqrt(distance)
#选取距离最近的k个实例 testinstance(需要分类的测试集点)
def getNeighbors(trainingset,testinstance,k):
distances=[]
length=len(testinstance)-1
for x in range(len(trainingset)):
dis=euclideanDistance(trainingset[x],testinstance,length)
distances.append((trainingset[x],dis))
distances.sort(key=operator.itemgetter(1))
neighbors=[]
for x in range(k):
neighbors.append(distances[x][0])
return neighbors
#获取距离最近的k个实例中占比例较大的分类
def getResponse(neighbors):
classvotes={}
for x in range(len(neighbors)):
response=neighbors[x][-1]
if response in classvotes:
classvotes[response]+=1
else:
classvotes[response]=1
sortedVotes = sorted(classvotes.items(), key=operator.itemgetter(1), reverse=True)
return sortedVotes[0][0]
#计算准确率
def getAccuracy(testset,prediction):
correct=0
for x in range(len(testset)):
if testset[x][-1]==prediction[x]:
correct+=1
return correct/float(len(testset))*100.0
#用数字代表类别区分
def getPredict_target(prediction):
predict_target=[]
for x in range(len(prediction)):
if prediction[x]=='Iris-setosa':
predict_target.append(0)
if prediction[x]=='Iris-versicolor':
predict_target.append(1)
if prediction[x]=='Iris-virginica':
predict_target.append(2)
return predict_target
def main():
dataset=LoadIristdataset(r'C:\Users\SAMSUNG\Documents\iris_dataset.txt')
print(dataset)
trainingset=[]
testset=[]
SplitDataset(dataset,0.75,testset,trainingset)
print('划分出的训练集数量:')
print(len(trainingset))
print('划分出的测试集数量:')
print(len(testset))
prediction=[]
k=7
for x in range(len(testset)):
neighbors=getNeighbors(trainingset,testset[x],k)
result=getResponse(neighbors)
prediction.append(result)
accuracy=getAccuracy(testset,prediction)
print('准确率:')
print(accuracy)
target=getPredict_target(prediction)
#x,y坐标点
X = testset
L1 = [n[0] for n in X]
L2 = [n[1] for n in X]
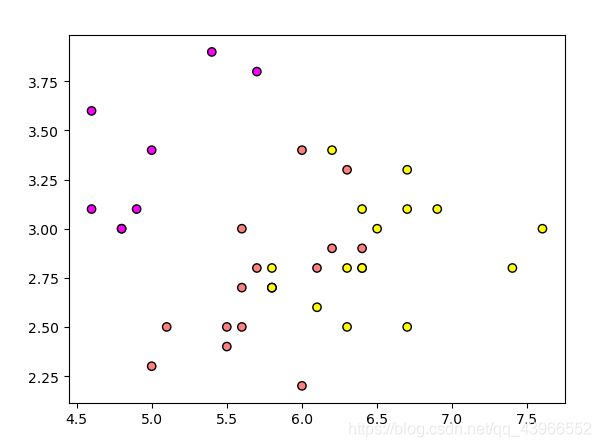
#画图
plt.scatter(L1, L2,c=target,cmap=plt.cm.spring, edgecolor='k')
plt.show()
main()
2.UCI Bank Marketing数据集用knn算法分类
import pandas as pd
import random
import math
import operator
import matplotlib.pyplot as plt
# 转换职业状态
# 'None', 'admin.', 'blue-collar', 'entrepreneur', 'housemaid', 'management', 'retired', 'self-employed','services','student', 'technician', 'unemployed', 'unknown'
def change_job(state):
job = ['None', 'admin.', 'blue-collar', 'entrepreneur', 'housemaid', 'management', 'retired', 'self-employed',
'services', 'student', 'technician', 'unemployed', 'unknown']
for i in range(len(job)):
if state == job[i]:
return i
# 转换婚姻状态
# 未知:0、单身:1、结婚:2、离婚:3
def change_marital(state):
marital = ['unknown', 'divorced', 'married', 'single']
for i in range(len(marital)):
if state == marital[i]:
return i
# 转换教育水平
# 未知:0、小学:1、中学:2、大学:3
def change_education(state):
education = ['unknown', 'primary', 'secondary', 'tertiary']
for i in range(len(education)):
if state == education[i]:
return i
# 二分类转换
# yes:1、no:0
def change_binary(state):
if state == 'yes':
state = 1
elif state == 'no':
state = 0
return state
# 转换接触方式
# 未知(unknown):0、网络(cellular):1、电话(telephone):2
def change_contact(state):
contact = ['unknown', 'cellular', 'telephone']
for i in range(len(contact)):
if state == contact[i]:
return i
# 转换poutcome(上次成功与否)
# failure:1、success:2、other:3、unknown:0
def change_poutcome(state):
poutcome = ['unknown', 'failure', 'other', 'success']
for i in range(len(poutcome)):
if state == poutcome[i]:
return i
def read(filename):
# 读取csv文件数据集
bank = pd.read_csv(filename, sep=';')
# 创建list
data = [[] for i in range(len(bank))]
# 逐个数据处理
for i in range(len(data)):
data[i].append(bank['age'][i])
data[i].append(change_job(bank['job'][i]))
data[i].append(change_marital(bank['marital'][i]))
data[i].append(change_education(bank['education'][i]))
data[i].append(change_binary(bank['default'][i]))
data[i].append(bank['balance'][i])
data[i].append(change_binary(bank['housing'][i]))
data[i].append(change_binary(bank['loan'][i]))
data[i].append(change_contact(bank['contact'][i]))
data[i].append(bank['duration'][i])
data[i].append(bank['campaign'][i])
data[i].append(bank['pdays'][i])
data[i].append(bank['previous'][i])
data[i].append(change_poutcome(bank['poutcome'][i]))
data[i].append(change_binary(bank['y'][i]))
#把数据转为浮点数类型
for x in range(len(data)):
for y in range(15):
data[x][y] = float(data[x][y])
return data
#拆分数据集 dataset(要拆分的数据集) split(训练集所占比例) testset(测试集) trainingset(训练集)
def splitdataset(dataset,split,trainingset,testset):
for x in range(len(dataset)):
if random.random()<=split:
trainingset.append(dataset[x])
else:
testset.append(dataset[x])
#计算欧式距离 instance1(第一个坐标点) instance2(第二个坐标点) length(特征值个数)
def euclideanDistance(instance1,instance2,length):
distance=0
for x in range(length):
distance += pow((instance1[x] - instance2[x]), 2)
return math.sqrt(distance)
#选取距离最近的k个实例 testinstance(需要分类的测试集点)
def getNeighbors(trainingset,testinstance,k):
distances=[]
length=len(testinstance)-1
for x in range(len(trainingset)):
dis=euclideanDistance(trainingset[x],testinstance,length)
distances.append((trainingset[x],dis))
distances.sort(key=operator.itemgetter(1))
neighbors=[]
for x in range(k):
neighbors.append(distances[x][0])
return neighbors
#获取距离最近的k个实例中占比例较大的分类
def getResponse(neighbors):
classvotes={}
for x in range(len(neighbors)):
response=neighbors[x][-1]
if response in classvotes:
classvotes[response]+=1
else:
classvotes[response]=1
sortedVotes = sorted(classvotes.items(), key=operator.itemgetter(1), reverse=True)
return sortedVotes[0][0]
#计算准确率
def getAccuracy(testset,prediction):
correct=0
for x in range(len(testset)):
if testset[x][-1]==prediction[x]:
correct+=1
return correct/float(len(testset))*100.0
def main():
filename = r"C:\Users\SAMSUNG\Desktop\bank.csv"
dataset = read(filename)
trainingset=[]
testset=[]
splitdataset(dataset,0.75,trainingset,testset)
print('划分出的训练集数量:')
print(len(trainingset))
print('划分出的测试集数量:')
print(len(testset))
prediction=[]
k=7
for x in range(len(testset)):
neighbors = getNeighbors(trainingset, testset[x], k)
result = getResponse(neighbors)
prediction.append(result)
accuracy=getAccuracy(testset,prediction)
print('准确率:')
print(accuracy)
# x,y坐标点
X = testset
L1 = [n[0] for n in X]
L2 = [n[5] for n in X]
L3 = [n[-1] for n in X]
# 画图
plt.scatter(L1, L2, c=L3, cmap=plt.cm.spring, edgecolor='k')
plt.show()
main()

二、贝叶斯分类算法原理
参考文章:
贝叶斯分类算法原理
算法公式详解
1.UCI Iris数据集用贝叶斯算法分类
对于全是数值类型的数据集,用公式:

计算类别。
import csv
import random
import operator
import math
import numpy as np
import matplotlib.pyplot as plt
#加载鸢尾花数据集 filename(数据存放路径)
def LoadIristdataset(filename):
with open(filename,'rt') as csvfile:
lines=csv.reader(csvfile)
data=list(lines)
for x in range(len(data)):
for y in range(4):
data[x][y]=float(data[x][y])
return data
#划分训练集和数据集 data(数据集) split(训练集所占比例) testset(测试集) trainingset(训练集)
def splitdata(data,split,trainingset,testset):
for i in range(len(data)):
if random.random()<split:
trainingset.append(data[i])
else:
testset.append(data[i])
#划分训练集中的三类数据(type1:Iris-setosa,type2:Iris-versicolor,type3:Iris-virginica)
def splittype(trainingset,state):
p=[]
for i in range(len(trainingset)):
if trainingset[i][-1]==state:
p.append(trainingset[i][0:4])
return p
#计算准确率
def getaccuracy(testset,prediction):
true=0.0
for i in range(len(testset)):
if testset[i][-1]==prediction[i]:
true+=1
return true/len(testset)*100
#贝叶斯分类算法预测种类
def countprobability(type1,type2,type3,testset,prediction):
for i in range(len(testset)):
p={}
pre={}
p['A|Iris-setosa']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[0]))*math.exp(-math.pow(testset[i][0]
-np.mean(type1,axis=0)[0],2)/(2*math.pow(np.var(type1,axis=0)[0],2)))
p['B|Iris-setosa']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[1]))*math.exp(-math.pow(testset[i][1]
-np.mean(type1,axis=0)[1],2)/(2*math.pow(np.var(type1,axis=0)[1],2)))
p['C|Iris-setosa']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[2]))*math.exp(-math.pow(testset[i][2]
-np.mean(type1,axis=0)[2],2)/(2*math.pow(np.var(type1,axis=0)[2],2)))
p['D|Iris-setosa']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[3]))*math.exp(-math.pow(testset[i][3]
-np.mean(type1,axis=0)[3],2)/(2*math.pow(np.var(type1,axis=0)[3],2)))
p['A|Iris-versicolor']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[0]))*math.exp(-math.pow(testset[i][0]
-np.mean(type2,axis=0)[0],2)/(2*math.pow(np.var(type2,axis=0)[0],2)))
p['B|Iris-versicolor']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[1]))*math.exp(-math.pow(testset[i][1]
-np.mean(type2,axis=0)[1],2)/(2*math.pow(np.var(type2,axis=0)[1],2)))
p['C|Iris-versicolor']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[2]))*math.exp(-math.pow(testset[i][2]
-np.mean(type2,axis=0)[2],2)/(2*math.pow(np.var(type2,axis=0)[2],2)))
p['D|Iris-versicolor']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[3]))*math.exp(-math.pow(testset[i][3]
-np.mean(type2,axis=0)[3],2)/(2*math.pow(np.var(type2,axis=0)[3],2)))
p['A|Iris-virginica']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type3,axis=0)[0]))*math.exp(-math.pow(testset[i][0]
-np.mean(type3,axis=0)[0],2)/(2*math.pow(np.var(type3,axis=0)[0],2)))
p['B|Iris-virginica']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type3,axis=0)[1]))*math.exp(-math.pow(testset[i][1]
-np.mean(type3,axis=0)[1],2)/(2*math.pow(np.var(type3,axis=0)[1],2)))
p['C|Iris-virginica']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type3,axis=0)[2]))*math.exp(-math.pow(testset[i][2]
-np.mean(type3,axis=0)[2],2)/(2*math.pow(np.var(type3,axis=0)[2],2)))
p['D|Iris-virginica']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type3,axis=0)[3]))*math.exp(-math.pow(testset[i][3]
-np.mean(type3,axis=0)[3],2)/(2*math.pow(np.var(type3,axis=0)[3],2)))
pre['Iris-setosa']=p['A|Iris-setosa']*p['B|Iris-setosa']*p['C|Iris-setosa']*p['D|Iris-setosa']
pre['Iris-versicolor']=p['A|Iris-versicolor']*p['B|Iris-versicolor']*p['C|Iris-versicolor']*p['D|Iris-versicolor']
pre['Iris-virginica']=p['A|Iris-virginica']*p['B|Iris-virginica']*p['C|Iris-virginica']*p['D|Iris-virginica']
type=sorted(pre.items(), key=operator.itemgetter(1), reverse=True)
prediction.append(type[0][0])
#用数字代表类别区分
def getPredict_target(prediction):
predict_target=[]
for x in range(len(prediction)):
if prediction[x]=='Iris-setosa':
predict_target.append(0)
if prediction[x]=='Iris-versicolor':
predict_target.append(1)
if prediction[x]=='Iris-virginica':
predict_target.append(2)
return predict_target
def main():
#加载数据集
data=LoadIristdataset(r'C:\Users\SAMSUNG\Documents\iris_dataset.txt')
print(data)
trainingset=[]
testset=[]
splitdata(data,0.75,trainingset,testset)
print('划分出的训练集数量:')
print(len(trainingset))
print('划分出的测试集数量:')
print(len(testset))
p={}
type1=splittype(trainingset,'Iris-setosa')
type2=splittype(trainingset,'Iris-versicolor')
type3=splittype(trainingset,'Iris-virginica')
prediction=[]
countprobability(type1,type2,type3,testset,prediction)
accuracy=getaccuracy(testset,prediction)
print('准确率:')
print(accuracy)
target = getPredict_target(prediction)
# x,y坐标点
X = testset
L1 = [n[0] for n in X]
L2 = [n[1] for n in X]
# 画图
plt.scatter(L1, L2, c=target, cmap=plt.cm.spring, edgecolor='k')
plt.show()
main()
实验结果:
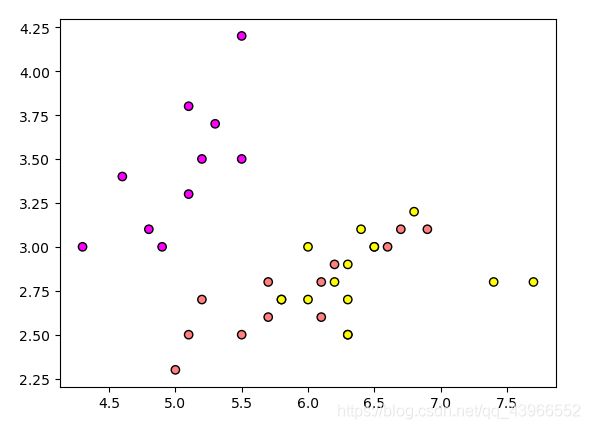
2.UCI Bank Marketing数据集用贝叶斯算法分类
对于有数值类型跟非数值类型的数据集,分为数值类型与非数值类型两部分,数值类型用公式:

非数值类型用公式:

来分类,最终类别概率的得出由数值类型类别概率乘上非数值类型类别概率。
import pandas as pd
import random
import math
import numpy as np
import operator
import matplotlib.pyplot as plt
#读取数据集
def read(filename):
# 读取csv文件数据集
bank = pd.read_csv(filename, sep=';')
# 创建list
data = [[] for i in range(len(bank))]
# 除去月份跟日
for i in range(len(data)):
data[i].append(bank['age'][i])
data[i].append(bank['job'][i])
data[i].append(bank['marital'][i])
data[i].append(bank['education'][i])
data[i].append(bank['default'][i])
data[i].append(bank['balance'][i])
data[i].append(bank['housing'][i])
data[i].append(bank['loan'][i])
data[i].append(bank['contact'][i])
data[i].append(bank['duration'][i])
data[i].append(bank['campaign'][i])
data[i].append(bank['pdays'][i])
data[i].append(bank['previous'][i])
data[i].append(bank['poutcome'][i])
data[i].append(bank['y'][i])
return data
#划分出训练集和测试集
def splitdata(data,split,trainingset,testset):
for i in range(len(data)):
if random.random()<split:
trainingset.append(data[i])
else:
testset.append(data[i])
#对训练集分类
def splittype(trainingset,state):
p=[]
for i in range(len(trainingset)):
if trainingset[i][-1]==state:
p.append(trainingset[i][0:6])
return p
#计算某一列中的某个特征属性的数量 columns(列号) state(值)
def countnum(strtype,columns,state):
count=0
for i in range(len(strtype)):
if strtype[i][columns]==state:
count+=1
return count
#计算某一列中的某两个特征属性同时存在的行数
def countnum2(strtype,columns,state1,state2):
count=0
for i in range(len(strtype)):
if strtype[i][columns]==state1 and strtype[i][-1]==state2:
count+=1
return count
#计算概率
def countstrtypeprobability(strtype,p2,type1,type2):
p2['jobadmin.|yes']=countnum2(strtype,0,'admin.','yes')/len(type1)
p2['jobblue-collar|yes']=countnum2(strtype,0,'blue-collar','yes')/len(type1)
p2['jobentrepreneur|yes']=countnum2(strtype,0,'entrepreneur','yes')/len(type1)
p2['jobhousemaid|yes']=countnum2(strtype,0,'housemaid','yes')/len(type1)
p2['jobmanagement|yes']=countnum2(strtype,0,'management','yes')/len(type1)
p2['jobretired|yes']=countnum2(strtype,0,'retired','yes')/len(type1)
p2['jobself-employed|yes']=countnum2(strtype,0,'self-employed','yes')/len(type1)
p2['jobservices|yes']=countnum2(strtype,0,'services','yes')/len(type1)
p2['jobstudent|yes']=countnum2(strtype,0,'student','yes')/len(type1)
p2['jobtechnician|yes']=countnum2(strtype,0,'technician','yes')/len(type1)
p2['jobunemployed|yes']=countnum2(strtype,0,'unemployed','yes')/len(type1)
p2['jobunknown|yes']=countnum2(strtype,0,'unknown','yes')/len(type1)
p2['maritaldivorced|yes']=countnum2(strtype,1,'divorced','yes')/len(type1)
p2['maritalmarried|yes']=countnum2(strtype,1,'married','yes')/len(type1)
p2['maritalsingle|yes']=countnum2(strtype,1,'single','yes')/len(type1)
p2['educationunknown|yes']=countnum2(strtype,2,'unknown','yes')/len(type1)
p2['educationprimary|yes']=countnum2(strtype,2,'primary','yes')/len(type1)
p2['educationsecondary|yes']=countnum2(strtype,2,'secondary','yes')/len(type1)
p2['educationtertiary|yes']=countnum2(strtype,2,'tertiary','yes')/len(type1)
p2['defaultyes|yes']=countnum2(strtype,3,'yes','yes')/len(type1)
p2['defaultno|yes']=countnum2(strtype,3,'no','yes')/len(type1)
p2['housingyes|yes']=countnum2(strtype,4,'yes','yes')/len(type1)
p2['housingno|yes']=countnum2(strtype,4,'no','yes')/len(type1)
p2['loanyes|yes']=countnum2(strtype,5,'yes','yes')/len(type1)
p2['loanno|yes']=countnum2(strtype,5,'no','yes')/len(type1)
p2['contactunknown|yes']=countnum2(strtype,6,'unknown','yes')/len(type1)
p2['contactcellular|yes']=countnum2(strtype,6,'cellular','yes')/len(type1)
p2['contacttelephone|yes']=countnum2(strtype,6,'telephone','yes')/len(type1)
p2['poutcomeunknown|yes']=countnum2(strtype,7,'unknown','yes')/len(type1)
p2['poutcomefailure|yes']=countnum2(strtype,7,'failure','yes')/len(type1)
p2['poutcomeother|yes']=countnum2(strtype,7,'other','yes')/len(type1)
p2['poutcomesuccess|yes']=countnum2(strtype,7,'success','yes')/len(type1)
p2['jobadmin.|no']=countnum2(strtype,0,'admin.','no')/len(type2)
p2['jobblue-collar|no'] = countnum2(strtype,0,'blue-collar','no')/len(type2)
p2['jobentrepreneur|no']=countnum2(strtype,0,'entrepreneur','no')/len(type2)
p2['jobhousemaid|no']=countnum2(strtype,0,'housemaid','no')/len(type2)
p2['jobmanagement|no']=countnum2(strtype,0,'management','no')/len(type2)
p2['jobretired|no']=countnum2(strtype,0,'retired','no')/len(type2)
p2['jobself-employed|no']=countnum2(strtype,0,'self-employed','no')/len(type2)
p2['jobservices|no']=countnum2(strtype,0,'services','no')/len(type2)
p2['jobstudent|no']=countnum2(strtype,0,'student','no')/len(type2)
p2['jobtechnician|no']=countnum2(strtype,0,'technician','no')/len(type2)
p2['jobunemployed|no']=countnum2(strtype,0,'unemployed','no')/len(type2)
p2['jobunknown|no']=countnum2(strtype,0,'unknown','no')/len(type2)
p2['maritaldivorced|no']=countnum2(strtype,1,'divorced','no')/len(type2)
p2['maritalmarried|no']=countnum2(strtype,1,'married','no')/len(type2)
p2['maritalsingle|no']=countnum2(strtype,1,'single','no')/len(type2)
p2['educationunknown|no']=countnum2(strtype,2,'unknown','no')/len(type2)
p2['educationprimary|no']=countnum2(strtype,2,'primary','no')/len(type2)
p2['educationsecondary|no']=countnum2(strtype,2,'secondary','no')/len(type2)
p2['educationtertiary|no']=countnum2(strtype,2,'tertiary','no')/len(type2)
p2['defaultyes|no']=countnum2(strtype,3,'yes','no')/len(type2)
p2['defaultno|no']=countnum2(strtype,3,'no','no')/len(type2)
p2['housingyes|no']=countnum2(strtype,4,'yes','no')/len(type2)
p2['housingno|no']=countnum2(strtype,4,'no','no')/len(type2)
p2['loanyes|no']=countnum2(strtype,5,'yes','no')/len(type2)
p2['loanno|no']=countnum2(strtype,5,'no','no')/len(type2)
p2['contactunknown|no']=countnum2(strtype,6,'unknown','no')/len(type2)
p2['contactcellular|no']=countnum2(strtype,6,'cellular','no')/len(type2)
p2['contacttelephone|no']=countnum2(strtype,6,'telephone','no')/len(type2)
p2['poutcomeunknown|no']=countnum2(strtype,7,'unknown','no')/len(type2)
p2['poutcomefailure|no']=countnum2(strtype,7,'failure','no')/len(type2)
p2['poutcomeother|no']=countnum2(strtype,7,'other','no')/len(type2)
p2['poutcomesuccess|no']=countnum2(strtype,7,'success','no')/len(type2)
p2['jobadmin.']=countnum(strtype,0,'admin.')/len(strtype)
p2['jobblue-collar']=countnum(strtype,0,'blue-collar')/len(strtype)
p2['jobentrepreneur']=countnum(strtype,0,'entrepreneur')/len(strtype)
p2['jobhousemaid']=countnum(strtype,0,'housemaid')/len(strtype)
p2['jobmanagement']=countnum(strtype,0,'management')/len(strtype)
p2['jobretired']=countnum(strtype,0,'retired')/len(strtype)
p2['jobself-employed']=countnum(strtype,0,'self-employed')/len(strtype)
p2['jobservices']=countnum(strtype,0,'services')/len(strtype)
p2['jobstudent']=countnum(strtype,0,'student')/len(strtype)
p2['jobtechnician']=countnum(strtype,0,'technician')/len(strtype)
p2['jobunemployed']=countnum(strtype,0,'unemployed')/len(strtype)
p2['jobunknown']=countnum(strtype,0,'unknown')/len(strtype)
p2['maritaldivorced']=countnum(strtype,1,'divorced')/len(strtype)
p2['maritalmarried']=countnum(strtype,1,'married')/len(strtype)
p2['maritalsingle']=countnum(strtype,1,'single')/len(strtype)
p2['educationunknown']=countnum(strtype,2,'unknown')/len(strtype)
p2['educationprimary']=countnum(strtype,2,'primary')/len(strtype)
p2['educationsecondary']=countnum(strtype,2,'secondary')/len(strtype)
p2['educationtertiary']=countnum(strtype,2,'tertiary')/len(strtype)
p2['defaultyes']=countnum(strtype,3,'yes')/len(strtype)
p2['defaultno']=countnum(strtype,3,'no')/len(strtype)
p2['housingyes']=countnum(strtype,4,'yes')/len(strtype)
p2['housingno']=countnum(strtype,4,'no')/len(strtype)
p2['loanyes']=countnum(strtype,5,'yes')/len(strtype)
p2['loanno']=countnum(strtype,5,'no')/len(strtype)
p2['contactunknown']=countnum(strtype,6,'unknown')/len(strtype)
p2['contactcellular']=countnum(strtype,6,'cellular')/len(strtype)
p2['contacttelephone']=countnum(strtype,6,'telephone')/len(strtype)
p2['poutcomeunknown']=countnum(strtype,7,'unknown')/len(strtype)
p2['poutcomefailure']=countnum(strtype,7,'failure')/len(strtype)
p2['poutcomeother']=countnum(strtype,7,'other')/len(strtype)
p2['poutcomesuccess']=countnum(strtype,7,'success')/len(strtype)
p2['yes']=len(type1)/len(strtype)
p2['no']=len(type2)/len(strtype)
#贝叶斯分类算法预测种类
def countprobability(trainingset,testset,prediction):
p2={}
pre={}
numtype=[[] for i in range(len(trainingset))]
strtype=[[] for i in range(len(trainingset))]
#划分数值类型数据和非数值类型数据
#numtype=['age','balance','duration','campaign','pdays','previous']
#strtype=['job','marital','education','default','housing','loan','contact','poutcome']
for i in range(len(trainingset)):
numtype[i].append(trainingset[i][0])
strtype[i].append(trainingset[i][1])
strtype[i].append(trainingset[i][2])
strtype[i].append(trainingset[i][3])
strtype[i].append(trainingset[i][4])
numtype[i].append(trainingset[i][5])
strtype[i].append(trainingset[i][6])
strtype[i].append(trainingset[i][7])
strtype[i].append(trainingset[i][8])
numtype[i].append(trainingset[i][9])
numtype[i].append(trainingset[i][10])
numtype[i].append(trainingset[i][11])
numtype[i].append(trainingset[i][12])
strtype[i].append(trainingset[i][13])
numtype[i].append(trainingset[i][14])
strtype[i].append(trainingset[i][14])
type1=splittype(numtype,'yes')
type2=splittype(numtype,'no')
countstrtypeprobability(strtype,p2,type1,type2)
# 贝叶斯分类算法预测种类
for i in range(len(testset)):
p1={}
p1['age|yes']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[0]))*math.exp(-math.pow(testset[i][0]
-np.mean(type1,axis=0)[0],2)/(2*math.pow(np.var(type1,axis=0)[0],2)))
p1['balance|yes']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[1]))*math.exp(-math.pow(testset[i][5]
-np.mean(type1,axis=0)[1],2)/(2*math.pow(np.var(type1,axis=0)[1],2)))
p1['duration|yes']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[2]))*math.exp(-math.pow(testset[i][9]
-np.mean(type1,axis=0)[2],2)/(2*math.pow(np.var(type1,axis=0)[2],2)))
p1['campaign|yes']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[3]))*math.exp(-math.pow(testset[i][10]
-np.mean(type1,axis=0)[3],2)/(2*math.pow(np.var(type1,axis=0)[3],2)))
p1['pdays|yes']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[4]))*math.exp(-math.pow(testset[i][11]
-np.mean(type1,axis=0)[4],2)/(2*math.pow(np.var(type1,axis=0)[4],2)))
p1['previous|yes']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type1,axis=0)[5]))*math.exp(-math.pow(testset[i][12]
-np.mean(type1,axis=0)[5],2)/(2*math.pow(np.var(type1,axis=0)[5],2)))
p1['numtype|yes']=p1['age|yes']*p1['balance|yes']*p1['duration|yes']*p1['campaign|yes']*p1['pdays|yes']*p1['previous|yes']
p1['strtype|yes']=p2['job'+strtype[i][0]+'|yes']*p2['marital'+strtype[i][1]+'|yes']*p2['education'+strtype[i][2]+'|yes']*p2['default'+strtype[i][3]+'|yes']\
*p2['housing'+strtype[i][4]+'|yes']*p2['loan'+strtype[i][5]+'|yes']*p2['contact'+strtype[i][6]+'|yes']*p2['poutcome'+strtype[i][7]+'|yes']\
*p2['yes']/(p2['job'+strtype[i][0]]*p2['marital'+strtype[i][1]]*p2['education'+strtype[i][2]]*p2['default'+strtype[i][3]]*p2['housing'+strtype[i][4]]
*p2['loan'+strtype[i][5]]*p2['contact'+strtype[i][6]]*p2['poutcome'+strtype[i][7]])
pre['yes']=p1['numtype|yes']*p1['strtype|yes']
p1['age|no']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[0]))*math.exp(-math.pow(testset[i][0]
-np.mean(type2,axis=0)[0],2)/(2*math.pow(np.var(type2,axis=0)[0],2)))
p1['balance|no']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[1]))*math.exp(-math.pow(testset[i][5]
-np.mean(type2,axis=0)[1],2)/(2*math.pow(np.var(type2,axis=0)[1],2)))
p1['duration|no']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[2]))*math.exp(-math.pow(testset[i][9]
-np.mean(type2,axis=0)[2],2)/(2*math.pow(np.var(type2,axis=0)[2],2)))
p1['campaign|no']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[3]))*math.exp(-math.pow(testset[i][10]
-np.mean(type2,axis=0)[3],2)/(2*math.pow(np.var(type2,axis=0)[3],2)))
p1['pdays|no']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[4]))*math.exp(-math.pow(testset[i][11]
-np.mean(type2,axis=0)[4],2)/(2*math.pow(np.var(type2,axis=0)[4],2)))
p1['previous|no']=1.0/(math.sqrt(2*3.14)*math.sqrt(np.var(type2,axis=0)[5]))*math.exp(-math.pow(testset[i][12]
-np.mean(type2,axis=0)[5],2)/(2*math.pow(np.var(type2,axis=0)[5],2)))
p1['numtype|no']=p1['age|no']*p1['balance|no']*p1['duration|no']*p1['campaign|no']*p1['pdays|no']*p1['previous|no']
p1['strtype|no']=p2['job'+strtype[i][0]+'|no']*p2['marital'+strtype[i][1]+'|no']*p2['education'+strtype[i][2]+'|no']*p2['default'+strtype[i][3]+'|no']\
*p2['housing'+strtype[i][4]+'|no']*p2['loan'+strtype[i][5]+'|no']*p2['contact'+strtype[i][6]+'|no']*p2['poutcome'+strtype[i][7]+'|no']\
*p2['no']/(p2['job'+strtype[i][0]]*p2['marital'+strtype[i][1]]*p2['education'+strtype[i][2]]*p2['default'+strtype[i][3]]*p2['housing'+strtype[i][4]]
*p2['loan'+strtype[i][5]]*p2['contact'+strtype[i][6]]*p2['poutcome'+strtype[i][7]])
pre['no']=p1['numtype|no']*p1['strtype|no']
#从大到小排序
type = sorted(pre.items(), key=operator.itemgetter(1), reverse=True)
prediction.append(type[0][0])
#计算准确率
def getaccuracy(testset,prediction):
true=0.0
for i in range(len(testset)):
if testset[i][-1]==prediction[i]:
true+=1
return true/len(testset)*100
def main():
filename = r"C:\Users\SAMSUNG\Desktop\bank.csv"
data = read(filename)
trainingset=[]
testset=[]
splitdata(data,0.75,trainingset,testset)
print('划分出的训练集数量:')
print(len(trainingset))
print('划分出的测试集数量:')
print(len(testset))
prediction=[]
countprobability(trainingset,testset,prediction)
accuracy = getaccuracy(testset, prediction)
print('准确率:')
print(accuracy)
##用数字代表类别区分
for i in range(len(testset)):
if testset[i][-1]=='yes':
testset[i][-1]=1
else:testset[i][-1]=0
# x,y坐标点
X = testset
L1 = [n[0] for n in X]
L2 = [n[5] for n in X]
L3 = [n[-1] for n in X]
# 画图
plt.scatter(L1, L2, c=L3, cmap=plt.cm.spring, edgecolor='k')
plt.show()
main()
实验结果:


总结:
我做的实验发现,两种数据用knn分类算法的准确率要高于贝叶斯分类算法。Knn分类算法准确率与k值的选择有关,所以可以通过调节k值大小找到最合适的值进而提高准确率;贝叶斯分类算法准确率与数据的概率有关。我做的第一个数据集量少且均为数值类型数据用两种算法准确率都是90%左右;第二个数据集量多且数值类型与非数值类型数据混合用两种算法准确率都是85%左右,其中第二个数据集用贝叶斯分类算法,由于数据量大计算的概率多,代码运行时长需要2min左右。