知识卡片 信息熵
![]()
前言:本文讲解了机器学习需要用到的信息论中关于信息熵的知识,并用代码演示如何计算信息熵和互信息。
信息熵 Information Entropy
信息论中的熵(entropy)
信息熵
log(1/p)的图像如下,是单调递减函数,不确定性越大,事件发生的概率越小。需要指出的是,H(U)式子中的对数是以2为底数,信息熵的单位是比特;在sklearn中,以自然对数e为底。
交叉熵 cross entropy
交叉熵在神经网络中可以作为损失函数,用于衡量模型预测和真实的差异。
相对熵 relative entropy
应用举例:
条件概率中,以B来模拟A的真实情况所需要的相对熵更小,更接近真实。
相对熵的性质:
相对熵看似可以度量距离,实际上不具有对称性,也不满足三角不等式,因而不能度量距离。「KL散度」有时也被称为『KL距离』,实际上它度量不是真正的距离,度量的是两个分布的相似程度。
JS散度
联合熵 Joint Entropy
条件熵 the conditional entropy
推导公式中,yj是某个已知的随机变量的分布,红色和蓝色部分的推导公式,用条件概率公式换算,最后得到的蓝色式子由对数相除变减法,拆开后分别符合联合熵和信息熵的定义。
互信息 Mututal Information
式中红色是互信息的定义,蓝色为推导,互信息具有对称性 I(x,y) = I(y,x)。
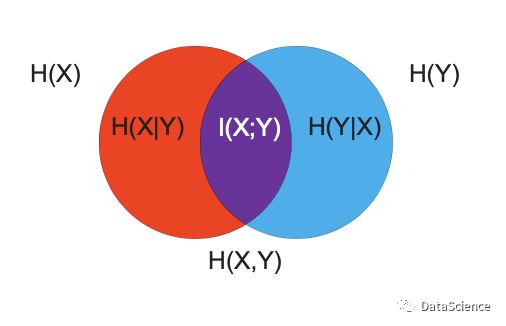
文氏图图解
左右两边各位X和Y的信息熵也可以称为边缘熵,红色和蓝色圆圈的部分是X和Y的条件熵,中间紫色部分是互信息,两个圆重叠的部分是联合熵。
代码演示-信息熵和互信息的计算
演示内容:香农信息熵的计算(例1和例2分别为两种不同类型的输入)以及互信息的计算(例3)。其中log默认为自然对数。
代码如下:
import numpy as np
from math import log
#例1:计算信息熵(x1,x2,x3 已知概率分布)
print("例1:")
def calc_ent(x):
ent = 0.0 # entropy 熵
for p in x:
ent -= p * np.log(p) # 信息熵计算公式
return ent
x1=np.array([0.4, 0.2, 0.2, 0.2]) # 概率分布 第一个信号的概率0.4 ....
x2=np.array([1]) # 肯定发生
x3=np.array([0.2, 0.2, 0.2, 0.2, 0.2]) # 五个信号发生的概率相同
print ("x1的信息熵:", calc_ent(x1))
print ("x2的信息熵:", calc_ent(x2))
print ("x3的信息熵:", calc_ent(x3))
print("")
'''
例1:
x1的信息熵: 1.3321790402101223
x2的信息熵: 0.0
x3的信息熵: 1.6094379124341005
'''
#例2:计算信息熵(此时给定了信号发生情况,需要要计算概率)
print("例2:")
def calcShannonEnt(dataSet):
length,dataDict=float(len(dataSet)),{}
# 获取数据集长度,字典存放信号名称和次数
for data in dataSet: # 遍历数据集,统计各事件发生的次数
try:dataDict[data]+=1
except:dataDict[data]=1
return sum([-d/length*log(d/length) for d in list(dataDict.values())])
# 例2中x1,x2,x3的信号发生的概率和例一种x1,x2,x3的概率相同
print("x1的信息熵:", calcShannonEnt(['A','B','C','D','A']))
print("x2的信息熵:",calcShannonEnt(['A','A','A','A','A']))
print("x3的信息熵:",calcShannonEnt(['A','B','C','D','E']))
'''
例2:
x1的信息熵: 1.3321790402101223
x2的信息熵: 0.0
x3的信息熵: 1.6094379124341005
'''
#例3:计算互信息(输入:给定的信号发生情况,其中联合分布手工给出)
print("")
print("例3:")
# 根据互信息的计算公式,I(x;y)=H(x)+H(y)-H(x,y),仍然使用例2中的函数
Ent_x4=calcShannonEnt(['3', '4', '5', '5', '3', '2', '2', '6', '6', '1'])
Ent_x5=calcShannonEnt(['7', '2', '1', '3', '2', '8', '9', '1', '2', '0'])
Ent_x4x5=calcShannonEnt(['37', '42', '51', '53', '32', '28', '29', '61', '62', '10', '37', '42'])
MI_x4_x5=Ent_x4+Ent_x5-Ent_x4x5
print ("x4和x5之间的互信息:",MI_x4_x5)
'''
例3:
x4和x5之间的互信息: 1.3285817292263604
'''
![]()
好文章,我 在看❤