pandas基础1

预备阶段

Python 基础

语法糖

列表推导式

• 生成一个数字序列:

 L=[]
def my_fuction(x):
    return 2*x

for i in range(5):
        L.append(my_fuction(i)) #append() 方法用于在列表末尾添加新的对象
L

[0, 2, 4, 6, 8]

• 用列表推导式进行简化([* for i in *]):

[my_fuction(i) for i in range(5)]

[0, 2, 4, 6, 8]

• 列表表达式还支持多层嵌套，如下面的例子中第一个 for 为外层循环，第二个为内层循环：

[m+"_"+n for m in['a','b'] for n in ['c','d']]

['a_c', 'a_d', 'b_c', 'b_d']

条件赋值

• 除了列表推导式，另一个实用的语法糖是条件赋值，其形式为 value = a if condition else b (使用语法糖能够增加程序的可读性)

value="cat" if 2>1 else "dog"

value

'cat'

• 等价于如下的写法：

a,b="cat","dog"
condition=2>1
if condition:
    value=a
else:
    value=b

value

'cat'

例：截断列表中超过 5 的元素：

L=[1,2,3,4,5,6,7]
[i if i<=5 else 5 for i in L]

[1, 2, 3, 4, 5, 5, 5]

匿名函数与 map 方法

有一些函数的定义具有清晰简单的映射关系，例如上面的 my_func 函数，这时候可以用匿名函数的方法简洁地表示.

以下两行代码只是介绍了lambda的用法，但是并非真正的匿名函数使用。

my_fuc=lambda x :2*x
my_fuc(3)

6

my_fuc=lambda a,b:a+b
my_fuc(2,3)

5

但上面的用法其实违背了“匿名”的含义，事实上它往往在无需多处调用的场合进行使用，例如上面列表推导式中的例子，用户不关心函数的名字，只关心这种映射的关系：

[(lambda x:2*x) (i)for i in range(5)]

[0, 2, 4, 6, 8]

对于上述的这种列表推导式的匿名函数映射， Python 中提供了 map 函数来完成，它返回的是一个 map 对象，需要通过 list 转为列表：

map((lambda x :2*x),range(5))  #返回一个map对象

list(map((lambda x :2*x),range(5)))  #map对象用list转换为列表

[0, 2, 4, 6, 8]

对于多个输入值的函数映射，可以通过追加迭代对象实现：

list(map((lambda a,b:str(a)+'_'+b),range(5),list('abcde'))) #在默写的时候没有在a前写str，没有在abcde外加引号、前写list

['0_a', '1_b', '2_c', '3_d', '4_e']

zip 对象与 enumerate 方法

zip打包

zip 函数能够把多个可迭代对象打包成一个元组构成的可迭代对象，它返回了一个 zip 对象，通过 tuple, list
可以得到相应的打包结果：

L1,L2,L3=list('abc'),list('edf'),list('ghi')
list(zip(L1,L2,L3))

[('a', 'e', 'g'), ('b', 'd', 'h'), ('c', 'f', 'i')]

tuple(zip(L1,L2,L3))

(('a', 'e', 'g'), ('b', 'd', 'h'), ('c', 'f', 'i'))

for i,j,k in zip(L1,L2,L3):
    print (i,j,k)

a e g
b d h
c f i

enumerate打包

enumerate 是一种特殊的打包，它可以在迭代时绑定迭代元素的遍历序号（直接绑定序号和L的每个值）：

L=list('abcd')
for i,j in enumerate(L):
    print (i,j)

0 a
1 b
2 c
3 d

用 zip 对象也能够简单地实现这个功能(输出序号和L的每个值）：

for i,j in zip(range(len(L)),L):
    print (i,j)

0 a
1 b
2 c
3 d

字典映射也可利用 zip 对象：

dict(zip(L1,L2))   #L1内元素为键，L2内元素为值

{'a': 'e', 'b': 'd', 'c': 'f'}

解压操作( * 操作符和 zip 联合使用)：

L4=list(zip(L1,L2,L3))
L4

[('a', 'e', 'g'), ('b', 'd', 'h'), ('c', 'f', 'i')]

list(zip(*L4))  

[('a', 'b', 'c'), ('e', 'd', 'f'), ('g', 'h', 'i')]

Numpy 基础

np 数组的构造

通过 array 构造

import numpy as np
np.array([1,2,3])

array([1, 2, 3])

等差序列： np.linspace, np.arange

np.linspace(1,2,5) #起始、终止、包含样本个数

array([1.  , 1.25, 1.5 , 1.75, 2.  ])

np.arange(1,5,2) #起始、终止、步长

array([1, 3])

特殊矩阵： zeros, eye, full

np.zeros((2,3))  #数字表维度大小

array([[0., 0., 0.],
       [0., 0., 0.]])

np.eye(3)  #数字表示单位阵规模

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

np.eye(3,k=-1) #偏移主对角线一个单位的伪单位矩阵

array([[0., 0., 0.],
       [1., 0., 0.],
       [0., 1., 0.]])

np.full((2,3),10)  #元组规模和填充数值

array([[10, 10, 10],
       [10, 10, 10]])

np.full((2,3),[1,2,3]) #元组规模和传入列表（用于填充每列？）

array([[1, 2, 3],
       [1, 2, 3]])

随机矩阵： np.random

最常用的随机生成函数为 rand, randn, randint, choice ，它们分别表示 0-1 均匀分布的随机数组、标准正态
的随机数组、随机整数组和随机列表抽样：

np.random.rand(3)  #随机生成3个服从0-1分布的随机数

array([0.8919139 , 0.08891588, 0.84276902])

np.random.rand(3,3)

array([[0.60106419, 0.01510629, 0.17511632],
       [0.33475289, 0.85297977, 0.38752512],
       [0.8368472 , 0.18000487, 0.32388913]])

生成区间a到b上的均匀分布的随机数如下：

a,b=5,15
(b-a)*np.random.rand(3)+a

array([12.81679494,  7.51306834, 10.78464292])

生成服从正态N（0，1）分布的随机数

np.random.randn(3)

array([-0.44134042,  0.65540442,  0.72383828])

np.random.randn(3,3)

array([[-1.98115902, -0.38039706,  0.70033863],
       [ 0.78964238, -1.35473175,  0.0678929 ],
       [-0.35582863,  0.59269786,  0.58837349]])

生成服从非标准正态分布的随机数

sigma,mu=3,2
sigma*(np.random.randn(3))+mu

array([1.46263526, 3.70204291, 0.70029179])

randint 可以指定生成随机整数的最小值最大值和维度大小：

low,high,size=0,2,(2,2)
np.random.randint(low,high,size)

array([[1, 0],
       [0, 0]])

choice 可以从给定的列表中，以一定概率和方式抽取结果，当不指定概率时为均匀采样，默认抽取方式为有放回抽样：

list=['a','b','c','d']
np.random.choice(list,2,replace=False,p=(0.1,0.3,0.2,0.4))

array(['b', 'd'], dtype='

np.random.choice(list,(3,3))

array([['b', 'd', 'b'],
       ['b', 'b', 'a'],
       ['d', 'c', 'd']], dtype='

使用 permutation 函数可打散原列表（或令返回的元素个数与原列表相同）

np.random.permutation(list)

array(['b', 'c', 'd', 'a'], dtype='

随机种子能固定随机数的输出结果：

np.random.seed(20201216)
np.random.rand(3)

array([0.25782161, 0.44401886, 0.17936431])

np.random.rand(3)

array([0.79508033, 0.26673911, 0.59714383])

np.random.seed(20201216)
np.random.rand(3)

array([0.25782161, 0.44401886, 0.17936431])

np 数组的变形与合并

转置： T

np.zeros((2,3)).T

array([[0., 0.],
       [0., 0.],
       [0., 0.]])

合并操作： r_, c_

对于二维数组而言， r_ 和 c_ 分别表示上下合并和左右合并：

np.r_[np.zeros((2,3)),np.zeros((2,3))]

array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])

np.c_[np.zeros((2,3)),np.zeros((2,3))]

array([[0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0.]])

一维数组和二维数组进行合并时，应当把其视作列向量，在长度匹配的情况下只能够使用左右合并的 c_ 操作：

np.r_[np.array([0,0]),np.zeros((2,1))]

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

 in 
----> 1 np.r_[np.array([0,0]),np.zeros((2,1))]


D:\Anaconda3\lib\site-packages\numpy\lib\index_tricks.py in __getitem__(self, key)
    404                 objs[k] = objs[k].astype(final_dtype)
    405 
--> 406         res = self.concatenate(tuple(objs), axis=axis)
    407 
    408         if matrix:


<__array_function__ internals> in concatenate(*args, **kwargs)


ValueError: all the input arrays must have same number of dimensions, but the array at index 0 has 1 dimension(s) and the array at index 1 has 2 dimension(s)

np.r_[np.array([0,0]),np.zeros(2)]

array([0., 0., 0., 0.])

 np.c_[np.array([0,0]),np.zeros((2,3))]

array([[0., 0., 0., 0.],
       [0., 0., 0., 0.]])

维度变换： reshape

reshape 能够帮助用户把原数组按照新的维度重新排列。在使用时有两种模式，分别为 C 模式和 F 模式，分别以逐行和逐列的顺序进行填充读取。

一维数组按行列读取

np.arange(8)

array([0, 1, 2, 3, 4, 5, 6, 7])

np.arange(8).reshape(2,4)  #默认按行（C）读取

array([[0, 1, 2, 3],
       [4, 5, 6, 7]])

np.arange(8).reshape((2,4),order='F')

array([[0, 2, 4, 6],
       [1, 3, 5, 7]])

二维数组按行列读取

target=np.arange(8).reshape(2,4)
target

array([[0, 1, 2, 3],
       [4, 5, 6, 7]])

target.reshape((4,2),order='C')  #按行读取和填充

array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7]])

target.reshape((4,2),order='F')  #按列读取和填充

array([[0, 2],
       [4, 6],
       [1, 3],
       [5, 7]])

特别地，由于被调用数组的大小是确定的， reshape 允许有一个维度存在空缺，此时只需填充-1 即可：

target.reshape(4,-1)

array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7]])

下面将 n*1 大小的数组转为 1 维数组的操作是经常使用的

target = np.ones((3,1))
target

array([[1.],
       [1.],
       [1.]])

target.reshape(-1)

array([1., 1., 1.])

np 数组的切片与索引

数组的切片模式支持使用 slice 类型的 startstep 切片，还可以直接传入列表指定某个维度的索引进行切片：

target = np.arange(9).reshape(3,3)
target

array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

 target[:-1, [0,2]]   #从第一行一直到倒数第一行，零列和2列

array([[0, 2],
       [3, 5]])

此外，还可以利用 np.ix_ 在对应的维度上使用布尔索引，但此时不能使用 slice 切片：

target[np.ix_([True, False, True], [True, False, True])]  #选需要哪几行，再选需要哪几列

array([[0, 2],
       [6, 8]])

target[np.ix_([1,2], [True, False, True])]

array([[3, 5],
       [6, 8]])

当数组维度为 1 维时，可以直接进行布尔索引，而无需 np.ix_ ：

new = target.reshape(-1)

new[new%2==0]   #恒为偶数

array([0, 2, 4, 6, 8])

常见函数

为了简单起见，这里假设下述函数输入的数组都是一维的。

where

where 是一种条件函数，可以指定满足条件与不满足条件位置对应的填充值：

a = np.array([-1,1,-1,0])
np.where(a>0, a, 5) # 对应位置为 True 时填充 a 对应元素，否则填充 5

array([5, 1, 5, 5])

nonzero, argmax, argmin

这三个函数返回的都是索引， nonzero 返回非零数的索引， argmax, argmin 分别返回最大和最小数的索引：

a = np.array([-2,-5,0,1,3,-1])  
a  

array([-2, -5,  0,  1,  3, -1])

 np.nonzero(a)

(array([0, 1, 3, 4, 5], dtype=int64),)

np.argmax(a)

4

np.argmin(a)

1

any, all

any 指当序列至少 存在一个 True 或非零元素时返回 True ，否则返回 False

all 指当序列元素 全为 True 或非零元素时返回 True ，否则返回 False

 a = np.array([0,1])
a.any()

True

a.all()

False

cumprod, cumsum, diff

cumprod, cumsum 分别表示累乘和累加函数，返回同长度的数组， diff 表示和前一个元素做差，由于第一个
元素为缺失值，因此在默认参数情况下，返回长度是原数组减1

a = np.array([1,2,3])
a.cumprod()

array([1, 2, 6], dtype=int32)

a.cumsum()

array([1, 3, 6], dtype=int32)

np.diff(a)

array([1, 1])

统计函数

常用的统计函数包括 max, min, mean, median, std, var, sum, quantile ，其中分位数计算是全局方法，因此不能通过 array.quantile 的方法调用：

 target = np.arange(5)
target

array([0, 1, 2, 3, 4])

target.max()

4

 np.quantile(target, 0.5) # 0.5 分位数

2.0

但是对于含有缺失值的数组，它们返回的结果也是缺失值，如果需要略过缺失值，必须使用 nan* 类型的函
数，上述的几个统计函数都有对应的 nan* 函数。

target = np.array([1, 2, np.nan])
target

array([ 1.,  2., nan])

target.max()

nan

np.nanmax(target)

2.0

np.nanquantile(target, 0.5)

1.5

对于协方差和相关系数分别可以利用 cov, corrcoef 如下计算：

target1 = np.array([1,3,5,9])
target2 = np.array([1,5,3,-9])
np.cov(target1, target2)

array([[ 11.66666667, -16.66666667],
       [-16.66666667,  38.66666667]])

np.corrcoef(target1,target2)

array([[ 1.        , -0.78470603],
       [-0.78470603,  1.        ]])

最后，需要说明二维 Numpy 数组中统计函数的 axis 参数，它能够进行某一个维度下的统计特征计算，当axis=0 时结果为列的统计指标，当 axis=1 时结果为行的统计指标：

target = np.arange(1,10).reshape(3,-1)
target

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

target.sum(0)

array([12, 15, 18])

target.sum(1)

array([ 6, 15, 24])

广播机制

广播机制用于处理两个不同维度数组之间的操作，这里只讨论不超过两维的数组广播机制。

标量和数组的操作

当一个标量和数组进行运算时，标量会自动把大小扩充为数组大小，之后进行逐元素操作：

res = 3 * np.ones((2,2)) + 1
res

array([[4., 4.],
       [4., 4.]])

res = 1 / res
res

array([[0.25, 0.25],
       [0.25, 0.25]])

二维数组之间的操作

• 维度匹配或第一组行列中一个匹配、另一个为1，则可进行矩阵运算。

当两个数组维度完全一致时，使用对应元素的操作，否则会报错，除非其中的某个数组的维度是 m × 1 或者
1 × n ，那么会扩充其具有 1 的维度为另一个数组对应维度的大小。例如， 1 × 2 数组和 3 × 2 数组做逐元素
运算时会把第一个数组扩充为 3 × 2 ，扩充时的对应数值进行赋值。但是，需要注意的是，如果第一个数组
的维度是 1 × 3 ，那么由于在第二维上的大小不匹配且不为 1 ，此时报错。

res = np.ones((3,2))
res

array([[1., 1.],
       [1., 1.],
       [1., 1.]])

res * np.array([[2,3]]) # 扩充第一维度为 3

array([[2., 3.],
       [2., 3.],
       [2., 3.]])

res * np.array([[2],[3],[4]]) # 扩充第二维度为 2

array([[2., 2.],
       [3., 3.],
       [4., 4.]])

 res * np.array([[2]]) # 等价于两次扩充

array([[2., 2.],
       [2., 2.],
       [2., 2.]])

一维数组与二维数组的操作

当一维数组 Ak 与二维数组 Bm;n 操作时，等价于把一维数组视作 A1;k 的二维数组，使用的广播法则与【 b】
中一致，当 k! = n 且 k; n 都不是 1 时报错。

np.ones(3) + np.ones((2,3))

array([[2., 2., 2.],
       [2., 2., 2.]])

np.ones(3) + np.ones((2,1))

array([[2., 2., 2.],
       [2., 2., 2.]])

np.ones(1) + np.ones((2,3))

array([[2., 2., 2.],
       [2., 2., 2.]])

向量与矩阵的计算

向量内积： dot

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-H4XKtZWC-1608129754976)(attachment:image.png)]

a = np.array([1,2,3])
b = np.array([1,3,5])
a.dot(b)

22

向量范数和矩阵范数： np.linalg.norm

在矩阵范数的计算中，最重要的是 ord 参数，可选值如下：

ord（取值1，2，np.inf分别表示1范式，2范式，无穷范数）

martix_target = np.arange(4).reshape(-1,2)## reshape中可以设定列为2，则行无需设定，只要定为-1即可自动设置
martix_target

array([[0, 1],
       [2, 3]])

np.linalg.norm(martix_target, 'fro') #linalg=linear（线性）+algebra（代数），norm则表示范数。

3.7416573867739413

np.linalg.norm(martix_target, np.inf)

5.0

np.linalg.norm(martix_target, 2)

3.702459173643833

 vector_target = np.arange(4)
vector_target

array([0, 1, 2, 3])

np.linalg.norm(vector_target, np.inf)

3.0

 np.linalg.norm(vector_target, 2)

3.7416573867739413

np.linalg.norm(vector_target, 3)

3.3019272488946263

矩阵乘法： @

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zs0JqlTs-1608129754981)(attachment:image.png)]

a = np.arange(4).reshape(-1,2)
a

array([[0, 1],
       [2, 3]])

b = np.arange(-4,0).reshape(-1,2)
b

array([[-4, -3],
       [-2, -1]])

a@b

array([[ -2,  -1],
       [-14,  -9]])

练习

Ex1：利用列表推导式写矩阵乘法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-v4mzJOvj-1608129754982)(attachment:image.png)]

M1=np.random.rand(2,3)
M2 = np.random.rand(3,4)

res=np.empty((M1.shape[0],M2.shape[1]))

array([[0.00000000e+000, 0.00000000e+000, 0.00000000e+000,
        0.00000000e+000],
       [0.00000000e+000, 5.84973725e-321, 7.23188049e-308,
        7.56525112e-307]])

[M1[i][k] * M2[k][j] for i in range(M1.shape[0])for j in range(M2.shape[1])for k in range(M1.shape[1])]
((M1@M2 - res) < 1e-15).all()

True

Ex2：更新矩阵

A=np.arange(9).reshape(3,3)+1
A

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

B=np.array([A[i][j]*sum(1/A[i][:])for i in np.arange(3) for j in np.arange(3)]).reshape(3,3)
B

array([[1.83333333, 3.66666667, 5.5       ],
       [2.46666667, 3.08333333, 3.7       ],
       [2.65277778, 3.03174603, 3.41071429]])

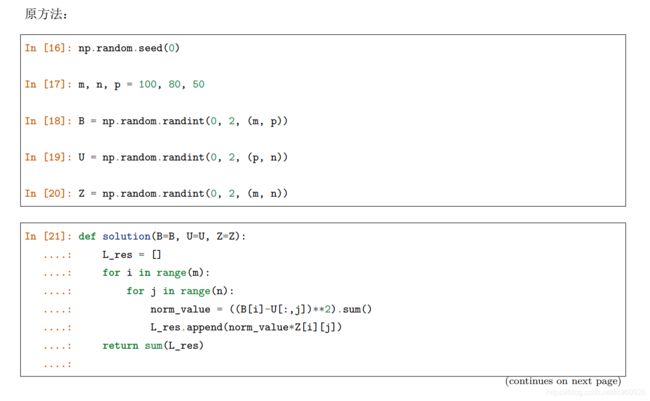
Ex3：卡方统计量

组长教我截图，我就学了，做到第二题做不下去了。

Ex4：改进矩阵计算的性能

Ex5：连续整数的最大长度

输入一个整数的 Numpy 数组，返回其中递增连续整数子数组的最大长度。例如，输入 [1,2,5,6,7]， [5,6,7] 为
具有最大长度的递增连续整数子数组，因此输出 3；输入 [3,2,1,2,3,4,6]， [1,2,3,4] 为具有最大长度的递增连
续整数子数组，因此输出 4。请充分利用 Numpy 的内置函数完成。（提示：考虑使用 nonzero, diff 函数）