马尔可夫决策过程(Markov Decision Process)学习笔记
Markov Decision Process学习笔记
- 马尔可夫决策过程(Markov Decision Process)学习笔记
-
- 1. 基本的概率定义
- 2. 如何理解状态 S S S和动作 A A A
- 3. 策略和价值函数
- 4. 价值函数的贝尔曼方程
-
- 4.1 何为贝尔曼方程
- 4.2 状态价值函数的贝尔曼方程
- 4.3 动作价值函数贝尔曼方程
- 4.4 回溯图理解法
-
- 4.4.1 状态价值函数回溯图分解如下
- 4.4.2 动作价值函数的回溯图分解如下
- 4.5 实例理解法
- 5. 最优策略和最优价值函数
-
- 5.1 实例理解
- 参考
马尔可夫决策过程(Markov Decision Process)学习笔记
1. 基本的概率定义
-
马尔可夫性质表示下一刻的状态只与当前时刻状态有关,其他的历史信息可以丢弃不用。因为该状态已经是未来的充分统计。
P ( s t + 1 ∣ s t ) = P ( s t + 1 ∣ s t , s t − 1 , ⋯ , s 0 ) P(s_{t+1}{\mid}s_t) = P(s_{t+1}{\mid}s_t, s_{t-1},\cdots,s_0) P(st+1∣st)=P(st+1∣st,st−1,⋯,s0) -
在给定前继状态和动作的值时, s ′ , s ∈ S , r ∈ R s^{\prime}, s \in \mathcal{S}, r \in \mathcal{R} s′,s∈S,r∈R,在t时刻发生这些值的概率,这定义了MDP环境的动态特性。
p ( s ′ , r ∣ s , a ) ≐ Pr { S t = s ′ , R t = r ∣ S t − 1 = s , A t − 1 = a } (1) p\left(s^{\prime}, r \mid s, a\right) \doteq \operatorname{Pr}\left\{S_{t}=s^{\prime}, R_{t}=r \mid S_{t-1}=s, A_{t-1}=a\right\} \tag{1} p(s′,r∣s,a)≐Pr{St=s′,Rt=r∣St−1=s,At−1=a}(1)
其中:
∑ s ′ ∈ S ∑ r ∈ R p ( s ′ , r ∣ s , a ) = 1 , for all s ∈ S , a ∈ A ( s ) \sum_{s^{\prime} \in \mathcal{S}} \sum_{r \in \mathcal{R}} p\left(s^{\prime}, r \mid s, a\right)=1, \text { for all } s \in \mathcal{S}, a \in \mathcal{A}(s) s′∈S∑r∈R∑p(s′,r∣s,a)=1, for all s∈S,a∈A(s) -
状态转移概率,这是一个三参数函数 p : S × S × A → [ 0 , 1 ] p: \mathcal{S} \times \mathcal{S} \times \mathcal{A} \rightarrow[0,1] p:S×S×A→[0,1],这里面不包含受益 r r r,注意和上面表达的区别和联系。
P s s ′ a ≐ p ( s ′ ∣ s , a ) ≐ Pr { S t = s ′ ∣ S t − 1 = s , A t − 1 = a } = ∑ r ∈ R p ( s ′ , r ∣ s , a ) (2) \mathcal{P}_{s s^{\prime}}^{a} \doteq p\left(s^{\prime} \mid s, a\right) \doteq \operatorname{Pr}\left\{S_{t}=s^{\prime} \mid S_{t-1}=s, A_{t-1}=a\right\}=\sum_{r \in \mathcal{R}} p\left(s^{\prime}, r \mid s, a\right) \tag{2} Pss′a≐p(s′∣s,a)≐Pr{St=s′∣St−1=s,At−1=a}=r∈R∑p(s′,r∣s,a)(2) -
“状态-动作”二元组的期望收益, r : S × A → R r: \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R} r:S×A→R:
R s a ≐ r ( s , a ) ≐ E [ R t ∣ S t − 1 = s , A t − 1 = a ] = ∑ r ∈ R r ∑ s ′ ∈ S p ( s ′ , r ∣ s , a ) (3) \mathcal{R}_{s}^{a} \doteq r(s, a) \doteq \mathbb{E}\left[R_{t} \mid S_{t-1}=s, A_{t-1}=a\right]\\ \\=\sum_{r \in \mathcal{R}} r \sum_{s^{\prime} \in \mathcal{S}} p\left(s^{\prime}, r \mid s, a\right) \tag{3} Rsa≐r(s,a)≐E[Rt∣St−1=s,At−1=a]=r∈R∑rs′∈S∑p(s′,r∣s,a)(3)
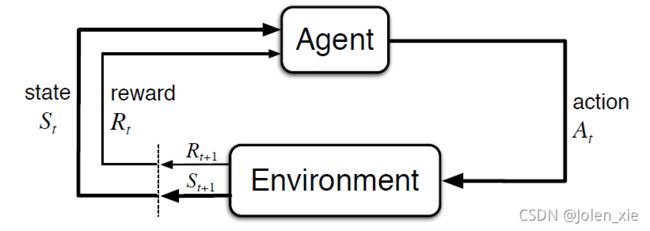
2. 如何理解状态 S S S和动作 A A A
动作可以是任何我们想要做的策略
状态则可以是任何有所帮助的事情
3. 策略和价值函数
- 价值函数是状态(或状态与动作二元组)的函数,用来评估当前智能体在给定状态(或给定状态与动作)下有多好(回报的期望值)。
- 策略是从状态到每个动作的选择概率之间的映射
- 策略 π \pi π 下状态 s s s的价值函数记为 v π ( s ) v_{\pi}(s) vπ(s),也称为状态价值函数,即从状态 s s s开始,智能体按照策略 π \pi π 进行决策所获得的回报的概率期望值。
v π ( s ) ≐ E π [ G t ∣ S t = s ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s ] , for all s ∈ S (4) v_{\pi}(s) \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right]=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s\right], \text { for all } s \in \mathcal{S} \tag{4} vπ(s)≐Eπ[Gt∣St=s]=Eπ[k=0∑∞γkRt+k+1∣St=s], for all s∈S(4) - 策略 π \pi π 下在状态 s s s时采取动作 a a a的价值记为 q π ( s , a ) q_{\pi}(s, a) qπ(s,a),也称为动作价值函数。这就是根据策略 π \pi π ,从状态 s s s开始,执行动作 a a a之后,所有可能的决策序列的期望回报
q π ( s , a ) ≐ E π [ G t ∣ S t = s , A t = a ] = E π [ ∑ k = 0 ∞ γ k R t + k + 1 ∣ S t = s , A t = a ] (5) q_{\pi}(s, a) \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right]=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s, A_{t}=a\right] \tag{5} qπ(s,a)≐Eπ[Gt∣St=s,At=a]=Eπ[k=0∑∞γkRt+k+1∣St=s,At=a](5)
4. 价值函数的贝尔曼方程
4.1 何为贝尔曼方程
贝尔曼方程(Bellman Equation)也被称作动态规划方程(Dynamic Programming Equation),是动态规划(Dynamic Programming)这些数学最佳化方法能够达到最佳化的必要条件(来自百度百科,Wikipedia)。
4.2 状态价值函数的贝尔曼方程
v π ( s ) ≐ E π [ G t ∣ S t = s ] = E π [ R t + 1 + γ G t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) [ r + γ E π [ G t + 1 ∣ S t + 1 = s ′ ] ] = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] , for all s ∈ S , (6) \begin{aligned} v_{\pi}(s) & \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right] \\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s\right] \\ &=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \mathbb{E}_{\pi}\left[G_{t+1} \mid S_{t+1}=s^{\prime}\right]\right] \\ &=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right], \quad \text { for all } s \in \mathcal{S}, \end{aligned} \tag{6} vπ(s)≐Eπ[Gt∣St=s]=Eπ[Rt+1+γGt+1∣St=s]=a∑π(a∣s)s′∑r∑p(s′,r∣s,a)[r+γEπ[Gt+1∣St+1=s′]]=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)], for all s∈S,(6)
该等式表达了状态价值和后继状态价值之间的关系,对所有可能性采用其出现概率进行了加权平均。
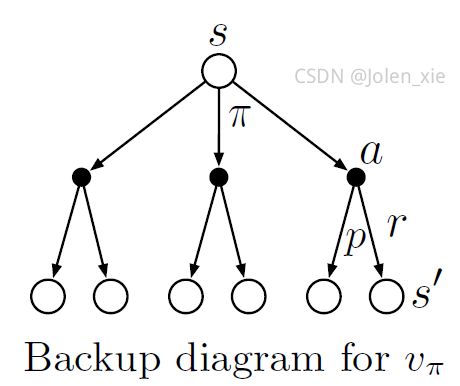
解析:
配合上面的状态价值回溯图理解上面式(6),在式(6)中第三行中的 ∑ a π ( a ∣ s ) ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) \sum_{a} \pi(a \mid s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right) ∑aπ(a∣s)∑s′∑rp(s′,r∣s,a) 表示第一行中的 E π [ ∗ ∣ S t = s ] \mathbb{E}_{\pi}\left[* \mid S_{t}=s\right] Eπ[∗∣St=s]变量 G t G_t Gt的概率。 ∑ a π ( a ∣ s ) \sum_{a} \pi(a \mid s) ∑aπ(a∣s)遍历了策略 π \pi π在状态 s s s时所有可以选择行动;对于每一个可以选择的行动 a a a, ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right) ∑s′∑rp(s′,r∣s,a)遍历了所有可能到达的下一个状态 s ′ s^{\prime} s′,以及每个 s ′ s^{\prime} s′下所有可能得到的受益 r r r。这样就相当于遍历了未来所有可能情况(动作-下一状态-收益)的概率,以此对未来回报进行加权求和,作为状态 s s s的价值。
式(6)中第三行中的 E π [ G t + 1 ∣ S t + 1 = s ′ ] \mathbb{E}_{\pi}\left[G_{t+1} \mid S_{t+1}=s^{\prime}\right] Eπ[Gt+1∣St+1=s′]实际上就是 s ′ s^{\prime} s′的状态价值,故可以写成第四行的形式。虽然按照式(4)的定义, s ′ s^{\prime} s′的状态价值为 E π [ G t ∣ S t = s ] \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right] Eπ[Gt∣St=s],但这里 t + 1 t+1 t+1和 t t t并不会导致什么不同,因为策略和 p ( s ′ , r ∣ s , a ) p\left(s^{\prime}, r \mid s, a\right) p(s′,r∣s,a)都与 t t t无关。
4.3 动作价值函数贝尔曼方程
q π ( s , a ) ≐ E π [ G t ∣ S t = s , A t = a ] = E π [ R t + 1 + γ G t + 1 ∣ S t = s , A t = a ] = ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) [ r + γ ∑ a ′ π ( a ′ ∣ s ′ ) E π [ G t + 1 ∣ S t + 1 = s ′ , A t + 1 = a ′ ] ] = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ ∑ a ′ π ( a ′ ∣ s ′ ) q π ( s ′ , a ′ ) ] = R s a + γ ∑ s ′ ∈ S P s s ′ a ∑ a ′ ∈ A π ( a ′ ∣ s ′ ) q π ( s ′ , a ′ ) (7) \begin{aligned} q_{\pi}(s, a) &\doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right] \\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s, A_{t}=a\right]\\ &= \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \sum_{a^{\prime}} \pi(a^{\prime} \mid s^{\prime})\mathbb{E}_{\pi}\left[G_{t+1} \mid S_{t+1}=s^{\prime},A_{t+1}=a^{\prime}\right]\right] \\ &=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \sum_{a^{\prime}} \pi(a^{\prime} \mid s^{\prime}) q_{\pi}(s^{\prime}, a^{\prime}) \right]\\ &= \mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} \sum_{a^{\prime} \in \mathcal{A}} \pi\left(a^{\prime} \mid s^{\prime}\right) q_{\pi}\left(s^{\prime}, a^{\prime}\right) \end{aligned} \tag{7} qπ(s,a)≐Eπ[Gt∣St=s,At=a]=Eπ[Rt+1+γGt+1∣St=s,At=a]=s′∑r∑p(s′,r∣s,a)[r+γa′∑π(a′∣s′)Eπ[Gt+1∣St+1=s′,At+1=a′]]=s′,r∑p(s′,r∣s,a)[r+γa′∑π(a′∣s′)qπ(s′,a′)]=Rsa+γs′∈S∑Pss′aa′∈A∑π(a′∣s′)qπ(s′,a′)(7)
注意式(7)中没有出现式(6)的 ∑ a π ( a ∣ s ) \sum_{a} \pi(a \mid s) ∑aπ(a∣s),因为在动作价值函数中,动作时参数之一,是已经确定的,因此他的根节点只有唯一的一个。第三行引入 a ′ a^{\prime} a′为下一时刻的动作,这是为了与 s ′ s^{\prime} s′组成“状态-动作”二元组,以构造动作价值函数的形式,在第四行引入 q π ( s ′ , a ′ ) q_{\pi}\left(s^{\prime},a^{\prime}\right) qπ(s′,a′)。然后第五行可以根据式(2)(3)简化。
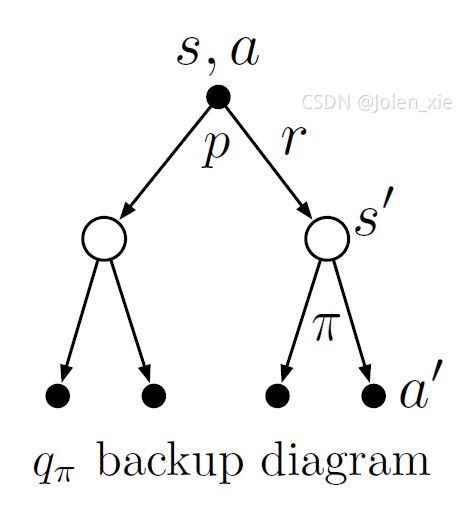
解析:
配合上面的动作价值回溯图理解式(7),在式(7)中第三行 ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right) ∑s′∑rp(s′,r∣s,a)是对 E π [ ∗ ∣ S t = s , A ( t ) = a ] \mathbb{E}_{\pi}\left[* \mid S_{t}=s, A_(t)=a\right] Eπ[∗∣St=s,A(t)=a]的变量 R t + 1 R_{t+1} Rt+1的概率,遍历了根节点分支中所有的状态和奖励,这里得出了奖励的期望,如式(3)。 ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) ∑ a ′ π ( a ′ ∣ s ′ ) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\sum_{a^{\prime}} \pi\left(a^{\prime} \mid s^{\prime}\right) ∑s′∑rp(s′,r∣s,a)∑a′π(a′∣s′)是 G t + 1 G_{t+1} Gt+1的概率,遍历了根节点分支中所有状态以及其可能做出的所有的动作。
4.4 回溯图理解法
4.4.1 状态价值函数回溯图分解如下
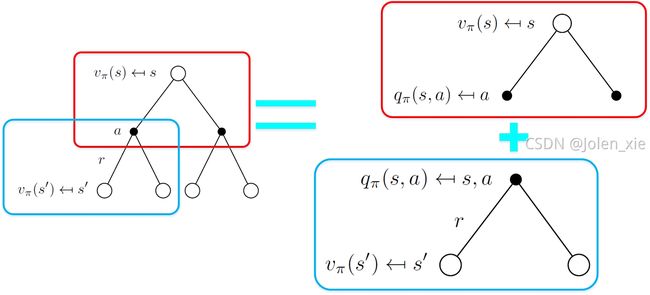
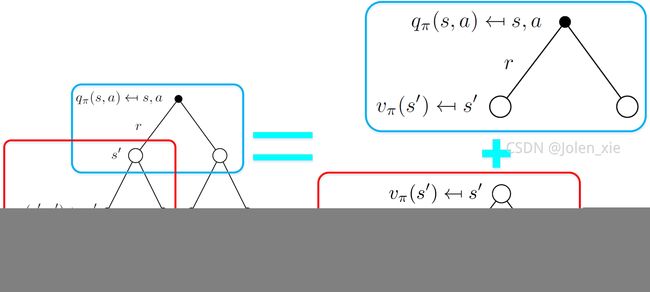
把状态价值回溯图分解成两个部分,红色部分是根节点 v π ( s ) v_{\pi}(s) vπ(s)与策略 π \pi π下所有动作组成的可执行状态-动作二元组,首先列出这一层的回溯方程:
v π ( s ) = π ( a 1 ∣ s ) q π ( s , a 1 ) + π ( a 2 ∣ s ) q π ( s , a 2 ) + ⋯ = ∑ a π ( a ∣ s ) q π ( s , a ) (8) \begin{aligned} v_{\pi}(s) &= \pi(a_1 {\mid} s)q_{\pi}(s,a_1)+ \pi(a_2 {\mid} s)q_{\pi}(s,a_2)+\cdots\\ &=\sum_{a}\pi(a {\mid} s)q_{\pi}(s,a) \end{aligned}\tag{8} vπ(s)=π(a1∣s)qπ(s,a1)+π(a2∣s)qπ(s,a2)+⋯=a∑π(a∣s)qπ(s,a)(8)
红色部分是根节点为 q π ( s , a ) q_{\pi}(s,a) qπ(s,a)与特定动作 a a a与其MDP环境动态特性 p ( s ′ , r ∣ s , a ) p\left(s^{\prime}, r \mid s, a\right) p(s′,r∣s,a)下所有可能的 v π ( s ) v_{\pi}(s) vπ(s)叶子节点,列出第二层的回溯方程:
q π ( s , a ) = p ( s 1 ′ , r 1 ∣ s , a ) ( r 1 + γ v π ( s 1 ′ ) ) + p ( s 2 ′ , r 2 ∣ s , a ) ( r 2 + γ v π ( s 2 ′ ) ) + ⋯ = ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) ( r + γ v π ( s ′ ) ) (9) \begin{aligned} q_{\pi}(s,a)&=p\left(s^{\prime}_1, r_1 \mid s, a\right)(r_1+\gamma v_{\pi}(s^{\prime}_1) )+p\left(s^{\prime}_2, r_2 \mid s, a\right)(r_2+\gamma v_{\pi}(s^{\prime}_2) )+\cdots\\ &=\sum_{s^{\prime}}\sum_{r}p\left(s^{\prime}, r \mid s, a\right)(r+\gamma v_{\pi}(s^{\prime})) \end{aligned}\tag{9} qπ(s,a)=p(s1′,r1∣s,a)(r1+γvπ(s1′))+p(s2′,r2∣s,a)(r2+γvπ(s2′))+⋯=s′∑r∑p(s′,r∣s,a)(r+γvπ(s′))(9)
因此,把式(9)代入式(8)可以得到:
v π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] , for all s ∈ S v_{\pi}(s)=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right], \quad \text { for all } s \in \mathcal{S} vπ(s)=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)], for all s∈S
4.4.2 动作价值函数的回溯图分解如下
把式(8)代入式(9)可以得到(这里的式(8)(9)的符号的角标需要根据上面回溯图修改)
q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ ∑ a ′ π ( a ′ ∣ s ′ ) q π ( s ′ , a ′ ) ] q_{\pi}(s,a)=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \sum_{a^{\prime}} \pi(a^{\prime} \mid s^{\prime}) q_{\pi}(s^{\prime}, a^{\prime}) \right]\\ qπ(s,a)=s′,r∑p(s′,r∣s,a)[r+γa′∑π(a′∣s′)qπ(s′,a′)]
4.5 实例理解法
举例来说,假设智能体在一个如图 1 所示的 2×2 网格中移动,智能体在每个格子(状态)中都可以选择向上、下、左、右四个方向移动(动作),移出网格的动作会使智能体停留在原地。智能体从其他格子移动到 B,或者从在 B 中选择向上或向左移动停留在 B,都会获得 +5 的收益,其他动作的收益均为 0。

由式 (6),可以定义状态 A A A在策略 π \pi π下的状态价值函数为
v π ( A ) ≐ E π [ G t ∣ S t = A ] v_{\pi}(A) \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=A\right] vπ(A)≐Eπ[Gt∣St=A]
令 γ = 0.7 \gamma = 0.7 γ=0.7,状态 A A A的价值函数可以写成
v π ( A ) = ∑ a π ( a ∣ s ) ( r + 0.7 v π ( s ′ ) ) (10) v_{\pi}(A)=\sum_{a} \pi(a \mid s)\left(r+0.7 v_{\pi}\left(s^{\prime}\right)\right) \tag{10} vπ(A)=a∑π(a∣s)(r+0.7vπ(s′))(10)
上式中 ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right) ∑s′∑rp(s′,r∣s,a)的值是确定为1的,因为定义了上、下、左、右只能百分之百前往准确的一个状态,不会有概率去往其他的状态。因此在执行动作 a a a后只有唯一的一个状态 s ′ s^{\prime} s′和收益 r r r。虽然省略了像(6)式中那样对 s ′ s^{\prime} s′和 r r r进行求和,但 s ′ s^{\prime} s′和受益 r r r的值仍然依赖于选择的动作 a a a。
假设智能体在每个状态都随机地选择动作,即选择选择向上、下、左、右四个方向移动的概率均为0.25,则由式(10),有
v π ( A ) = 1 4 ( 5 + 0.7 v π ( B ) ) + 1 4 ( 0 + 0.7 v π ( C ) ) + 1 4 ( 0 + 0.7 v π ( A ) ) + 1 4 ( 0 + 0.7 v π ( A ) ) (11) v_{\pi}(A)=\frac{1}{4}\left(5+0.7 v_{\pi}(B)\right)+\frac{1}{4}\left(0+0.7 v_{\pi}(C)\right)+\frac{1}{4}\left(0+0.7 v_{\pi}(A)\right)+\frac{1}{4}\left(0+0.7 v_{\pi}(A)\right)\tag{11} vπ(A)=41(5+0.7vπ(B))+41(0+0.7vπ(C))+41(0+0.7vπ(A))+41(0+0.7vπ(A))(11)
式(11)中等号右边的四项分别为在状态 A A A选择向右、下、左、上移动所带来的收益。类似地,可以得到状态 B , C , D B, C, D B,C,D的状态价值,组成方程组
v π ( A ) = 1 2 0.7 v π ( A ) + 1 4 ( 5 + 0.7 v π ( B ) ) + 1 4 0.7 v π ( C ) v π ( B ) = 1 2 ( 5 + 0.7 v π ( B ) ) + 1 4 0.7 v π ( A ) + 1 4 0.7 v π ( D ) v π ( C ) = 1 2 0.7 v π ( C ) + 1 4 0.7 v π ( A ) + 1 4 0.7 v π ( D ) v π ( D ) = 1 2 0.7 v π ( D ) + 1 4 ( 5 + 0.7 v π ( B ) ) + 1 4 0.7 v π ( C ) \begin{array}{lll} v_{\pi}(A) & =\frac{1}{2} 0.7 v_{\pi}(A) & +\frac{1}{4}\left(5+0.7 v_{\pi}(B)\right) & +\frac{1}{4} 0.7 v_{\pi}(C) \\\\ v_{\pi}(B) & =\frac{1}{2}\left(5+0.7 v_{\pi}(B)\right) \quad & +\frac{1}{4} 0.7 v_{\pi}(A) & +\frac{1}{4} 0.7 v_{\pi}(D) \\\\ v_{\pi}(C) & =\frac{1}{2} 0.7 v_{\pi}(C) & +\frac{1}{4} 0.7 v_{\pi}(A) & +\frac{1}{4} 0.7 v_{\pi}(D) \\\\ v_{\pi}(D) & =\frac{1}{2} 0.7 v_{\pi}(D) & +\frac{1}{4}\left(5+0.7 v_{\pi}(B)\right) & +\frac{1}{4} 0.7 v_{\pi}(C) \end{array} vπ(A)vπ(B)vπ(C)vπ(D)=210.7vπ(A)=21(5+0.7vπ(B))=210.7vπ(C)=210.7vπ(D)+41(5+0.7vπ(B))+410.7vπ(A)+410.7vπ(A)+41(5+0.7vπ(B))+410.7vπ(C)+410.7vπ(D)+410.7vπ(D)+410.7vπ(C)
上面的方程组有唯一解
v π ( A ) = 4.17 v π ( B ) = 6.09 v π ( C ) = 2.24 v π ( D ) = 4.17 \begin{aligned} &v_{\pi}(A)=4.17 \\ &v_{\pi}(B)=6.09 \\ &v_{\pi}(C)=2.24 \\ &v_{\pi}(D)=4.17 \end{aligned} vπ(A)=4.17vπ(B)=6.09vπ(C)=2.24vπ(D)=4.17
虽然状态价值函数的定义中包含了未来所有可能的收益,但通过贝尔曼方程,就能以求解线性方程组的方式,计算得到了各个状态的价值。
5. 最优策略和最优价值函数
解决一个强化学习任务就意味着要找出一个策略,使其能够在长期过程中获得大量受益。对于有限MDP,我们可以通过比较价值函数精确地定义一个最优策略。若对于所有的 s ∈ S s \in \mathcal{S} s∈S, π ≥ π ′ \pi \geq \pi^{\prime} π≥π′,那么应当 v π ( s ) ≥ v π ′ ( s ) v_{\pi}(s) \geq v_{\pi^{\prime}}(s) vπ(s)≥vπ′(s)。总会存在至少一个策略不劣于其他所有的策略,这就是最优策略。最优状态价值函数记为 v ∗ ( s ) v_{*}(s) v∗(s),其定义为:对于任意 s ∈ S s \in \mathcal{S} s∈S,
v ∗ ( s ) ≐ max π v π ( s ) , for all s ∈ S v_{*}(s) \doteq \max _{\pi} v_{\pi}(s), \text{ for all } s \in \mathcal{S} v∗(s)≐πmaxvπ(s), for all s∈S
最优动作价值函数记为 q ∗ ( s , a ) q_{*}(s, a) q∗(s,a),其定义为:对于任意 s ∈ S s \in \mathcal{S} s∈S, a ∈ A ( s ) a \in \mathcal{A}(s) a∈A(s),
q ∗ ( s , a ) ≐ max π q π ( s , a ) for all s ∈ S , a ∈ A ( s ) q_{*}(s, a) \doteq \max _{\pi} q_{\pi}(s, a) \text{ for all } s \in \mathcal{S},a \in \mathcal{A}(s) q∗(s,a)≐πmaxqπ(s,a) for all s∈S,a∈A(s)
对于“状态-动作”二元组 ( s , a ) (s,a) (s,a),这个函数给出了在状态 s s s下,先采取动作 a a a,之后按照最优策略去决策的期望回报。因此,我们可以用 v ∗ v_{*} v∗来表示 q ∗ q_{*} q∗
q ∗ ( s , a ) = E [ R t + 1 + γ v ∗ ( S t + 1 ) ∣ S t = s , A t = a ] q_{*}(s, a)=\mathbb{E}\left[R_{t+1}+\gamma v_{*}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] q∗(s,a)=E[Rt+1+γv∗(St+1)∣St=s,At=a]
贝尔曼最优方程阐述了一个事实:最优策略下各个状态的价值一定等于这个状态下最优动作的期望回报
v ∗ ( s ) = max a ∈ A ( s ) q π ∗ ( s , a ) = max a E π ∗ [ G t ∣ S t = s , A t = a ] = max a E π ∗ [ R t + 1 + γ G t + 1 ∣ S t = s , A t = a ] = max a E [ R t + 1 + γ v ∗ ( S t + 1 ) ∣ S t = s , A t = a ] = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v ∗ ( s ′ ) ] \begin{aligned} v_{*}(s) &=\max _{a \in \mathcal{A}(s)} q_{\pi_{*}}(s, a) \\ &=\max _{a} \mathbb{E}_{\pi_{*}}\left[G_{t} \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \mathbb{E}_{\pi_{*}}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{*}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{*}\left(s^{\prime}\right)\right] \end{aligned} v∗(s)=a∈A(s)maxqπ∗(s,a)=amaxEπ∗[Gt∣St=s,At=a]=amaxEπ∗[Rt+1+γGt+1∣St=s,At=a]=amaxE[Rt+1+γv∗(St+1)∣St=s,At=a]=amaxs′,r∑p(s′,r∣s,a)[r+γv∗(s′)]
最后两个等式就是 v ∗ v_{*} v∗的贝尔曼最优方程的两种形式。
q ∗ q_{*} q∗的贝尔曼最优方程如下
q ∗ ( s , a ) = E π ∗ [ R t + 1 + γ max a ′ q ∗ ( S t + 1 , a ′ ∣ ) S t = s , A t = a ] = ∑ s ′ , r p ( s ′ , r ∣ s , a ) ( r + γ max a ′ q ∗ ( s ′ , a ′ ) ) \begin{aligned} q_{*}(s,a) &=\mathbb{E}_{\pi_{*}} \left[R_{t+1} + \gamma \max_{a^{\prime}}q_{*}(S_{t+1},a^{\prime}{\mid})S_t=s,A_t=a \right] \\ &=\sum_{s^{\prime},r}p\left(s^{\prime}, r \mid s, a\right)(r+\gamma \max_{a^{\prime}}q_{*}(s^{\prime},a^{\prime})) \end{aligned} q∗(s,a)=Eπ∗[Rt+1+γa′maxq∗(St+1,a′∣)St=s,At=a]=s′,r∑p(s′,r∣s,a)(r+γa′maxq∗(s′,a′))
对于最优价值函数 v ∗ v_{*} v∗来说,任何贪心策略都是最优策略。
π ∗ ( a ∣ s ) = { 1 if a = arg max a ∈ A q ∗ ( s , a ) 0 otherwise \pi_{*}(a{\mid}s) = \left \{ \begin{aligned} 1 &\text{ if } a = \argmax_{a\in A}q_{*}(s,a)\\ 0 &\text{ otherwise} \end{aligned} \right. π∗(a∣s)=⎩⎨⎧10 if a=a∈Aargmaxq∗(s,a) otherwise
5.1 实例理解
下面这个图是一个持续性MDP,在顶部状态下,可选的动作只有left和right。线上的数值表示在做每一个动作后获得的固定收益。我们有两个确定的策略 π l e f t \pi_{left} πleft和 π r i g h t \pi_{right} πright。在 γ \gamma γ分别为0、0.9、0.5时,哪个策略是最优的?
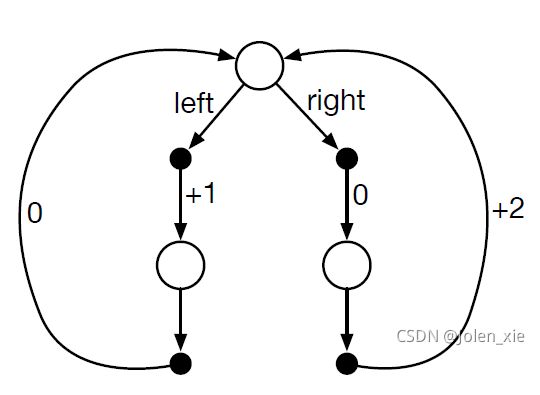
从上面的回溯图中可以看出,每个动作可选择的状态都是唯一的,因此 p ( s ′ , r ∣ s , a ) = 1 p\left(s^{\prime}, r \mid s, a\right)=1 p(s′,r∣s,a)=1,在指定策略 π \pi π下可以得
v π ( s t ) = r + γ v π ( s t + 1 ) = ∑ t = 0 ∞ γ t r t \begin{aligned} v_{\pi}(s_t)&=r+\gamma v_{\pi}(s_{t+1})\\ &=\sum_{t=0}^{\infty}\gamma^{t}r_t \end{aligned} vπ(st)=r+γvπ(st+1)=t=0∑∞γtrt
因此,当 γ = 0 \gamma=0 γ=0,则状态价值函数只与当前的受益有关,与为了受益无关
v π left = 1 v π right = 0 v_{\pi_\text{left}}=1\\ v_{\pi_\text{right}}=0 vπleft=1vπright=0
此刻策略 π left \pi_\text{left} πleft是最优策略。
当 γ = 0.9 \gamma=0.9 γ=0.9时,
v π left = 1 + 0.9 ∗ 0 + 0. 9 2 ∗ 1 + ⋯ = ∑ k = 0 ∞ 0. 9 2 k = 1 1 − 0. 9 2 ≈ 5.3 v π right = 0 + 0.9 ∗ 2 + 0. 9 2 ∗ 0 + ⋯ = ∑ k = 0 ∞ 0. 9 2 k + 1 ∗ 2 = 0.9 1 − 0. 9 2 ∗ 2 ≈ 9.5 v_{\pi_\text{left}}=1+0.9*0+0.9^2*1+\cdots =\sum_{k=0}^{\infty}0.9^{2k}=\frac{1}{1-0.9^2}\approx5.3\\ v_{\pi_\text{right}}=0+0.9*2+0.9^2*0+\cdots=\sum_{k=0}^{\infty}0.9^{2k+1}*2=\frac{0.9}{1-0.9^2}*2\approx9.5 vπleft=1+0.9∗0+0.92∗1+⋯=k=0∑∞0.92k=1−0.921≈5.3vπright=0+0.9∗2+0.92∗0+⋯=k=0∑∞0.92k+1∗2=1−0.920.9∗2≈9.5
此刻策略 π right \pi_\text{right} πright是最优策略。
当 γ = 0.5 \gamma=0.5 γ=0.5时,
v π left = 1 + 0.5 ∗ 0 + 0. 5 2 ∗ 1 + ⋯ = ∑ k = 0 ∞ 0. 5 2 k = 1 1 − 0. 5 2 ≈ 1.3 v π right = 0 + 0.5 ∗ 2 + 0. 5 2 ∗ 0 + ⋯ = ∑ k = 0 ∞ 0. 5 2 k + 1 ∗ 2 = 0.5 1 − 0. 5 2 ∗ 2 ≈ 1.3 v_{\pi_\text{left}}=1+0.5*0+0.5^2*1+\cdots =\sum_{k=0}^{\infty}0.5^{2k}=\frac{1}{1-0.5^2}\approx1.3\\ v_{\pi_\text{right}}=0+0.5*2+0.5^2*0+\cdots=\sum_{k=0}^{\infty}0.5^{2k+1}*2=\frac{0.5}{1-0.5^2}*2\approx1.3 vπleft=1+0.5∗0+0.52∗1+⋯=k=0∑∞0.52k=1−0.521≈1.3vπright=0+0.5∗2+0.52∗0+⋯=k=0∑∞0.52k+1∗2=1−0.520.5∗2≈1.3
此刻策略 π right \pi_\text{right} πright, π left \pi_\text{left} πleft都为最优的策略。
参考
[1] Reinforcement Learning: An Introduction second edition
[2] Videos of David Sliver [YouTube] [BiliBili]
[3] https://blog.nex3z.com/2019/10/17/rl-notes-bellman-equation/