[NAS]NSE:Evolving Search Space for Neural Architecture Search
基于搜索空间进化的神经网络架构搜索
- Abstract
- Section I Introduction
- Section II Related Work
-
- Part 1 NAS 算法设计
- Part 2 Search Space Design
- Section III Method
-
- Problem Formulation
- Part 1 Overview
- Part 2 Supernet Training
- Part 3 Search Space Evolution
- Section IV Experimental Results
-
- Part 1 Search Space FLOPs
- Part 2 FLOPs约束实验
- Part 3 Latency Constraint Results
- Part 4 Necessity of Search Space Evolution
- Section V Ablation study
-
- Part 1 Search Space Quality
- Part 2 Continual Convergence
- Part 3 Impact of Components
- Section VI Conclusions
Abstract
神经网络架构搜索是专家手动设计的替代方案,为了在搜索空间中找到最优结构人们提出了各种搜索方法。人们认为搜索空间越大搜索结果会更优,因为他们可能包含耕读可能的候选网络。本文则是观察到一种惊奇的现象,即一味地扩大搜索空间对现有的NAS算法,如DARTS,PeoxylessNAS,SPOA是有害的,这一违反常理的现象表明,扩大搜索空间并不那么容易做到,但目前这一问题研究的还比较少。
本文提出一种搜索空间进化算法——NSE,这是首个专门为大型搜索空间问题而设计的神经网络搜索方案,目前的方法大多需要手动设计一个较好的搜搜空间,本文的NSE旨在最小化人工在其中的必要性。
简要来说,NSE会从一个搜索空间自己开始,重复两个步骤来进化搜索空间:
(1)从搜索空间子集中搜索一个优化后的空间
;
(2)从大量未遍历到的操作池中重新填充这一自己。
通过引入一个可学习的多分支设置,本文进一步扩展了网络结构的灵活性,通过NSE算法,本文在Imagenet搜索到333M Flops的网络结构达到了77.3%的精度;当以延迟作为约束时搜索到的结果也比之前最优的移动端模型优秀,达到了77.9%的top-1精度。
Section I Introduction
NAS为自动搜索特定任务的网络结构提供了可能性,研究人员主要基于强化学习和进化算法来进行NAS搜索,此外基于权重共享的搜索算法可以大大降低搜索成本,也称为NAS主流算法之一。
除了搜索方法,NAS的另一个关键组成部分是搜索空间。随着NAS的进步,搜索空间的质量也逐渐提高,研究发现良好的搜索空间对许多任务的性能都有提升,因此越来越多的研究人员致力于基于先验知识选择合适的操作、以及如果在更小的操作集中进行搜索,通常将每一层中的候选操作数量限制在10个以内(不包含激活函数部分),但是这不可避免也需要借助专家知识。
自然就会考虑一个问题:我们能否构造一个巨大的搜索空间,是之前搜索空间的一个超集,可以从中获得更好的结果?如果答案是可行的,那么这种方法可以简单的通过构造一个巨大的搜索空间来解决搜索空间的设计问题。但是目前NAS文献中对这一问题的研究较少,以及也有部分研究表明简单的扩大搜索空间并不利于最终结果的提升。
本文通过提出一个搜索空间进化方案——NSE来实现较大搜索空间的搜索,并不直接使用一个超大的搜索空间,NSE会从一个大小合理的子集开始,逐渐优化、填充出整个搜索空间,如Fig1(b)所示,这是一个不断进化的搜索空间。
NSE会在保留过去知识的同时逐渐搜索额外的候选操作,整个搜索是一个迭代的过程来遍历未被选择的候选操作。以及在迭代过程中并不总是保持单一架构而是使用one-shot方法训练超网将在帕累托最优找到的所有架构结合起来得到最优的搜索空间,这一空间会继承到下一轮搜索。此外搜索过程总会选择CNN中新的操作,有可能对特定任务会很有效。为了搜索到更复杂的结构本文进一步提出多分支方案,这样可以拥有更多不同结构的网络。
与DARTS这种只允许选择一个操作相比,多分支方案允许网络自适应的选择多个操作,通过构造一个多分支方案的概率模型本文可以得到每个候选操作的适应度,不选择适应度低于一定阈值的操作,这样可以逐步降低搜索空间的复杂性,同时提高其他路径组合被选择的可能性。
本文在在ImageNet上开始了以FLOPs和延迟作为约束的实验,实验结果表明NSE下的NAS方案有效的在一个富有潜力的超大搜索空间进行搜索,确保在迭代过程中持续的性能增长,从而获得SOTA。
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第1张图片](http://img.e-com-net.com/image/info8/e90b0dc55cac4581a99aedf8124ccb8e.jpg)
本文的工作总结如下:
(1)本文提出的NSE是第一个针对大空间进行NAS搜索的方案,最小化了对搜索空间的设计,同时演化过程的继承属性可以保留之前搜索空间获得的知识,同时会在当前搜索空间汇总添加新的操作来改进这些知识。
(2)本文提出一种计算操作适应度的概率模型,这样可以简化多分支结构的搜索方案的复杂性,并且可以更好的学习剩余被选择操作的共享权值。
Section II Related Work
Part 1 NAS 算法设计
神经网络搜索算法对于找到优异的网络结构至关重要,主要基于强化学习、进化算法、权重共享和one-shot算法。贝叶斯算法会将NAS看做是一个超参数有啊的问题,可以搜索非固定长度的神经网络;基于进化的则是通过遗传算法来生成候选结构,也能获得性能优异的候选网络。基于权重共享的方法则是使用一个超网,不同子网会直接继承超网的权重;one-shot NAS则是基于超网来预测predictor。
本文的NSE会保证在一定搜索空间子集上以一种有效的方式来更新候选操作,并且继承先前搜索到的候选操作的知识。
近期也有部分工作采用知识蒸馏或权重修剪来提升性能,但是都与本文的方法是正交的,也就是与本文带来的增益是互不干扰的。
Part 2 Search Space Design
搜索空间对搜索结果有巨大影响,因此搜索空间的设计也至关重要。比如Zoph等人采用基于块和跳跃连接的搜索空间,后续很多工作都是基于此进行的;在不同的块搜索不同的操作同时还需要限制候选操作的数量,这样才能限制搜索空间的大小。越来越多的工作提出在搜索空间中加入新的候选操作或新的模块,如多分支单元、树结构、shuffle操作,SE模块和swish激活等。本文的NSE会不断进化出新的操作。
Section III Method
Problem Formulation
本文将整个搜索空间池表示为一个有向无环图(DAG),共L层,El代表可能的操作,如3x3卷积,池化,identity等。 本文也将多分支结构考虑在内,即每层会选择N个候选操作,g则表示门操作是否选择当前操作,因此可能的组合数目一共为2^N,N为本层可选的操作数目。那么搜索的目标就是通过搜搜空间子集的进化寻找性能最好的架构,同时空间会逐步扩大。
Part 1 Overview
Fig 2展示了搜索空间的演进过程。
Step 1:
搜索空间池A中采样出搜索空间子集As,这是通过对每一层随机采样K个候选操作来实现的。在实际应用中搜索空间子集比搜索空间池要小得多,这样就不会在一个很大的搜索空间内搜索,搜索算法处理起来也比较容易。
Step 2:训练超网和简化搜索空间,这两个步骤会迭代进行,比如某个操作的适应度低于某个设定的阈值,那么就会将其从搜索空间子集中移除。
Step 3:在As中采样并进行评估得到优化后的搜索空间。具体来说,采样的适应度是通过验证精度来获得帕累托front,将在帕累托前端的结构进行聚合得到优化后的搜索空间,,这是包含帕累托front所有结构的最小搜索空间。
Step 4:得到新的搜索空间As’,是As优化后和Ar补充子集的组合,这样确保每一层仍然有K个候选操作,已经遍历过的搜索空间就被排出在Ar之外,即同一层同样的操作不会被采样2次,这样在As中积累的知识也会被继承,这样重复步骤2迭代进行。当A中没有组否操作时循环结束,此时作为架构搜索的最终结果。
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第2张图片](http://img.e-com-net.com/image/info8/2836a9258b2c476db6e8b51d1403fe4d.jpg)
Part 2 Supernet Training
多分支的前向路径
对于输入X,单分支的输出表示为opn,是否选择该输出表示为gn,这是一个伯努利分布,K表示当前层一共K个候选操作。
权重更新
搜索到的子网会继承超网的权重,共享权重Was的优化表示为:
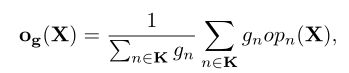
E是期望,Lce是交叉熵损失,采样到的子结构的优化目标是最小化期望值,利用随机梯度下降来更新响应的权值。超网需要被均匀的训练这样共享的权值才能较好的预测精度,因此本文采用伯努利-0,5采样每个可能的架构。
Part 3 Search Space Evolution
Fig 2中展示了搜索空间的进化步骤,下面详细介绍每一步。
Search Space simplification
本文采用的多分支方案将搜索空间扩大了90个数量级以上,为了更高效的寻找到最优架构本文提出在训练超网的同时逐步简化搜索空间自己。具体就是引入一个可学习的适应度指标来预测某个操作的适应度,并以此来指导搜索空间的简化详情参见Fig 3.
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第3张图片](http://img.e-com-net.com/image/info8/78eb73f105264311aaee9773d6993459.jpg)
Simplifying Search Space with Lock and Rehearse
第n路径其适应度指标θn如果低于一定阈值,就会将其从超网中删除。除了:
(1)该路径是reduction cell中的最后一条路径;
(2)该操作是从前一次迭代中继承过来的
这样才能确保被继承的知识不会被丢弃
本文将这种策略称之为L&R(Lock and Rehearse)
Probabilistic Modeling of Fitness Indicators
超网每迭代两次后更新一次,对于每次更新的第n个路径都是通过伯努利采样得到的,然后计算适应度:
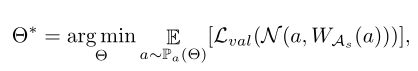
对于每一层包含K个候选操作,会计算每个操作被采样的所有组合可能的联合概率,每一个操作被选择的概率都是0.5,同时以资源作为正则项进行优化,适应度计算按照下式进行:
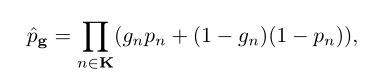
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第4张图片](http://img.e-com-net.com/image/info8/05dd388e77c54a4fa35705e6e1923db9.jpg)
延迟约束则是建立了一个查找表来记录每个操作的延迟成本获得的。
Simulated Gradients
由于计算交叉熵时无法直接得到适应度,因此也就无法通过反向传播直接更新。本文受BinaryConnect的启发将采样的分支组合输出传给下一层,其中gate是随机选择的配置,将这一梯度模拟为真正的梯度:

并且本文只选择两种配置来简化计算和对GPU内存的需求。最终梯度被近似表示为:
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第5张图片](http://img.e-com-net.com/image/info8/95aa02d4413b4c8bb47a920ba6114b87.jpg)
Pareto Front Retrieval and Architecture Aggregation
Pareto Front Retrieval
为了获得帕累托最优本文会计算采样结构的炎症精度,即随机采样D个模型,其中不满足资源约束的模型会被直接丢弃,如果最后一次搜索就包含帕累托最优结构,也被使用L&R策略进行评估。最后一轮优化后得到的P个最优结构作为最终的结果。
Aggregation
聚合就是取这P个帕累托最优结构组成的搜索空间As。
Section IV Experimental Results
Part 1 Search Space FLOPs
约束实验搜索空间包含27个不同的操作,然后在一个完整的搜索空间子集上搜索三轮获得最终的结果。
Latency约束实验包含19个候选操作。这些候选操作的数目远远超过之前一些NAS研究。
Inheritance by Search Space Replenishment
通过互补搜索空间进行继承
为了获得下一轮进化的新的搜索空间自己,会在整个搜索空间池A中随机选择一定数量的候选操作,但并不包含前面已经包含的操作作为补充操作集合Ar,同时还继承通过聚合得到的优化后的搜索空间子集As,因此新的搜索空间子集A是Ar和As的并集,这样进化后的搜索空间子集A的大小与原来的As大小相同,每层都包含K个操作。
候选操作的顺序被随机shuffle,以最小化其顺序带来的潜在影响,但每一层可能保留了不平衡的操作数目,表明某些层可能会提前选尽候选操作。本文将这种情况作为NSE搜索的终点。
其他设置:
搜索空间的层数K设置为5,延迟实验中设置为6,最终会随机选取5个帕累托最优模型并将其reshape到330M flops大小并重训练后作为输出模型。所有试验在ImageNet上进行。
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第6张图片](http://img.e-com-net.com/image/info8/a72ac74fdaa54a94b9de0f1275a8aec6.jpg)
Part 2 FLOPs约束实验
FLOPs约束实验的目标是300M FLOPs,如Table1所示,从27个ops搜索到的结果,在325M FLOPs达到了75.3%的top-1精度,已经超过了许多人工或搜索架构。当搜索空间进化一次是,最高性能达到了75.5%.如果引入其他辅助操作本文模型的性能会进一步提升。
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第7张图片](http://img.e-com-net.com/image/info8/08932a91a6d340f0b93f2814d1c738fc.jpg)
Part 3 Latency Constraint Results
本文优化的平台是Titan Xp和TensorRT框架,batch_size=16 latency目标是8ms,结果如Table 2所示,在NSE-Net-GPU获得了77.9%的top-1精度,此时延迟为8.9ms;并且指的注意的是虽然本文的搜索空间与PC-NAS-L相同但是性能提升了0.4%并且延迟缩短了1.4ms。
Part 4 Necessity of Search Space Evolution
Existing Methods on Large Search Space
第一节介绍了当前的NAS算法不适合较大的搜索空间,本文评估下面4种方法:DARTS,One-Shot,SPOS,pROXYLESS nas.
DARTS:会对所有路径进行优化,这就使得本文基于27个候选操作的搜索成本非常高,训练100epochs需要27k GPU hours;
SPOS虽然不会对所有路径进行搜索但在本文相同设置下无法较好的收敛,前100个epoch使用SPOS训练的超网并不收敛,精度为1%.搜索成本为4k GPU Hours,最终从Table 3可以看到具有300M-350M FLOPs的帕累托最优框架的精度为73.5%.
Proxyless NAS通过可学习的结构参数来逐渐缩小搜索空间,可以看到比one-shot效果要好,但是仍然比不过本文的NSE算法。
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第8张图片](http://img.e-com-net.com/image/info8/a139aff65e7d4f969e92b7831c9015de.jpg)
Search Space Simplification without Search Space Evolution
本文还探究了搜索空间简化是否可以处理较大的搜索空间,Fig 5分别展示了每层K=5和K=9的情况,他们最开始使用的是同一个搜索自己,Fig5(a)展示了第一轮搜索的结果,此时可以看到较大的初始搜索空间(K=9)会导致更差的搜索结果,也说明了如果搜索空间不进化那么较大的初始搜索空间会导致较差的结果。
Section V Ablation study
Part 1 Search Space Quality
为了验证搜索空间是否对特定任务有效,本文采用分布估计,即在搜索空间内随机抽样网络结构再训练练得到精度来评估搜索空间的质量。
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第9张图片](http://img.e-com-net.com/image/info8/19758ebe68834a3bb76c2393aa0a3300.jpg)
Fig 4(a)展示了三个搜索空间,Multi-Branch 27是本文的空间,Single-Branch-27是单分支版本的搜索空间,Single-Branch-9则是本文27OPs的一个自己,只包含核为{3,5,7}的深度卷积,可以看到单分支空间和多分支空间之间没有明显的gao,但理论上多分支的性能上限更高,而single-9的子集在重训练后有更高的架构分布,这两者之间的gap就是本文希望通过搜索空间进化解决的问题。
Part 2 Continual Convergence
为了证明本文的NSE可以持续优化搜索空间子集和搜索到的结构,本文首先随机选择了每一轮最优的5个框架,然后分别从头开始训练,从Fig 5(b)可以看到在性能方面有持续提升,而且聚合后搜索空间的质量也在逐步提高。
Part 3 Impact of Components
Layer-wise size
从Fig 4(b)可以看到 K越小最初的精度分布越差,但通过搜索空间的进化仍然可以达到较好的收敛效果,因为越小的搜索空间越容易进化。
Simplification and Aggregation
Fig 4(b)还展示了搜索空间简化-聚合的效果,可以看到二者都交大程度的提升了搜索空间的质量。
Lock and Rehearse
Fig 5(a)则展示了没有L&R这种正则化方法会带来性能的显著下降,因此L&R可以有效防止继承的搜索空间被去除。
Section VI Conclusions
本文提出一种新的神经网络搜索方案-NSE,主要对较大的搜索空间采用逐步进化精炼的方式来进化搜索空间,同时又可以保持先验知识。通过引入多分支的设置进一步扩展了架构的灵活性。可以看到NSE一方面最小化了搜索空间人工设计的参与另一方面带来了性能增益,向全自动的NAS搜索更进一步。
![[NAS]NSE:Evolving Search Space for Neural Architecture Search_第10张图片](http://img.e-com-net.com/image/info8/d42e89d5d56440fcad558e59e486f7a3.jpg)