基于混沌博弈优化算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、混沌博弈优化算法
- 2、CGO算法伪代码
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、混沌博弈优化算法
混沌博弈优化(Chaos game optimization, CGO)算法是基于混沌理论的原理提出的一种优化算法,它利用分形和混沌博弈的基本概念,建立了CGO算法的数学模型。
在该算法中,每个候选解( X i X_i Xi)由一些决策变量( x i , j x_{i,j} xi,j)组成,这些决策变量代表这些合格种子在Sierpinski三角形中的位置。在该算法中,Sierpinski三角形被视为候选解的搜索空间。数学模型如下: X = [ X 1 X 2 ⋮ X i ⋮ X n ] = [ x 1 1 x 1 2 ⋯ x 1 j ⋯ x 1 d x 2 1 x 2 2 ⋯ x 2 j ⋯ x 2 d ⋮ ⋮ ⋮ ⋱ ⋮ x i 1 x i 2 ⋯ x i j ⋯ x i d ⋮ ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n j ⋯ x n d ] , { i = 1 , 2 , ⋯ , n . j = 1 , 2 , ⋯ , d . (1) X=\begin{bmatrix}X_1\\X_2\\\vdots\\X_i\\\vdots\\X_n\end{bmatrix}=\begin{bmatrix} x_1^1 & x_1^2 & \cdots & x_1^j & \cdots & x_1^d \\x_2^1 & x_2^2 & \cdots & x_2^j & \cdots & x_2^d \\\vdots & & \vdots & \vdots & \ddots & \vdots \\x_i^1 & x_i^2 & \cdots & x_i^j & \cdots & x_i^d \\ \vdots & & \vdots & \vdots & \ddots & \vdots \\x_n^1 & x_n^2 & \cdots & x_n^j & \cdots & x_n^d \end{bmatrix},\,\,\begin{dcases}i=1,2,\cdots,n.\\j=1,2,\cdots,d.\end{dcases}\tag{1} X=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡X1X2⋮Xi⋮Xn⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡x11x21⋮xi1⋮xn1x12x22xi2xn2⋯⋯⋮⋯⋮⋯x1jx2j⋮xij⋮xnj⋯⋯⋱⋯⋱⋯x1dx2d⋮xid⋮xnd⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤,{i=1,2,⋯,n.j=1,2,⋯,d.(1)其中, n n n是Sierpinski三角形(搜索空间)内合格种子(候选解)的数量, d d d是这些种子的维数。
这些合格种子的初始位置在搜索空间中随机确定,如下所示: x i j ( 0 ) = x i , min j + r a n d ⋅ ( x i , max j − x i , min j ) , { i = 1 , 2 , ⋯ , n . j = 1 , 2 , ⋯ , d . (2) x_i^j(0)=x_{i,\min}^j+rand\cdot\left(x_{i,\max}^j-x_{i,\min}^j\right),\,\,\begin{dcases}i=1,2,\cdots,n.\\j=1,2,\cdots,d.\end{dcases}\tag{2} xij(0)=xi,minj+rand⋅(xi,maxj−xi,minj),{i=1,2,⋯,n.j=1,2,⋯,d.(2)其中, x i j ( 0 ) x_i^j(0) xij(0)表示合格种子的初始位置; x i , min j x_{i,\min}^j xi,minj和 x i , max j x_{i,\max}^j xi,maxj是第 i i i个候选解的第 j j j个决策变量的最小和最大值; r a n d rand rand是 [ 0 , 1 ] [0,1] [0,1]区间内的随机数。
该数学模型的主要概念是在搜索空间内创建不同的合格种子,以完成Sierpinski三角形的整体形状。对于搜索空间( X i X_i Xi)中的每个合格种子,将绘制一个包含3个种子的临时三角形,如下所示:
- 迄今为止全局最优解(Global Best, G B GB GB)
- 种群的平均位置(Mean Group, M G i MG_i MGi)
- 第i个候选解( X i X_i Xi)作为所选种子的位置
其中, G B GB GB指的是迄今为止发现的具有最高合格水平的最佳候选解, M G i MG_i MGi指的是一些随机选择的合格种子的平均值。
为了实现该算法的优化目标,开发了4种创建种子的方法。其中,第一个种子位于 X i X_i Xi,第二个种子位于 G B GB GB,第三个种子位于 M G i MG_i MGi,第四个种子的位置基于随机候选解产生。
第一种子产生的过程的数学表示如下: S e e d i 1 = X i + α i × ( β i × G B − γ i × M G i ) , i = 1 , 2 , ⋯ , n . (3) Seed_i^1=X_i+\alpha_i\times(\beta_i\times GB-\gamma_i\times MG_i),\,\,i=1,2,\cdots,n.\tag{3} Seedi1=Xi+αi×(βi×GB−γi×MGi),i=1,2,⋯,n.(3)其中, X i X_i Xi是第 i i i个候选解; G B GB GB是迄今为止发现的全局最优解; M G i MG_i MGi是一些选定的合格种子的平均值; α i \alpha_i αi是随机生成的阶乘,用于模拟种子的移动限制,而 β i \beta_i βi和 γ i \gamma_i γi分别表示1或2的随机整数,用于模拟掷骰子的可能性。
与第一种子的移动过程类似,第二种子可以向 X i X_i Xi和 M G i MG_i MGi之间的连接线的一点移动,并且使用一些随机生成的因子来限制该移动。该过程的数学表示如下: S e e d i 2 = G B + α i × ( β i × X i − γ i × M G i ) , i = 1 , 2 , ⋯ , n . (4) Seed_i^2=GB+\alpha_i\times\left(\beta_i\times X_i-\gamma_i\times MG_i\right),\,\,i=1,2,\cdots,n.\tag{4} Seedi2=GB+αi×(βi×Xi−γi×MGi),i=1,2,⋯,n.(4)其中, α i \alpha_i αi是随机生成的阶乘,用于模拟种子的移动限制,而 β i \beta_i βi和 γ i \gamma_i γi分别表示1或2的随机整数,用于模拟掷骰子的可能性。其他参数如第一个种子所述。
第三种子基于 M G i MG_i MGi的位置随机产生,其数学模型如下所示: S e e d i 3 = M G i + α i × ( β i × X i − γ i × G B ) , i = 1 , 2 , ⋯ , n . (5) Seed_i^3=MG_i+\alpha_i\times(\beta_i\times X_i-\gamma_i\times GB),\,\,i=1,2,\cdots,n.\tag{5} Seedi3=MGi+αi×(βi×Xi−γi×GB),i=1,2,⋯,n.(5)为了在搜索空间中合格种子的位置更新中实现变异阶段,还利用另一过程来生成第四个种子。该种子的位置更新是基于随机选择的决策变量中的一些随机变化进行的。第四种子的的数学建模如下: S e e d i 4 = X i ( x i k = x i k + R ) , k = [ 1 , 2 , ⋯ , d ] . (6) Seed_i^4=X_i(x_i^k=x_i^k+R),\,\,k=[1,2,\cdots,d].\tag{6} Seedi4=Xi(xik=xik+R),k=[1,2,⋯,d].(6)其中, k k k是 [ 1 , d ] [1,d] [1,d]区间内的随机整数, R R R是 [ 0 , 1 ] [0,1] [0,1]区间内的均匀分布随机数。
为了控制和调整CGO算法的探索和利用率,针对 α i \alpha_i αi提出了四种不同的公式,用于控制种子的移动限制: α i = { R a n d 2 × R a n d − 1 ( δ × R a n d ) + 1 ( ε × R a n d ) + ( ∼ ε ) (7) \alpha_i=\begin{dcases}Rand\\2\times Rand-1\\(\delta\times Rand)+1\\(\varepsilon\times Rand)+(\sim\varepsilon)\end{dcases}\tag{7} αi=⎩⎪⎪⎪⎨⎪⎪⎪⎧Rand2×Rand−1(δ×Rand)+1(ε×Rand)+(∼ε)(7)其中, R a n d Rand Rand是 [ 0 , 1 ] [0,1] [0,1]区间内的均匀分布随机数,而 δ \delta δ和 ε \varepsilon ε是 [ 0 , 1 ] [0,1] [0,1]区间内的随机整数。
2、CGO算法伪代码
二、仿真实验与结果分析
将CGO与GWO、WOA、SOS和TLBO进行对比,以常用23个测试函数的F1、F2(单峰函数/30维)、F10、F11(多峰函数/30维)和CEC2017测试函数的F6和F7(30维)为例,种群规模设置为50,最大迭代次数设置为500,每个算法独立运算30次。结果显示如下:

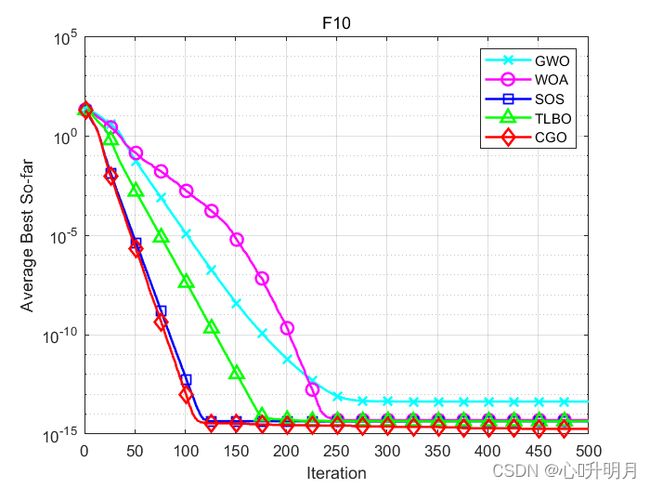
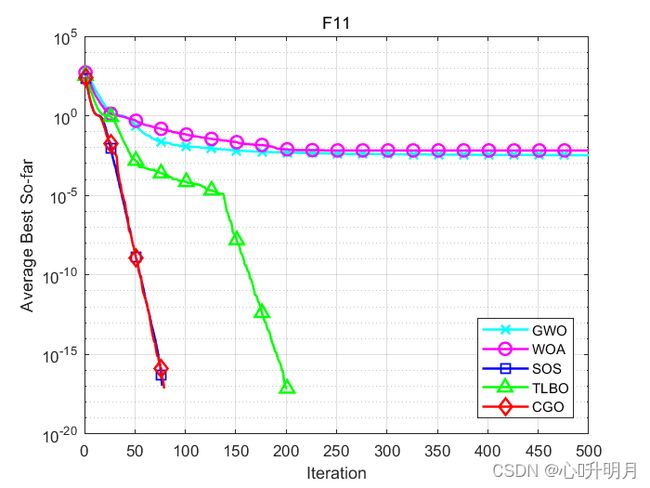
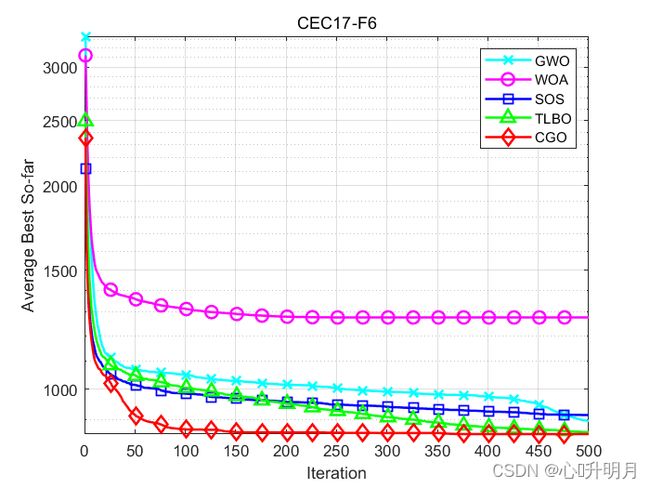
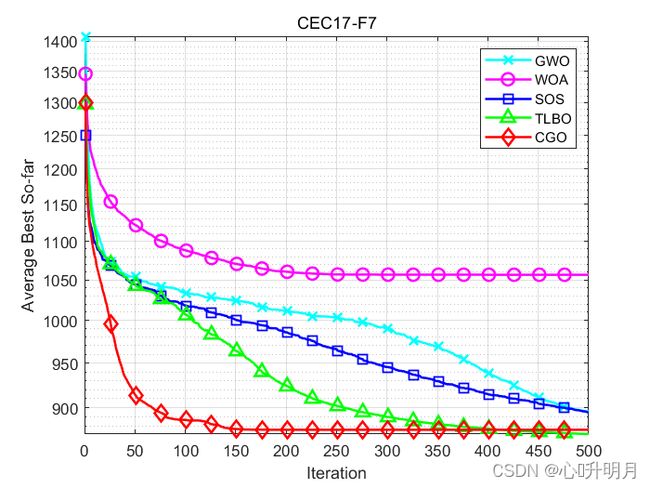
函数:F1
GWO:最差值: 9.0138e-33,最优值:5.5583e-35,平均值:1.6987e-33,标准差:1.8232e-33,秩和检验:3.0199e-11
WOA:最差值: 6.3404e-84,最优值:5.0426e-95,平均值:3.7613e-85,标准差:1.262e-84,秩和检验:3.0199e-11
SOS:最差值: 1.9813e-133,最优值:2.0348e-136,平均值:1.4282e-134,标准差:3.5494e-134,秩和检验:3.0199e-11
TLBO:最差值: 3.963e-87,最优值:1.6727e-89,平均值:1.0494e-87,标准差:1.1013e-87,秩和检验:3.0199e-11
CGO:最差值: 3.9198e-142,最优值:4.9139e-150,平均值:2.3955e-143,标准差:8.0333e-143,秩和检验:1
函数:F2
GWO:最差值: 1.859e-19,最优值:6.1822e-21,平均值:6.5773e-20,标准差:4.5807e-20,秩和检验:3.0199e-11
WOA:最差值: 5.5072e-53,最优值:1.7111e-59,平均值:2.2437e-54,标准差:1.0037e-53,秩和检验:3.0199e-11
SOS:最差值: 3.5483e-67,最优值:1.7269e-69,平均值:5.3583e-68,标准差:8.4905e-68,秩和检验:3.0199e-11
TLBO:最差值: 1.1781e-43,最优值:7.143e-45,平均值:3.5969e-44,标准差:2.394e-44,秩和检验:3.0199e-11
CGO:最差值: 5.6983e-73,最优值:0,平均值:4.4647e-74,标准差:1.1209e-73,秩和检验:1
函数:F10
GWO:最差值: 5.0626e-14,最优值:3.9968e-14,平均值:4.3165e-14,标准差:3.5343e-15,秩和检验:5.551e-12
WOA:最差值: 7.9936e-15,最优值:8.8818e-16,平均值:5.033e-15,标准差:2.8119e-15,秩和检验:1.2084e-05
SOS:最差值: 4.4409e-15,最优值:8.8818e-16,平均值:4.3225e-15,标准差:6.4863e-16,秩和检验:3.3774e-08
TLBO:最差值: 4.4409e-15,最优值:4.4409e-15,平均值:4.4409e-15,标准差:0,秩和检验:5.3591e-09
CGO:最差值: 4.4409e-15,最优值:8.8818e-16,平均值:1.8356e-15,标准差:1.5979e-15,秩和检验:1
函数:F11
GWO:最差值: 0.017041,最优值:0,平均值:0.0033471,标准差:0.0053964,秩和检验:0.0013702
WOA:最差值: 0.093766,最优值:0,平均值:0.0066683,标准差:0.021302,秩和检验:0.081523
SOS:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
TLBO:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
CGO:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
函数:CEC17-F6
GWO:最差值: 1008.7738,最优值:814.5043,平均值:897.0891,标准差:50.9036,秩和检验:0.0030339
WOA:最差值: 1448.0519,最优值:1119.6555,平均值:1276.6888,标准差:95.0696,秩和检验:3.0199e-11
SOS:最差值: 957.3604,最优值:851.0151,平均值:915.1328,标准差:27.5783,秩和检验:1.5964e-07
TLBO:最差值: 964.3504,最优值:803.85,平均值:862.9625,标准差:40.8144,秩和检验:0.48252
CGO:最差值: 975.0231,最优值:808.2228,平均值:857.5276,标准差:36.3624,秩和检验:1
函数:CEC17-F7
GWO:最差值: 1041.3225,最优值:861.6842,平均值:896.2543,标准差:35.0411,秩和检验:0.014412
WOA:最差值: 1166.4361,最优值:976.7906,平均值:1056.624,标准差:54.2451,秩和检验:3.0199e-11
SOS:最差值: 956.527,最优值:843.8169,平均值:895.1846,标准差:36.0076,秩和检验:0.059428
TLBO:最差值: 906.1988,最优值:843.0764,平均值:872.0592,标准差:16.7959,秩和检验:0.40354
CGO:最差值: 922.3795,最优值:843.7781,平均值:876.6448,标准差:21.91,秩和检验:1
所得结果证明:在大多数情况下,CGO优于其他启发式算法。
三、参考文献
[1] Talatahari, S., Azizi, M. Chaos Game Optimization: a novel metaheuristic algorithm[J]. Artificial Intelligence Review, 2021, 54: 917-1004.
