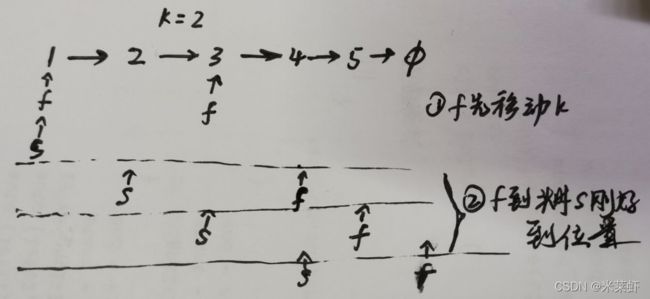高频笔试面试刷题总结之链表(分布讲解&代码注释)
JZ22 链表中倒数最后k个结点【简单】
题面
 思路
思路
- 双指针,定义两个指针:first 和 second
- 前一个指针先走 k 步,在它走的 k 步中,若发现指针 first 置空,则返回 nullptr;
- 如下图所示,接下来两指针同时向前移动,当 first 走到头置空时,second 刚好走到第 k 个位置
复杂度分析
- 时间复杂度: O(n)
- 空间复杂度: O(1)
代码
class Solution {
public:
ListNode* FindKthToTail(ListNode* pHead, int k) {
if(pHead==nullptr) return nullptr;
//定义双指针
ListNode* first = pHead;
ListNode* second = pHead;
//第一个指针先走k步
while(k > 0) {
//若链表长度小于k,返回一个长度为0的链表
if(first==nullptr) return nullptr;
first = first->next;
k--;
}
//两个指针同时前进,当前一个指针置空时,后一个指针到达
while(first!=nullptr) {
first = first->next;
second = second->next;
}
return second;
}
};JZ18 删除链表的节点【简单】
题面
思路
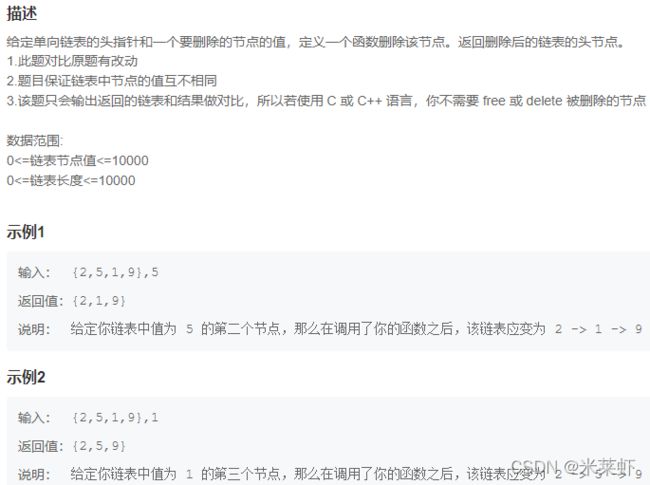
- 需要注意 链表是否为空 和 只有一个头结点不可删除 的情况
- 定义两个指针 pre 和 cur,当 cur 指向需要删除的节点时,改变 pre 的指向即可删除该节点(相当于越过了那个节点)
复杂度分析
- 时间复杂度: O(n)
- 空间复杂度: O(1)
代码
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
auto pre = head, cur = head; //cur指向要删除的那个节点,pre指向它的前驱节点
if(head->val == val) return head->next; //只有一个头结点的情况
while(cur->val != val) { //寻找需要删除的节点
pre = cur;
cur = cur->next;
}
pre->next = cur->next; //改变前驱节点pre的指向
return head;
}
};JZ76 删除链表中重复的结点【较难】
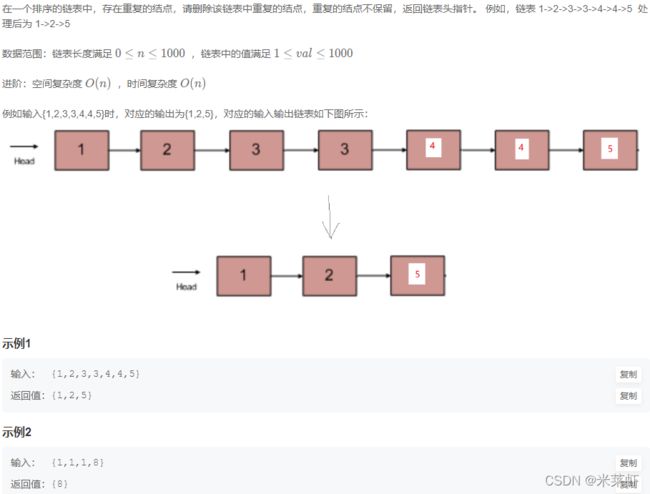
题面
思路
快慢指针
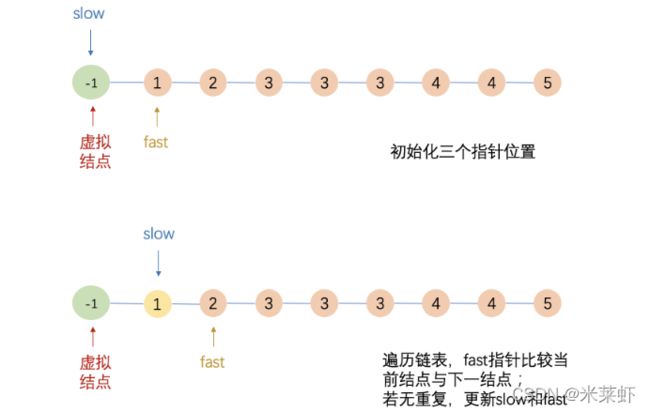
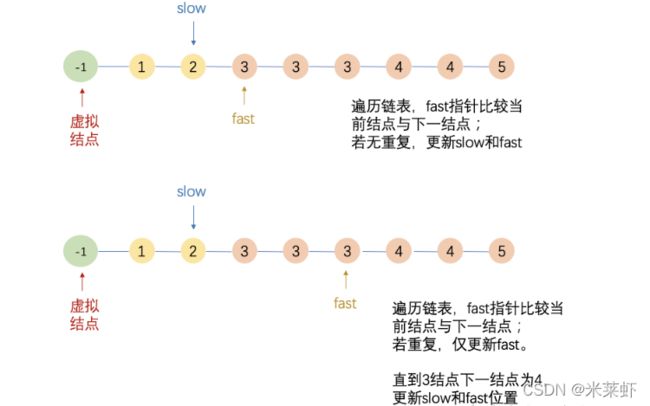
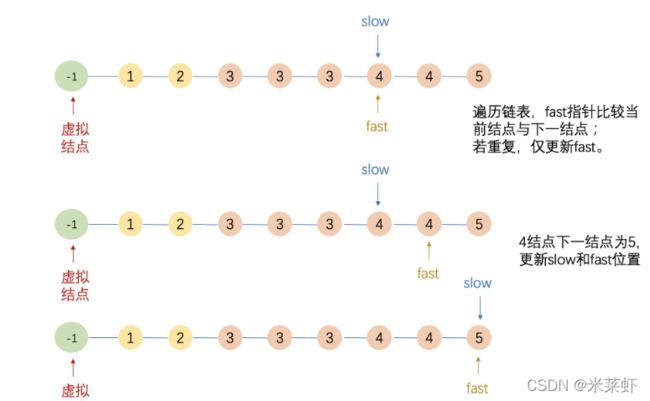
- 定义两个指针(slow、fast),以及虚拟结点dummy,初始化三者指针,slow和fast相邻;
- 当遇到重复时,「只有fast指针」向前移动,此时slow和fast不相邻;
- 若没有重复,则slow指针和fast指针都向前移动一步;
「当出现重复时,slow指针和fast指针必不相邻,此时更新二者的位置可以实现删除的效果」
具体过程如下所示:
复杂度分析
时间复杂度:O(N),该方法需要遍历整个链表
空间复杂度:O(1),除部分指针外,未使用额外空间
代码
class Solution {
public:
ListNode* deleteDuplication(ListNode* pHead) {
if(!pHead) return NULL;
ListNode* slow = new ListNode(-1), *fast = new ListNode(-1), *dummy = new ListNode(-1);
dummy->next = pHead;
// 初始化两个指针
slow = dummy; fast = dummy->next;
while(fast) {
// 遇到重复
while(fast->next && fast->val == fast->next->val) {
fast = fast->next;
}
// 遇到重复
if(slow->next != fast) {
slow->next = fast->next;
fast = slow->next;
}
// 没有重复
else {
fast = fast->next;
slow = slow->next;
}
}
return dummy->next;
}
};JZ35 复杂链表的复制【较难】
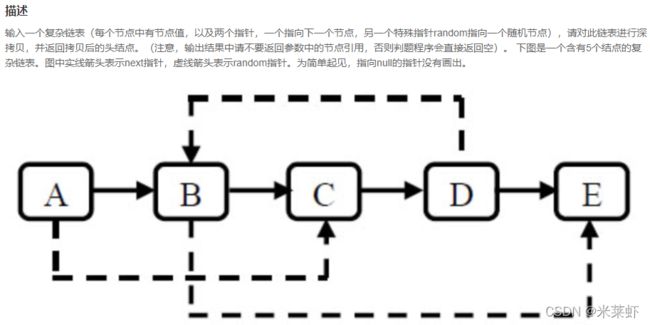
题面
代码
class Solution{
public:
RandomListNode* Clone(RandomListNode* pHead) {
if(!pHead) return nullptr;
RandomListNode* cur = pHead;
unordered_map map;
//复制各节点,并建立 “原节点 -> 新节点” 的 Map 映射
while(cur != nullptr) {
map[cur] = new RandomListNode(cur->label);
cur = cur->next;
}
cur = pHead;
//构建新链表的 next 和 random 指向
while(cur != nullptr) {
map[cur]->next = map[cur->next];
map[cur]->random = map[cur->random];
cur = cur->next;
}
//返回新链表的头节点
return map[pHead];
}
};
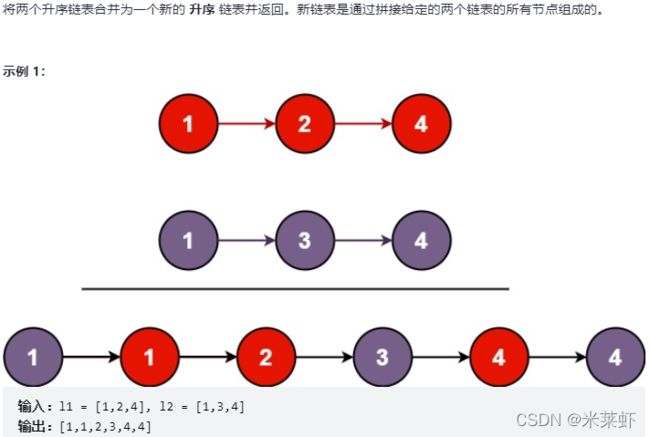
合并两个有序链表【简单】
题面
思路
- 最直接的思路就是——递归:
- 只要有一个链表为空,就直接返回另一个链表,不需要进行合并;
- 否则看两个链表哪个头部节点较小,较小的头部节点指向剩余节点的merge结果。
- 通过递归的方式将两个链表的所有节点进行合并。
复杂度分析
- 时间复杂度:O(n+m),每次调用递归都会去掉
l1或者l2的头节点(直到至少有一个链表为空),函数 mergeTwoLists 至多只会递归调用每个节点一次。 - 空间复杂度:O(n+m),递归调用 mergeTwoLists 时消耗栈空间,栈空间的大小取决于递归调用的深度。结束递归调用时,mergeTwoLists 函数最多调用 n+m 次。
代码
class Solution{
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2){
if(l1==nullptr) return l2; // l1为空链表,返回l2链表
else if(l2==nullptr) return l1; // l2为空链表,返回l1链表
else if(l1->val < l2->val) {
l1->next = mergeTwoLists(l1->next, l2); // l1头结点的值小,指向剩余节点的merge结果
return l1; // 返回合并后的l1链表
}
else {
l2->next = mergeTwoLists(l2->next, l1); // l2头结点的值小,指向剩余节点的merge结果
return l2; // 返回合并后的l2链表
}
}
};优化
- 用迭代代替递归,使得空间复杂度优化到O(1)。
- 当 l1 和 l2 都是非空链表时,判断哪个链表的头节点的值更小,将较小值的节点添加到结果里,当一个节点被添加到结果里之后,将对应链表中的节点向后移一位。
- 首先,设定一个哨兵节点 prehead ,使返回合并后的链表更简单。维护一个 prev 指针,重点在于调整它的 next 指针。如果 l1 当前节点的值小于等于 l2 ,我们就把 l1 当前的节点接在 prev 节点的后面同时将 l1 指针往后移一位。否则,我们对 l2 做同样的操作。不管我们将哪一个元素接在了后面,我们都需要把 prev 向后移一位。直到 l1 或者 l2 指向了 null。
- 循环终止时, l1 和 l2 至多有一个非空。由于两个链表都有序,所以不管哪个链表是非空的,它包含的所有元素都比前面已经合并链表中的所有元素都要大。只需要简单地将非空链表接在合并链表的后面,并返回合并链表即可。
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* preHead = new ListNode(-1);
ListNode* prev = preHead;
while (l1 != nullptr && l2 != nullptr) {
if (l1->val < l2->val) {
prev->next = l1;
l1 = l1->next;
}
else {
prev->next = l2;
l2 = l2->next;
}
prev = prev->next;
}
// 合并后,最多只有一个链表还未被合并完,直接将链表末尾指向未合并完的链表
prev->next = l1 == nullptr ? l2 : l1;
return preHead->next;
}
};相交链表 & JZ52 两个链表的第一个公共结点【简单】
题面
思路
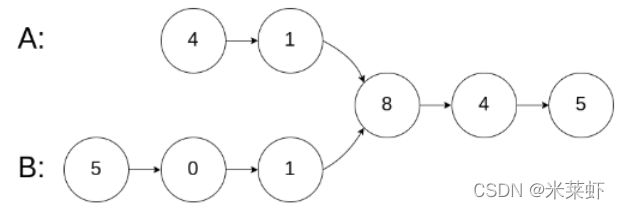
基础的想法是哈希集合存储链表节点:先遍历链表 A,并将每个节点加入哈希集合中;然后遍历 B,遍历到的每个节点,判断该节点是否在哈希集合中。直到找到 B 中在 A 中的节点,并且从这个节点开始,所有的节点都重合,那这个点就是要找的。
双指针将空间复杂度降至O(1)
具体做法如下:
给出一个例子,制造一种理想的情况:当两个链表长度相等的时候,就可以用双指针来解决了
- 初始化:指针ta指向链表A的头结点,指针tb指向链表B的头结点
- 若 ta==tb,则说明到达了第一个公共节点;
- 否则(ta != tb),两指针一起后移一个单位(ta++;tb++)
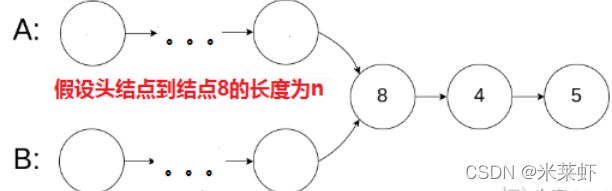
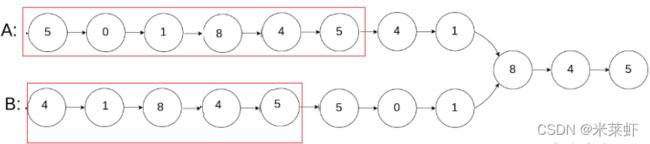
那么,如何让两个链表长度相等呢?
假设链表A长度为a,链表B长度为b,显然a!=b,但是a+b==b+a
因此,可以让a+b作为A新的长度,让b+a作为B新的长度
此时,长度一样,可以使用双指针算法
两大类 “双指针” 算法剖析【附例题详解+AC代码】_夏旭的博客-CSDN博客首先,介绍一下双指针算法。我们在用朴素算法暴力解决问题时,通过挖掘某些性质,使得算法复杂度由 O(n^2)->O(n) ,我们把具有这样性质的算法称为双指针算法【其实双指针算法非常广泛,不只是被用在维护两个窗口上,但在这里,我们缩小了它的范围】。常用的两种双指针算法的类型:一种是: 两个指针分别指向两个序列 ( “归并排序” 就用到了这一种指针,具体操作:每一次分别移动两个指针,两个指针移动完的时候,排序过程即结束);另一种是: 两个指针指向同一个序列,一个指向开头,一个指向结尾 (如快排)。https://blog.csdn.net/Luoxiaobaia/article/details/106182893
复杂度分析
- 时间复杂度:哈希和双指针算法都是O(n+m),最坏情况下,公共结点为最后一个,需要遍历m+n个结点
- 空间复杂度:哈希的是O(m),哈希集合存储链表 A 中的全部节点;双指针算法则将空间复杂度优化到了O(1)。
代码
// 双指针算法
class Solution {
public:
ListNode* FindFirstCommonNode(ListNode* pHead1, ListNode* pHead2) {
ListNode* ta=pHead1, *tb=pHead2; //定义两个指针分别指向两个链表的头结点
while(ta!=tb) { //当两个指针不处于同一位置,即未到达公共节点时
//未到达公共节点时,不断指向链表1的下个节点,到尾再指向2的(保证长度相等)
ta = ta ? ta->next : pHead2;
//未到达公共节点时,不断指向链表2的下个节点,到尾再指向1的(保证长度相等)
tb = tb ? tb->next : pHead1;
}
return ta; //按要求返回第一个公共结点
}
};环形链表【简单】
题面
思路
最简单的思路就是:遍历所有的节点,判断该节点是否被此前是否被访问过。具体使用哈希表存储访问完的节点,若到达的节点已经存在于哈希表中,就说明该链表是环形的,否则加入该节点,直到遍历完整个链表。
复杂度分析
- 时间复杂度:O(N),N 表示链表中的节点数。最坏情况下要遍历每个节点一次。
- 空间复杂度:O(N),N 表示链表中的节点数。主要为哈希表的开销,最坏情况下要将每个节点插入到哈希表中一次。
代码
// 哈希表
class Solution{
public:
bool hasCycle(ListNode *head) {
unordered_set seen; // 建立哈希表
while(head != nullptr) { // 未遍历完链表时
if(seen.count(head)) return true; // 若某节点重复出现,说明是环形链表,返回true
seen.insert(head); // 若仅第一次出现,存入哈希表
head = head->next; // 指向下一个节点
}
return false; // 不是环形返回false
}
}; 进阶算法_快慢指针
要用O(1)内存解决,就要用到快慢指针。
说道快慢指针,我们就需要对 Floyd判圈(龟兔赛跑)算法 有所了解。
假设有一只兔子和乌龟在同一条链表上移动且兔子比乌龟跑得快,若没有环,则兔子会一直在乌龟前面;若有环,则兔子会优先进入环,然后一直在环内循环跑,这样乌龟也总会进入到环然后循环,也就有了相遇的可能。
定义两个指针(一快一慢)来模拟兔子和乌龟,慢指针一次移动一步,快指针一次移动两步。我们将快指针设置在慢指针前面一个位置(慢指针在head位置,快指针在head.next位置),这样能更好地说明慢指针能否追上快指针的情景(若快指针到链表尾部都没有被追上的话,就说明没有环);也能保证下方代码的while能够循环起来(如果是do-while语句的话,快慢指针的初始位置可以一样)。
快慢指针代码
// 快慢指针
class Solution {
public:
bool hasCycle(ListNode* head) {
if(head==nullptr || head->next==nullptr)
return false;
ListNode* slow = head;
ListNode* fast = head->next;
while(slow != fast) {
if(fast==nullptr || fast->next==nullptr)
return false;
slow = slow->next;
fast = fast->next->next;
}
return true;
}
};
优化后复杂度分析
- 时间复杂度:O(N),其中 N 是链表中的节点数。当链表中不存在环时,快指针将先于慢指针到达链表尾部,链表中每个节点至多被访问两次;当链表中存在环时,每一轮移动后,快慢指针的距离将减小一。而初始距离为环的长度,因此至多移动 N 轮。
- 空间复杂度:O(1),只使用了两个指针的额外空间。
反转链表【简单】
题面
思路
- 借助双指针不断实现局部反转
- 先定义两个指针,pre->head,cur->null,pre在cur前面。
- 当pre->next=cur时,就完成了当前两个指针对应位置的节点的指向的局部反转。
- 然后两个指针不断向前移动直到遍历完整个链表即可。
- 下图是 两个指针移动的部分过程 和 局部反转的示意图
复杂度分析
- 时间复杂度:O(N)
- 空间复杂度:O(1),使用了两个指针的额外空间
代码
class Solution{
public:
ListNode* reverseList(ListNode* head) {
ListNode* cur = nullptr, *pre = head;
while(pre != nullptr) {
ListNode* temp = pre->next; //记录下个节点的位置
pre->next = cur; //局部反转
cur = pre; //cur往前移动一个单位
pre = temp; //pre往前移动一个单位
}
return cur; //返回反转后的链表
}
};两数相加【简单】
题面及2种思路详解
哈希算法介绍及使用【力扣-HOT-100之“两数之和”】_夏旭的博客-CSDN博客1. 两数之和【难度】简单目录题面:题解:思路1:代码1:思路2:代码2:哈希算法的一些介绍:图解说明哈希表的用法:题面:给定一个整数数组nums和一个整数目标值target,请你在该数组中找出和为目标值target 的那两个整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。示例 1:输入:nums = [2,7,11,15], target ...https://blog.csdn.net/Luoxiaobaia/article/details/121214481
代码1&2
class Solution {
public:
vector twoSum(vector& nums, int target) {
int n = nums.size();
for (int i=0; i class Solution {
public:
vector twoSum(vector& nums, int target) {
unordered_map hashtable;
for (int i=0; isecond, i};
}
hashtable[nums[i]] = i;
}
return {};
}
}; 环形链表2【中等】& JZ23 链表中环的入口结点
题面
思路
最简单的思路就是:遍历所有的节点,判断该节点是否被此前是否被访问过。具体使用哈希表存储访问完的节点,若到达的节点已经存在于哈希表中,就说明该链表是环形的,否则加入该节点,直到遍历完整个链表。
复杂度分析
- 时间复杂度:O(N),N 表示链表中的节点数。最坏情况下要遍历每个节点一次。
- 空间复杂度:O(N),N 表示链表中的节点数。主要为哈希表的开销,最坏情况下要将每个节点插入到哈希表中一次。
代码
class Solution {
public:
ListNode *detectCycle(ListNode *head)
{
unordered_set visited;
while (head != nullptr) {
if (visited.count(head)) return head;
visited.insert(head);
head = head->next;
}
return nullptr;
}
};
进阶_快慢指针
空间复杂度优化到O(1)
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
while (fast != nullptr) {
slow = slow->next;
if (fast->next == nullptr)
return nullptr;
fast = fast->next->next;
if (fast == slow) {
ListNode *ptr = head;
while (ptr != slow) {
ptr = ptr->next;
slow = slow->next;
}
return ptr;
}
}
return nullptr;
}
};重排链表【中等】
题面
思路
- 将链表分为前半部分和后半部分。用快慢指针找到中点(分割点),即位于n/2的点。可以用快慢指针找到这个点。同时这个点也是重排后链表的最后一个点,所以将它的next指针置空。
- 从中点开始翻转后半段链表。
- 将后半段链表按间隔一个节点的规则插入到前半段链表中。
复杂度分析
- 时间复杂度:O(N)
- 空间复杂度:O(1),使用了两个指针的额外空间
代码
class Solution {
public:
void reorderList(ListNode* head) {
// 链表如果只有三个节点则无需重排(重排后结果无差别)
if(!head || !head->next || !head->next->next) return;
// 利用快慢指针找出中点s
auto s=head, f=head; //定义快慢指针
while(f && f->next) { //一直到快指针走到尾
s = s->next; //慢指针每次移动一个单位
f = f->next->next; //快指针每次移动两个单位
}
auto pre = s, cur = s->next; //提前记录下中点和下一个节点(后半部分的头结点)
s->next = nullptr; //将中点s(即重排后链表的最后一个节点)的next置空
// 反转后半部分链表,结合 “双指针实现反转链表” 理解
while(cur) {
auto o = cur->next;
cur->next = pre;
pre = cur;
cur = o;
}
//按规则将前后半段链表组合起来(合并链表)
auto p = head, q = pre;
while (q->next) {
auto o = q->next;
q->next = p->next;
p->next = q;
p = q->next;
q = o;
}
}
};二叉搜索树与双向链表【中等】
题面
思路
< 本题借鉴 林深时见鹿L6
首先介绍一下二叉搜索树:
二叉搜索树是一棵有序的二叉树,所以我们也可以称它为二叉排序树。
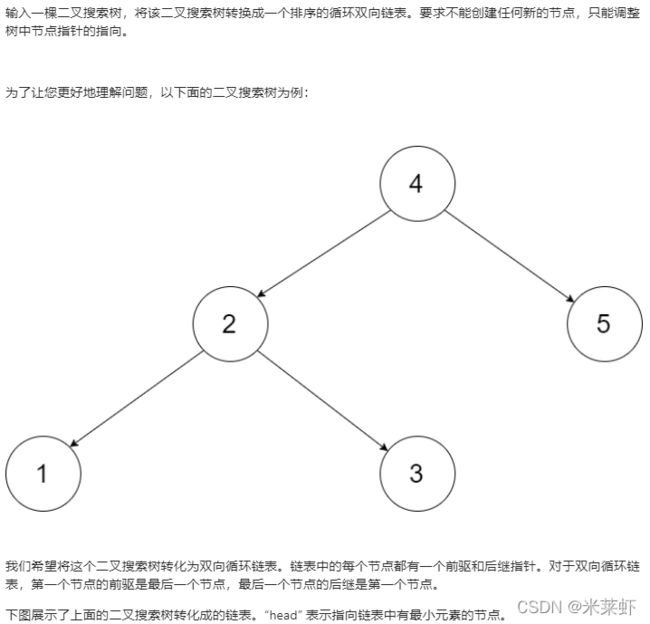
具有以下性质的二叉树我们称之为二叉搜索树:若它的左子树不为空,那么左子树上的所有值均小于它的根节点;若它的右子树不为空,那么右子树上所有值均大于它的根节点。它的左子树和右子树分别也为二叉搜索树。
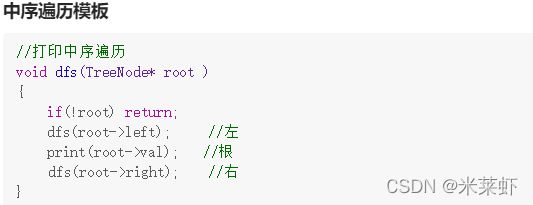
二叉搜索树的中序遍历是:左=>根=>右; 二叉搜索树的中序遍历从小到大是有序的。
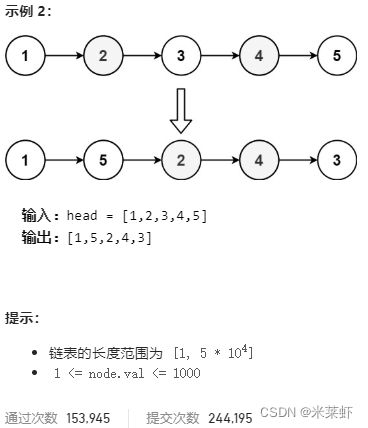
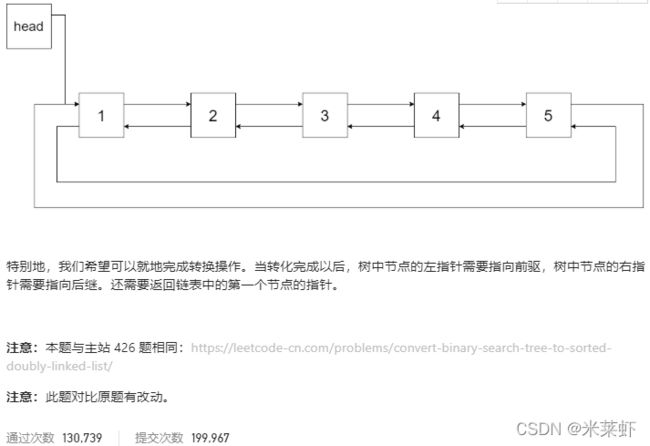
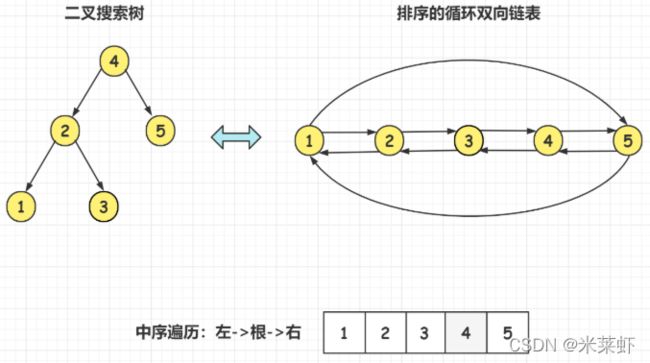
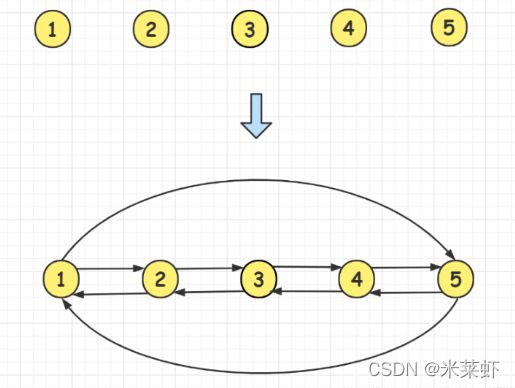
如下图所示,本题要求我们要将一棵二叉搜索树变成排序的循环双向链表
二叉搜索树的中序遍历就是有序的,因此这道题就是在中序递归遍历的基础上改了一点。
具体过程如下:
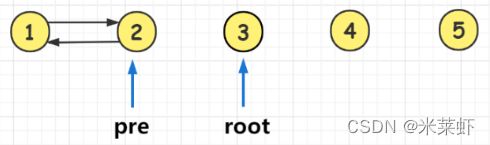
1、我们定义两个指针pre和head,pre指针用于保存中序遍历的前一个节点,head指针用于记录排序链表的头节点。
2、中序遍历二叉树,因为是中序遍历,所以遍历顺序就是双线链表的建立顺序。我们只需要在中序遍历的过程中,修改每个节点的左右指针,将零散的节点连接成双向循环链表。
3、首先遍历二叉树的左子树,然后是当前根节点root。
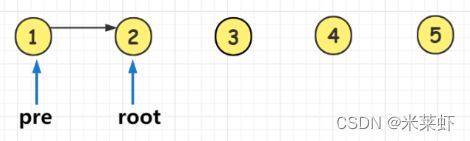
- 当前驱节点pre不为空时,将前驱节点pre的右指针指向当前根节点root,即pre->right = root。
- 当前驱节点
pre为空时: 代表正在访问链表头节点,记为head = root,保存头节点。
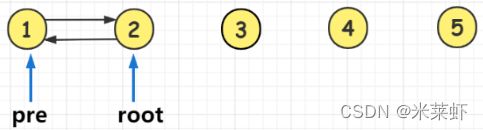
4、每一个root节点访问时它的左子树肯定被访问过了,因此放心修改它的left指针,将root的left指针指向它的前驱节点,即 root->left = pre, 这样两个节点之间的双向指针就修改好了。
5、然后前驱节点pre右移到当前root节点,接下来递归到右子树重复上述操作。
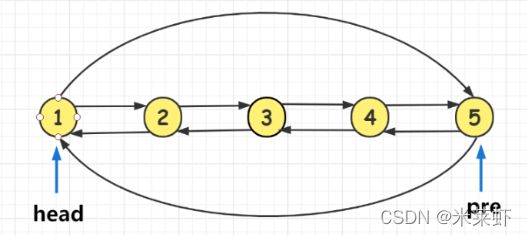
6、完成以上各步,只是将二叉树变成了双向排序链表,我们还需要将链表的首尾连接到一起,将其变成双向循环排序链表。
执行以下操作:
head->left = pre;
pre->right = head;
复杂度
n为二叉树的节点数, 中序遍历需要访问所有节点,因此时间复杂度为O(n)
代码
class Solution {
public:
Node* pre = nullptr, *head = nullptr;
Node* treeToDoublyList(Node* root) {
if (!root) return root;
dfs(root);
head->left = pre;
pre->right = head;
return head;
}
void dfs(Node* root){
if (!root) return;// 递归边界: 叶子结点返回
dfs(root->left); //左子树
if (pre) pre->right = root;
else head = root; // 保存链表头结点
root->left = pre;
pre = root;
dfs(root->right); //右子树
}
};