简介
概念
堆是一种比较特殊的数据结构,它用数组实现的二叉树,并且总是满足以下性质:
- 堆总是一棵完全二叉树
- 堆中某个结点总是不大于或不小于其父结点的的值
属性
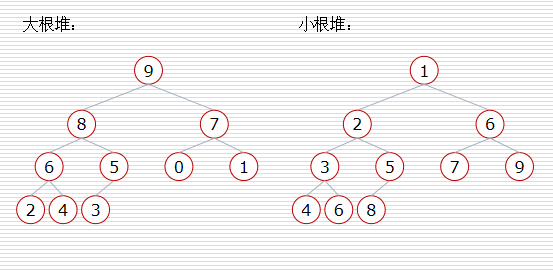
堆分为两种:根结点最大的堆叫作最大堆或大根堆;根结点最小的堆叫作最小堆或小根堆。
堆属性非常有用,其使得堆常常被当做优先队列使用,因为可以快速地访问到“最重要”的元素。
堆和二叉搜索树的区别
堆并不能取代二叉搜索树,它们之间有相似之处也有一些不同。两者的主要区别如下:
| 属性 | 堆 | 二叉搜索树 |
|---|---|---|
| 结点的顺序 | 在最小堆中父结点必须比子结点小,在最大堆中父结点必须比子结点大,变化是从上到下 |
左子结点比父结点小,父结点比右子结点小,变化是从左到右 |
| 内存占用 | 使用数组作为底层存储结构,占用内存空间较小 | 使用链表作为底层存储结构,占用内存空间较大 |
| 平衡 | 不需要整棵树有序 | 必须是平衡的,总体上是有序的 |
| 搜索 | 搜索很慢 | 搜索很快 |
堆的实现
存储
实现一个堆,首先是涉及到如何存储一个堆。
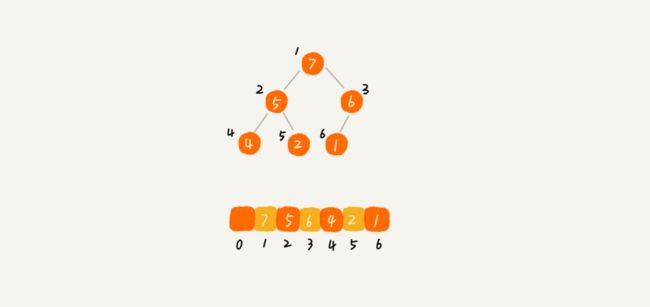
根据堆总是一棵完全二叉树的性质,以及完全二叉树比较适合用数组来存储的概念,可以知道用数组存储堆是比较好的选择。
从上图可以看到,数组中下标为 i 的结点的左子结点,就是下标为 2i 的结点,右子结点就是下标为 2i + 1 的结点,父结点就是下标为 i/2 的结点。
堆化
往堆中插入或者删除一个元素后,重要的是需要继续满足堆的两个特性,而这个重新满足堆特性的过程称为堆化。
堆化实际上有两种:从下往上、从上往下。
插入元素
插入元素时涉及的是从下往上的堆化方法。
往堆中插入一个元素其实就是往底层数组的末尾添加元素,下面是示例图:
从下往上堆化的过程比较简单,实际上就是将插入的元素与父结点进行比较,出现不符合特性的情况就互换两个结点,一直重复这个过程,直至父子结点之间满足堆的特性。
删除元素
从堆的特性可以看出,堆顶元素存储的就是堆中数据的最大值或最小值。
当删除堆顶元素的时候,为保持堆的特性,则会涉及到从上往下的堆化方法。
从上往下堆化不是直接从堆顶元素开始与子结点进行互换,而是先将数组中的最后一个元素移到被删除结点位置(为了满足完全二叉树的特性),然后利用同样的父子结点比对方法。
通常,对于大根堆会比较较大的子结点,对于小根堆会比较较小的子结点,出现不符合特性的情况就互换两个结点,一直重复这个过程,直至父子结点之间满足堆的特性。
这种方法堆化之后的结果,肯定满足完全二叉树的特性。
复杂度
一个包含 n 个节点的完全二叉树,树的高度不会超过 \(\log_2n\)。
堆化的过程是顺着节点所在路径比较交换的,所以堆化的时间复杂度跟树的高度成正比,也就是 \(O(\log n)\)。
插入数据和删除堆顶元素的主要逻辑就是堆化,所以往堆中插入一个元素和删除堆顶元素的时间复杂度都是 \(O(\log n)\)。