Python 随机（random）模块的不可预测之美

1 . 概念

1.1 真、伪随机数

大部分的计算机语言都会提供 API 生成随机数，此类 API 称为随机数生成器。

计算机可以用随机数模拟现实世界中的各种随机概率问题，没有随机生成器的编程语言不是“好语言”。

什么是真随机数？

现实世界中的随机数：比如掷钱币、骰子、转轮、使用电子元件的噪音、核裂变等等。

计算机通过硬件技术摸拟现实世界中这种物理现象所生成的随机数，我们称其为真随机数。这样的随机数生成器叫做物理性随机数生成器。生成真随机数对计算机的硬件技术要求较高。

真正随机数的特点：不可预测。

如在掷硬币时，你无法真正预测到下一次硬币的面向。

什么是伪随机数？

由算法摸拟生成的随机数称其为伪随机数。计算机编程语言中所生成的随机数基本上都是伪随机数。

伪随机数的特点：既然是由算法模拟的，虽然在一个较短的周期内是无法预测的，在一个较长的周期内的随机数具有可预测性。

1.2 随机数种子

生成伪随机数时，需要设置随机种子，种子作用就是在随机数的生成算法里注入一个动态变化量。

比如说使用系统的当前时间做随机种子，随机算法就可以在时间变化的基础上生成随机性更大的随机数。但是，如果不是在毫秒级别下生成随机数，同一时间点下所生成的大量随机数就有可能出现相等的情况。

选择种子时，可以考虑综合多维度的变化值进行运算。如在 UNIX 系统中，将系统时间、连入WIFI、甚至按下的键盘次数都量化为了seed。

参考指标越多，伪随机数就越接近真正的随机生成。

2. Python random 模块

random 模块实现了各种分布的伪随机数生成器。因为完全确定性，它不适用于所有目的，并且完全不适合加密目的。不应将此模块的伪随机生成器用于安全目的。有关安全性或加密用途，可使用 Python 中的 secrets 模块。

使得之前需要导入 random 模块

import random

2.1 随机模块的方法

初始化随机种子

random.seed(a=None, version=2)

如果 a 被省略或为 None ，则使用当前系统时间做随机种子。
如果操作系统提供随机源，则使用它们而不是系统时间。

如果 a 是 int 类型，则直接使用。

当设置随机种子是一个常量，则每一次随机数是固定的。

import random
#设置随机种子是一个 int 常量
random.seed(10)
print(random.random())
#设置随机种子是一个 int 常量
random.seed(10)
print(random.random())
#设置随机种子是一个 int 常量
random.seed(10)
print(random.random())

输出结果：

0.5714025946899135
0.5714025946899135
0.5714025946899135

从一个数字范围内产生随机数字

 random.randrange(start, stop[, step])

从 range(start, stop, step) 返回一个随机选择的元素。

这相当于 choice(range(start, stop, step))，但实际上并没有构建一个 range 对象。

返回随机整数

   random.randint(a, b)

相当于 randrange(a, b+1)

结果 N 满足： a <= N <= b

从非空序列 seq 返回一个随机元素。如果 seq 为空，则引发 IndexError 异常。

random.choice(seq)

import random

lst = [5, 3, 90, 12, 4, 6]
r = random.choice(lst)
print(r)

每一次运行会从列表中随机获得一个数字。

将序列 x 随机打乱

andom.shuffle(x[, random])

可选参数 random 是一个无参数函数，在 [0.0, 1.0) 中返回随机浮点数；默认情况下，这是函数 random()

import random

lst = [5.0, 3.0, 90.0, 12.0, 4.0, 6.0]
#使用 random.random 函数
random.shuffle(lst, random.random)
print(lst)
#输出结果
[3.0, 90.0, 6.0, 12.0, 5.0, 4.0]
#----------------------------------
def my_random():
    return float(random.randint(0, 1))

lst = [5.0, 3.0, 90.0, 12.0, 4.0, 6.0]
#使用用户自定义函数
random.shuffle(lst, my_random)
print(lst)

返回从总体序列或集合中选择的唯一元素的 k 长度列表。用于无重复的随机抽样。

random.sample(population, k, *, counts=None)

返回 [0.0, 1.0) 范围内的下一个随机浮点数。

random.random()

返回一个随机浮点数 N

random.uniform(a, b)

取决于等式 a + (b-a) * random() 中的浮点舍入，终点 b 可以包括或不包括在该范围内。

结果 N 满足：当 a <= b 时 a <= N <= b ，当 b < a 时 b <= N <= a 。

更多方法可查阅官方文档。

3. 不可预测之美

3.1 随机彩色点

解题思路： 可结合 turtle 模块绘制，随机小海龟出现的位置就可以了

import random
import turtle

colors = ["red", "blue", "green", "gray", "orange"]
for i in range(100):
    turtle.penup()
    x = random.randint(-300, 300)
    y = random.randint(-300, 300)

    turtle.goto(x, y)
    turtle.pendown()
    turtle.dot(20, colors[i % 5])

turtle.done()

3.2 求 π 的值

概率法又称为蒙特卡罗法，是一种非常重要的数值计算方法。

该方法是以概率和统计理论方法为基础的一种计算方法。将所求解的问题同一定的概率模型相联系，用计算机实现统计模拟或抽样，以获得问题的近似解。

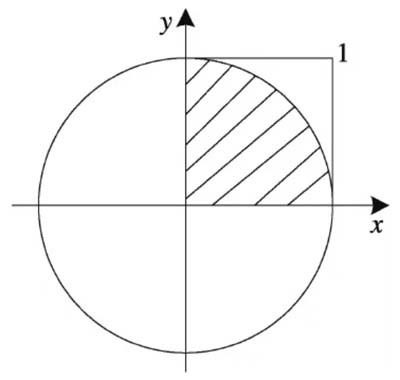
假设有一个半径为 1 的圆，如图所示，则图中阴影部分（1/4圆）的面积就等于值的1/4。通过概率法计算出阴影部分的面积，也就得到了π 值的 1/4，将阴影部分面积乘以 4 即可得到 π 的近似值。

求解思路

利用随机函数产生横坐标的值 x 和纵坐标的值 y（这两个值都应在0~1）
判断由这两个随机数构成的点是否位于1/4圆的区域内（阴影部分），若该点位于阴影区域内则进行计数。
不断产生新的点，由于随机函数生成的点坐标有一定的均匀性，当生成的点足够多时，就可得到阴影内和阴影外点的近似均匀分布。
最后用在阴影内的点的数量除以总的点数，即可得到近似的阴影面积，也就得到了一个的1/4的近似值。

  import random
  
  i, n, s = 0, 0, 0
  x, y = 0.0, 0.0
  n = int(input("输入点的数量："))
  random.seed()
  for i in range(n):
      x = random.random()
      y = random.random()
      if (x * x + y * y) <= 1:
          s += 1
  
print("PI=%f\n", 4 * s / n)

输出结果：

输入点的数量：9000000
PI= 3.141477777777778

输入的点数量越多，得到的 PI 的近似值就会越精确。

4 . 总结

随机数可以完美地模拟真实世界里的各种概率或随机事件。python 的随机数生成除了可以使用 random 模块外，还可以使用 numpy 库中所提供的方法。