【JavaSE与数据结构】数据结构之二叉搜索树

⭐️前面的话⭐️

本篇文章带大家认识数据结构——二叉搜索树，本文将介绍搜索树的概念以及使用java实现二叉搜索树。

博客主页：未见花闻的博客主页
欢迎关注点赞收藏⭐️留言
本文由未见花闻原创，CSDN首发！
首发时间：2022年3月10日
✉️坚持和努力一定能换来诗与远方！
参考书籍：《Java核心技术》，《Java编程思想》，《Effective Java》
参考在线编程网站：牛客网力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

---

---

---

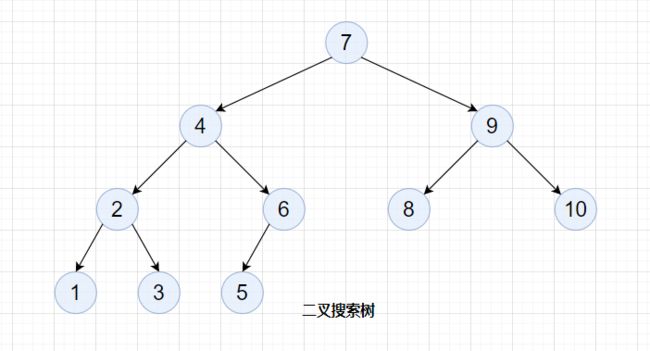
1.搜索树的概念

二叉搜索树是一种特殊的二叉树，又称二叉查找树，二叉排序树，它有几个特点：

• 如果左子树存在，则左子树每个结点的值均小于根结点的值。
• 如果右子树存在，则右子树每个结点的值均大于根结点的值。
• 中序遍历二叉搜索树，得到的序列是依次递增的。
• 二叉搜索树的左右子树均为二叉搜索树。
• 二叉搜索树的结点的值不能发生重复。

2.二叉搜索树的简单实现

我们来简单实现以下搜索树，就不使用泛型了，二叉搜索树基本结构：

public class BinarySearchTree {

    static class Node {
        public int val;
        public Node left;
        public Node right;
        public Node(int val) {
            this.val = val;
        }
    }

    public Node root;
    //其他方法
}

2.1查找

二叉搜索树最擅长的就是查找，根据二叉搜索树的定义，左子树的元素比根小，右子树的元素比根大，所以我们只需要根据根结点的值与目标元素的值比较，就能实现查找功能。

• 根与目标元素相等，表示找到了。
• 根比目标元素大，去左子树找。
• 根比目标元素小，去右子树找。
• 左右子树找不到，那就找不到了。

参考实现代码：

    public Node search(int key) {
        Node cur = this.root;
        while (cur != null) {
            //根与目标元素相等，表示找到了。
            if (cur.val == key) return cur;
            //根比目标元素大，去左子树找。
            else if (cur.val > key) cur = cur.left;
            //根比目标元素小，去右子树找。
            else cur = cur.right;
        }
        //此时cur = null, 左右子树找不到，那就找不到了。
        return cur;
    }

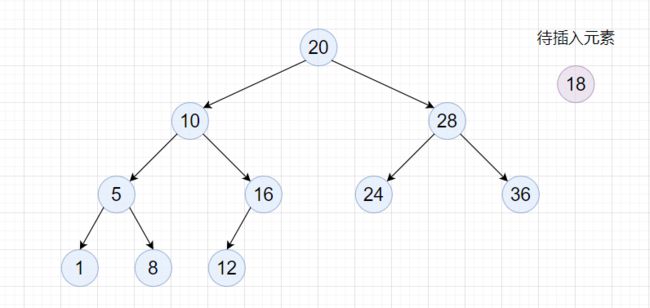
2.2插入

需要在二叉搜索树中插入一个元素，首先得找到一个合适的插入位置，如何找呢？其实就是利用搜索树查找的方式，找到一个空位，如何将目标结点插入到这个位置。

• 根与插入元素相等，插入元素不能与搜索树中的元素相等，插入失败。
• 根比插入元素大，去左子树找。
• 根比插入元素小，去右子树找。
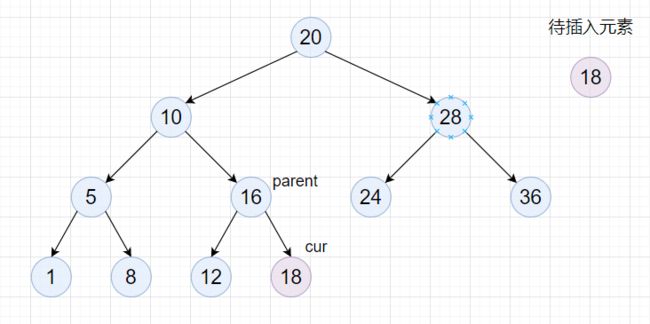
• 找到的结点为空，那这个位置就是我们要找的空位。

由于你找到空位时，无法获取该空位的前一个位置，所以每次查找的时候都需要保存上一次查找的位置。

找到位置后，将目标结点插入到该位置。

参考实现代码：

    public boolean insert(int val) {
        //结点为空，直接插
        if(root == null) {
            root = new Node(val);
            return true;
        }
        Node cur = this.root;   //当前查找位置
        Node parent = null;     //查找的上一个位置
        while (cur != null) {
            parent = cur;
            if (val > cur.val) cur = cur.right;
            else if (val < cur.val) cur = cur.left;
            else return false;
        }
        //开始插入，找到空位前一个位置，比插入元素小，空位在右边，插入右边
        if (val > parent.val) {
            parent.right = new Node(val);
        } else {
            //比插入元素大，空位在左边，插入左边
            parent.left = new Node(val);
        }
        return true;
    }

2.3删除

删除是搜索树基本操作中最麻烦的一个操作，需要考虑多种情况。
不妨设需要删除的结点为cur，cur的父结点为parent，搜索树的根结点为root。首先需要删除结点，那就得找到结点，所以第一步是找结点，思路与查找的思路一模一样。

第二步那就是删除了，删除结点大概有下面几种情况：

情况1：cur.left == null

• cur == root，让root = cur.right;
• cur != root且parent.left == cur，让parent.left = cur.right;
• cur != root且parent.right == cur，让parent.right = cur.right。

情况2：cur.right == null

• cur == null，让root = cur.left;
• cur != root且parent.left == cur，让parent.left = cur.left;
• cur != root且parent.right == cur，让parent.right = cur.left。

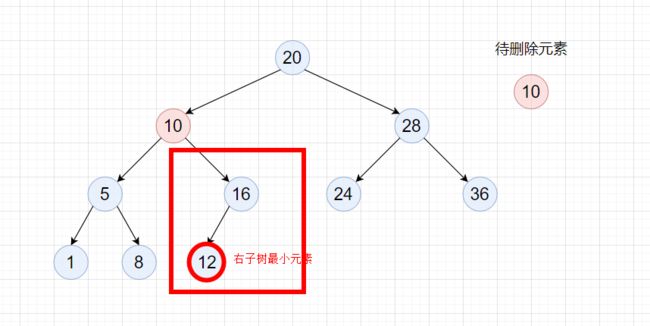
情况3：cur.left != null && cur.right != null

方案1：找到cur右子树中最小的元素target，然后将该元素的值覆盖到cur处（可以理解为交换），此时等价于删除target处的结点，即该结点的父结点为preTarget。

因为target为cur右子树最小的一个结点，所以target.left == null，此时preTarget.left == target，所以删除时按照上面的情况1去进行删除。

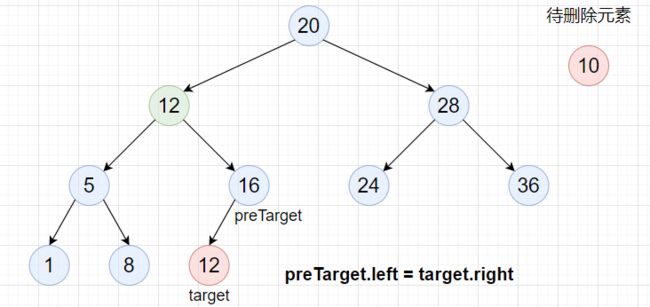
但是还有一种特殊情况，那就是cur.right就是最小结点，此时preTarget==cur，即preTarget.right == target，这时删除时要将 preTarget.right = target.right。

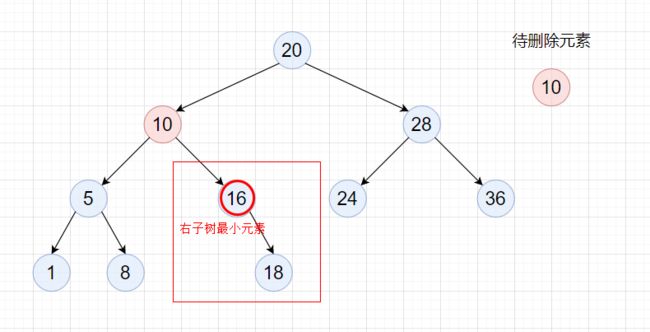
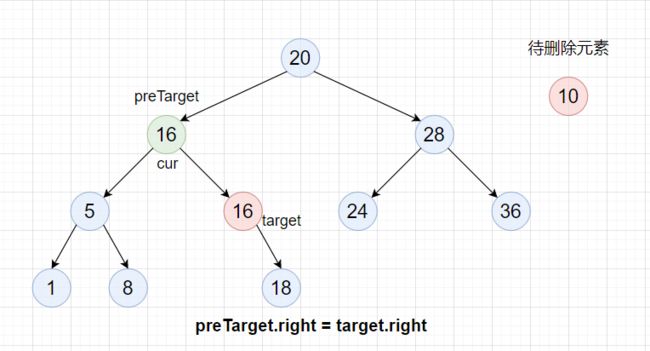
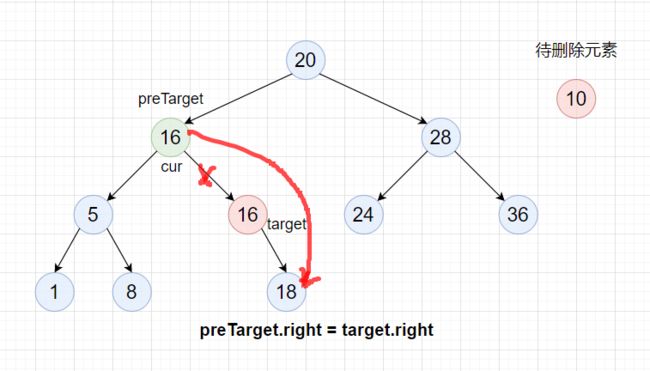
方案2：找到cur左子树中最大的元素target，然后将该元素的值覆盖到cur处（可以理解为交换），此时等价于删除target处的结点，即该结点的父结点为preTarget。

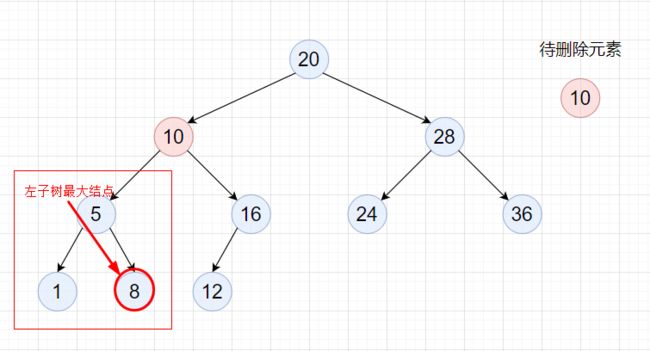
因为target为cur左子树最大的一个结点，所以target.right == null，此时preTarget.right == target，所以删除时按照上面的情况2去进行删除。

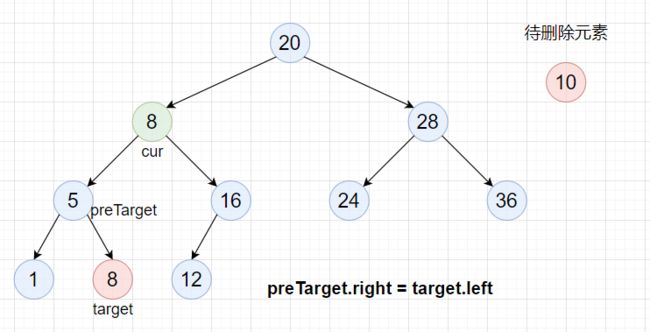
但是还有一种特殊情况，那就是cur.left就是左子树最大结点，此时preTarget==cur，即preTarget.left == target，这时删除时要将 preTarget.left = target.left。


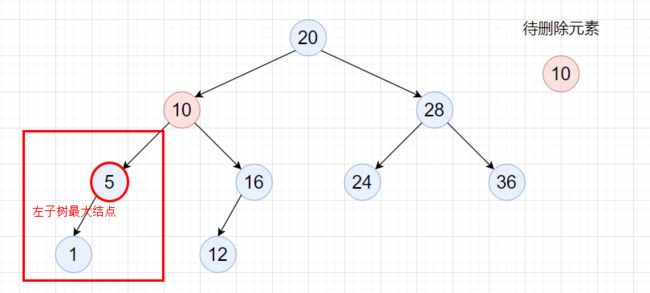
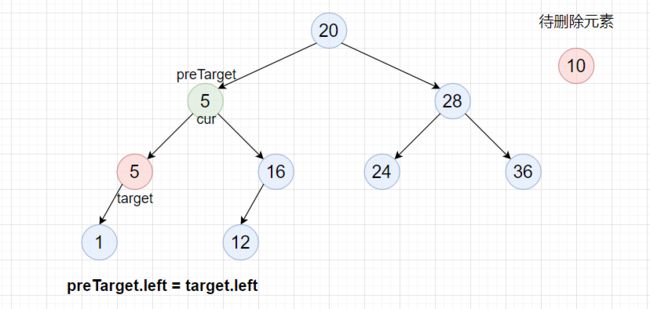
参考实现代码：

    public void remove(int key) {
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                //这里开始删除
                removeNode(cur,parent);
                break;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

removeNode方法（方案1）：

    public void removeNode(Node cur,Node parent) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node preTarget  = cur ;
            Node target  = cur.right;
            while (target.left != null) {
                preTarget = target;
                target = target.left;
            }
            cur.val = target.val;
            if (target == preTarget.left) {
                preTarget.left = target.right;
            } else {
                preTarget.right = target.right;
            }
        }
    }

removeNode方法（方案2）：

    public void removeNode(Node cur,Node parent) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node preTarget  = cur ;
            Node target  = cur.left;
            while (target.right != null) {
                preTarget = target;
                target = target.right;
            }
            cur.val = target.val;
            if (target == preTarget.left) {
                preTarget.left = target.left;
            } else {
                preTarget.right = target.left;
            }
        }
    }

2.4修改

搜索树的修改可以基于删除和插入，先删除目标元素，然后再插入修改元素。

参考实现代码：

    public void set(int key, int val) {
        remove(key);
        insert(val);
    }

3二叉搜索树的性能

在平衡二叉树的情况下（左右子树高度差不超过1），假设有n个结点，此时时间复杂度为二叉树的高度，即$O(lo{g}_{2}n)$，但是这只是例行情况，最不理想的情况就是二叉树化为单分支树，时间复杂为$O(n)$。

为了解决这个问题，后面引申出AVL树，红黑树，其中TreeMap与TreeSet的底层就是红黑树。具体红黑树是什么，这里就不多说了。

本文到底了，你学会了吗？

---

觉得文章写得不错的老铁们，点赞评论关注走一波！谢谢啦！