数的机器码表示【原码、反码、补码】笔记

前言：在本文章系列的开始，先自我介绍一下，本人计算机技术研一在读，本科通信工程。这个系列是自己写下来作为课堂笔记用的，希望在研一好好学一遍计算机的系统知识，CSDN使用方便，也可以分享出来，希望和各位一起探讨。水平有限，还请读者多多指正。

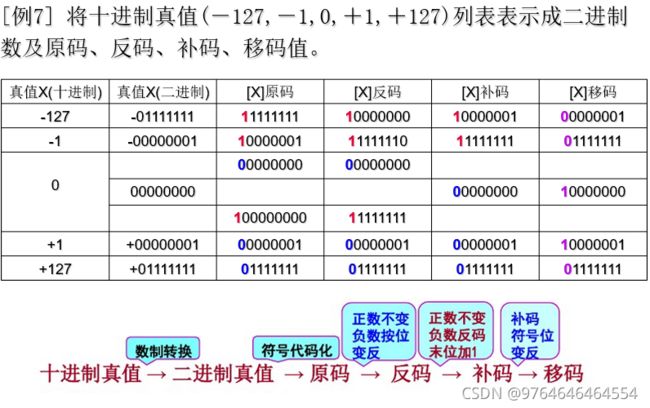
计算机使用二进制进行存储，因此衍生了一系列关于数据存储的问题，原码反码补码都是机器码，是计算机储存数据的格式，机器码是相对于真值而言，而真值可以理解为真实世界的数据。

首先
明确以下概念：
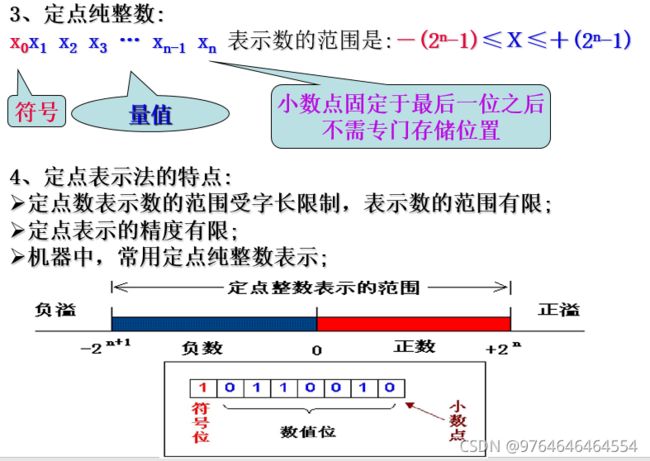
1.数的类型：整数、小数、实数、复数
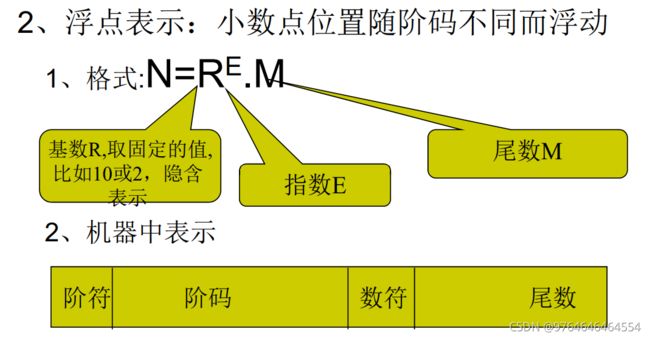
2.数据的两种表示格式：定点格式、浮点格式

图源自笔者老师PPT（下同）

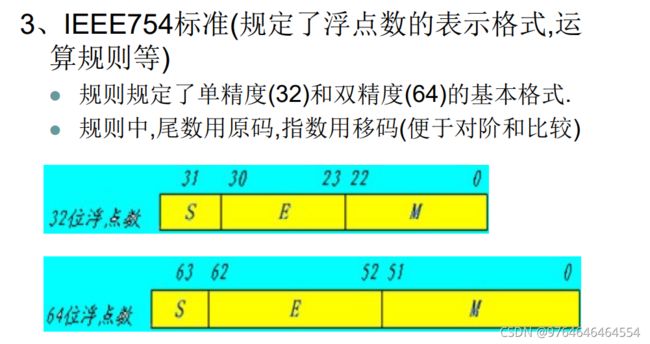
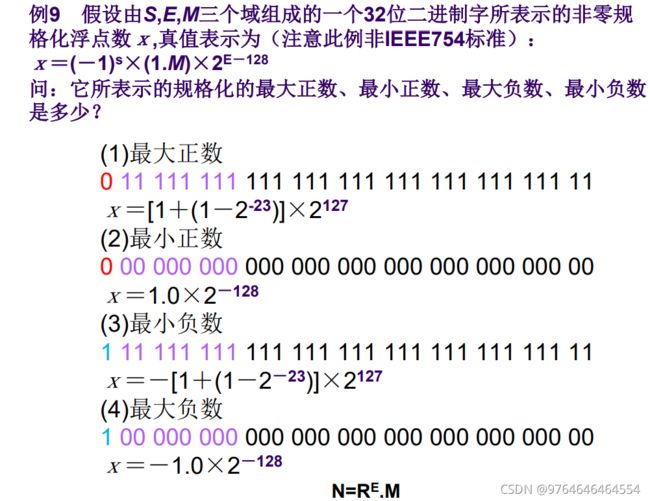
         移码的偏移值使用127，是因为省略了最高位1没有存储，实际是1.M代表整个尾数。

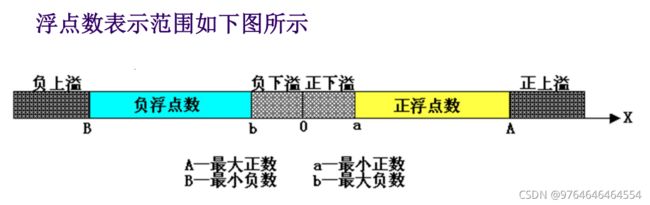
        这里顺带提一下所谓“机器零”的问题：机器“0”是指0以及0附近计算机无法表示的极小数（极小正数和极大负数，但都是0旁边的区域，即上图（b-a）。计算机将此类数默认为0.

原码      

        我们很容易将一个正数化为二进制数，无论是整数还是小数，如十进制3等于二进制11.
但如何记录负数呢？人类使用符号+-来表示正负，很容易想到机器可以使用01来表示。我们规定首位的数字表示符号，0表示+，1表示-，这样得到的原码就可以解决负数的存储问题。

        但实际存储时使用的却不是原码，而是补码，因为原码使得正负数相加的问题非常复杂，而补码使得加减操作的问题大大简化。具体可浏览：原码，反码，补码的深入理解与原理https://blog.csdn.net/afsvsv/article/details/94553228/https://blog.csdn.net/afsvsv/article/details/94553228/

反码

        正数的反码与原码相同，负数的反码即将除符号位的其余按位相反。反码有正负零如0000和1111皆表示0.

补码

        补码就是为了解决减法的问题，因为加法利于硬件实现，因此将减法转化为加法操作。利用“钟表”的思想，巧妙的解决了这一问题。具体参考上个链接，不再赘述。

模的概念可以帮助理解补数和补码。

“模”是指一个计量系统的计数范围。如时钟等。计算机也可以看成一个计量机器，它也有一个计量范围，即都存在一个“模”。例如：

时钟的计量范围是0～11，模=12。表示n位的计算机计量范围是0～2^(n)-1，模=2^(n)。

“模”实质上是计量器产生“溢出”的量，它的值在计量器上表示不出来，计量器上只能表示出模的余数。任何有模的计量器，均可化减法为加法运算。

例如：假设当前时针指向10点，而准确时间是6点，调整时间可有以下两种拨法：一种是倒拨4小时，即：10-4=6；另一种是顺拨8小时：10+8=12+6=6

在以12模的系统中，加8和减4效果是一样的，因此凡是减4运算，都可以用加8来代替。对“模”而言，8和4互为补数。实际上以12模的系统中，11和1，10和2，9和3，7和5，6和6都有这个特性。共同的特点是两者相加等于模。

对于计算机，其概念和方法完全一样。n位计算机，设n=8， 所能表示的最大数是11111111，若再加1称为100000000(9位），但因只有8位，最高位1自然丢失。又回了00000000，所以8位二进制系统的模为2^8。在这样的系统中减法问题也可以化成加法问题，只需把减数用相应的补数表示就可以了。把补数用到计算机对数的处理上，就是补码。

补码运算的优点：（1）减法运算可以用加法来实现，即用求和来代替求差。

（2）数的符号位可以同数值部分作为一个整体参与运算。

（3）两数的补码之和（差）=两数和（差）的补码

（ 1 ）参加运算操作的数都用补码表示。 （ 2 ）数据的符号与数据一样参加运算。

（ 3 ）求差时将负减数求补,用求和代替求差, 将减法运算转化为补码的加法运算。

（ 4 ）运算结果为补码。如果符号位为 0 ,表明运算结果为正；如果符号位为 1 ,则表明结果为负。

（ 5 ）符号位的进位为模值，应该去掉。 补码减法 运算公式为： [X]补–[Y]补=[X–Y]补 (3.2)

    通过 [Y]补 求得 [–Y]补 可以将减法运算转化为补码的加法运算。

    已知 [Y]补求 [–Y]补 的法则是：对 [Y]补各位（包括符号位）取反,末位加1 ，就可以得到[–Y]补

例 [Y]补 =1.1011 则 [–Y]补 =0.0101

   [Y]补 = 0.1011 则 [–Y]补 =1.0101

例 4 X=0.1100 Y=0.0110 求 [X]补–[Y]补 = ？

解: [X]补 =0·1100 [Y]补 =0·0110 [–Y]补 =1·1010

    [X]补–[Y]补 =0.0110+1.1010=0.0000

        通常利用反码来求补码，更为简单。
        补码表示数的范围扩大，如1000为4位定点整数可表示的最小值-8（即-）。

         注意补码与真值的关系公式，减去的数是模值的二分之一。如小数是1，定点整数是.

移码

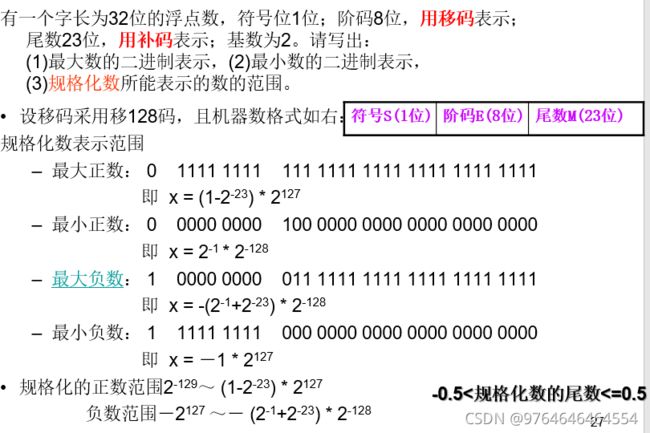
        移码与补码符号位相反，尾数相同。移码相对容易理解，4位移码，0000表示最小值-8，0001表示-7，0010表示-6，，，1000表示0，1001表示1，，，1111表示7，可见移码与补码表示范围相同，且不会出现正负0的问题。对于IEEE754中阶码的表示，移码的偏置值不同，32位为127，64位为1023.但全0时仍表示最小值，即机器0.

         上面这个例题可以帮助理解负下溢、正下溢、机器0等问题。

 

上面这个例题需要理解，补码的符号位其实就是机器数的也就是最高位的符号位，尾数23位都是补码中的尾数。之所以要求负数的最高位为0，道理和正数的最高位为1是一样的，为了规格化。

以4位定点整数为例：
原码表示最小值1111=-7，最大值0111=+7
反码表示最小值1000=-7，最大值0111=+7，1111=0
补码表示最小值1000=-8，最大值0111=+7，1111=-1
移码表示最小值0000=-8，最大值1111=+7

注：本文部分图片引自白中英版计算机组成原理。