最近在学习DIBR并尝试实现。感觉网上相关资料比较少,大多还是爬虫,决定自己写一个。
DIBR就是depth image based rendering问题。输入一个视角下的图像和深度图,要求你输出另外一个虚拟视角下的图像(当然两个视角的内外参矩阵都有办法通过已知信息求得)。
总共分三步:内参提取 和 外参提取 ,以及DIBR的主过程。这里按照网上其他博客的顺序,先介绍内参提取。看的过程中注意坐标系的定义。由于是第一次接触,这里我采用的坐标系可能和常规的坐标系不太一样。
开始之前先介绍一些定义(基于我自己实现算法的时候所使用的数据集):
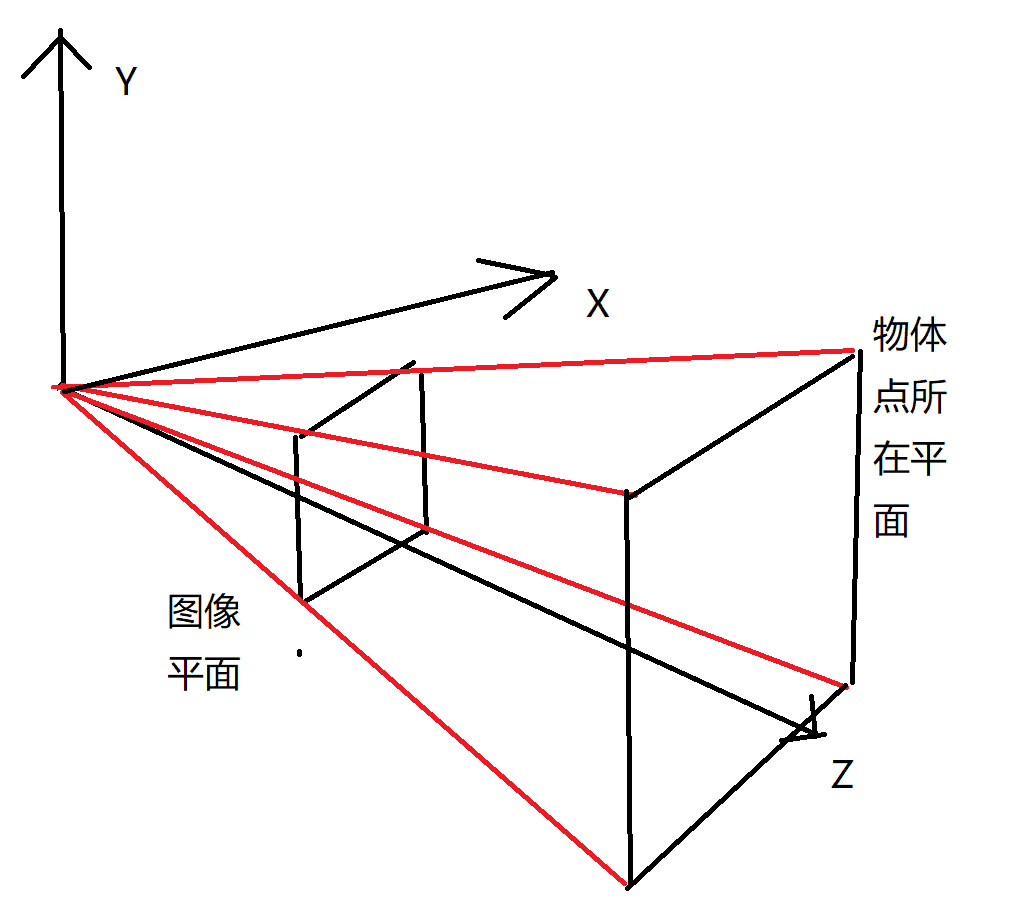
\((u,v,1)^T\)为一个点的像素坐标。
\((x,y,1)^T\)为一个点在图像平面上以物理距离衡量的坐标。
\((X,Y,Z)\)为一个点在相机坐标系下的坐标。
\((X_w,Y_w,Z_w)\)为一个点在世界坐标系下的坐标。
\(f_x、f_y\)分别表示X轴的焦距和Y轴的焦距(非理想情况下横向和纵向的焦距是不一样的)。
\(d_x、d_y\)分别表示X轴(对应于图像的U轴)和Y轴(对应于图像的V轴)每个像素的物理尺寸(一个像素实际有多长)。
\(p_u、p_v\)表示相机的主点(principal point,就是相机主轴与成像平面的交点)在图像中的位置(以像素为单位)。
像素纵横比:\(pixel\ aspect\ ratio\)。表示像素的实际尺寸的高与宽之比。
主点:\(principal\ point\)。是一个二维向量,表示相机主光轴与成像平面的交点。这里以像素为单位在图像上进行刻画。
相机位置\((position_x,position_y,position_z)\)
焦距\(focal\ length\)
相机姿态(朝向)\(camera\ orientation\)。为一个三维向量,通常可用欧拉角、轴角、四元数等方式表示。这里采用的是轴角表示法。
后面的公式可以对照着这个表来看。
内参提取
内参提取就是求从相机坐标系到最终像素图像的变换。
在看具体的矩阵之前,先看一下怎么推的。
那么就用\(\frac{y}{f}=\frac{Y}{Z}\)即\(y=\frac{fY}{Z}\)。对于x同理。
那么图像平面上的坐标(以物理长度衡量)就是\((x,y,1)=(\frac{fX}{Z},\frac{fY}{Z},1)\)。这里采用齐次坐标。表示为\((fX,fY,Z)\)。
再映射到以像素为单位的坐标系下:
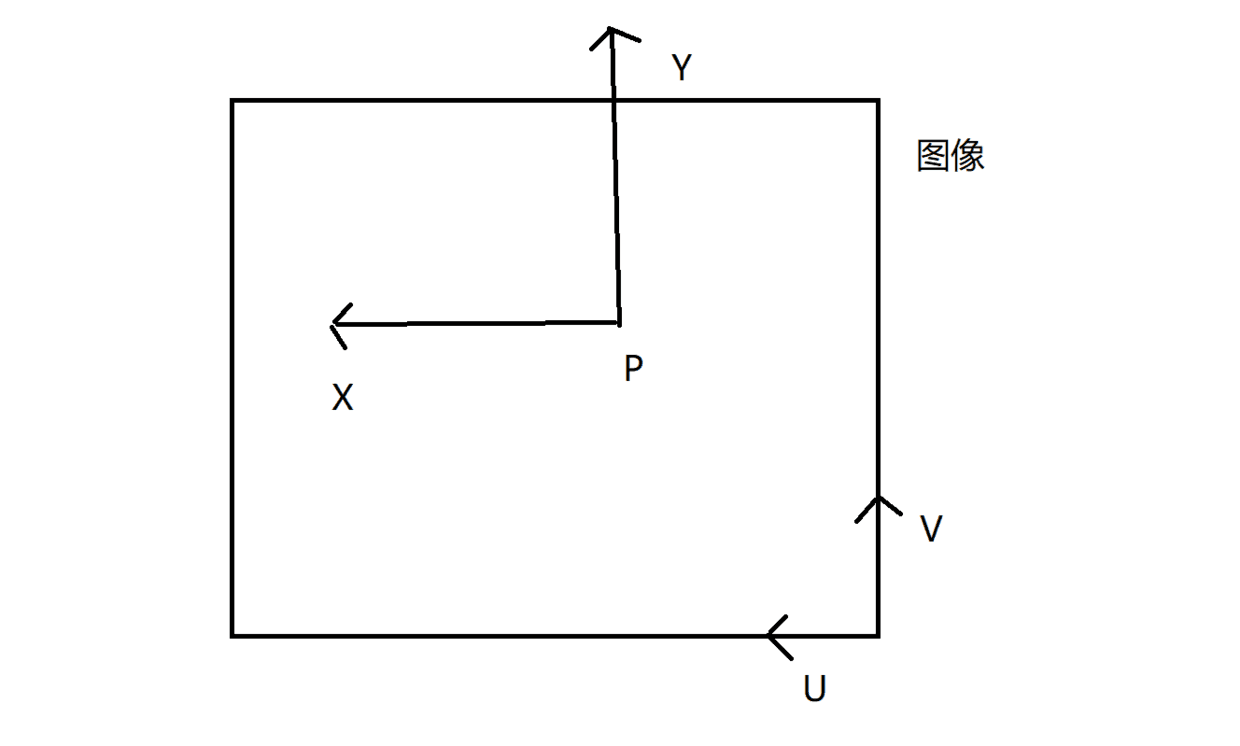
就是\(u=\frac{x}{d_x}+p_u\),v同理。那么就有\((u,v)^T=(\frac{x}{d_x}+p_u,\frac{y}{d_y}+p_v,1)\)。同样使用齐次坐标有:\((Zu,Zv,Z)=(\frac{fX}{d_x},\frac{fY}{d_y},Z)\)。后面的推理都是在齐次坐标下进行的。
接下来写出矩阵乘法的形式:
定义\(K'=\left[ \begin{matrix} f_x & 0 & 0 \\ 0 & f_y & 0 \\ 0 & 0 & 1 \end{matrix} \right]\)用于从相机坐标系转移到图像平面上的坐标系(以图片的物理尺度进行衡量,还不是像素尺度,不妨设为V坐标系)
定义\(C=\left[ \begin{matrix} \frac{1}{d_x} & 0 & p_u \\ 0 & \frac{1}{d_y} & p_v \\ 0 & 0 & 1 \end{matrix} \right]\)为从V坐标系映射到图像坐标系(以像素为尺度)
定义\(K=C*K'=\left[ \begin{matrix} \frac{f_x}{d_x} & 0 & p_u \\ 0 & \frac{f_y}{d_y} & p_v \\ 0 & 0 & 1 \end{matrix} \right]\)。 这就是我们的内参矩阵。即
其中,\(\frac{f_x}{d_x}、\frac{f_y}{d_y}\)可由定义的\(par=pixel\ aspect\ ratio\)(像素纵横比)得到。我手上的数据集给出的焦距(focal length)是以像素为单位的,应该默认是给出\(focal\ length=\frac{f_x}{d_x}\)。那么\(\frac{f_y}{d_y}=\frac{f_x}{d_x}\x par\)。也就不需要我们去计算\(d_x、d_y\)了,毕竟jpg格式的解压不是人人都会的,opencv貌似也无法直接读出图像的分辨率信息(至少我没有查到)。
外参提取
外参提取就是求从世界坐标系到相机坐标系的变换。
这里把变换拆分为旋转变换和平移向量。
先来看看平移变换,这个很好写:
相机位置是\((p_x,p_y,p_z)\)(变量名有点重复,见谅见谅),那么就有平移向量:
\(C=(-p_x,-p_y,-p_z)^T\)。\((X_w,Y_w,Z_w)^T+C\)就能够实现平移了。
接下来看旋转变换:
这里的原理还没怎么搞懂,后面再来补上,先把做法说了。
输入给的是轴角表示(axis-angle),文章给出的实现是,先转化为四元数,再用四元数进行旋转。(我的评价是,不如直接用欧拉角,这好复杂...)
首先将axis和angle转化为四元数。设axis=\((a,b,c)^T\)。得到的四元数是\(q=(a,b,c,w)^T\)。不妨设axis是单位向量。
那么有\(q=(sin(\frac{angle}{2})axis,cos(\frac{angle}{2}))^T\)。
下面用四元数得到旋转矩阵。不妨设q已经经过了单位化。
那么有:

最后就有\((X,Y,Z)^T=R((X_w,Y_w,Z_w)^T+C)\)
DIBR的核心步骤
有了两个视角下分别的内参和外参之后怎么做呢?这其实是最简单的一步。
\(Z(u,v,1)^T=KR((X_w,Y_w,Z_w)^T+C)\)
这对于两个视角下都是成立的:
\(Z_1p_1=K_1R_1(P+C_1)\)
\(Z_2p_2=K_2R_2(P+C_2)\)
用第一个式子把P求出来:
\(P=(K_1R_1)^{-1}Z_1p_1-C_1\)
再带到第二个式子里,最后把\(Z_2p_2\)弄成p2=(u,v,1)的形式就可以了。最后一步就是把p1对应的像素直接赋给p2即可。
注意:这里的Z_1,Z_2指的就是深度,所以才需要深度作为输入。这样看来,也能通过DIBR得到输出图像的深度信息。
这里写的时间不长,写的比较粗糙,如果有问题敬请指出。有时间我会回来把四元数的推导补上的。
参考:https://blog.csdn.net/u010922186/article/details/40683129