Java之TreeMap源码简单分析
TreeMap 源码简单分析
- 前言
- 一、数据结构
-
- 1、平衡二叉树（AVL树）
- 2、红黑树
- 二、添加元素
- 三、删除元素
- 总结
- 参考文献
前言
TreeMap也是TreeSet的底层，简单了解TreeMap的数据结构、添加元素、删除元素，便于更好的编程。
一、数据结构
底层一颗红黑树，加一个比较规则。
private final Comparator<? super K> comparator;
private transient Entry<K,V> root;
// Red-black mechanics
private static final boolean RED = false;
private static final boolean BLACK = true;
static final class Entry<K,V> implements Map.Entry<K,V> {
K key;
V value;
Entry<K,V> left;
Entry<K,V> right;
Entry<K,V> parent;
boolean color = BLACK;
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Returns the key.
*
* @return the key
*/
public K getKey() {
return key;
}
/**
* Returns the value associated with the key.
*
* @return the value associated with the key
*/
public V getValue() {
return value;
}
/**
* Replaces the value currently associated with the key with the given
* value.
*
* @return the value associated with the key before this method was
* called
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}
1、平衡二叉树（AVL树）
1）平衡二叉树中序遍历是一个有序的集合。
2）左右子树高度不超过1，当由于插入元素导致树失去平衡时，通过LL右单旋转、RR左单旋转、LR先左后右双旋转、RL先右后左双旋转来让二叉树达到平衡。
3）查找效率高，增加删除元素时调整平衡时开销较大。
2、红黑树
平衡二叉树适合查找多、增加删除操作少的时候，如果经常增加删除需维护平衡二叉树，所带来的开销是大于收益的。
红黑树因此诞生，一颗不严格的平衡二叉树，局部平衡整体不平衡，这样增加删除带来的开销就相对较小。
红黑树通过对节点着色（节点多出一个位置来记录颜色），没有一条路径会比其它路径长出两倍。
1 区别）旋转次数少，一颗弱平衡二叉树，适合于搜索、插入、删除操作较多的情况下。
2 特点）
- 每个节点非红即黑
- 根节点是黑的;
- 每个叶节点（叶节点即树尾端NULL指针或NULL节点）都是黑的;
- 如图所示，如果一个节点是红的，那么它的两儿子都是黑的;（从每个叶子到根的所有路径上不能有两个连续的红色结点）
- 对于任意节点而言，其到叶子点树NULL指针的每条路径都包含相同数目的黑节点;
注：这些约束强制出了红黑树的关键性质，即从根到叶子节点的最长路径不会超过最短路径的2倍，让这棵树大致是平衡的。
最短路径肯定是连续的黑节点，最长路径是红黑节点的交替（毕竟每条路上黑节点相等），而每条路径的黑节点又相等且红节点的子节点一定是黑节点，所以最长路径最多是黑节点的2倍减一。
3 树的旋转）
当我们在对红黑树进行插入和删除等操作时，对树做了修改，那么可能会违背红黑树的性质。
为了保持红黑树的性质，我们可以对相关结点做一系列的调整，通过对树进行旋转(不会改变二叉树的排序)，即修改树中某些结点的颜色及指针结构，以达到对红黑树进行插入、删除结点等操作时，红黑树依然能保持它特有的性质（五点性质）。
4）三个操作
A）查找
普通的二叉排序树查找。
B）插入
找到新节点该插入的叶节点位置，将其插入到该位置，并为其着上红色。为了保证红黑树的5个特点，需要对有关节点进行重写着色和旋转。插入节点伪代码如下：
RB-INSERT (T,z) {
1 按二叉查找树的插入步骤将结点 z 插入到 T 中；
2 color[z]=RED；
3 while(z 不是根结点 &&color[z->parent]= =RED) {Insert-Fixup(T,z);}
4 color[root[T]]=BLACK； }
注1：为什么要着红色？如果着黑色，那么就有一条路径多了一个黑色节点。此时如果新节点的父节点是黑色，那么就不做什么，如果父节点是红色，那么就需要做调整。
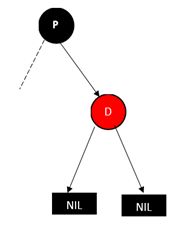
注2：三种会出现的情况（这里插入B为例）：
情况1：B的父节点A、叔叔节点D是红色的）此时将B的父节点A和叔叔节点D着色为黑色，并从祖父节点开始往上排查是否有违背红黑性质的情况。
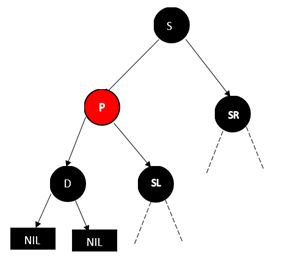
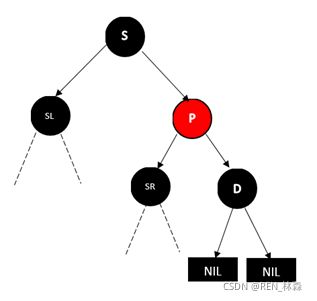
情况2：B的父节点A为红色（B插入到A的右孩子节点）A的左孩子为黑色且A的兄弟D为黑色）从B处左旋，会来到情况3，情况2、3一起处理，如下：
情况3：从B处左旋，那么原来的父节点A变成B的左孩子，现在统一处理左孩子情况）先对左孩子A的父节点着色为黑色，然后在父节点处进行一次右旋，最终使其局部满足红黑性质，以至整体满足红黑性质。转载别人的图如下：
完整插入过程：
注：旋转不超过两次，向上调整有少量O(logn)，像第二三种情况，只需要左旋、着色、右旋就解决问题了。
C）删除
二叉排序树的删除过程分为3种：
情况1：该节点是叶子节点）直接删除该节点，即把该节点父节点指向它的指针赋为null。
情况2：该节点只有一个孩子）若是左孩子，用左孩子顶替它的位置，即把它的父节点指向它的指针update成它的左孩子，再将它的左孩子指针赋值为null。右孩子同理可得（左右具有对称性）。
情况3：该节点有两个孩子）则令它的直接前驱或后继替代它的位置，然后从二叉排序树中删除这个直接前驱或后继，删除这个前驱后继又回到情况1或情况2。
红黑树的删除操作：
其操作就是建立在二叉排序树删除的基础上，来对红黑树的着色和结构进行修正，以下按删除节点的颜色来讨论：
情况1：删除红色的节点D）
- 该红色节点为叶子节点：直接删除。
- 该红色节点不是叶子节点：只可能出现被删除的节点左右子树都存在的情况，否则违背红黑树的性质。对于这种情况，我们只需要找到被删除节点的直接后继，用它的值取代被删除节点的值，然后再去删除直接后继（分这个节点是红色还是黑色）。
情况2：删除黑色节点D）
- 删除黑色叶子节点
a. 兄弟节点S为红色且D在左边
调整做法是将父亲节点和兄弟节点的颜色互换，也就是p变成红色，S变成黑色，然后将P树进行AVL树种的RR型操作。
此时，D的兄弟节点就变成了黑色，接下来统一讨论。
b. 兄弟节点S为红色且D在右边
将P和S的颜色互换，也就是将P变成红色，将S变成黑色，然后对P进行类似AVL树的LL操作。
此时，D的兄弟节点也变成了黑色，下面统一讨论。
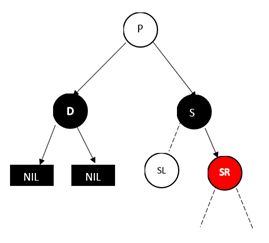
情况2：D兄弟节点为黑色，且远侄子为红色）
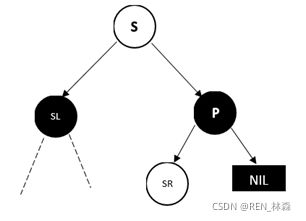
a. D在左，兄弟节点S的右孩子SR为红色
如果删除D，则该路径上黑色节点减一，但SR为红色，将其改为黑色，对换S和父节点P的颜色，再对S子树做RR左单旋即可。这也是为什么P的颜色无关，因为调整过程只在P整棵子树的内部进行。
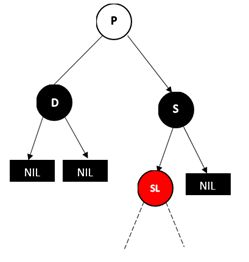
b. D 为右孩子，且兄弟节点的左孩子为红色
同样，将P和S的颜色对调，然后再对P树进行类似AVL树RL型的操作，最后将SR变成黑色，并删掉D即可。
情况3：兄弟节点为黑色，但是这次是近侄子节点为红色)刚好和情况2相反。
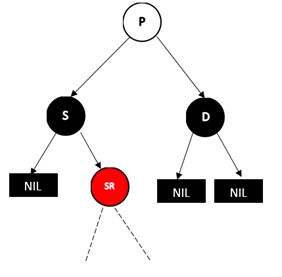
a. D 在左
将SL右旋，并将S和SL的颜色互换，则变成了情况2的a情况。
b. D为右孩子
将S和SR颜色对调，然后对SR进行左旋操作，则变成了情况2的b情况。
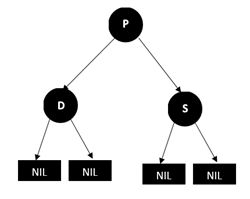
情况4：父亲节P为红色，兄弟节点和兄弟节点的两个孩子（只能是NULL节点）都为黑色的情况）
删除D，则左边路径黑色减一，则将P变为红色，但是右边路径黑色节点加1，则将右孩子节点着色为红色，若还破坏了红黑心性质，则继续向下调整。
情况5：父亲节点P，兄弟节点S和兄弟节点的两个孩子（只能为NULL节点）都为黑色的情况）
删D，左边的路径黑色减1，所以把S变为红色。但是经过P的路径上的黑色节点数会少1，这个时候，我们再以P为起始点，继续根据情况进行平衡操作（这句话的意思就是把P当成D（只是不要再删除P了），再看是那种情况，再进行对应的调整，这样一直向上，直到新的起始点为根节点）。
最后一种情况：删除黑色的非叶节点
- 删除的黑色节点左右子树都存在
首先找到被删除元素D的直接后继，用直接后继的值替换D的值，再对直接后继进行删除。我们可以知道，直接后继是不可能左右子树都存在的，这样就可以将左右子树都存在的情况转化为下面的情况2。- 删除的黑色节点仅有左子树或者仅有右子树
在红黑树中只存在下面这几种情况，单孩子的情况，那么另一个孩子必为红色节点，才满足每条路径的黑色节点相等。
这两种的处理方式是一样的，即用D的左孩子或者右孩子替换D，并DR的颜色改成黑色即可。
注：没有上色的节点表示黑色红色均可，注意如果SL为黑色，则SL必为NULL节点。
删除算法如下：
RB-DELETE(T,z) {
1 if (z 的左右子结点均为 NIL)
2 { NIL 结点代替 z 的位置； delete(z); }
3 else if (z 有一个子结点为 NIL)
4 {z 的非 NIL 子结点代替 z 的位置；delete(z); }
5 else
6 {将红黑树中序遍历中 z 的后继结点 s 的值赋给 z; delete(s); }
7 if (删除的结点是黑色的) Delete-Fixup(T,x); /*x 指向代替删除结点的结点 */ }
二、添加元素
public V put(K key, V value) {
Entry<K,V> t = root;
//树上没有节点，则root赋值，return null
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
//外部规则为空，则使用内部规则，先查找到该插入的位置
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//插入元素
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
//修正红黑树
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
三、删除元素
1、寻找要删除元素的位置
public boolean remove(Object o) {
for (Entry<K,V> e = getFirstEntry(); e != null; e = successor(e)) {
if (valEquals(e.getValue(), o)) {
//进入删除方法，分情况删除，然后调整。
deleteEntry(e);
return true;
}
}
return false;
}
2、根据情况删除
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;
// Fix replacement
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
3、删除后的修正。
/** From CLR */
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // symmetric
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
总结
1）平衡二叉树
2）红黑树，查找、插入、删除
参考文献
[1] [JDK 1.12]
[2] 红黑树与二叉平衡树的区别
[3] 红黑树百度百科
[4] 红黑树插入详解
[5] 红黑树删除详解